网络编码提高波分复用网络多源光组播带宽利用率时,导致光域中存储和运算开销增加,为此,设计了一种改进的自适应遗传算法可最少化光组播的网络编码光纤链路数目.该算法设计了自适应调整的交叉概率和差异最大化交叉操作,保证种群多样性,避免陷入局部最优;通过自适应调整交叉概率,保证种群在开始阶段可以很快实现多样性,使种群中的较优个体保持稳定.仿真结果表明,所提算法与对比算法相比收敛速度更快,可以用更短时间找到编码链路数目最少的方案.
Network coding can improve the bandwidth utilization for multi-source optical multicast, but it increases optical storage and computation overhead in wavelengeh division multi-plexing networks. An improved adaptive genetic algorithm (IAGA) is proposed to minimize the number of optical network coding links for multicast. By designing the maximization difference crossover operation, IAGA can guarantee the diversity of population and avoid from falling into a local optimal. By adaptive adjusting the crossover probability, IAGA makes the population diverse at the beginning stages and makes the excellent individuals remain in a stable condition. Compared with other algorithms, the simulation results show that the proposed algorithm has fastest convergence speed, which means that it takes the shortest time to find the minimum numbers of optical coding link solutions.
多源组播应用发展对光网络带宽提出了更大要求[1].波分复用(WDM, wavelength division multiplexing)光网络提供的波长通道数目有限[2-3],光域的网络编码还可以有效地解决WDM光网络中的波长冲突问题[3-5].但是,光域网络编码需要编码运算和消耗缓存开销[6-7].最少编码节点(MCN, minimizing coding nodes算法[7]、基于遗传算法的最小化网络编码链路算法(MCLIGA, minimizing coding links based on the improved genetic algorithm)相继提出优化编码次数[8].为了进一步减少网络编码次数和减少单源组播的带宽阻塞率,本文研究了一种改进的自适应遗传算法(IAGA)最少化光组播的网络编码光纤链路数目.
1 网络编码链路优化模型WDM网络用G(V, E, W, S, D)表示,V是节点集合,E是光链路集合,W是波长通道集合,S是源节点{s1, s2, …, sm}集合,D是目的节点集合{d1, d2, …, dn}.网络G中输入链路大于等于2的节点为潜在编码节点,设光网络中存在M个潜在编码节点,在第i个潜在编码节点上有oi条输出链路. τij是布尔变量,如果节点i上的第j条链路是编码链路,则τij为1,否则为0.光网络中编码链路的数目能够准确地反映出光网络中的编码操作次数和当前网络的编码计算开销,光组播网络中网络编码优化问题模型表示为
| $ {\rm{min}}~\sum\limits_{i=1}^{M}{\sum\limits_{j=1}^{\rm{ou}{{\rm{t}}_{\mathit{i}}}}{~{{\tau }_{{\text{ij}}}}}} $ | (1) |
约束条件:
| $ \mu (s, {{d}_{k}})=R, \forall {{d}_{k}}\in D $ | (2) |
| $ \ \ \ {{p}_{i}}(s, {{d}_{k}})\cap {{p}_{j}}(s, {{d}_{k}})=\varnothing, \\ \forall i, j\in \left\{ 1, 2, \cdots \right\}, i\ne j, \forall {{d}_{k}}\in D $ | (3) |
| $ h\le R $ | (4) |
式(1)定义了图G的最少编码链路数目问题;式(2)约束了虚拟源节点s到每个目的节点的组播速率为R;约束条件式(3)是指对于任意一个接收速率为R的目的节点dk(k=1, 2, …, n),单位容量路径集合pi(s, dk)(i=1, 2, …)中没有共享链路;约束条件式(4)是信息速率R不小于由图论“最大流-最小割”定理确定的网络组播速率上限h.
2 改进的自适应遗传算法最少多源光组播编码链路数最少网络编码链路数(式(1))问题被证明是一个NP问题[9], 遗传算法(GA, genetic algorithm)在解决此类复杂问题时具有明显的优势.笔者提出的改进的自适应遗传算法(IAGA, improved adaptive genetic algorithm)在GA基础之上通过设计组播染色体差异性最大化交叉,可以保证组播传输路径种群的多样性,避免陷入局部最优;设计自适应交叉概率保证了种群在开始阶段个体的多样性,并使种群中个体普遍较优时保证稳定性.
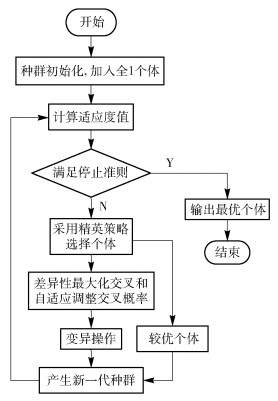
2.1 IAGAIAGA由精英策略选择、自适应调整概率的最大差异性交叉和变异3个算子构成,个体代表多源组播的一种路由方式.精英策略选择从父代个体中获取大量优秀基因,再通过自适应调整概率的最大差异性交叉重组的方式把这些优秀基因传到下一代以获得多样性的子代个体.在子代个体中还要通过适应度函数把新的优秀个体筛选出来继续传承.同时,在进化过程中,采用变异算子来引入新的基因片段. 图 1为IAGA的流程图.
|
图 1 IAGA流程图 |
在IAGA中,为了避免种群中的较优个体在参与交叉和变异时内部结构被破坏,使用精英个体保留策略把这些较优个体直接保留到下一代,并与进行交叉和变异后的染色体比较适应度值,保留适应度值更大的个体.在交叉操作中,为增加种群多样性,设计差异最大化个体交叉避免种群陷入局部最优,还设计一种根据适应度函数值的分散情况自适应地调节个体的交叉概率.
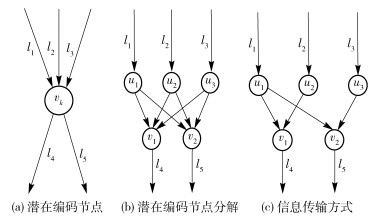
2.2 染色体构造与适应度函数的设计采用二进制编码表示链路是否传输信息,则一条染色体就表示网络中一种信息传输或路由方式.在构造染色体时,对WDM网络拓扑图先进行图分解,以化简网络拓扑[10]. 图 2是对一个潜在编码节点vk的图分解示意图.图分解是将网络拓扑中每个潜在编码节点分解成若干个辅助节点,辅助节点之间由辅助链路连接.在图 2(a)中,潜在编码节点vk有3条输入链路和2条输出链路,则将其分解为3个上游辅助节点ui(i=1, 2, 3)和2个下游辅助节点vj(j=1, 2),将ui与vj用辅助链路相连,并将潜在编码节点vk的第i条输入链路和上游辅助节点ui相连,将其第j条输出链路和下游辅助节点vj相连,最后即得到分解图如图 2(b)所示.设染色体X={w1, w2, …, wL}用一串二进制比特来表示(L是染色体X的长度),若比特位值为1,表示该基因对应辅助链路在分解图中传输信息,否则取值为0. 图 2(c)是图 2(a)中节点处的一种信息传输方式,其对应的染色体表示为“110101”,表示辅助链路u1-v1、u2-v1、u1-v2、u3-v2需要传输信息.
|
图 2 图分解示意图 |
适应度函数用于评价染色体的质量.染色体构造首先要保证其对应的路由方式能够确保信息的传输速率达到最大组播速率,当满足这个条件时就可以确定网络中编码链路的数目,编码链路的数目就设计为适应度值;如果没有达到最大组播速率,适应度值就等于原网络经节点分解后潜在编码链路数目加1.适应度函数定义为
| $ F\left( c \right)=\left\{ \begin{align} &{{n}_{c}}, \ \ \ \ \ c\ 可行 \\ &{{{{n}'}}_{c}}+1, \ \ \ \ \ \ c\ 不可行 \\ \end{align} \right. $ | (5) |
其中:c为染色体,c可行就表示其对应的路由方式能够确保信息的传输速率达到最大组播速率;nc为染色体c可行时网络中编码链路数目;n′c为原始网络节点分解后潜在编码链路数目.
2.3 自适应交叉概率为增加种群多样性,提出一种适应度值分布自适应地调节交叉概率的交叉策略.假设在父代种群中满足网络组播的最大速率的可行个体的数目为n,每个可行个体的适应度值等于网络中编码链路数目,用fi(1≤i≤n)表示,fbest表示种群中最佳个体适应度值,则交叉概率调节因子μ定义为
| $ \mu =\frac{{{f}_{\rm{best}}}}{\frac{1}{n}\sum\limits_{i=1}^{n}{f_i}} $ | (6) |
在仿真中设定的基准交叉概率是Pc′=0.8[8],在新一代种群产生中,设定交叉操作的自适应交叉概率Pc=μ×Pc′.调节因子μ∈[0, 1],当μ接近于0时,交叉概率也接近于0,这样的交叉几乎不会产生新的个体.根据仿真结果,μ∈[0.6, 1].
2.4 差异性最大化交叉在随机交叉的基础上,设计了基于个体差异性最大化的交叉操作.在交叉时,选择差异性相对较大的染色体来进行交叉.衡量差异性的标准是2条染色体基因位上的不同基因的数量.具体过程如下:
步骤1 在种群中随机选取一个上一代的染色体c,计算种群中其他染色体与c的差异性;
步骤2 选取一条与染色体c基因位相差最大的染色体;
步骤3 执行交叉操作,得到2条新一代染色体.
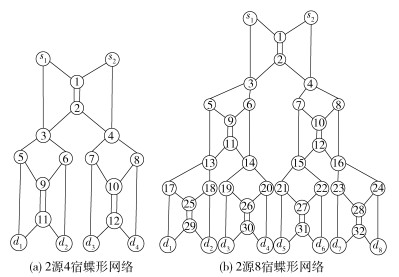
3 仿真结果及分析 3.1 仿真参数设置为了验证IAGA的性能,在不同的光网络拓扑中,使用Matlab R2012a进行仿真.对比算法分别是GA[9]、MCN算法[7]和MCLIGA[8].为了验证算法性能,分别在固定网络和随机生成网络这2种网络拓扑结构下来验证.固定的网络分别是2源4宿和2源8宿的网络,如图 3所示.
|
图 3 仿真使用的固定网络拓扑 |
随机拓扑G(20, 50, 5, 3)用Salama模型生成.设光网络中的节点均具有分光和网络编码的能力,网络中每条链路具有整数倍单位容量,多个单位容量可以看作多条并行的单位容量链路,原始网络中源节点组播率等于在单位容量链路上消耗波长数目.按图 2中分解潜在编码节点化简网络拓扑.
3种光网络拓扑结构的具体参数如表 1所示.
|
|
表 1 3种光网络拓扑结构详细参数 |
为保证公平性,将种群大小设置和对比算法一致,其他的参数还包括算法运行次数、交叉概率和迭代次数等,如表 2所示.其中,迭代次数200/500表示图 3所示固定拓扑采用200迭代终止,而随机网络采用500迭代终止.
|
|
表 2 算法中默认的参数设定 |
如表 3所示,算法GA、MCN、MCLIGA和IAGA在每个网络拓扑上运行20次,然后统计每次结果,最终算出平均结果,分别使用最少编码路由的最优值和平均编码链路数值来表征算法的有效性.可以直观看出,所提出的IAGA能获得最小的多源组播编码平均链路数和最优的编码路由方式.
|
|
表 3 算法得到的编码链路数量 |
从表 3可以看出,针对固定拓扑结构的2源4宿网络和2源8宿网络,4种算法都可以找到光组播不需要编码的路由方式,即光网络编码链路数目为0.但是,IAGA所需的平均编码路由数目最少,效果最好.在随机网络拓扑中,IAGA实现多源组播所需编码次数最少.因此,IAGA在不同网络中所需编码次数都少于其他3种算法.
表 4所示为4种算法在3种网络中搜索到组播路由最优解的运行时间.从表 4中可以看出,4种算法的运算时间随网络规模而增加.对相同网络拓扑,所提出的IAGA寻找最少网络编码次数路由所用平均时间最少,这是因为IAGA采用最大差异和自适应概率交叉,使个体以较快速度趋向最优.
|
|
表 4 算法在不同网络中每一代的运行时间 |
图 4所示为4种算法在2源4宿网络中的收敛性能.在图 4中可以发现,GA的收敛速度最慢,其他3种算法性能接近,但IAGA性能最好,能最快地找到最小编码传输路由.这是由于IAGA在交叉操作时引入了个体差异最大化交叉和自适应调节交叉概率,保证了种群较快实现多样性和种群个体普遍处于较优水平的稳定性.

|
图 4 2源4宿网络的收敛性能比较 |
在图 5中,随机网络比2源4宿网络连通度更高,路由方式更加多样,网络中潜在编码节点构成的染色体长度为79,搜索空间为279.其他3种对比算法在300代内都没有找到最优解,所提出的IAGA在179代左右就找到了最优解,表明IAGA在复杂网络中性能更好,能更快地找到最小编码链路的组播路由方式.

|
图 5 随机网络中的收敛性能比较 |
研究了在满足多源光组播网络获得最大组播速率的前提下,实现编码链路数目最少化传输路由的方法.基于GA思想提出了IAGA,通过个体适应度函数差异最大化交叉和自适应调整交叉概率的策略来快速实现种群的多样性和保证种群个体普遍较优时的稳定性.最小编码链路传输最大组播速率的多源组播信息可以有效地减少在光域的编码操作开销和光缓存需求,降低光组播交换机的代价和提高网络吞吐量,有利于促进多源组播应用的发展和提高光网络性能.
| [1] |
黄胜, 王琰, 刘焕淋, 等. 基于网络编码的多源多核点光组播路由算法[J]. 重庆邮电大学学报(自然科学版), 2014, 26(2): 143–149.
Huang Sheng, Wang Yan, Liu Huanlin, et al. Multi-source routing algorithm based on network coding in optical multicast network[J]. Journal of Chongqing University of Posts and Telecommunications(Natural Science Edition), 2014, 26(2): 143–149. doi: 10.3979/j.issn.1673-825X.2014.02.001 |
| [2] | Zhou Hui, Mao Shiwen, AGRAWAL P. Optical power allocation for adaptive transmissions in wavelength-division multiplexing free space optical networks[J]. Digital Communications and Networks, 2015, 1(3): 171–180. doi: 10.1016/j.dcan.2015.09.001 |
| [3] |
陈勇, 籍慧琴, 刘焕淋, 等. 透明IP Over WDM网络中一种能效链路控制策略[J]. 北京邮电大学学报, 2015, 38(6): 41–46.
Chen Yong, Ji Huiqin, Liu Huanlin, et al. An energy-efficiency link control strategy for transparent IP over WDM networks[J]. Journal of Beijing University of Posts and Telecommunications, 2015, 38(6): 41–46. |
| [4] | Qu Zhijian, Zhang Xianwei, Shi Shaojian, et al. Network coding based all-optical multicast in WDM networks[J]. Journal of China Universities of Posts and Telecommunications, 2015, 22(1): 89–94. doi: 10.1016/S1005-8885(15)60630-6 |
| [5] | Halloush R, Liu Hang, Dong Lijun, et al. Hop-by-hop content distribution with network coding in multihop wireless networks[J]. Digital Communications and Networks, 2017, 3(1): 47–54. doi: 10.1016/j.dcan.2016.08.001 |
| [6] | Xing Huanlai, Qu Rong, Bao Lin, et al. On minimizing coding operations in network coding based multicast:an evolutionary algorithm[J]. Applied Intelligence, 2014, 41(3): 820–836. doi: 10.1007/s10489-014-0559-4 |
| [7] |
郝琨, 金志刚. 一种最小化编码节点的网络编码优化算法[J]. 电子与信息学报, 2011, 33(2): 260–265.
Hao Kun, Jin Zhigang. An optimization algorithm of network coding for minimizing coding nodes[J]. Journal of Electronics & Information Technology, 2011, 33(2): 260–265. |
| [8] |
邵星, 王汝传, 黄海平, 等. 基于模拟退火遗传算法的网络编码优化研究[J]. 南京邮电大学学报(自然科学版), 2013, 23(2): 80–85.
Shao Xing, Wang Ruchuan, Huang Haiping, et al. Research of network coding optimization based on simulated annealing genetic algorithm[J]. Journal of Nanjing University of Posts and Telecommunications(Natural Science Edition), 2013, 23(2): 80–85. |
| [9] | Xing Huanlai, Qu Rong. A compact genetic algorithm for the network coding based resource minimization problem[J]. Applied Intelligence, 2012, 36(4): 809–823. doi: 10.1007/s10489-011-0298-8 |
| [10] |
刘焕淋, 秦亮, 向劲松, 等. 图压缩优化光组播最小网络编码路由[J]. 光电子·激光, 2013, 24(8): 1472–1476.
Liu Huanlin, Qin Liang, Xiang Jinsong, et al. An optimization algorithm of network coding for minimizing coding nodes[J]. Journal of Electronics & Information Technology, 2013, 24(8): 1472–1476. |


