2. 中国科学院大学, 北京 100190
2. University of Chinese Academy of Sciences, Beijing 100190, China
The data from the motion measuring system is the basis to estimate the motion errors in synthetic aperture sonar. By taking advantage of the centralized Kalman filter, the optimal estimation can be realized after multisensor data fusion, which is more accurate than any raw data. The experiment results show that motion compensation with multisensor data fused can make the image radiation performance improved, energy centralized and the target focused well.
合成孔径声纳利用小孔径基阵随平台在方位向做匀速直线运动,发射声波并接收回波,对合成虚拟大孔径内的回波数据进行相干处理,从而实现对观测区域的高分辨率成像.与实孔径不同,合成孔径利用小孔径运动形成虚拟大孔径,运动状态不理想将会导致波束形成时达不到理想分辨率,且距离向越远的区域合成孔径越长,成像质量越容易受到影响.合成孔径声纳在水中不可避免会受到海流、风浪影响而偏离理想航线,为了获得高质量的图像,需要对合成孔径声纳进行运动误差估计和补偿[1].
合成孔径声纳运动补偿大致分为3种方式[2]:第1种是基于运动测量系统[3-7];第2种是基于回波相关性[8-9];第3种是基于图像域自聚焦[10].运动测量系统输出数据精度有限但相对准确,数据率高,鲁棒性好,通常作为估计运动误差的首要依据.单纯使用回波相关性估计误差时,如果声纳运动误差较大,会造成回波相关性下降而导致方法失效,因此需要结合运动测量系统一同估计运动误差,可提高估计准确性.图像域自聚焦则是在前2种方法的基础上修正残余误差.因此,基于运动测量系统的运动误差估计方法在合成孔径声纳运动补偿中起着非常重要的作用.朱沛胜等[3]引入M估计方法进行参数最优估计,主要解决了运动测量系统的观测野值对声纳运动估计的影响.殷海庭等[4]提出了基于实际航迹的合成孔径声纳成像算法,利用惯性测量系统获得声纳工作过程中的实际位置,并在实际位置进行逐点波束形成,物理意义明确,模型简单,但惯性测量系统输出位置数据容易发散,造成补偿不准确. Hagen等[5]研究了水下无人平台合成孔径声纳成像问题,水下自主航行器配备有多种运动传感器,后处理时对回波加入运动状态信息,可较大提高成像质量.李厚全等[6]提出了将罗经输出的姿态数据传给多普勒声速剖面仪,利用无损卡尔曼滤波估计运动参数,可提高运动误差估计精度,为运动补偿提供了支持.张远彪等[7]研究了非“停—走—停”模式下多子阵合成孔径声纳空间运动误差模型,利用运动测量设备获得发射阵元与接收阵元运动偏差,结合距离多普勒成像算法对回波相位补偿,提高了成像质量,但未对运动误差估计方法进行说明.
合成孔径声纳运动测量系统通常包括惯性导航系统(INS, inertial navigation system)、全球定位系统(GPS, global positioning system)和多普勒测速仪(DVL, Doppler velocity logs). 3种传感器设备各有特色且优缺点并存,采用集中卡尔曼滤波技术对3类传感器数据进行融合获取最优的姿态、运动估计值,得到单个设备所不能达到的定位或测速的精度,然后在成像算法中补偿实际位置与假定理想位置之间的偏差,最终获得高分辨率的图像.
1 合成孔径声纳运动测量系统合成孔径声纳运动误差包括3维空间6自由度的运动误差,主要体现在3方面:①方位向加速度不为零,造成纵荡误差;②距离向与高度向速度不为零,分别造成横荡误差和升沉误差;③存在绕3个坐标轴的横滚、偏航和俯仰运动,这些运动误差会改变波束指向或回波声程,从而影响图像信噪比和对比度.其中纵荡误差影响较小,主要考虑横荡误差和升沉误差对成像结果的影响.惯导系统可以给出比较全面的合成孔径声纳运动状态信息,GPS输出位置信息,DVL提供位置、速度信息,接着利用集中卡尔曼滤波方法集中处理传感器数据.运动测量系统结构图如图 1所示,集中卡尔曼滤波状态变量为INS导航参数误差状态和其他导航系统误差状态的组合,输出的误差估计量可用来对导航系统进行校准.

|
图 1 运动测量系统结构 |
导航系统的误差方程是非线性方程,由于具有一定精度导航系统的误差量可看作小量,非线性方程中关于误差量的高阶项可看作高阶小量可忽略不计,所以误差方程可描述为线性方程.量测量为2种非相似导航系统对同一导航参数输出量的差值,也具有线性形式.因此对于多传感器组成的运动测量系统,采用集中卡尔曼滤波进行数据融合.
2.1 建立状态方程使用完全状态法建立状态方程.由INS误差模型可确定INS状态方程为
| $ {{{\mathit{\boldsymbol{\dot{X}}}}}_{\rm{INS}}}={{\mathit{\boldsymbol{F}}}_{\rm{INS}}}{{\mathit{\boldsymbol{X}}}_{\rm{INS}}}+{{\mathit{\boldsymbol{w}}}_{\rm{INS}}} $ | (1) |
其中:FINS为18×18系数矩阵,元素值由状态变量误差模型[11]给出;wINS为18维INS系统噪声,是高斯白噪声;INS的状态变量XINS共18维,即
| $ \begin{align} &{{\mathit{\boldsymbol{X}}}_{\rm{INS}}}=[\delta {{v}_{\rm{eI}}}\delta {{v}_{\rm{nI}}}\delta {{v}_{\rm{uI}}}\delta {{\lambda }_{\rm{I}}}\delta {{L}_{\rm{I}}}\delta {{h}_{\rm{I}}}{{\phi }_{\rm{e}}}{{\phi }_{\rm{n}}}{{\phi }_{\rm{u}}} \\ &\ \ \ \ \ \ {{\varepsilon }_{\rm{be}}}{{\varepsilon }_{\rm{bn}}}{{\varepsilon }_{\rm{bu}}}{{\varepsilon }_{\rm{re}}}{{\varepsilon }_{\rm{rn}}}{{\varepsilon }_{\rm{ru}}}{{\mathit{\nabla} }_{\rm{e}}}{{\mathit{\nabla} }_{\rm{n}}}{{\mathit{\nabla} }_{\rm{u}}}{{]}^{\rm{T}}} \\ \end{align} $ | (2) |
其中:δveI、δvnI、δvuI分别为东北天3方向速度误差,δλI、δLI、δhI分别为经纬高度位置误差,ϕe、ϕn、ϕu分别为东北天3方向平台角误差,εbe、εbn、εbu为陀螺仪随机常值漂移,εre、εrn、εru为相关漂移,∇e、∇n、∇u为加速度零偏.
GPS的状态方程为
| $\mathit{\boldsymbol{\dot{X}}}{{~}_{\rm{GPS}}}={{\mathit{\boldsymbol{F}}}_{\rm{GPS}}}{{\mathit{\boldsymbol{X}}}_{\rm{GPS}}}+{{\mathit{\boldsymbol{w}}}_{\rm{GPS}}} $ | (3) |
其中:FGPS为3×3系数矩阵[11];wGPS为3维GPS系统噪声,是高斯白噪声;GPS状态变量XGPS共3维,为
| $ \mathit{\boldsymbol{X}}{{~}_{\rm{GPS}}}={{[\delta {{\lambda }_{\rm{G}}}\delta {{L}_{\rm{G}}}\delta {{h}_{\rm{G}}}]}^{\rm{T}}} $ | (4) |
其中δλG、δLG、δhG分别为GPS经纬高度位置误差.
DVL状态方程为
| $ \mathit{\boldsymbol{\dot{X}}}{{~}_{\rm{DVL}}}={{\mathit{\boldsymbol{F}}}_{\rm{DVL}}}{{\mathit{\boldsymbol{X}}}_{\rm{DVL}}}+{{\mathit{\boldsymbol{w}}}_{\rm{DVL}}} $ | (5) |
其中:FDVL为6×6系数矩阵[11];wDVL为6维DVL系统噪声,是高斯白噪声;DVL状态变量XDVL共6维,为
| $ \mathit{\boldsymbol{X}}{{~}_{\rm{DVL}}}={{[\delta {{v}_{\rm{eD}}}\delta {{v}_{\rm{nD}}}\delta {{v}_{\rm{uD}}}\delta {{\lambda }_{\rm{D}}}\delta {{L}_{\rm{D}}}\delta {{h}_{\rm{D}}}]}^{\rm{T}}} $ | (6) |
其中:δveD、δvnD、δvuD分别为DVL东北天3方向速度误差,δλD、δLD、δhD分别为DVL经纬高度位置误差.
因此,集中卡尔曼滤波状态方程可以表示为
| $ \mathit{\boldsymbol{\dot{X}}}=\left[\begin{matrix} {{\mathit{\boldsymbol{F}}}_{\rm{INS}}}&{}&{} \\ {}&{{\mathit{\boldsymbol{F}}}_{\rm{GPS}}}&{} \\ {}&{}&{{\mathit{\boldsymbol{F}}}_{\rm{DVL}}} \\ \end{matrix} \right]\left[\begin{matrix} {{\mathit{\boldsymbol{X}}}_{\rm{INS}}} \\ {{\mathit{\boldsymbol{X}}}_{\rm{GPS}}} \\ {{\mathit{\boldsymbol{X}}}_{\rm{DVL}}} \\ \end{matrix} \right]+\left[\begin{matrix} {{\mathit{\boldsymbol{w}}}_{\rm{INS}}} \\ {{\mathit{\boldsymbol{w}}}_{\rm{GPS}}} \\ {{\mathit{\boldsymbol{w}}}_{\rm{DVL}}} \\ \end{matrix} \right]~ $ | (7) |
将运动测量系统形成的所有量测值作为集中滤波器的量测量,使用局部观测法建立量测方程为
| $ \mathit{\boldsymbol{Z}}=\left[\begin{matrix} {{\mathit{\boldsymbol{H}}}_{I1}} &-{{\mathit{\boldsymbol{H}}}_{\rm{G}}}&0 \\ {{\mathit{\boldsymbol{H}}}_{I2}}&0 &-{{\mathit{\boldsymbol{H}}}_{\rm{D}}} \\ \end{matrix} \right]\left[\begin{matrix} {{\mathit{\boldsymbol{X}}}_{\rm{INS}}} \\ {{\mathit{\boldsymbol{X}}}_{\rm{GPS}}} \\ {{\mathit{\boldsymbol{X}}}_{\rm{DVL}}} \\ \end{matrix} \right]+\left[\begin{matrix}\rm{ }{{\mathit{\boldsymbol{V}}}_{\rm{G}}}\\{{\mathit{\boldsymbol{V}}}_{\rm{D}}}\\ \end{matrix} \right] $ | (8) |
其中:HI1=[03×3 I3×3 03×12], HG=I3×3, HI2=[I6×606×12], HD=I6×6为量测矩阵,VG、VD分别为GPS和DVL量测噪声.
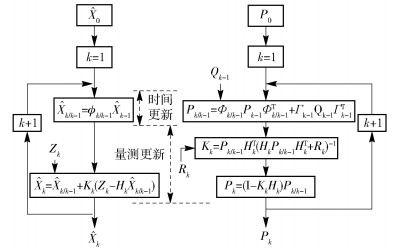
2.3 时间更新和量测更新卡尔曼滤波依据最小均方误差准则,用状态方程和量测方程描述系统特性,对系统状态矢量进行递推估计.如图 2所示,在一个滤波周期内,卡尔曼滤波具有2个明显的信息更新过程:时间更新和量测更新,分别体现了状态预测和估值修正的思想[12]. Φk, k-1为状态转移矩阵,Qk为系统噪声方差阵,Γk为系统噪声驱动阵,Rk为量测噪声方差阵,
|
图 2 卡尔曼滤波计算过程 |
拖船通过拖缆连接着拖体在水中航行,拖体内装有合成孔径声纳发射和接收设备,INS和DVL等运动测量设备负责记录拖体位置、速度和姿态等信息,GPS在干端辅助定位.利用集中卡尔曼滤波对传感器数据处理后得到位置和速度的估计误差,由此计算阵元相位中心的实际位置与理想位置之间的偏差,由声程差转换成相位差对回波数据进行补偿,最终利用成像算法生成图像.
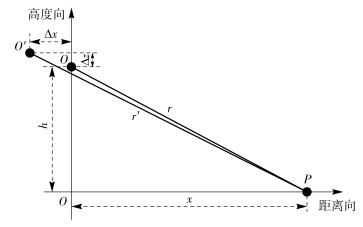
图 3是包含横荡误差和升沉误差的成像几何端射图,设垂直纸面方向为声纳前进方向,某时刻声纳在理想航迹下位于O处,存在横荡误差和升沉误差的情况下,测得声纳位于O′处.声纳与目标P距离向相距x,高度相差h.
|
图 3 存在横荡误差和升沉误差时的成像几何端射图 |
目标与声纳理想斜距为
| $ r=\sqrt{{{x}^{2}}+{{h}^{2}}} $ | (9) |
而实际斜距为
| $ {r}'=\sqrt{{{(x+\Delta x)}^{2}}+{{(h+\Delta z)}^{2}}} $ | (10) |
对斜距偏差做近似处理为
| $ \Delta r={r}'-r\approx \frac{x}{\sqrt{{{x}^{2}}+{{h}^{2}}}}\Delta x+\frac{h}{\sqrt{{{x}^{2}}+{{h}^{2}}}}\Delta z $ | (11) |
将斜距偏差换算成相位误差对回波进行补偿,f代表信号频率,c代表水中的声速,则相位误差表达式为
| $ \Delta \phi =2{\rm{ \mathsf{ π}}}{\mathit{f}}\frac{2\Delta r}{c}=\frac{4\mathsf{ π}f}{c}\left( \frac{\Delta x\sqrt{{{r}^{2}}-{{h}^{2}}}}{r}+\frac{\Delta zh}{r} \right) $ | (12) |
为验证基于多传感器数据融合的运动补偿算法的有效性,在理想航迹上引入随机横荡误差与升沉误差,针对点目标进行仿真实验. INS、GPS、DVL三类传感器对声纳实际运动状态进行测量,根据状态方程和量测方程得到传感器量测值.由于传感器自身系统特性的不同和量测误差的存在,传感器量测值各不相同.将各传感器量测值输入卡尔曼滤波器,经过数据融合后得到横荡误差和升沉误差,如图 4所示.为便于对比,引入INS、GPS和DVL经滤波后输出的位置误差与融合算法进行比较.可以发现,融合算法和GPS、DVL几乎同时开始收敛,INS收敛稍慢.随着时间的推进,融合算法相比于单一传感器估计位置误差收敛值更小,说明融合算法综合利用了各个传感器数据,达到了比单一传感器更精确的估计值.

|
图 4 横荡误差和升沉误差估计结果 |
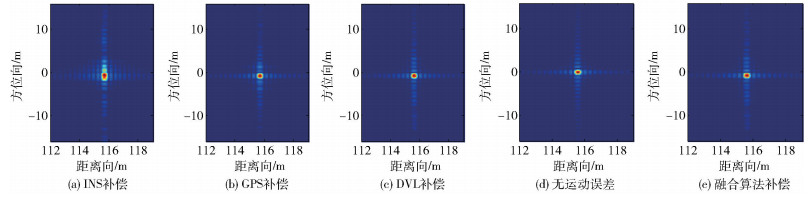
图 5为不存在横荡误差和升沉误差情况下的点目标成像图(见图(d)),以及存在横荡误差和升沉误差的情况下,按照式(12)对回波进行单传感器补偿与多传感器数据融合补偿后的点目标成像图(见图(a)(b)(c)(e)).从图 5中可以看出,INS补偿的点目标散焦情况较为严重,尤其是方位向能量不集中;GPS和DVL补偿的点目标方位向主瓣能量集中,但副瓣粗糙.由于INS获得位置误差是通过加速度二次积分而来的,所以会引入较大偏差.相比之下,多传感器数据融合后的点目标聚焦效果更好.
|
图 5 点目标成像结果 |
引入辐射性能指标[13]对点目标成像质量进行客观评价,峰值旁瓣比计算公式为RPSLR=20lg
|
|
表 1 辐射性能指标 |
为了提高合成孔径声纳成像质量,需对回波数据进行运动补偿,实验数据表明,基于多传感器数据融合的集中卡尔曼滤波方法可有效提高运动误差估计精度,进而提高运动补偿准确性.对图像辐射性能指标进行分析得出,目标峰值旁瓣比和积分旁瓣比均有改善,尤其方位向指标改善较大,说明经过数据融合后可降低运动估计误差,补偿后目标能量更加集中,聚焦良好.
| [1] | Gough P T, Hawkins D W. Imaging algorithms for a strip-map synthetic aperture sonar:minimizing the effects of aperture errors and aperture undersampling[J]. IEEE Journal of Oceanic Engineering, 1997, 22(1): 27–39. doi: 10.1109/48.557537 |
| [2] | Hayes M P, Gough P T. Synthetic aperture sonar:a review of current status[J]. IEEE Journal of Oceanic Engineering, 2009, 34(3): 207–224. doi: 10.1109/JOE.2009.2020853 |
| [3] |
朱沛胜, 黄勇, 张春华. 合成孔径声纳运动估计的鲁棒Kalman滤波方法[J]. 西安电子科技大学学报(自然科学版), 2007, 34(3): 490–494.
Zhu Peisheng, Huang Yong, Zhang Chunhua. Synthetic aperture sonar movement estimation using the robust Kalman filter[J]. Journal of Xidian University (Natural Science Edition), 2007, 34(3): 490–494. |
| [4] |
殷海庭, 刘纪元, 张春华. 基于惯性测量系统的合成孔径声呐运动补偿[J]. 电子与信息学报, 2007, 29(1): 63–66.
Yin Haiting, Liu Jiyuan, Zhang Chunhua. Motion compensation of synthetic aperture sonar based on inertial measuring system[J]. Journal of Electronics & Information Technology, 2007, 29(1): 63–66. |
| [5] | Hagen P E, Hansen R E. Robust synthetic aperture sonar operation for AUVs[C]//OCEANS 2009. Biloxi, MS, USA:[s.n.], 2009:1-6. |
| [6] |
李厚全, 赵海彬, 李伟刚, 等. 基于UKF滤波的SAS水下导航方法[J]. 武汉理工大学学报, 2010, 34(1): 97–100.
Li Houquan, Zhao Haibin, Li Weigang, et al. Navigation of synthetic aperture sonar(SAS) under water based on UKF[J]. Journal of Wuhan University of Technology, 2010, 34(1): 97–100. |
| [7] |
张远彪, 朱三文. 多子阵合成孔径声纳空变运动补偿[J]. 计算机应用, 2014, 34(S): 352–355.
Zhang Yuanbiao, Zhu Sanwen. Space-variant motion compensation for multi-element synthetic aperture sonar[J]. Journal of Computer Application, 2014, 34(S): 352–355. |
| [8] | Bellettini A, Pinto M A. Theoretical accuracy of synthetic aperture sonar micronavigation using a displaced phase-center antenna[J]. IEEE Journal of Oceanic Engineering, 2002, 27(4): 780–789. doi: 10.1109/JOE.2002.805096 |
| [9] |
江泽林, 刘维, 李保利, 等. 一种基于分段DPC和拟合的合成孔径声呐运动补偿方法[J]. 电子与信息学报, 2013, 35(5): 1185–1189.
Jiang Zelin, Liu Wei, Li Baoli, et al. A motion compensation method for synthetic aperture sonar based on segment displaced phases center algorithm and errors fitting[J]. Journal of Electronics and Information Technology, 2013, 35(5): 1185–1189. |
| [10] | Fortune S A, Hayes M P, Gough P T. Statistical autofocus of synthetic aperture sonar images using image contrast optimization[C]//OCEANS 2001. Honolulu, HI:[s.n.], 2001:163-169. |
| [11] | 秦永元, 张洪钺, 汪叔华. 卡尔曼滤波与组合导航原理[M]. 西安: 西北工业大学出版社, 2015: 362-377. |
| [12] | Simon Haykin. Adaptive filter theory[M]. McMaster University: Communications Research Laboratory, 2001: 369-397. |
| [13] |
王建国, 邱会中, 黄顺吉. 合成孔径雷达图像质量的评估指标[J]. 电子科技大学学报, 1992, 21(5): 485–490.
Wang Jianguo, Qiu Huizhong, Huang Shunji. The evaluating parameter system of the synthetic aperture radar images[J]. Journal of University of Electronic Science and Technology of China, 1992, 21(5): 485–490. |


