如何度量测试用例集合的检错能力是软件测试的核心问题之一.变异测试技术^[1-3]被研究者提出，用于衡量测试用例集合的检错能力.变异测试使用变异算子对被测试语句产生语法变异，将生成的变异缺陷作为现实世界软件缺陷的代表^[4-5]，利用变异评分评价测试用例集合的充分性^[6-7].此外变异测试的研究者也开发出一些变异测试工具^[8-9].

AJ Offutt等^[10]指出测试用例集合的变异评分与被播种的软件缺陷的检测难度密切相关. 因此在检测难度未知的缺陷集上计算出的变异评分受到质疑.

在提出的缺陷失效模型中，将软件缺陷被识别出的概率看成以下3个概率的乘积：执行到一个软件缺陷的概率(执行概率)，产生一个不正确的数据状态的概率(传染概率)，把这个不正确的数据状态传播给输出的概率(传播概率)^[11]. Voas等^[12]还提出利用动态分析方法，在被测试程序的输入域内以均匀随机的方式产生测试用例，利用这些随机测试用例的执行结果来估计缺陷的检测难度.

为了度量基于代码覆盖的测试用例集合的检错能力，Chen^[13]等研究者提出了表达式的缺陷暴露率.表达式的缺陷暴露率被定义为在程序的输入域内，以随机的方式产生并且能够执行到该表达式的所有测试用例里，能够识别出此表达式内存在的缺陷的测试用例的比例.

虽然变异评分和各种缺陷检测难度被分别研究过，但至今研究者还没有给出一个函数，使之刻画缺陷的识别概率随缺陷检测难度的变化所呈现出的规律.

于是笔者提出了一种评价测试用例集合的充分性的方法.此法借助回归模型建立缺陷的识别概率与缺陷的检测难度之间的函数关系.首先基于路径输入域生成均匀分布的随机测试用例并将其执行，以此计算缺陷检测难度.然后执行待评估的测试用集合，记录缺陷检测结果.最后以缺陷的检测难度和检测结果做数据样本，借助logistic回归建立缺陷的识别概率与缺陷检测难度之间的数量关系.这种数量关系以曲线形式表达，反映了测试用例集合的检错能力.借助关系曲线之下的面积，每一个表达式被检测的充分性被定义.此充分性被称为表达式的变异评分.基于表达式的变异评分，被测试函数的变异评分被重新定义.它是被测试程序中所有表达式的变异评分的平均值.

1 建模测试用例集合的检错能力的基本思路

测试用例集合的检错能力模型的建模过程由两大部分组成，第1部分是缺陷检测数据的获取，第2部分是建立与拟合检错能力模型.

1.1 缺陷检测数据的获取

提出了一种软件缺陷检测数据的获取方案.方案涉及2个方面：第1方面是缺陷的检测难度的计算，第2方面是从缺陷的检测结果中提取有效数据.

1) 缺陷的检测难度的计算

缺陷检测难度的计算过程如下：首先以不可重复的随机抽样方式在被测试函数的控制流程图中选中一部分表达式e_i，i=1，2，…，I.将这些表达式构成的样本集合记为S.接着以集合S中的每一个表达式e_i为目标，在控制流程图上以可重复的随机方式进行h条完整路径的选择，并在每一条选中的路径内以均匀随机的方式生成1个测试用例.此测试用例称为以表达式e_i为目标的均匀随机测试用例.在集合S的每一个表达式e_i上，以随机的方式播种n_i个缺陷m_ij，i=1，2，…，I，j=1，2，…，n_i.最后把以表达式e_i为目标的所有均匀随机测试用例中能够识别缺陷m_ij的测试用例的比例x_ij称为软件缺陷m_ij的暴露概率.缺陷的暴露概率越大表明缺陷的检测难度越低.

在上述过程中，生成均匀分布的测试用例的具体方法如下.首先将路径约束分解为多个不含否定的简单合取范式的析取结构.然后随机选择一个合取范式作为路径约束条件的代表.当路径代表约束只包含一次算数表达式时，路径代表约束表现为一个凸多面体.此时调用R语言开源软件包hitandrun.开源软件hitandrun利用马尔可夫蒙特卡洛方法在线性约束构成的凸多面体内实现了均匀随机抽样^[14-15].随后将均匀随机抽样的数据封装成测试用例.在利用开源软件进行均匀随机抽样之前，要在路径代表约束中添加测试用例的取值上界与下界，以防止生成的测试用例在执行过程中发生溢出.

2) 缺陷检测结果的提取

将待评估的测试用例集合T中的测试用例按照生成的先后顺序在软件缺陷m_ij上执行.如果缺陷m_ij不能被在其上执行的前k-1个测试用例识别的条件下，依然不被第k个测试用例识别，那么记检测结果y_ijk=1，否则记y_ijk=0.称此种缺陷检测结果被称为基于条件的缺陷检测结果.当缺陷m_ij被执行在其上的第L个测试用例首次检测到时，利用缺陷m_ij获得的基于条件的缺陷检测结果总数h_ij等于L，否则缺陷m_ij不能被测试用例集合检测到，h_ij等于在缺陷m_ij上执行过的测试用例个数l_i.此方法使得S上一共产生

$ \left| S \right| = \sum\limits_{i = 1}^I {\sum\limits_{j = 1}^{{n_i}} {{h_{ij}}} } $

(1)

个基于条件的缺陷检测结果.

将具有暴露概率为x_ij的缺陷m_ij不被在其上执行的前k-1个测试用例识别的条件下，不能被第k个测试用例识别的概率简称为缺陷m_ij的第k个不能被识别的条件概率，记为q_ij(x_ij，k).

1.2 测试用例集合的检错能力模型的构建与拟合策略

使用条件概率对测试用例集合的检错能力进行建模的原理如下.

暴露概率为x_ij的缺陷m_ij不能被识别的概率

$ {q_{ij}}\left( {{x_{ij}}} \right) = \prod\limits_{k = 1}^{{l_i}} {{q_{ij}}\left( {{x_{ij}},k} \right)} $

(2)

其中q_ij(x_ij，1)被定义为缺陷m_ij被第1个测试用例执行时不能被识别的概率.为了便于分析，假定缺陷不能被识别的条件概率只由缺陷的检测难度x和执行在该缺陷上的测试用例序号k决定.假定表达式e_i被l_i个测试用例执行过，则可以使用函数曲线q(x)下的面积与单位1的差距

$ \begin{array}{*{20}{c}} {{p_i} = 1 - \int_{x = 0}^1 {q\left( x \right){\rm{d}}x} = }\\ {1 - \int_{x = 0}^1 {\prod\limits_{k = 1}^{{l_i}} {{q_{ij}}\left( {x,k} \right){\rm{d}}x} } } \end{array} $

(3)

代表表达式e_i被测试的充分性，即表达式e_i的变异评分.进而可以使用集合S中的所有表达式的变异评分的平均值

$ p = \frac{1}{I}\sum\limits_{i = 1}^I {{p_i}} $

(4)

重新定义被测程序的变异评分.

1) logisitc回归模型  当软件缺陷m_ij被测试用例序列执行时，测试用例序列不能识别出该缺陷的概率可以表示为逐个测试用例不能识别出该缺陷的条件概率q_ijk的乘积.因为条件概率q_ijk位于0与1之间，所以最初想法是采用logistic回归模型^[16]建立条件概率q_ijk与缺陷暴露概率x_ij和缺陷上的测试用例执行序号k之间的回归关系

$ {\rm{logit}}\left( {{q_{ijk}}} \right) = \log \frac{{{q_{ijk}}}}{{1 - {q_{ijk}}}} = {\eta _{rs}}\left( {{x_{ij}},k} \right) $

(5)

即

$ {q_{ijk}} = {\rm{logi}}{{\rm{t}}^{ - 1}}\left[ {{\eta _{rs}}\left( {{x_{ij}},k} \right)} \right] $

(6)

在logisitc回归模型理论中，η_rs被称为线性预测器，是以数字β₀和向量β为系数，以x_ij和k为自变量的多项式

$ \begin{array}{*{20}{c}} {{\eta _{rs}}\left( {{x_{ij}},k} \right) = {\beta _0} + \sum\limits_{u = 1}^r {{\beta _u}x_{ij}^u} + \sum\limits_{v = 1}^s {{\beta _{r + v}}{k^v}} + }\\ {\sum\limits_{v = 1}^s {\sum\limits_{u = 1}^r {{\beta _{s + vr + u}}x_{ij}^u{k^v}} } } \end{array} $

(7)

其中：r与s分别代表了x_ij和k的最高次数，不同的r与s对应了不同的logistic模型c_rs.例如

$ {\eta _{12}}\left( {{x_{ij}},k} \right) = {\beta _0} + {\beta _1}{x_{ij}} + {\beta _2}k + {\beta _3}{k^2} + {\beta _4}{x_{ij}}k + {\beta _5}{x_{ij}}{k^2}. $

1) 预变换  但上述logistic回归模型中存在缺点. η_rs是关于x_ij和k的普通多项式，不能保证x_ij趋近0时q_ijk一定趋近1，也不能保证x_ij趋近1时，q_ijk一定趋近0.于是我们提出如下数据变换方法来解决这个问题：令

$ {z_{ij}} = \log \left[ {\left( {1 - {x_{ij}}} \right)/{x_{ij}}} \right] $

(8)

再以z_ij代替x_ij进入线性预报器η_rs，构造logistic回归

$ {\rm{logit}}\left( {{q_{ijk}}} \right) = {\eta _{rs}}\left( {{z_{ij}},k} \right) $

(9)

其中

$ \begin{array}{*{20}{c}} {{\eta _{rs}}\left( {{z_{ij}},k} \right) = }\\ {{\beta _0} + \sum\limits_{u = 1}^r {{\beta _u}z_{ij}^u} + \sum\limits_{v = 1}^s {{\beta _{r + v}}{k^v}} + }\\ {\sum\limits_{v = 1}^s {\sum\limits_{u = 1}^r {{\beta _{s + vr + u}}z_{ij}^u{k^v}} } } \end{array} $

(10)

并要求r为奇数.这时如果将q_ijk视为以z_ij为自变量的表达式，不论z_ij趋近于正无穷或者负无穷，q_ijk的取值都由z_ij^r的系数决定.当此系数大于零时，

$ \begin{array}{*{20}{c}} {\mathop {\lim }\limits_{{x_{ij}} \to {0^ + }} {q_{ijk}} = \mathop {\lim }\limits_{{z_{ij}} \to + \infty } {q_{ijk}} = 1}\\ {\mathop {\lim }\limits_{{x_{ij}} \to {1^ - }} {q_{ijk}} = \mathop {\lim }\limits_{{z_{ij}} \to - \infty } {q_{ijk}} = 0} \end{array} $

(11)

当此系数小于零时，

$ \begin{array}{*{20}{c}} {\mathop {\lim }\limits_{{x_{ij}} \to {0^ + }} {q_{ijk}} = \mathop {\lim }\limits_{{z_{ij}} \to + } {q_{ijk}} = 0}\\ {\mathop {\lim }\limits_{{x_{ij}} \to {1^ - }} {q_{ijk}} = \mathop {\lim }\limits_{{z_{ij}} \to - \infty } {q_{ijk}} = 1} \end{array} $

(12)

根据物理意义，回归样本的缺陷检测数据能够呈现出以下趋势：缺陷m_ij不能被第k个测试用例识别的条件概率q_ijk随缺陷暴露概率x_ij的增加而减小.这种现象使得z_ij^r的系数必然大于零，以致式(9)满足x_ij趋近0时，q_ijk趋近1，并且有x_ij趋近1时，q_ijk趋近0.

当式(9)中的系数β₀，β的估计值${\hat \beta _0}$，$\mathit{\boldsymbol{\hat \beta }}$确定之后，可以利用式(8)的逆变换，将q_ijk重新表达成x_ij与k的函数.

2) 惩罚极大似然估计

经过数据预处理之后的logistic回归模型以

$ \begin{array}{*{20}{c}} {l\left( {{\beta _0},\mathit{\boldsymbol{\beta }}} \right) = }\\ {\sum\limits_{i = 1}^I {\sum\limits_{j = 1}^{{n_i}} {\sum\limits_{k = 1}^{{h_i}} {\left( {{y_{ijk}}{\eta _{rs}}\left( {{z_{ij}},k} \right) - } \right.} } } }\\ {\left. {\log \left\{ {1 + \exp \left[ {{\eta _{rs}}\left( {{z_{ij}},k} \right)} \right]} \right\}} \right)} \end{array} $

(13)

表达缺陷检测结果出现的联合概率的对数似然.将对数似然极大化可以获得logistic回归模型的参数β₀，β的估计值${\hat \beta _0}$，$\mathit{\boldsymbol{\hat \beta }}$，从而得到logisitc回归模型c_rs(z, k)的经验回归方程

$ {{\hat q}_{rs}}\left( {z,k} \right) = {\rm{logi}}{{\rm{t}}^{ - 1}}\left[ {{{\hat \eta }_{rs}}\left( {z,k} \right)} \right] $

(14)

虽然对基于条件的缺陷检测结果的联合概率的极大化可以实现logistic回归模型的参数估计，但是logistic回归常常使得拟合出的经验回归方程的震荡幅度大、震荡频率高于真实情况，即引发过拟合现象.

为了防止过拟合，希望采用带有惩罚极大似然估计功能的计算软件求解logistic模型的系数参数.使用惩罚极大似然估计方法对联合概率l(β₀，β)极大化等价于极小化问题

$ \mathop {\arg \min }\limits_\mathit{\boldsymbol{\beta }} - l\left( {{\beta _0},\mathit{\boldsymbol{\beta }}} \right) + \frac{1}{2}\lambda {\left\| \mathit{\boldsymbol{\beta }} \right\|_2} $

(15)

其中λ可以使用交叉验证方法加以选择.

3) 交叉验证

交叉验证^[16]是通过测量经验回归方程的预测误差达到评价模型准确性的手段.交叉验证不但有利于确定模型中的未知参数，还可以比较不同的回归模型的相对优劣.

在利用惩罚logistic回归确定未知参数的过程中，通过确定最优化的惩罚参数λ_opt完成交叉验证过程.最常用的交叉验证是Ψ折交叉验证. Ψ折交叉验证首先将基于条件的缺陷检测结果分成Ψ份，然后依次拿出第φ∈(1，2，…，Ψ)份基于条件的检测结果作为测试集，其余φ-1份基于条件的缺陷检测结果作为训练集.在λ给定条件下，为了在每一个测试集上检验回归效果，一共得到Ψ个经验回归方程${{\hat f}_{ - 1}}, {{\hat f}_{ - 2}}, \cdots, {{\hat f}_{ - \psi }}$. Ψ折交叉验证的得分

$ \begin{array}{*{20}{c}} {v\left( \lambda \right) = \frac{1}{\mathit{\Psi }}\sum\limits_{\varphi = 1}^\mathit{\Psi } {{v_\varphi }\left( \lambda \right)} = }\\ {\frac{1}{{\left| S \right|}}\sum\limits_{i = 1}^I {\sum\limits_{j = 1}^{{n_i}} {\sum\limits_{k = 1}^{{h_i}} {l\left[ {{y_{ijk}},{{\hat f}_{ - \varphi \left( {ijk} \right)}}\left( {{x_{ij}},k,\lambda } \right)} \right]} } } } \end{array} $

(16)

其中V_φ(λ)表示在给定λ的条件下回归模型在测试集φ上的预测的平均损失. |S|代表按照式(1)定义的基于条件的缺陷检测结果的数量，${{\hat f}_{ - \varphi \left( {ijk} \right)}}$代表除去y_ijk所在的测试集φ(ijk)后，使用其余Ψ-1个训练集拟合出的经验回归方程.测试集上暴露概率为x_ij的缺陷被第k个测试用例执行时缺陷不能被识别的条件概率的预测值使用${{\hat f}_{ - \varphi \left( {ijk} \right)}}$(x_ij，k，λ)表示.对于logistic回归而言，每一个样本的预测值的损失^[17]为

$ \begin{array}{*{20}{c}} {l\left[ {{y_{ijk}},{{\hat f}_{ - \varphi \left( {ijk} \right)}}\left( {{x_{ijk}},k,\lambda } \right)} \right] = }\\ { - 2\log \hat f_{ - \varphi \left( {ijk} \right)}^{{y_{ijk}}}\left( {{x_{ijk}},k,\lambda } \right)}\\ { - 2\log {{\left[ {1 - {{\hat f}_{ - \varphi \left( {ijk} \right)}}\left( {{x_{ijk}},k,\lambda } \right)} \right]}^{1 - {y_{ijk}}}}} \end{array} $

(17)

当λ的可选范围属于有限集合{λ₁，λ₂，…，λ_F}时，v(λ₁)，v(λ₂)，…，v(λ_F)中最小者对应的λ作为惩罚logistic回归中最优化的惩罚系数λ_opt.

对于多个模型而言，如果每一个模型都采用惩罚性极大似然估计方法确定未知参数，则可以利用交叉验证得分比较不同模型的准确性.因为交叉验证得分代表了模型的预测效果的损失程度，所以在候选模型中以交叉验证得分最小者为佳.

4) 拟合优度检验

可以通过把实际获得的观测数据与利用经验回归方程生成的仿真数据进行对比，完成欠拟合程度的评估^[18].其根本思想如下：依据经验回归方程构建模型因变量(或因变量的某一个函数)出现的主要区间，如果观测样本(或观测样本的上述函数)不出现在这个主要区间内，则认为经验回归方程不能代表真实的潜在规律，从而拒绝经验回归方程，否则接受经验回归方程.

根据上述思想，设计了一个检验经验回归方程的假设检验方案.首先假定候选模型的经验回归方程恰当地反映了潜在的客观规律，以此作为原假设.对于已经观测到的暴露概率为x_ij的缺陷m_ij，基于式(8)和式(14)以及这个被假设成恰当的经验回归方程${{\hat q}_{rs}}\left( {x, k} \right)$计算出缺陷m_ij不能被其上执行的前k-1个测试用例识别的条件下，不能够被第k个测试用例识别的条件概率

$ {{\hat q}_{ijk}}\left( {{x_{ij}},k} \right) = {\rm{logi}}{{\rm{t}}^{ - 1}}\left[ {{{\hat \eta }_{rs}}\left( {{z_{ij}},k} \right)} \right] $

其中z_ij=log[(1-x_ij)/x_ij].

被观测到缺陷m_ij的基于条件的识别结果y_ijk，可以看成是以${{\hat q}_{ijk}}$为事件发生概率的二元随机变量y_ijk^*的一个典型实现，i=1，2，…，I，j=1，2，…，n_i，k=1，2，…，h_i.以致所有被观测到的y_ijk的函数T^*可以看成是相应的以${{\hat q}_{ijk}}$为事件发生概率的取值为0或1的随机变量y_ijk^*的函数T^*的一个实现.当以所有的随机变量y_ijk^*构造拟合优度检验统计量

$ {T^ * } = \sum\limits_{i = 1}^I {\sum\limits_{j = 1}^{{n_i}} {\sum\limits_{k = 1}^{{h_i}} {\frac{{{{\left( {y_{ijk}^ * - {{\hat q}_{ijk}}} \right)}^2}}}{{{{\hat q}_{ijk}}\left( {1 - {{\hat q}_{ijk}}} \right)}}} } } $

(18)

时，所有被观测到的基于条件的缺陷识别结果y₁₁₁，…，y_InIhI的函数

$ {T_{{\rm{obs}}}} = \sum\limits_{i = 1}^I {\sum\limits_{j = 1}^{{n_i}} {\sum\limits_{k = 1}^{{h_i}} {\frac{{{{\left( {{y_{ijk}} - {{\hat q}_{ijk}}} \right)}^2}}}{{{{\hat q}_{ijk}}\left( {1 - {{\hat q}_{ijk}}} \right)}}} } } $

(19)

构成了上述拟合优度检验统计量T^*的一个观测值.在原假设成立的情况下，T_obs会以大概率成为T^*的典型代表.当它不能成为T^*的典型代表时，应拒绝原假设，丢弃对应候选模型.

2 测试用例集合的检错能力的自动化建模工具介绍

以自动化单元测试系统CTS^[19]作为基础，建模工具的工作过程分成6个阶段：第1阶段获得缺陷检测数据；第2阶段对缺陷检测数据进行预变换；第3阶段建立多个logistic候选回归模型并进行参数估计；第4阶段进行后变换得到以缺陷的检测难度为自变量的候选模型的经验回归方程；第5阶段对候选模型的经验回归方程进行拟合优度检验；第6阶段选择最优经验回归方程，计算新型变异评分.

在第1阶段，当被测试的C语言程序源文件和测试用例集合被输入到自动化建模工具之后，自动化建模工具在控制流程图上以不可重复的随机抽样方式选定50个表达式，构成样本集合S.当被测试程序的表达式总数小于50个时，选中全部表达式构成样本集合S.

然后以样本集合S中的每一个表达式e_i为目标，按照随机方式在控制流程图上选定5条完整路径，调用R语言软件hitandrun，在每一条路径的输入域内以均匀随机的方式生成1个测试用例.

接着自动化建模工具调用CTS中的缺陷注入功能，利用12类精简的C语言变异算子^[20]在样本集合S的每一个表达式上实施一阶变异，产生对应的缺陷文件m_ij.

针对每一个软件缺陷m_ij，执行对应的5个均匀随机测试用例，并将缺陷m_ij被测试用例识别的比例x_ij记为缺陷m_ij的暴露概率，以此表征缺陷m_ij的检测难度.然后将接受评价的测试用例按照其生成的先后顺序在被测试程序上执行，记录暴露概率大于零的软件缺陷m_ij不被在其上执行的前k-1个测试用例识别的条件下，被第k个测试用例识别的结果y_ijk，简称基于条件的识别结果.

为了使得在第3阶段得到的回归模型满足如下2个条件：当缺陷的暴露概率为零时，缺陷不可被任意测试用例检测到；当暴露概率为1时，缺陷必定可以被任意测试用例检测到，在第2阶段，使用式(8)对缺陷的暴露概率x_ij进行预变换，形成z_ij.进而以变换后的缺陷检测数据z_ij，y_ijk，k作为第3阶段回归中的数据样本.

在第3阶段，利用自动化建模工具建立logistic候选回归模型并进行参数估计.缺陷不能被第k个测试用例识别的条件概率q_ijk往往随着在其上执行的测试用例的执行序号k的逐渐增大呈现出以下4种主要趋势：逐渐增大，逐渐减小，先减小再增大，先增大再减小.当logistic模型的线性预报器被表示为缺陷m_ij上的测试用例执行序号k的二次函数(v=2)时，logistic模型可表达上述这4种趋势.于是线性预报器η_rs关于z_ij和k的基本形式为η₁₂(z_ij，k)，即

$ {\beta _0} + {\beta _1}{z_{ij}} + {\beta _2}k + {\beta _3}{k^2} + {\beta _4}{z_{ij}}k + {\beta _5}{z_{ij}}{k^2}. $

事实上，过于复杂的模型很难从物理意义上进行解释，并且对于现实世界中已知的多数规律，都可以通过建立与之对应的简单模型进行近似^[21].为了能够在相对简单的模型中，让拟合出的经验回归方程以更大程度接近真实规律，自动化建模工具设置了与基本形式η₁₂相对接近的6种类型：η₁₁(z_ij，k)，η₁₂(z_ij，k)，η₁₃(z_ij，k)，η₃₁(z_ij，k)，η₃₂(z_ij，k)，η₃₃(z_ij，k).对应形成6个以z_ij和k为自变量的候选logistic模型，模型分别记为c_rs(z, k)，r=1，3，s=1，2，3.

为了计算每一个候选logistic模型c_rs中的待定系数，自动化建模工具将会调用实现了惩罚极大似然估计方法的R语言开源软件包glmnet中的cv. glmnet函数^[22].此函数不仅可以对参数系数β₀，β进行估计，还可获得模型c_rs(z，k)的经验回归方程的交叉验证得分v^rs. cv.glmnet在执行过程中，首先会由大到小产生100个惩罚参数λ₁，λ₂…，λ₁₀₀，其中λ₁趋近于正无穷大量，λ₁₀₀趋近于零，以便在拟合的过程中产生尽可能不同的100个经验回归方程，然后cv. glmnet从中挑选具有最小交叉验证得分的经验回归方程作为模型c_rs(z，k)的经验回归方程.

第4阶段利用式(8)的反变换对第3阶段拟合出的每一个候选logistic模型c_rs(z，k)的经验回归方程${{\hat q}_{rs}}\left( {z, k} \right)$进行后变换，得到以缺陷暴露概率x为自变量的模型c_rs(x，k)的经验回归方程${{\hat q}_{rs}}\left( {x, k} \right)$.

第5阶段对第4阶段得到的每一个候选模型的经验回归方程${{\hat q}_{rs}}\left( {x, k} \right)$进行拟合优度检验.对于每一个经验回归方程${{\hat q}_{rs}}\left( {x, k} \right)$，自动化建模工具首先建立原假设H₀：候选模型的经验回归方程${{\hat q}_{rs}}\left( {x, k} \right)$能够恰当表达测试用例集合的检错能力.以经验回归方程${{\hat q}_{rs}}\left( {x, k} \right)$为依据，自动化建模工具利用式(18)产生检验统计量T^*的B=1 000个随机实现T_b，b=1，2，…，B.以由小到大排序这B个实现.如果T_b位于排序中的第r个位置，则将T_b记为T_(r).将0.025×B向上取整记为l_b，0.755×B向下取整记为u_b.如果T_obs≤T_(lb)或者T_obs≥T_(ub)，说明构成T_obs的|S|个基于条件的缺陷检测结果的发生是小概率发生事件，从而拒绝原假设，丢弃经验回归方程${{\hat q}_{rs}}\left( {x, k} \right)$，否则保留经验回归方程${{\hat q}_{rs}}\left( {x, k} \right)$.

第6阶段进行经验回归方程的选择.交叉验证得分可以表达经验回归方程的预测误差，从而可以评价模型的相对准确性.自动化建模工具利用式(16)，从第5阶段保留的所有候选经验回归方程${{\hat q}_{rs}}\left( {x, k} \right)$中挑选出具有最小交叉验证得分者作为最佳的经验回归方程来表达缺陷被识别的条件概率与缺陷的检测难度以及被测试用例执行的序号之间的联系.

自动化建模工具可以使用式(2)进一步产生缺陷被识别的概率与缺陷的检测难度以及被测试用例执行次数之间的函数关系p(x，k).接着，自动化建模工具利用式(3)和式(4)分别计算出被测试程序的每一个表达式的变异评分以及被测试程序的变异评分.

3 自动化建模工具的使用及其实验

使用的被测试程序是一个真实的三角形类型判定程序tri.c.测试用例集合包含了由自动化单元测试系统CTS针对tri.c按照语句覆盖准则产生的6个测试用例.测试用例按照产生的时间排序为tc₁、tc₂、tc₃、tc₄、tc₅、tc₆.自动化建模工具对这个达到语句覆盖标准的测试用例集合的检错能力进行了建模.

在第1阶段，自动化建模工具调用CTS系统中的缺陷注入功能，对表达式样本集S使用了算数运算符替代、常量替代、关系运算符替代等12类精简的变异算子^[20]，一共播种了181个变异缺陷，构造了399个基于条件的缺陷检测结果.每一个基于条件的缺陷检测结果都记录了之前若干个测试用例不能识别该缺陷的条件下缺陷被下一个测试用例识别的结果.然后自动化建模工具会在缺陷文件上执行测试用例，计算缺陷样本的检测难度.

在第2阶段，自动化建模工具按照式(8)对缺陷样本的暴露概率x_ij进行预变换，将其转化为z_ij.在第3节阶段，自动化建模工具调用开源软件包glmnet中的cv.glmnet函数分别对第2节中描述的6个logistic候选模型c_rs(z, k)的系数β₀，β进行了估计.在cv.glmnet利用惩罚性极大似然估计方法确定模型中的未知系数的过程中采用了10折交叉验证方案，从而得到了每一个logistic模型的经验回归方程${{\hat q}_{rs}}\left( {z, k} \right)$.

在cv.glmnet利用惩罚性极大似然估计方法确定模型中的未知系数的过程中，cv.glmnet还提供了每一个经验回归方程${{\hat q}_{rs}}\left( {z, k} \right)$的交叉验证得分，用以表达经验回归方程相对准确性.

在第4阶段利用式(8)的反变换对第3阶段拟合出的6个候选logistic模型c_rs(z, k)的经验回归方程${{\hat q}_{rs}}\left( {z, k} \right)$进行后变换，得到以缺陷的检测难度x和在缺陷上执行测试用例的序号k为自变量经验回归方程

$ {{\hat q}_{rs}}\left( {x,k} \right) = {{\hat q}_{rs}}\left[ {z\left( x \right),k} \right] $

其中z(x)=log[(1-x)/x]，r=1，3，s=1，2，3.

在第5阶段，自动化建模工具对第4阶段得到的每一个经验回归方程${{\hat q}_{rs}}\left( {x, k} \right)$进行拟合优度检验.构造拟合优度检验统计量T^*的1 000个实现T₁，T₂，…，T_{1 000}，从而仿真出拟合优度检验统计量T^*的概率分布.最后自动化建模工具以递增的顺序排列此1 000个实现，从而获得拟合优度检验统计量T^*的95%置信区间的上界T_(ub)和下界T_(lb).

接着自动化建模工具判断每一个经验回归方程${{\hat q}_{rs}}\left( {x, k} \right)$的拟合优度统计量的观测值T_obs与95%置信区间的上界T_(ub)和下界T_(lb)之间的关系.实验数据表明，每一个候选的经验回归方程的拟合优度检验统计量的观测值都处于拟合优度检验统计量的置信区间的上界和下界之间.因此，自动化建模工具没有淘汰任何一个候选模型的经验回归方程.自动化建模工具在第6阶段对第5阶段保留的6个候选经验回归方程进行交叉验证得分的比较.交叉验证得分可以表达经验回归方程的预测误差，从而可以评价模型的相对准确性.经验回归方程${{\hat q}_{31}}\left( {x, k} \right)$的交叉验证的得分在6个经验回归方程中最小，成为最佳的经验回归方程，最终得到的经验回归方程为

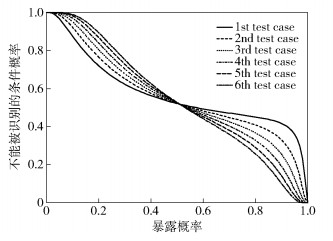
$ \begin{array}{*{20}{c}} {\hat q\left( {x,k} \right) = {\rm{logi}}{{\rm{t}}^{ - 1}}\left[ {0.081 + 0.225z + 0.134{z^2} + } \right.}\\ {\left. {0.019{z^3} + 0.003k + 0.112zk + 0.014{z^2}k + 0.018{z^3}k} \right)} \end{array} $

其中z=log[(1-x)/x].如图 1所示，$\hat q\left( {x, k} \right)$)表达了暴露概率为x的缺陷不被在其上执行的k-1测试用例识别的条件下，依然不被第k个测试用例识别的概率.

自动化建模工具可以进一步产生缺陷被识别的概率与缺陷的检测难度之间的函数关系:

$ p\left( {x,k} \right) = 1 - q\left( {x,1} \right) \cdots q\left( {x,k} \right) $

这时，表达式被测试用例执行的次数k被视为已知量.最后自动化建模工具将所有表达式样本的变异评分的平均值0.68作为被测试程序的变异评分.

4 结束语

给出了一种基于缺陷检测难度建模测试用例集合的检错能力的方法.这种方法不但能够表达缺陷被检测到的概率与缺陷检测难度之间的数量关系，还能够表达测试用例按照其产生时间的先后顺序呈现出的检错能力的变化趋势.重新定义的被测试程序的变异评分规避了经典变异评分的计算过程中因被播种的缺陷集的检测难度的变化而使得变异评分的计算不稳定的缺点.目前的自动化建模工具的建模对象只能是由数值运算构成的单个被测试函数.下一步的工作重点是扩大自动化建模工具的适用范围，使得自动化建模工具可以适用于包含有函数调用以及字符串、结构体等复杂数据结构的C语言被测试程序.