2. 上海海事大学 信息工程学院, 上海 201306
基于记忆的人工蜂群算法(ABCM)通过记住成功使用的邻居和系数指导人工蜂群下一步的搜索,需消耗多次函数评价收敛到吸引子,且始终使用与上次相同的排斥系数,造成收敛速度不快、多样性不足,易陷入局部最优解.提出一种改进ABCM(IABCM),当使用吸引系数时,候选解只消耗一次函数评价收敛到吸引子,如果候选解好于当前解,则替换当前解,否则直接删除该记忆,这样可以利用尽量小的代价得到尽量大的收益.当使用排斥系数时,该系数的数值部分重新随机生成,以增加多样性和随机性,有利于算法跳出局部最优解.在22个不同类型函数上的实验表明,IABCM在收敛速度和精度方面明显优于ABCM.
2. College of Information Engineering, Shanghai Maritime University, Shanghai 201306, China
Artificial bee colony algorithm with memory (ABCM) memorizes successful coefficients and neighbors to guide the further foraging of the artiflcial bees. ABCM consumes many function evaluations to converge to the attractors and use the same rejection coefficients as last time, which easily results in slow convergence, low population diversity and falling into the local minima. In the improved ABCM (IABCM), the candidates converge to the attractors consuming only one function evaluation, and the candidate will replace the current solution if the former is better than the latter. Otherwise, the memory will be deleted directly. By doing so, IABCM can get the most profit at a minimum cost. When the rejection coefficients are used, the numeric parts will be regenerated randomly to enhance the diversity and randomness, which is beneficial to help the algorithm to escape the local minima. Experiments on 22 functions with different characteristics demonstrate that the IABCM is significantly better than ABC and ABCM in terms of solution quality and convergence speed.
进化算法在解决图像处理、数据挖掘、特征选择等领域的复杂优化问题方面取得了显著的成绩, 受到越来越多的关注.主要的进化算法包括遗传算法[1]、粒子群算法[2]、蚁群算法[3]、差分进化算法[4]、人工蜂群算法[5](ABC, artificial bee colony)等. Karaboga等[6-8]的实验结果表明ABC的性能好于、至少相当于其他群体智能优化算法, 加上ABC比较容易实施, 因此得到了广泛的研究和应用[9-10].在ABC中, 可以用先前的成功经验指导蜂群下一步的搜索. Kiran等[11]通过增加记忆库记住精英解, 使用精英解作为搜索公式中的邻居来增加ABC的开采性能. Gao等[12]也提出了一种类似于记忆的机制来决定每个个体每次搜索使用的参数, 统计上一代的所有个体搜索成功时使用的参数的均值决定下一次某个个体使用的参数.以上几种改进都只是在解的水平, 属于粗粒度记忆, 没有针对某一个具体的个体. Li等[13]提出了一种带记忆的ABC(ABCM, artificial bee colony with memory), 采用不同于上述文献的记忆机制, 进一步细化了记忆机制, 同时记住每个个体每一次成功搜索时使用的邻居和参数, 取得了一定的优势.但是, ABCM仍然存在收敛速度不够快、精度不够高的缺点.笔者在ABCM的基础上, 进一步细化了记忆机制, 在保持复杂度不变的情况下, 改变ABCM中记忆的使用方式, 在22个不同类型函数上的测试结果表明, 改进算法明显提高了ABCM的性能.
1 ABC在ABC[5]中, 雇佣蜂负责勘探食物源, 并将食物源的信息通过舞蹈的形式通知观察蜂;观察蜂根据雇佣蜂带来的信息, 按照一定的概率选择某个食物源继续进行开采.食物源被选中的概率与食物源的质量成正比.如果一个食物源的适应度连续l次未能成功更新, 则需要放弃该位置.这时, 该食物源对应的雇佣蜂转变为侦察蜂, 随机侦察(初始化)一个新的食物源代替该食物源.在ABC中, 雇佣蜂和观察蜂的数量都等于N.设待优化问题是求最小值, 首先按照式(1) 随机生成N个初始解.
| $ x_i^j = x_{\min }^j + {\rm{rand}}\left( {0,1} \right)\left( {x_{\max }^j - x_{\min }^j} \right) $ | (1) |
其中:rand(0, 1) 是[0, 1]之间的随机数; i=1, 2, …, N; j=1, 2, …, D, D是决策变量的数量, 也就是待优化问题的维数; xmaxj和xminj分别是第j维的上界和下界.初始化之后, ABC按以下3个阶段搜索问题的最优解.
1) 雇佣蜂阶段:每只雇佣蜂在相应的食物源xi处, 利用式(2) 随机选择第j维更新, 生成新的食物源vi.
| $ v_i^j = x_i^j + \delta _i^j\left( {x_k^j - x_i^j} \right) $ | (2) |
其中:φij是[-1, 1]之间的随机数, j∈{1, 2, …, D}是随机选择的一个维, k是{1, 2, …, N}中随机选择的一个不同于i的食物源.发现新的食物源vi之后, 如果vi的函数值f(vi)小于xi的函数值f(xi), 就称搜索xij成功, 用vi替换xi, 否则xi保持不变.
2) 观察蜂阶段:在所有雇佣蜂完成了勘探之后, 观察蜂根据接收到的信息随机选择一个食物源继续开采.观察蜂按照式(3) 选择食物源.
| $ {p_i} = {a_i}/\sum\limits_{i = 1}^N {{a_i}} $ | (3) |
其中ai是食物源i的适应度值.选择食物源之后, 观察蜂用式(2) 搜索新的候选解, 如果搜索的新解的适应度更好, 则替换掉原食物源, 否则原食物源保持不变.对于最小值优化问题, ai由式(4) 给出.
| $ {a_i} = \left\{ \begin{array}{l} 1/\left( {1 + {o_i}} \right),\;\;\;\;若\;{o_i} \ge 0\\ 1 + \left| {{o_i}} \right|,\;\;\;\;其他 \end{array} \right. $ | (4) |
其中oi是食物源i的目标函数值.
3) 侦察蜂阶段:若每个食物源i使用式(2) 搜索失败, 则失败次数Ti=Ti+1.在每一轮迭代中, 只选择T值最大且超过l的食物源初始化.即如果max(Ti)>l, 则食物源i被抛弃, 该食物源对应的雇佣蜂成为侦察蜂, 该侦察蜂按照式(1) 通过初始化被抛弃的食物源代替被抛弃的食物源i.
2 ABCMGiurfa[14]对蜜蜂等昆虫的记忆行为从神经科学的角度进行了深入的研究, 结论表明真实的蜜蜂具有非凡的联想记忆能力, 从而可以利用先前成功的经验指导后续搜索行为.但是, 这种记忆能力在基本ABC算法及其改进版本中没有得到体现, 如式(2) 所示, 每一个雇佣蜂或者观察蜂都随机地选择一个邻居k开采. Li等[13]通过引入记忆结构, 模仿了蜜蜂的记忆能力, 允许蜜蜂记住先前的成功搜索经验.记忆结构随时更新, 可以用来指导蜜蜂的后续搜索行为, 使得搜索比ABC更加有效.
2.1 记忆结构Li等[13]提出的ABCM中, xij的记忆用Mij表示, 其中i=1, 2, …, N表示食物源序号, j=1, 2, …, D表示变量的维数, 整个记忆库表示为式(5).开始
| $ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {M_1^1}&{M_1^2}& \cdots &{M_1^D}\\ {M_2^1}&{M_2^2}& \cdots &{M_2^D}\\ \vdots&\vdots&\ddots&\vdots \\ {M_N^1}&{M_N^2}& \cdots &{M_N^D} \end{array}} \right] $ | (5) |
时, 每个记忆Mij为空, 随着ABC算法的不断迭代, Mij不断地根据雇佣蜂和观察蜂的成功搜索经验更新.具体地, 如果一个雇佣蜂或者观察蜂利用式(2) 搜索xij成功(o(vi) < o(xi)), 相应的更新信息被视为成功的搜索经验并且保存在记忆Mij中. Mij将记住式(2) 的2个成分:所使用的邻居k;所使用的系数φij.
换句话说, 如果式(2) 用过的值k和φij能够成功地更新xij, 则k和φij将被作为成功经验保存到记忆Mij中, 以供下次再次使用. 表 1给出了xij的记忆结构Mij.其中, M表示记忆容量, 对于xij, 其对应的记忆结构Mij包含成功搜索时的邻居kij(m)和成功搜索时的系数φij(m), m=1, 2, …, M, i=1, 2, …, N, j=1, 2, …, D.
|
|
表 1 记忆的结构 |
在基本ABC中, 当完成式(2) 的时候, 随机选择邻居k和系数φij.在ABCM中, 当记忆未满的时候, 与ABC一样随机选择邻居k和系数φij;当记忆已满的时候, 改用记忆中对应的邻居k和系数φij完成式(2), 也即此时蜜蜂继续使用以前成功的经验.
2.3 记忆的更新开始的时候, 每个食物源的每一维的记忆Mij为空.在进化过程中, 如果xij使用式(2) 搜索成功, 则使用过的邻居k和系数φij被保存到xij对应的记忆Mij中.当记忆未满的时候, ABCM与ABC一样随机选择式(2) 的邻居k和系数φij.当记忆已满的时候, 邻居k和系数φij从Mij的M条记忆中随机选择一条(表 1中的任意一行)记忆.如果使用该记忆搜索成功, 则该条记忆继续保持, 否则该条记忆删除.
3 改进算法在ABCM中, 当xij的记忆Mij中的系数φij大于0时, 笔者借用物理学中的概念, 称为吸引系数, 对应的邻居xk称为吸引子; 当φij小于0时称为排斥系数, 对应的邻居xk称为排斥子. ABCM第1次使用吸引系数与吸引子的方式为
| $ v_i^j = x_i^j\left( 1 \right) + \phi _i^j\left( {x_k^j - x_i^j\left( 1 \right)} \right) $ | (6) |
其中:第1次使用该记忆时的xij称为xij(1).假设第1次记忆使用成功, 根据式(2), 应该用vij代替xij, 此时xij=vij=xij(1) +φij(xkj-xij(1)), xij得到成功更新.同时, 根据ABCM的原理, 该记忆被保持在Mij中, 邻居k和系数φij保持不变, 供下次继续使用.第2次使用该记忆时:
| $ \begin{array}{*{20}{c}} {v_i^j = x_i^j\left( 2 \right) + \phi _i^j\left( {x_k^j - x_i^j\left( 2 \right)} \right) = }\\ {\underbrace {x_i^j\left( 1 \right) + \phi _i^j\left( {x_k^j - x_i^j\left( 1 \right)} \right)}_{x_i^j\left( 2 \right)} + }\\ {\phi _i^j\left[ {x_k^j - \underbrace {\left( {x_i^j\left( 1 \right) + \phi _i^j\left( {x_k^j - x_i^j\left( 1 \right)} \right)} \right)}_{x_i^j\left( 2 \right)}} \right] = }\\ {\underbrace {x_i^j\left( 1 \right) + 2\phi _i^j\left( {x_k^j - x_i^j\left( 1 \right)} \right) - {{\left( {\phi _i^j} \right)}^2}\left[ {x_k^j - x_i^j\left( 1 \right)} \right]}_{x_i^j\left( 3 \right)}} \end{array} $ | (7) |
由于φij < 1, 所以第3项的系数(φij)2相对于第2项的系数2φij是一个很小的数值, 第3项可以忽略不计, 式(7) 可以简化为
| $ v_i^j = x_i^j\left( 1 \right) + 2\phi _i^j\left( {x_k^j - x_i^j\left( 1 \right)} \right) $ | (8) |
同理, 可以推得第3次使用该记忆的递推公式:
| $ v_i^j = x_i^j\left( 1 \right) + 3\phi _i^j\left( {x_k^j - x_i^j\left( 1 \right)} \right) $ | (9) |
类似地, 可得出第n次使用记忆的近似递推公式为
| $ v_i^j = x_i^j\left( 1 \right) + n\phi _i^j\left( {x_k^j - x_i^j\left( 1 \right)} \right) $ | (10) |
其中:nφij是吸引系数, xkj是xij的吸引子.当吸引系数nφij>1时无意义, 因此nφij最多取1.也就是说, 若xij的记忆可以使用n次, 将消耗n次函数评价, 而其最终结果与只使用式(11) 一次近似等价.
| $ v_i^j = x_i^j\left( 1 \right) + 1 \times \left( {x_k^j - x_i^j\left( 1 \right)} \right) $ | (11) |
式(11) 相当于式(2) 中φij=1的情况.这意味着, 如果在使用记忆的时候, 令φij=1, 直接使用式(11), 将会节省中间n-1次函数评价, 而最终的结果近似相同.
根据基本ABC的搜索式(2), 当系数φij < 0时, 式(2) 右边的第2项φij(xkj-xij)代表排斥项, 此时的xk与φij>0时的意义不同, 不代表好于xi的吸引子, 相反, 代表差于xi的排斥子.与吸引系数不同, 排斥系数φij的数值部分|φij|没有具体的意义.因此在改进ABCM(IABCM, improved ABCM)中, 当φij < 0时, 采用式(12) 重新生成新的排斥系数φij.
| $ \phi _i^j = {\rm{rand}}\left( { - 1,0} \right) $ | (12) |
其中rand(-1, 0) 代表[-1, 0]之间的随机数.与ABCM相比, IABCM采用式(12), 每次使用排斥系数φij的时候, 只使用了φij的符号, 而其数值部分|φij|重新随机生成, 增加了多样性和随机性.
IABCM算法的流程如下:
步骤1 初始化种群, 设置记忆库B为空, g=1.
//雇佣蜂阶段
步骤2 当迭代代数g小于最大允许迭代次数时, 执行以下步骤.
步骤2.1 每个食物源i(1≤i≤N)执行以下步骤:
1) 如果Mij未满, 则执行搜索式(2), 若搜索到更好的解, 则将使用过的k与φij保存到Mij.
2) 如果Mij已满, 随机从记忆Mij中取出一条记忆, 包含成功使用过的邻居k与对应的系数φij.对取出的系数φij做如下修正:若φij>0, 则令φij=1;否则, 令φij为[-1, 0]之间的随机数.利用取出的邻居k与修正的系数φij完成式(2).如果未搜到更好的解或者系数φij>0, 从记忆Mij中删除该次使用的邻居k及相应的系数φij.
步骤2.2 计算每个食物源i对应的选择概率pi.
//观察蜂阶段
步骤2.3 对每只观察蜂t(1≤t≤N)执行以下操作:
根据概率pi轮盘赌选择一个食物源i, 执行步骤2.1.
//侦察蜂阶段
步骤2.4 每一轮迭代选择一个T值最大的食物源i, 若Ti>l, 利用式(1) 初始化食物源i, 其相应的记忆置空.
步骤2.5 g=g+1, 若满足终止条件, 转到步骤3, 否则返回步骤2.
步骤3 输出全局最优解, 算法结束.
IABCM与ABCM的区别仅在于使用记忆的方式不同. IABCM使用记忆的过程如下:
1) 当xij的记忆Mij未满的时候, 每当使用式(2) 搜索到一个更好的解vi, 则将使用的邻居k和系数φij保存到记忆Mij中. (见步骤2.1的1))
2) 当xij的记忆Mij已满的时候, 随机从Mij中取出一条记忆, 该条记忆包含对应的邻居k和系数φij.如果φij大于0(吸引系数), 则φij赋值为1再使用.如果φij小于0(排斥系数), 则φij仍然保持符号为负号, 而其数值部分在[-1, 0]之间随机生成.根据邻居k和修改的系数φij完成式(2).之后, 如果φij是吸引系数, 则不管搜索是否成功, 都会删除该系数对应的整条记忆;如果φij是排斥系数, 仅在搜索失败的时候删除整条记忆.
4 实验与分析 4.1 测试函数与参数设置实验采用Gao等[12, 15-16]等广泛使用的22个测试函数, 这些函数的定义见文献[16], 包含22个不同类型的函数, 其中f1~f6与f8是连续的单峰函数, f7是不连续的函数, f9是含有噪声的函数, f10当D>3时是多峰函数, f11~f22是多峰函数, 测试结果如表 2所示. 表 2最后一行给出了Wilcoxon[17]非参数统计结果(显著性水平为0.05), “+”、“=”、“-”的含义分别表示IABCM好于、等于、差于被比较的算法.设置参数N=50, D=30, M=2, l=D×N. maxFES表示最大函数评价次数, 作为算法的结束条件, 设置maxFES=50 000.实验在相同条件下重复30次.
|
|
表 2 ABC、ABCM与IABCM在22个测试函数上的实验结果(D=30) |
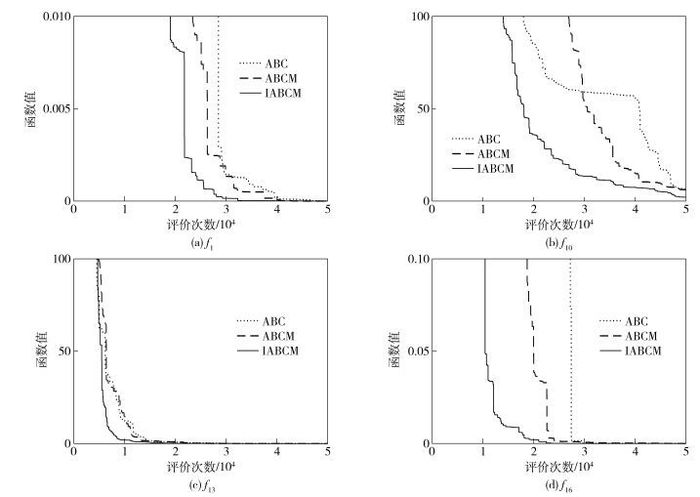
根据表 2, IABCM在22个函数上, 有17个函数的求解精度明显好于ABC和ABCM, 1个函数(f7)上3种算法求解精度相同, 显示IABCM具有较大的优势.在单峰函数f1~f9上, IABCM的求解精度只在f9上不如ABCM, 在其余8个函数上都取得了最好的结果.这主要是因为当φij大于0时, 直接取φij=1, 节省了函数评价次数.所有算法在f7函数上都求得了理论最优解0, 这主要是因为f7的理论最优解是一个区域, 而不是一个点, 因此非常容易求解[16].在多峰函数f11~f22上, 只有在f11、f12、f14上稍差于其他算法, 在其余9个函数上都取得了最好的结果.这主要是因为IABCM在使用记忆的时候, 当系数φij小于0时, 只使用系数φij的符号(负号), 而其数值部分在每次使用的时候都随机生成, 增加了多样性和随机性, 有利于算法在多峰函数中跳出局部最优解.根据无免费午餐定理, 一种策略带来优点的同时, 总会带来一定的缺点, IABCM由于直接取吸引系数φij=1, 有利于算法快速向吸引子收敛, 减小了算法的盲目搜索, 但也会导致算法比较贪婪, 从而在少数多峰函数f11、f12、f14上稍差于ABCM, 但是从总体上看, IABCM在多数函数上仍然明显好于ABCM. 图 1给出了ABC、ABCM与IABCM的收敛曲线, 从图中可以看出, IABCM比ABC、ABCM有更快的收敛速度, 且IABCM对比ABCM的优势明显大于ABCM对于ABC的优势.
|
图 1 3种算法在4个函数上的收敛曲线 |
ABC算法因为简单高效、容易实施, 从而获得了广泛应用.如何在保持算法简单性的同时提高算法的性能, 是改进算法的挑战.笔者在ABCM的基础上, 没有引入新的结构, 也没有增加算法复杂度, 仅仅改变了ABCM中记忆的使用方式, 明显提高了ABCM的性能, 改进算法依然保持了ABCM的简单、易实施的特点, 容易作为通用框架推广到其他改进ABC算法.
| [1] | Tang K S, Man K F, Kwong S, et al. Genetic algorithms and their applications[J]. IEEE Signal Processing Magazine, 1996, 13(6): 22–37. doi: 10.1109/79.543973 |
| [2] | Kennedy J, Eberhart R. Particle swarm optimization[C]//Proc of IEEE Int Conf on Neural Networks. Piscataway:IEEE, 1995:1942-1948. |
| [3] | Dorigo M, Maniezzo V, Colorni A. Ant system:optimization by a colony of cooperating agents[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 1996, 26(1): 29–41. doi: 10.1109/3477.484436 |
| [4] | Storn R, Price K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4): 341–359. doi: 10.1023/A:1008202821328 |
| [5] | Karaboga D. An idea based on honey bee swarm for numerical optimization[R]. Kayseri:Engineering Faculty Computer Engineering Department, Ereiyes University, 2005. |
| [6] | Karaboga D, Basturk B. On the performance of artificial bee colony (ABC) algorithm[J]. Applied Soft Computing, 2008, 8(1): 687–697. doi: 10.1016/j.asoc.2007.05.007 |
| [7] | Karaboga D, Akay B. A comparative study of artificial bee colony algorithm[J]. Applied Mathematics and Computation, 2009, 214(1): 108–132. doi: 10.1016/j.amc.2009.03.090 |
| [8] | Pholdee N, Bureerat S. Comparative performance of metaheuristic algorithm for mass minimission of trusses with dynamic constraints[J]. Advances in Engineering Software, 2014, 75(9): 1–13. |
| [9] | Tasgetiren M F, Pan Q K, Suganthan P N, et al. A discrete artificial bee colony algorithm for the total flowtime minimization in permutation flow shops[J]. Information Sciences, 2011, 181(16): 3459–3475. doi: 10.1016/j.ins.2011.04.018 |
| [10] | Lozano M, García-Martínez C, Rodríguez F J, et al. Optimizing network attacks by artificial bee colony[J]. Information Sciences, 2017, 377(1): 30–50. |
| [11] | Kiran M S, Babalik A. Improved artificial bee colony algorithm for continuous optimization problems[J]. Journal of Computer and Communications, 2014, 2(04): 108–116. doi: 10.4236/jcc.2014.24015 |
| [12] | Gao Weifeng, Chan F T S, Huang Lingling, et al. Bare bones artificial bee colony algorithm with parameter adaptation and fitness-based neighborhood[J]. Information Sciences, 2015, 316(18): 180–200. |
| [13] | Li Xianneng, Yang Guangfei. Artificial bee colony algorithm with memory[J]. Applied Soft Computing, 2016, 41(4): 362–372. |
| [14] | Giurfa M, Zhang Shaowu, Jenett A, et al. The concepts of 'sameness' and 'difference' in an insect[J]. Nature, 2001, 410(6831): 930–933. doi: 10.1038/35073582 |
| [15] | Gao Weifeng, Liu Sanyang, Huang Lingling. A novel artificial bee colony algorithm based on modified search equation and orthogonal learning[J]. IEEE Transactions on Cybernetics, 2013, 43(3): 1011–1024. doi: 10.1109/TSMCB.2012.2222373 |
| [16] | Cui Laizhong, Li Genghui, Lin Qiuzhen, et al. A novel artificial bee colony algorithm with depth-first search framework and elite-guided search equation[J]. Information Sciences, 2016, 367(18): 1012–1044. |
| [17] | Derrac J, García S, Molina D, et al. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms[J]. Swarm and Evolutionary Computation, 2011, 1(1): 3–18. doi: 10.1016/j.swevo.2011.02.002 |


