2. 中国民用航空飞行学院, 四川 德阳 618300
基于Jacobi迭代提出一种低复杂度信号检测算法,在算法实现中避免了矩阵求逆运算.数学推导证明,该算法应用于MMSE检测时是收敛的,与传统的Neumann级数展开方法对比,能达到与其完全相同的检测性能,并且在任意迭代次数下能将复杂度保持在O(K2),而后者当级数展开项数大于等于3时复杂度上升为O(K3).为了进一步将Jacobi迭代应用到软判决中,提出了一种用于信道译码的LLR的近似计算方法.仿真结果表明,经过几次迭代,Jacobi迭代算法收敛较快,并接近MMSE检测性能.
2. Civil Aviation Flight University of China, Sichuan Deyang 618300, China
Based on Jacobi iterative method, a low-complexity detection algorithm which can circumvent the matrix inverse operation was proposed. The proposed algorithm was proved to be convergent when it is applied in the MMSE detection scheme, and it can achieve the same performance of the classical Neumann series expansion. Unlike conventional Neumann method with the number of iterations exceeding three (i ≥ 3), whose computational complexity is increasing to O(K3), the proposed algorithm can keep it consistently at O(K2) with arbitrary number of iterations. In order to employ that in soft decision, an approximated method was adopted to compute log-likelihood ratios for soft channel decoding. Simulations verify that the proposed algorithm can converge rapidly and achieve its performance quite close to that of the MMSE algorithm with only a small number of iterations.
大规模多输入多输出(MIMO, multiple-input multiple-output)系统能够以2~3个数量级的程度提升无线通信系统的频谱利用率和功率利用率[1-3], 已成为5G最具潜力的使能技术和热点研究方向之一.最小均方误差(MMSE, minimum mean square error)检测算法已广泛应用于大规模MIMO系统中, 可以实现接近最优的检测性能, 但这类检测算法引入了复杂度较高(O(K3))的高维矩阵求逆运算. Wu等[4]、Kang等[5]以及Tang等[6]基于Neumann级数展开提出了一系列低复杂度解决方案, 仅仅将3级展开复杂度降低到O(K2).
笔者利用Jacobi迭代[7]与Neumann级数展开之间的关系, 提出一种基于Jacobi迭代的低复杂度检测算法, 理论和仿真结果均证明该算法可以在迭代次数比Neumann级数展开项数少1的情况下实现与其完全相同的检测性能, 从而等效地实现将任意项数展开的Neumann级数计算复杂度保持在O(K2).此外, 为了充分利用软信息并将其应用到软判决中, 给出了一种对数似然比(LLR, log-likelihood ratio)的近似计算方法, 并通过仿真验证了检测性能.
1 系统模型考虑大规模MIMO系统上行链路, 该系统由一个配备N根天线的基站和K个单天线用户组成且满足N≫K.令sc=[s1, s2, …, sK]T表示所有用户同时发送的K×1维符号向量, 其中sk∈
| $ {\mathit{\boldsymbol{y}}_c} = {\mathit{\boldsymbol{H}}_c}{\mathit{\boldsymbol{s}}_c} + {\mathit{\boldsymbol{n}}_c} $ | (1) |
其中nc是N×1维均值为0、协方差矩阵为σ2IN的加性高斯白噪声向量.式(1) 转化为等价实数模型为
| $ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{Hs}} + \mathit{\boldsymbol{n}} $ | (2) |
其中:s∈ℝ2K, H∈ℝ2N×2K, y∈ℝ2N, n∈ℝ2N, 即有
| $ \mathit{\boldsymbol{H}} = \left[ {\begin{array}{*{20}{c}} {\Re \left( {{\mathit{\boldsymbol{H}}_c}} \right)}&{ - \Im \left( {{\mathit{\boldsymbol{H}}_c}} \right)}\\ {\Im \left( {{\mathit{\boldsymbol{H}}_c}} \right)}&{\Re \left( {{\mathit{\boldsymbol{H}}_c}} \right)} \end{array}} \right],\mathit{\boldsymbol{y}} = \left[ {\begin{array}{*{20}{c}} {\Re \left( {{\mathit{\boldsymbol{y}}_c}} \right)}\\ {\Im \left( {{\mathit{\boldsymbol{y}}_c}} \right)} \end{array}} \right], $ |
| $ \mathit{\boldsymbol{s}} = \left[ {\begin{array}{*{20}{c}} {\Re \left( {{\mathit{\boldsymbol{s}}_c}} \right)}\\ {\Im \left( {{\mathit{\boldsymbol{s}}_c}} \right)} \end{array}} \right],\mathit{\boldsymbol{n}} = \left[ {\begin{array}{*{20}{c}} {\Re \left( {{\mathit{\boldsymbol{n}}_c}} \right)}\\ {\Im \left( {{\mathit{\boldsymbol{n}}_c}} \right)} \end{array}} \right] $ |
其中
通过MMSE滤波, 基站接收端对发送信号矢量s的估计为
| $ \mathit{\boldsymbol{\hat s}} = {\left( {{\mathit{\boldsymbol{H}}^{\rm{H}}}\mathit{\boldsymbol{H}} + {\sigma ^2}{\mathit{\boldsymbol{I}}_{2K}}} \right)^{ - 1}}{\mathit{\boldsymbol{H}}^{\rm{H}}}\mathit{\boldsymbol{y}} = {\mathit{\boldsymbol{W}}^{ - 1}}\mathit{\boldsymbol{\hat y}} $ | (3) |
其中:
| $ \mathit{\boldsymbol{W}} = \mathit{\boldsymbol{G}} + {\sigma ^2}{\mathit{\boldsymbol{I}}_{2K}} $ | (4) |
其中G=HHH为格拉姆矩阵. W-1的计算复杂度为O(K3), 构成了检测算法实现复杂度的主要成分.
1.2 LLR的计算首先要将估计量
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat s}}}_c} = \mathit{\boldsymbol{W}}_c^{ - 1}{\mathit{\boldsymbol{G}}_c}{\mathit{\boldsymbol{s}}_c} = \mathit{\boldsymbol{W}}_c^{ - 1}\mathit{\boldsymbol{H}}_c^{\rm{H}}{\mathit{\boldsymbol{n}}_c} = }\\ {\mathit{\boldsymbol{U}}{\mathit{\boldsymbol{s}}_c} = \mathit{\boldsymbol{W}}_c^{ - 1}\mathit{\boldsymbol{H}}_c^{\rm{H}}{\mathit{\boldsymbol{n}}_c}} \end{array} $ | (5) |
则第k个用户发送的符号估计值为
| $ {L_{k,b}} = {Y_k}\left( {\mathop {\min }\limits_{a \in \mathscr{O}_b^0} {{\left| {\frac{{{{\hat s}_{c,k}}}}{{{\mu _k}}} - a} \right|}^2} - \mathop {\min }\limits_{a' \in \mathscr{O}_b^1} {{\left| {\frac{{{{\hat s}_{c,k}}}}{{{\mu _k}}} - a'} \right|}^2}} \right) $ | (6) |
其中:系数Yk=μk2/vk2为第k个用户的信号与干扰加噪声比(SINR, signal-to-interference-plus-noise ratio),
为了降低W-1的计算复杂度, Wu等[4]提出了利用Neumann级数展开来近似获得矩阵求逆的结果.由于当基站端配备的天线数远大于单天线用户数(N≫K)时, 矩阵W具有对角占优特性[1], 即W≈D可得
| $ {\mathit{\boldsymbol{W}}^{ - 1}} = \sum\limits_{n = 0}^\infty {{{\left( { - {\mathit{\boldsymbol{D}}^{ - 1}}\mathit{\boldsymbol{E}}} \right)}^n}{\mathit{\boldsymbol{D}}^{ - 1}}} $ | (7) |
当
| $ \mathit{\boldsymbol{W}}_i^{ - 1} = \sum\limits_{n = 0}^{i - 1} {{{\left( { - {\mathit{\boldsymbol{D}}^{ - 1}}\mathit{\boldsymbol{E}}} \right)}^n}{\mathit{\boldsymbol{D}}^{ - 1}}} $ | (8) |
当i的取值较小时, Neumann级数展开能通过较低的复杂度对W-1进行近似, 但是, 当i≥3时, 其计算复杂度上升为O(K3).
Kang等[5]提出了一种改进的Neumann级数展开算法.当i=3时, 令X=D-1ED-1ED-1, 取X主对角线元素及其附近的元素构成矩阵Xd, 即
| $ \mathit{\boldsymbol{W}}_3^{ - 1} = {\mathit{\boldsymbol{D}}^{ - 1}} - {\mathit{\boldsymbol{D}}^{ - 1}}\mathit{\boldsymbol{E}}{\mathit{\boldsymbol{D}}^{ - 1}} + {\mathit{\boldsymbol{X}}_d} $ | (9) |
| $ {\mathit{\boldsymbol{X}}_d} = {\rm{diag}}\left( \mathit{\boldsymbol{X}} \right) + \sum\limits_1^T {{\rm{dia}}{{\rm{g}}_T}\left( \mathit{\boldsymbol{X}} \right)\left( {T \ge \left| {i - j} \right|} \right)} $ | (10) |
其中:diag(X)为仅保留X的对角元素并将其他所有元素置零的对角矩阵;diagT(X)为仅取与X主对角线距离为T的元素构成的矩阵, T=1, 2, 3….如此处理, 能将i=3时的Neumann级数展开算法计算复杂度降为
源于一阶泰勒级数的Newton迭代法同样可以通过迭代的方式计算W-1的近似值:
| $ \mathit{\boldsymbol{\tilde W}}_{{\rm{newton}}}^{\left( i \right)} = \mathit{\boldsymbol{\tilde W}}_{{\rm{newton}}}^{\left( {i - 1} \right)}\left( {2{\mathit{\boldsymbol{I}}_{2K}} - \mathit{\boldsymbol{W\tilde W}}_{{\rm{newton}}}^{\left( {i - 1} \right)}} \right) $ | (11) |
其收敛的充要条件为
| $ \left\| {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{W\tilde W}}_{{\rm{newton}}}^{\left( 0 \right)}} \right\| < 1 $ | (12) |
其中‖·‖表示矩阵2范数.由于矩阵W具有对角占优特性, 所以设置
| $ \left. \begin{array}{l} \mathit{\boldsymbol{\hat E}}\left( {i,j} \right) = \mathit{\boldsymbol{E}}\left( {i,j} \right),\;\;\;\;\left| {j - i} \right| \le 2\\ \mathit{\boldsymbol{\hat E}}\left( {i,j} \right) = 0,\;\;\;\;\;\left| {j - i} \right| > 2 \end{array} \right\} $ | (13) |
如此处理, 使得Neumann级数前2项可表示为
| $ \mathit{\boldsymbol{\hat W}}_2^{ - 1} = {\mathit{\boldsymbol{D}}^{ - 1}} - {\mathit{\boldsymbol{D}}^{ - 1}}\mathit{\boldsymbol{\hat E}}{\mathit{\boldsymbol{D}}^{ - 1}} $ | (14) |
令
| $ \mathit{\boldsymbol{\tilde W}}_{{\rm{newton}}}^{\left( 3 \right)} = \mathit{\boldsymbol{\hat W}}_2^{ - 1}\left( {2{\mathit{\boldsymbol{I}}_{2K}} - \mathit{\boldsymbol{W\hat W}}_2^{ - 1}} \right) $ | (15) |
由于|j-i|>2时
传统的Neumann级数展开算法在展开项数较多时其复杂度仍然会上升为O(K3), 因此, 设计一种基于Jacobi迭代的检测算法, 将Neumann级数任意展开项的复杂度降低为O(K2).
3.1 Jacobi迭代算法Jacobi迭代算法[7]用来求解形如Ax=b的N维线性方程, 将式(3) 改写为
| $ \mathit{\boldsymbol{W\hat s}} = \mathit{\boldsymbol{\hat y}} $ | (16) |
于是, 可在不对MMSE滤波矩阵W求逆的情况下估计出用户发送的信号矢量
| $ {{\mathit{\boldsymbol{\hat s}}}^{\left( i \right)}} = {\mathit{\boldsymbol{D}}^{ - 1}}\left( {\mathit{\boldsymbol{\hat y}} - \mathit{\boldsymbol{E}}{{\mathit{\boldsymbol{\hat s}}}^{\left( {i - 1} \right)}}} \right) $ | (17) |
然后将
由式(3) 可以得到对应的
| $ {{\mathit{\boldsymbol{\hat s}}}_i} = \mathit{\boldsymbol{W}}_i^{ - 1}\mathit{\boldsymbol{\hat y}} = \left( {\sum\limits_{n = 0}^{i - 1} {{{\left( { - 1} \right)}^n}{{\left( {{\mathit{\boldsymbol{D}}^{ - 1}}\mathit{\boldsymbol{E}}} \right)}^n}{\mathit{\boldsymbol{D}}^{ - 1}}} } \right)\mathit{\boldsymbol{\hat y}} $ | (18) |
用D-1代替W-1可以设置式(17) 中初始解
| $ {{\mathit{\boldsymbol{\hat s}}}^{\left( 0 \right)}} = {\mathit{\boldsymbol{D}}^{ - 1}}\mathit{\boldsymbol{\hat y}} $ | (19) |
通过计算可以得到
| $ \left. \begin{array}{l} {{\mathit{\boldsymbol{\hat s}}}^{\left( 1 \right)}} = {\mathit{\boldsymbol{D}}^{ - 1}}\left( {{\mathit{\boldsymbol{I}}_{2K}} - \mathit{\boldsymbol{E}}{\mathit{\boldsymbol{D}}^{ - 1}}} \right)\mathit{\boldsymbol{\hat y}}\\ {{\mathit{\boldsymbol{\hat s}}}_2} = \left( {{\mathit{\boldsymbol{D}}^{ - 1}} - {\mathit{\boldsymbol{D}}^{ - 1}}\mathit{\boldsymbol{E}}{\mathit{\boldsymbol{D}}^{ - 1}}} \right)\mathit{\boldsymbol{\hat y}} \end{array} \right\} $ | (20) |
则式(17) 和(18) 之间存在如下关系:
| $ {{\mathit{\boldsymbol{\hat s}}}^{\left( i \right)}} = {{\mathit{\boldsymbol{\hat s}}}_{i + 1}} $ | (21) |
通过上述理论分析, 设定式(19) 表示特殊的初始值, Jacobi迭代算法可以实现与Neumann级数展开完全相同的检测性能;同时, 在任意迭代次数下, 其计算复杂度与传统的Neumann级数展开(i≥3) 的计算复杂度相比将降低一个指数级, 保持在O(K2).由于计算LLR时需要结合W-1, 因此设计思路是, 首先计算出W-1的2阶Neumann级数展开近似值W2-1, 然后储存该变量W2-1以便在LLR计算时进行调用, 接下来对s的估计过程中执行Jacobi迭代.通过这样的方式, 在不影响s估计精度且不增加计算复杂度的情况下, 可以提高W-1估计精度, 从而有效地解决了前面绕开计算W-1之后, 又再次出现需要计算W-1的问题.
3.3 近似LLR的计算在计算第k个用户发送的第b个比特所对应的Lk, b时, 需要再次用到W-1来计算第k个用户的SINR, 这就导致前面绕开计算W-1的问题再次出现, 需要进一步处理并完善解决方案.
3.3.1 精确LLR的计算方法最为直接的办法是利用Jacobi迭代算法估计出W-1, 合并式(3) 和式(8), 令
| $ \left( {{{\mathit{\boldsymbol{\hat w}}}_{{\rm{inv}}}}} \right)_m^{\left( i \right)} = {\mathit{\boldsymbol{D}}^{ - 1}}\left( {{\mathit{\boldsymbol{e}}_m} - \mathit{\boldsymbol{E}}\left( {{{\mathit{\boldsymbol{\hat w}}}_{{\rm{inv}}}}} \right)_m^{\left( {i - 1} \right)}} \right) $ | (22) |
同样设置对角近似初始值, 令(
| $ {\left( {{{\mathit{\boldsymbol{\hat W}}}_{{\rm{inv}}}}} \right)^{\left( i \right)}} = {\mathit{\boldsymbol{D}}^{ - 1}}\left( {{\mathit{\boldsymbol{I}}_{2K}} - \mathit{\boldsymbol{E}}{{\left( {{{\mathit{\boldsymbol{\hat W}}}_{{\rm{inv}}}}} \right)}^{\left( {i - 1} \right)}}} \right) $ | (23) |
通过如此操作, 每次迭代后用(
| $ \hat \mu _k^{\left( i \right)} = \hat U_{kk}^{\left( i \right)} $ | (24) |
| $ {\left( {\hat v_k^{\left( i \right)}} \right)^2} = \sum\limits_{j \ne k}^K {{{\left| {\hat U_{jk}^{\left( i \right)}} \right|}^2} + \hat E_{kk}^{\left( i \right)}{\sigma ^2}} $ | (25) |
其中:
以上介绍了在Jacobi迭代算法下的精确LLR计算方法, 每次迭代计算(
| $ {{\tilde \mu }_k} = {{\tilde U}_{kk}} $ | (26) |
| $ \tilde v_k^2 = \sum\limits_{j \ne k}^K {{{\left| {{{\tilde U}_{jk}}} \right|}^2} + {{\hat E}_{kk}}{\sigma ^2}} $ | (27) |
其中:
基于Jacobi迭代软输出检测算法步骤如下:
输入: H, y, σ2和迭代次数i.
输出: Lk, b, (k=1, 2, …, K, b=1, 2, …, bO)
初始化:
1) G=HHH, W=G+σ2I2K,
2) W=D+E
第1次迭代: Neumann级数
3) W1-1=D-1, W2-1=D-1-D-1ED-1
4)
其他迭代: Jacobi迭代
for (n=2;n≤i; n++)do
5)
end for
LLR计算
6) W2-1→
7)
for (k=1;k≤K; k++)
8)
for (b=1;b≤1 bO; b++) do
9)
end for
end for
Return Lk, b
3.4 Jacobi迭代收敛性分析线性方程组式(16) 的精确解为
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat s}}}^{\left( i \right)}} - {{\mathit{\boldsymbol{\hat s}}}^{\left( * \right)}} = {\mathit{\boldsymbol{D}}^{ - 1}}\left( {\mathit{\boldsymbol{\hat y}} - \mathit{\boldsymbol{E}}{{\mathit{\boldsymbol{\hat s}}}^{\left( {i - 1} \right)}}} \right) - {{\mathit{\boldsymbol{\hat s}}}^{\left( * \right)}} = }\\ {{{\mathit{\boldsymbol{\hat s}}}^{\left( {i - 1} \right)}} + {\mathit{\boldsymbol{D}}^{ - 1}}\left( {\mathit{\boldsymbol{\hat y}} - \mathit{\boldsymbol{W}}{{\mathit{\boldsymbol{\hat s}}}^{\left( {i - 1} \right)}}} \right) - {{\mathit{\boldsymbol{\hat s}}}^{\left( * \right)}} = }\\ {\left( {{{\mathit{\boldsymbol{\hat s}}}^{\left( {i - 1} \right)}} - {{\mathit{\boldsymbol{\hat s}}}^{\left( * \right)}}} \right) + {\mathit{\boldsymbol{D}}^{ - 1}}\mathit{\boldsymbol{W}}\left( {{\mathit{\boldsymbol{W}}^{ - 1}}\mathit{\boldsymbol{\hat y}} - {{\mathit{\boldsymbol{\hat s}}}^{\left( {i - 1} \right)}}} \right) = }\\ {\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{D}}^{ - 1}}\mathit{\boldsymbol{W}}} \right)\left( {{{\mathit{\boldsymbol{\hat s}}}^{\left( {i - 1} \right)}} - {{\mathit{\boldsymbol{\hat s}}}^{\left( * \right)}}} \right) = }\\ {{{\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{D}}^{ - 1}}\mathit{\boldsymbol{W}}} \right)}^i}\left( {{{\mathit{\boldsymbol{\hat s}}}^{\left( 0 \right)}} - {{\mathit{\boldsymbol{\hat s}}}^{\left( * \right)}}} \right)} \end{array} $ |
令N=I-D-1W, 则有
| $ {{\mathit{\boldsymbol{\hat s}}}^{\left( i \right)}} - {{\mathit{\boldsymbol{\hat s}}}^{\left( * \right)}} = {\mathit{\boldsymbol{N}}^i}\left( {{{\mathit{\boldsymbol{\hat s}}}^{\left( 0 \right)}} - {{\mathit{\boldsymbol{\hat s}}}^{\left( * \right)}}} \right) $ | (28) |
由于在大规模MIMO系统中W为对角占优矩阵, 且D为W的对角元素, 所以N存在一个小于1的范数[7], 于是可得
| $ \mathop {\lim }\limits_{i \to \infty } {\mathit{\boldsymbol{N}}^i} = {\bf{0}} $ | (29) |
随着迭代次数i的增加,
由于所有的线性MMSE检测算法和所提出的Jacobi迭代检测算法都必须要计算滤波矩阵W=G+σ2I2K和匹配滤波信号
1) 首次迭代计算W2-1及
2) 之后执行Jacobi迭代每次迭代总共需要4K2次乘法.
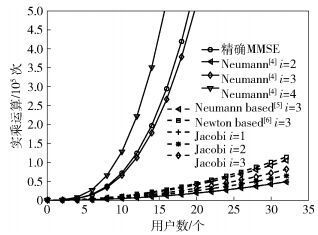
综上所述, 经过i次迭代, 总共需要4K2(i+2) -4K次乘法, 复杂度由O(K3)降为O(K2). 图 1给出了算法之间的计算复杂度对比.
|
图 1 复杂度对比 |
下面给出了基于Matlab的蒙特卡洛仿真结果.仿真实验中的传输信道为瑞利衰落信道, 卷积编码码率为1/2, 基带信号调制方式为16-QAM, 令i表示算法迭代次数及Neumann级数展开的项数.
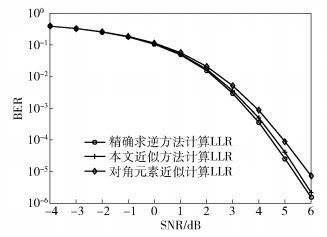
图 2对比了在使用精确MMSE估计出用户发送矢量
|
图 2 128×16MIMO配置下不同LLR计算方法性能对比 |
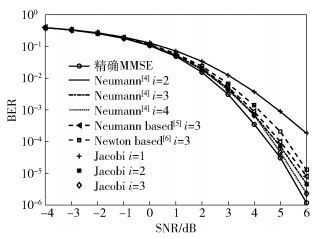
图 3给出了天线规模为128×16的MIMO系统上行链路信号检测的BER性能曲线.仿真实验中LLR的计算采用所提的近似方法. 图 3中以MMSE精确求逆算法的BER性能为基准, 对比了基于Jacobi迭代的检测算法、传统Neumann级数展开算法、Kang等[5]及Tang等[6]所提出的基于Neumann级数改进算法的检测性能.由图 3可见, 基于Jacobi迭代的检测算法在不增加复杂度的情况下经过简单的几次迭代后, 其BER性能即超过Kang等[5]和Tang等[6]所提出的基于Neumann级数展开的改进算法;同时, 在迭代次数比Neumann级数展开项数少一次的情况下实现了与后者完全一致的检测性能, 这点与3.2节理论分析完全相符, 并且在任意迭代次数下均将复杂度保持在O(K2), 而不再像后者依赖于级数展开项数.
|
图 3 BER性能对比, 128×16 MIMO配置, 16-QAM调制 |
图 4仿真天线规模为256×16的MIMO系统, 可见, 当基站天线数目与用户数的比值增大时, 仅仅依靠少量迭代次数, 基于Jacobi迭代的检测算法能够快速地向理想MMSE矩阵求逆检测算法的性能收敛, 即经过简单的几次迭代, 其检测性能就逼近最优.

|
图 4 BER性能对比, 256×16 MIMO配置, 16-QAM调制 |
基于Jacobi迭代算法, 通过设置特殊的初始值, 找到Jacobi迭代和Neumann级数展开之间的关系, 设计了一种低复杂度算法, 通过理论分析了该算法可以实现同Neumann级数展开算法相同的检测性能, 并给出了一种用于信道译码的LLR的低复杂度近似计算方法.仿真结果表明, 基于Jacobi迭代的检测算法经过较少的迭代次数就可达到接近理想MMSE矩阵求逆的检测性能, 并且将计算复杂度在不依赖迭代次数的情况下保持在O(K2), 该算法可作为大规模MIMO系统低复杂度信号检测的有效解决方案之一.
| [1] | Lu Lu, Li Geoffrey Ye, Swindlehurst A Lee, et al. An overview of massive MIMO:benefits and challenges[J]. IEEE Journal of Selected Topics in Signal Processing, 2014, 8(5): 742–758. doi: 10.1109/JSTSP.2014.2317671 |
| [2] |
汪彬, 常永宇, 权威, 等. Massive MIMO网络中低复杂度的MMSE检测方法[J]. 北京邮电大学学报, 2016, 39(6): 57–61.
Wang Bin, Chang Yongyu, Quan Wei, et al. Low-complexity MMSE detection methods for massive MIMO networks[J]. Journal of Beijing University of Posts and Telecommunications, 2016, 39(6): 57–61. |
| [3] | Qian Manli, Wang Yuanyuan, Zhou Yiqing, et al. A super base station based centralized network architecture for 5G mobile communication systems[J]. Digital Communication and Networks, 2015, 1(2): 152–159. doi: 10.1016/j.dcan.2015.02.003 |
| [4] | Wu Michael, Yin Bei, Wang Guohui, et al. Large-scale MIMO detection for 3GPP LTE:algorithms and FPGA implementations[J]. IEEE Journal of Selected Topics in Signal Processing, 2014, 8(5): 916–929. doi: 10.1109/JSTSP.2014.2313021 |
| [5] | Kang Byunggi, Yoon Ji-Hwan, Park Jongsun. Low complexity massive MIMO detection architecture based on neumann method[C]//International Soc Design Conference.[S. l.]:IEEE, 2015:293-294. |
| [6] | Tang Chuan, Liu Cang, Yuan Luechao, et al. High precision low complexity matrix inversion based on newton iteration for data detection in the massive MIMO[J]. IEEE Communications Letters, 2016, 20(3): 490–493. doi: 10.1109/LCOMM.2015.2514281 |
| [7] | Burger Martin, Kaltenbacher Barbara, Neubauer Andreas. Iterative solution methods[M]. New York: Springer, 2011: 345-384. |
| [8] | Dai Linglong, Gao Xinyu, Su Xin, et al. Low-complexity soft-output signal detection based on Gauss-Seidel method for uplink multiuser large-scale MIMO systems[J]. IEEE Transactions on Vehicular Technology, 2015, 64(10): 4839–4845. doi: 10.1109/TVT.2014.2370106 |


