在2010年, Marzetta提出了大规模多输入多输出(MIMO, multiple input multiple output)技术^[1], 该技术通过显著增加基站端天线数量, 以深度挖掘空间维度无线资源, 能更好地改善小规模MIMO的性能局限.由于大规模MIMO在能量效率、频谱效率、鲁棒性和可靠性等方面的巨大优势, 目前已成为5 G无线通信中最具潜力且最具挑战的研究方向^[2-3].众所周知, 在移动通信中, 等增益合并(EGC, equal gain combining)和最大比合并(MRC, maximal-ratio combining)接收技术是两种最常用的抗衰落技术^[4-5].当前, 已出现了很多基于MRC的大规模MIMO系统分析的论文^{[2, 6]}.可是, 相应的涉及EGC的研究结果却鲜有报道. EGC虽比MRC性能略差, 但在实际应用中具有低复杂度和低延时的特点, 因此更为经济适用^[5].

鉴于此, 本文深入研究了多小区大规模MIMO系统上行链路采用EGC的传输方案, 推导了EGC系统的可达速率, 并与MRC方案进行了比较.最后给出了仿真结果和理论分析.

下文中出现的[ ]^T和[ ]^H分别代表转置和共轭转置；[A]_mn表示矩阵A的第m行n列的元素. E{}和Var()分别代表期望函数和方差函数；I_M和0分别表示单位矩阵和0矩阵；z~$\mathscr{CN}$(0, Σ)代表均值为0, 协方差矩阵为Σ的循环对称复高斯向量z.

1 系统模型及信道估计 1.1 系统模型

假设共有L个小区, 每个小区中心配置一个具有M根天线的基站, 每个小区服务K个单天线用户, 小区间频率复用因子为1.假定l小区的K个用户向基站i发送的信号为x_l=[x_l1, x_l2, …, x_lK]^T∈C^K×1, l=1, …, L, 第i个基站接收到的信号为y_i=[y_i1, y_i2, …, y_iM]^T∈C^M×1, 第i个基站接收到的噪声为n_i=[n_i1, n_i2, …, n_iM]^T∈C^M×1, 其中n_i~$\mathscr{CN}$(0, I_M), 则第i个基站的接收信号y_i为^[2]

$ {\mathit{\boldsymbol{y}}_i} = \sum\limits_{l = 1}^L {\sqrt {{p_u}} {\mathit{\boldsymbol{G}}_{il}}{\mathit{\boldsymbol{x}}_l} + {\mathit{\boldsymbol{n}}_i}} $

(1)

假定系统用户之间是等功率发送的, 并用p_u表示用户的发射功率. g_ilkm=[G_il]_mk代表l小区的第k个用户与i小区的第m根天线之间的信道增益.因此g_ilkm可以写为

$ {g_{ilkm}} = \sqrt {{\beta _{ilk}}} {h_{ilkm}} $

(2)

其中：h_ilkm~$\mathscr{CN}$(0, 1) 代表小尺度衰落系数；β_ilk代表大尺度衰落系数；G_il的第k列元素g_ilk代表l小区的第k个用户与基站i之间的信道增益, 并服从$\mathscr{CN}$(0, β_ilkI_M)分布.在这里假设所有基站已知{β_ilk; i, l=1, …, L, k=1, …, K}, 因此式(2) 也可以表示为

$ {\mathit{\boldsymbol{G}}_{il}} = {\mathit{\boldsymbol{H}}_{il}}\mathit{\boldsymbol{D}}_{il}^{1/2} $

(3)

其中：H_il∈C^M×K为小尺度衰落矩阵且[H_il]_mk=h_ilkm, D_il∈C^K×K为大尺度衰落对角矩阵且[D_il]_kk=β_ilk.

1.2 基于导频信道估计

为了获取信道状态信息(CSI, channel state information), 需要发送上行导频来进行信道估计.在上行系统模型中用户发送长度为τ_p的导频序列, 然后基站根据用户发送的导频估计其信道.通过MMSE估计可得^{[2, 7]}

$ {{\mathit{\boldsymbol{\hat g}}}_{ilk}} = {b_{ilk}}\sum\limits_{l = 1}^L {{\mathit{\boldsymbol{g}}_{ilk}} + {\mathit{\boldsymbol{w}}_{ik}}} $

(4)

其中${b_{ilk}}\mathop = \limits^\Delta \frac{{{\beta _{ilk}}}}{{\left( {\sum\limits_{l\prime = 1}^L {} {\beta _{il\prime k}} + \frac{1}{{{\tau _p}{p_p}}}} \right)}}$且w_ik~$\mathscr{CN}$$\left( {{\bf{0}},{\rm{ }}\frac{{{b_{ilk}}^2}}{{{\tau _p}{p_p}}}{\mathit{\boldsymbol{I}}_M}} \right)$；p_p是上行导频功率, 在下文假定p_p=p_u；记g_ilk= $\mathit{\boldsymbol{\hat g}}$ _ilk+ε_ilk, 根据MMSE的特性^{[2, 7]}, 可知g_ilk的信道估计$\mathit{\boldsymbol{\hat g}}$ _ilk和其信道估计误差ε_ilk是独立的(其中$\mathit{\boldsymbol{\hat g}}$ _ilk和ε_ilk分别为信道估计矩阵$\mathit{\boldsymbol{\hat G}}$ _il与信道估计误差矩阵ε_il的第k列), 且$\mathit{\boldsymbol{\hat g}}$ _ilk~$\mathscr{CN}$(0, σ_{$\mathit{\boldsymbol{\hat g}}$ ilk}²I_M), ε_ilk~$\mathscr{CN}$(0, σ_εilk²I_M), 其中

$ \sigma _{{{\mathit{\boldsymbol{\hat g}}}_{ilk}}}^2 \buildrel \Delta \over = \frac{{\beta _{ilk}^2}}{{\sum\limits_{l' = 1}^L {{\beta _{il'k}} + \frac{1}{{{\tau _p}{p_p}}}} }} $

(5)

$ \sigma _{{\mathit{\boldsymbol{\varepsilon }}_{ilk}}}^2 \buildrel \Delta \over = \frac{{{\beta _{ilk}}\left( {\sum\limits_{l' = 1,l' \ne l}^L {{\beta _{il'k}} + \frac{1}{{{\tau _p}{p_p}}}} } \right)}}{{\sum\limits_{l' = 1}^L {{\beta _{il'k}} + \frac{1}{{{\tau _p}{p_p}}}} }} $

(6)

2 非完美CSI系统性能分析

对于多小区多用户大规模MIMO系统, 在非完美CSI的情况下, 基站通过EGC和MRC两种线性接收方法得到的信号为^[7]

$ {\mathit{\boldsymbol{r}}_i} = {\mathit{\boldsymbol{A}}^{\rm{H}}}{\mathit{\boldsymbol{y}}_i} = \sqrt {{p_u}} \sum\limits_{l = 1}^L {{\mathit{\boldsymbol{A}}^{\rm{H}}}{\mathit{\boldsymbol{G}}_{il}}{\mathit{\boldsymbol{x}}_l} + {\mathit{\boldsymbol{A}}^{\rm{H}}}{\mathit{\boldsymbol{n}}_i}} $

(7)

其中r_i∈C^K×1表示经过线性处理得到的信号, A∈C^M×K为两种线性接收方法的处理矩阵.将g_ilk= $\mathit{\boldsymbol{\hat g}}$ _ilk+ε_ilk代入式(7) 可得基站i接收到的第k个用户的信号r_ik为

$ \begin{array}{l} {r_{ik}} = \sqrt {{p_u}} \mathit{\boldsymbol{a}}_k^{\rm{H}}{{\mathit{\boldsymbol{\hat g}}}_{iik}}{x_{ik}} + \sqrt {{p_u}} \sum\limits_{j \ne k}^K {\mathit{\boldsymbol{a}}_k^{\rm{H}}{{\mathit{\boldsymbol{\hat g}}}_{iij}}{x_{ij}}} + \sqrt {{p_u}} \mathit{\boldsymbol{a}}_k^{\rm{H}}{\mathit{\boldsymbol{\varepsilon }}_{ii}}{\mathit{\boldsymbol{x}}_i} + \\ \;\;\;\;\;\;\;\sqrt {{p_u}} \sum\limits_{l \ne i}^L {\mathit{\boldsymbol{a}}_k^{\rm{H}}{{\mathit{\boldsymbol{\hat G}}}_{il}}{\mathit{\boldsymbol{x}}_l}} + \sqrt {{p_u}} \sum\limits_{l \ne i}^L {\mathit{\boldsymbol{a}}_k^{\rm{H}}{\mathit{\boldsymbol{\varepsilon }}_{il}}{\mathit{\boldsymbol{x}}_l} + \mathit{\boldsymbol{a}}_k^{\rm{H}}{\mathit{\boldsymbol{n}}_i}} \end{array} $

(8)

其中：a_k^H为A^H的第k行元素, x_ik为x_i的第k个元素.接收信号可以分为6个部分, 分别为有用信号、本小区其他用户干扰、本小区估计误差、其他小区干扰、其他小区估计误差和噪声.由于信道估计矩阵$\mathit{\boldsymbol{\hat G}}$ _il与信道估计误差矩阵ε_il在统计上相互独立, 所以i小区第k个用户的信干噪比(SINR, signal to interference plus noise ratio)为

$ {S_{ik}} = \frac{{{p_u}{{\left| {\mathit{\boldsymbol{a}}_k^{\rm{H}}{{\mathit{\boldsymbol{\hat g}}}_{iik}}} \right|}^2}}}{{\left( {{p_u}\sum\limits_{j \ne k}^K {{{\left| {\mathit{\boldsymbol{a}}_k^{\rm{H}}{{\mathit{\boldsymbol{\hat g}}}_{iij}}} \right|}^2}} + \sqrt {{p_u}} \sum\limits_{l \ne i}^L {{{\left\| {\mathit{\boldsymbol{a}}_k^{\rm{H}}{{\mathit{\boldsymbol{\hat G}}}_{il}}} \right\|}^2}} + {p_u}\mathit{\boldsymbol{a}}_k^{\rm{H}}{\mathit{\boldsymbol{R}}_\varepsilon }{\mathit{\boldsymbol{a}}_k} + {{\left\| {{\mathit{\boldsymbol{a}}_k}} \right\|}^2}} \right)}} $

(9)

其中^[7]

$ {\mathit{\boldsymbol{R}}_\varepsilon } \buildrel \Delta \over = \sum\limits_{l = 1}^L {E\left\{ {{\mathit{\boldsymbol{\varepsilon }}_{il}}\mathit{\boldsymbol{\varepsilon }}_{il}^{\rm{H}}} \right\}} = \sum\limits_{l = 1}^L {{\gamma _{il}}{\mathit{\boldsymbol{I}}_M}} $

(10)

其中：γ_il可根据ε_il的统计规律得到, 并表示为

$ {\gamma _{il}} = \sum\limits_{k = 1}^K {\sigma _{{\mathit{\boldsymbol{\varepsilon }}_{ilk}}}^2} $

(11)

通过式(9) 可得i小区第k个用户的遍历可达速率表达式为^[7]

$ {R_{ik}} = E\left\{ {{\rm{lb}}\left( {1 + {S_{ik}}} \right)} \right\} $

(12)

2.1 等增益合并接收

当基站采用EGC接收技术接收信号时, 其加权矩阵A中的元素为[A]_mk=$\frac{{{{\left[ {{{\mathit{\boldsymbol{\hat G}}}_{it}}} \right]}_{mk}}}}{{\left| {{{\left[ {{{\mathit{\boldsymbol{\hat G}}}_{it}}} \right]}_{mk}}} \right|}}$|且a_k为A的第k列.将a_k代入式(9), 即可得i小区的第k个用户的SINR_ik, 其中a_k^H $\mathit{\boldsymbol{\hat g}}$ _iik为$\mathit{\boldsymbol{\hat g}}$ _iik中每个元素的绝对值相加, 根据瑞利分布的统计特性^[4], 可得$E\{ \mathit{\boldsymbol{a}}_k^{\rm{H}}{{\mathit{\boldsymbol{\hat g}}}_{iik}}\} = M\sqrt {\frac{{\rm{ \mathsf{ π} }}}{4}\sigma _{{{\mathit{\boldsymbol{\hat g}}}_{iik}}}^2} $且${\rm{Var}}(\mathit{\boldsymbol{a}}_k^{\rm{H}}{{\mathit{\boldsymbol{\hat g}}}_{iik}}) = M\left( {1 - \frac{{\rm{ \mathsf{ π} }}}{4}} \right)\sigma _{{{\mathit{\boldsymbol{\hat g}}}_{iik}}}^2$, 所以

$ E\left\{ {{{\left| {\mathit{\boldsymbol{a}}_k^{\rm{H}}{{\mathit{\boldsymbol{\hat g}}}_{iik}}} \right|}^2}} \right\} = \left( {\frac{{{\rm{ \mathsf{ π} }}\left( {{M^2} - M} \right)}}{4} + M} \right)\sigma _{{{\mathit{\boldsymbol{\hat g}}}_{ilk}}}^2 $

(13)

通过式(4) 可得$E\{ |\mathit{\boldsymbol{a}}_k^{\rm{H}}{{\mathit{\boldsymbol{\hat g}}}_{ilk}}{|^2}\} \frac{{\beta _{ilk}^2}}{{\beta _{ilk}^2}} \times E\{ |\mathit{\boldsymbol{a}}_k^{\rm{H}}{{\mathit{\boldsymbol{\hat g}}}_{ilk}}{|^2}\} $, 并且可知‖a_k‖²=M.当j≠k时, 可知a_k^H $\mathit{\boldsymbol{\hat g}}$ _ilj为M个服从$\mathscr{CN}$(0, ${\sigma _{{{\mathit{\boldsymbol{\hat g}}}_{iij}}}^2}$)分布的独立元素相加, 因此$E\{ \mathit{\boldsymbol{a}}_k^{\rm{H}}{{\mathit{\boldsymbol{\hat g}}}_{iik}}\} $=$M\sigma _{{{\mathit{\boldsymbol{\hat g}}}_{iij}}}^2$.根据詹森(Jensen)不等式^[2], 并将上述结果代入式(12), 化简可得到EGC的遍历可达速率近似下限为

$ \begin{array}{*{20}{c}} {\tilde R_{ik}^{{\rm{EGC}}} = {\rm{lb}}\left\{ {1 + } \right.}\\ {\left. {\frac{{{p_u}\left( {\frac{{{\rm{ \mathsf{ π} }}\left( {M - 1} \right)}}{4} + 1} \right)\sigma _{{{\mathit{\boldsymbol{\hat g}}}_{ilk}}}^2}}{{\frac{{{p_u}{\rm{ \mathsf{ π} }}\left( {M - 1} \right)}}{4}\sum\limits_{l \ne i}^L {\sigma _{{{\mathit{\boldsymbol{\hat g}}}_{ilk}}}^2} + {p_u}\sum\limits_{l = 1}^L {\sum\limits_{j = 1}^K {{\beta _{ilj}}} } - {p_u}\sigma _{{{\mathit{\boldsymbol{\hat g}}}_{ilk}}}^2 + 1}}} \right\}} \end{array} $

(14)

通过式(14) 可以看出, 当固定基站天线数和用户数时, 不断增加用户发送功率并不能有效地增加传输速率, 这是由于随着发送功率的增加, 有用信号和干扰部分的功率一起增加.然而当固定用户发送功率和用户数时, 不断增加天线数, 用户的发送速率将会不断增加, 最后逐渐趋近于一定值.可以发现当发送能量${p_u} = \frac{{{E_u}}}{{\sqrt M }}$且E_u固定时, 随着天线数M趋于无穷大, 可得

$ \tilde R_{ik}^{{\rm{EGC}}} \to {\rm{lb}}\left\{ {1 + \frac{{{\rm{ \mathsf{ π} }}{\tau _p}E_u^2\beta _{iik}^2}}{{{\rm{ \mathsf{ π} }}{\tau _p}E_u^2\sum\limits_{l \ne i}^L {\beta _{ilk}^2 + 4} }}} \right\},M \to \infty $

(15)

2.2 最大比合并接收

当基站采用MRC接收时, 其加权矩阵变为A= $\mathit{\boldsymbol{\hat G}}$ _ii, 即a_k= $\mathit{\boldsymbol{\hat g}}$ _iik.可知i小区第k个用户的可达速率下限$\tilde R_{ik}^{{\rm{MRC}}}$为^[2]

$ \begin{array}{*{20}{c}} {\tilde R_{ik}^{{\rm{MRC}}} = {\rm{lb}}\left\{ {1 + } \right.}\\ {\left. {\frac{{{p_u}\left( {M - 1} \right)\sigma _{{{\mathit{\boldsymbol{\hat g}}}_{iik}}}^2}}{{{p_u}\left( {M - 1} \right)\sum\limits_{l \ne i}^L {\sigma _{{{\mathit{\boldsymbol{\hat g}}}_{ilk}}}^2} + {p_u}\sum\limits_{l = 1}^L {\sum\limits_{j \ne k}^K {{\beta _{ilj}}} } - {p_u}\sum\limits_{l = 1}^L {\sigma _{{\mathit{\boldsymbol{\varepsilon }}_{ilk}}}^2} + 1}}} \right\}} \end{array} $

(16)

3 完美CSI系统性能分析

对于完美CSI情况, 其速率表达式与非完美CSI情况类似, 不同的是完美CSI情况下其信道估计误差ε_il=0且$\mathit{\boldsymbol{\hat G}}$ _il=G_il.当采用上述两种不同接收方式时, 可得到i小区第k个用户的遍历可达速率为^[2]

$ \begin{array}{*{20}{c}} {{R_{ik}} = E\left\{ {{\rm{lb}}\left( {1 + } \right.} \right.}\\ {\left. {\left. {\frac{{{p_u}{{\left| {\mathit{\boldsymbol{a}}_k^{\rm{H}}{\mathit{\boldsymbol{g}}_{iik}}} \right|}^2}}}{{{p_u}\sum\limits_{j \ne k}^K {{{\left| {\mathit{\boldsymbol{a}}_k^{\rm{H}}{\mathit{\boldsymbol{g}}_{iij}}} \right|}^2}} + {p_u}\sum\limits_{l \ne i}^L {{{\left\| {\mathit{\boldsymbol{a}}_k^{\rm{H}}{\mathit{\boldsymbol{G}}_{il}}} \right\|}^2}} + {{\left\| {{\mathit{\boldsymbol{a}}_k}} \right\|}^2}}}} \right)} \right\}} \end{array} $

(17)

3.1 等增益合并接收

在完美CSI情况下, 采用EGC接收, 其加权矩阵A中的元素为[A]_mk=$\frac{{{{\left[ {{{\mathit{\boldsymbol{\hat G}}}_{it}}} \right]}_{mk}}}}{{\left| {{{\left[ {{{\mathit{\boldsymbol{\hat G}}}_{it}}} \right]}_{mk}}} \right|}}$且a_k为A的第k列.运用与证明式(14) 类似的方法, 可得i小区第k个用户的可达速率下限为

$ \tilde R_{ik}^{{\rm{MRC}}} = {\rm{lb}}\left\{ {1 + \frac{{{p_u}\left( {\frac{{{\rm{ \mathsf{ π} }}\left( {M - 1} \right)}}{4} + 1} \right){\beta _{iik}}}}{{{p_u}\sum\limits_{l = 1}^L {\sum\limits_{j = 1}^K {{\beta _{ilj}}} } - {p_u}{\beta _{iik}} + 1}}} \right\} $

(18)

当发送能量${p_u} = \frac{{{E_u}}}{M}$且E_u固定时, 随着天线数M趋于无穷大, 可得

$ \tilde R_{ik}^{{\rm{EGC}}} \to {\rm{lb}}\left\{ {1 + \frac{{{\rm{ \mathsf{ π} }}{E_u}{\beta _{iik}}}}{4}} \right\},M \to \infty $

(19)

3.2 最大比合并接收

在完美CSI情况下, 采用MRC接收, 其加权矩阵变为A=G_ii, 即a_k=g_iik.可得到i小区第k个用户的可达速率下限为^[2]

$ \tilde R_{ik}^{{\rm{EGC}}} = {\rm{lb}}\left\{ {1 + \frac{{{p_u}\left( {M - 1} \right){\beta _{iik}}}}{{{p_u}\sum\limits_{l = 1}^L {\sum\limits_{j = 1}^K {{\beta _{ilj}}} } - {p_u}{\beta _{iik}} + 1}}} \right\} $

(20)

通过比较式(18) 和式(20) 中的SINR, 可知$S_{ik}^{{\rm{EGC}}}/S_{ik}^{{\rm{MRC}}} = \frac{{\rm{\pi }}}{4} + \frac{1}{{M - 1}}$, 可以发现在完美CSI的情况下, 当天线数不断增加时, EGC与MRC的SINR成一定比例, 并且随着天线数的增加, EGC与MRC间的性能差距逐渐变小.

4 仿真性能与对比讨论

笔者研究的是多小区多用户大规模MIMO的经典场景, 首先介绍下本文的仿真环境：小区个数L=7；频率复用因子为1；每个小区用户数K=10；噪声功率为1；导频序列长度τ_p=10；每帧的符号长度T=196.为了方便实现, 假定β_iik=1和β_ilk=0.1, ∀l≠i, k=1, …, K.用户发送功率p_u表示为p_u=E_u/M^α, 其中E_u为固定功率, α表示功率收缩因子.定义系统频谱效率为^[2]

$ C_{{\rm{sum}}}^U = {\lambda _p}\sum\limits_{k = 1}^K {R_{ik}^U} $

(21)

其中：U∈{EGC, MRC}代表不同接收方法的标注, 在非完美CSI情况下取${\lambda _p} = 1 - \frac{{{\tau _p}}}{T}$, 完美CSI时取为λ_p=1.笔者主要仿真了在非完美和完美CSI情况下分别采用EGC和MRC这两种线性接收技术的频谱效率, 并对其性能进行了分析.

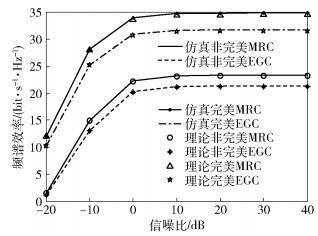
图 1在M=150和α=0对完美和非完美CSI这两种情况下, 信噪比与频谱效率之间的关系进行了仿真, 将式(14) (16) (18) 和(20) 代入式(21) 即可得到在非完美CSI和完美CSI情况下采用EGC和MRC处理方式的理论值, 将式(12) 和式(17) 代入式(21) 即可得到仿真值.通过观察可以看出闭合形式的理论结果与基于蒙特卡洛仿真得到的结果基本相匹配(由于理论结果是实际仿真结果的下限, 所以存在一定偏差)；完美CSI情况下两种接收技术的频谱效率性能要优于非完美CSI情况下的性能, 这是因为完美情况下没有信道估计误差和导频污染的影响；当基站天线数值固定时, 随着信噪比逐渐增加, EGC和MRC的频谱效率不断增加并且逐渐趋近于一定值, 尤其是在高信噪比的情况, 增加用户发送功率并不能显著提高系统频谱效率, 这与相应公式的分析结果一致, 所以在实际应用中过度提高用户发送功率不能有效改善系统性能；EGC与MRC相比, 性能略差, 但总体相差不大, 但在实际实施过程中, EGC具有硬件实现复杂度低的优势, 所以将两方面相权衡, 可以看出EGC同样是一种不错的线性处理方式.由于推导的理论结果与仿真值十分吻合, 所以在理想化假设的条件下, 在后面的仿真中采用理论值对系统性能进行分析.

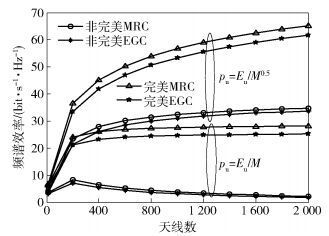
图 2在E_u=8 dB和不同的功率收缩因子下, 对完美和非完美CSI这两种情况的下频谱效率与天线数之间的关系进行了仿真.可以发现当功率收缩因子为0.5时, 对于完美CSI情况, 随着天线数的增加, 用户的频谱效率不断增加；对于非完美CSI情况, 由于导频污染的影响, 随着天线数的增加, 用户的频谱效率也不断增加, 但增幅逐渐变缓, 最后趋近于一个定值.当功率收缩因子为1时, 对于完美CSI情况, 随着天线数的增加, 用户的频谱效率不断增加, 但增幅逐渐变缓, 最后趋近于一个定值；对于非完美CSI情况, 随着天线数的增加, 用户的频谱效率先增加, 然后在一定天线数后衰减, 并逐渐趋近于0.随着天线数的不断增加, EGC和MRC的性能差距始终相差不大, 而且两者之间的差距并没有随M变大而变大, 这与理论分析一致.

5 结束语

首先介绍了上行多小区大规模MIMO的系统模型, 接着介绍了非完美CSI情况下基于导频的信道估计, 然后分别在非完美和完美CSI情况下对EGC这种接收技术进行了系统可达速率理论分析, 最后在特定系统模型和参数设置下对不同接收技术进行蒙特卡洛仿真, 并与理论结果进行对比, 验证了理论分析结果的正确性.理论分析与仿真结果表明：对于EGC这种接收技术, 完美CSI情况下的性能要优于非完美CSI情况下的性能；随着用户发送功率的增加, 频谱效率也随之增加, 但增幅逐渐变缓, 最后趋于一个定值, 因此提高发送功率不是提高频谱效率的有效方法.不同的功率收缩因子对完美和非完美CSI情况下的系统性能影响也不同, 在非完美CSI且功率收缩因子为0.5的情况和完美CSI且功率收缩因子为1的情况, 随着天线数不断增加, 系统频谱效率不断增加, 并逐渐趋近于一个定值, 说明了大规模MIMO-EGC系统也如MRC一样具有有效节约能量的特点. EGC与MRC接收技术的性能相差不大, 而EGC具有低复杂度和低延时的特点, 更为经济适用, 因此可以考虑在大规模MIMO系统中进行应用.