2. 通信网信息传输与分发技术重点实验室, 石家庄 050081
由于无线信道的复杂特性,使得无线多跳自组网在实际应用中的可靠、可用性和实时性均难以得到有效保障.对此,提出了面向时延约束下最大化带宽利用率的集中式多跳自组网络协议参数设计策略.基于无线多跳网络集中式通信调度机制,在网络参数、业务参数、协议参数的基础上充分考虑信道参数带来的影响,建立端对端时延模型和带宽利用率模型.数值仿真结果表明,集中式调度机制更适用于节点规模较小的多跳自组网络.基于上述模型增加时延约束确定网络规模,以最大化控制时隙利用率为目标设计协议参数,使网络带宽利用率在满足时延约束的前提下最优.
2. Science and Technology on Information Transmission and Dissemination in Communication Networks Laboratory, Shijiazhuang 050081, China
Wireless multi-hop ad Hoc network has been widely used in military battlefield, emergency communication and so on. However, due to the complicate characteristics of wireless channel, it is difficult to obtain reliable protection and real-time reliability in practice. A design strategy on protocol parameters for centralized multi-hop ad Hoc network was proposed to maximize the bandwidth utilization under delay constraint. Based on centralized wireless multi-hop ad Hoc network communication mechanism, an end-to-end delay model and a bandwidth utilization model were established, which fully consider the impacts of four aspects of parameters, network, traffic, protocol and channel. It is shown that the centralized scheduling mechanism is more suitable for the smaller network. Finally, an optimization strategy was given to properly design protocol parameters in different network scenarios under delay constraint.
IEEE 802.16中明确提出无线自组网的2种调度模式:集中式和分布式[1].其中, 相比于分布式调度, 集中式调度模式具有控制稳定、冲突小、性能易把控等特点, 在工业控制领域应用更为广泛.
目前国内外学者针对集中式自组网方面的研究多集中在第3代、第4代移动通信网络以及802.11宽带接入网络等单跳无线网络在不同应用场景下的网络性能和优化等方面, 并取得了大量研究成果[2-4].在长期演进技术升级和第5代移动通信中引入中继技术和设备到设备技术的空口两跳通信, 其涉及的标准和关键技术也是目前研究的热点[5-6].在IEEE 802.11s/IEEE 802.16/IEEE 802.15标准中对集中式多跳自组网络的相关机制进行了完善, 但综合考虑业务实时性需求并指导协议设计的研究相对较少[7].
李旭等[8]从网络参数、业务参数2个方面进行了较为全面的分析, 但未充分考虑信令长度、信道质量等参数的影响.笔者在此基础上结合工程应用充分考虑信道参数带来的影响, 建立端对端时延模型和带宽利用率模型, 考虑业务时延约束设计协议参数, 最后对该设计策略进行分析验证.
1 集中式多跳自组网络通信机制分析集中式多跳网络由基站和用户站节点组成, 构成以基站为根节点的调度树状结构, 如图 1所示.
|
图 1 集中式多跳网络调度树结构 |
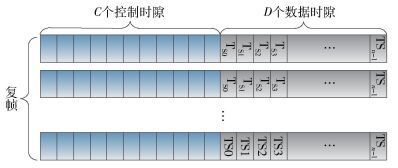
网络采用如图 2所示的帧结构, 多个复帧构成一个调度周期, 在一个调度周期内所有节点通过集中式调度配置(CSCF, centralized schedule configuration)消息、集中式调度申请(CSCR, centralized schedule request)消息、集中式调度授权(CSCG, centralized schedule grant)消息3种集中式调度消息完成网络维护、资源调度以及数据通信.
|
图 2 集中式多跳网络帧结构 |
在集中式多跳自组网络中, 一次完整的调度流程包括3部分:① 所有节点的业务请求都通过CSCR消息汇集到基站;② 基站根据网络拓扑为网络中所有业务寻找最佳路由, 并通过资源复用等技术实现合理的资源分配;③ 基站将分配结果通过CSCG消息广播全网进行授权.此外, 基站需要周期性广播CSCF消息来维护调度树结构.通过上述流程, 最终所有节点按照统一调度结果进行数据传输, 从而实现无碰撞、资源利用最大化的数据通信调度.
2 网络性能建模在集中式多跳自组网络中, 集中式调度消息的非成功传输将导致子树上所有节点分配的数据时隙浪费, 进而导致业务传输时延增大, 同时使得系统有效带宽利用率降低.考虑上述影响, 将基于下列4类参数分别建立端对端时延模型和带宽利用率模型.
1) 网络参数:网络规模N, 节点距基站最大跳数H, 网络总带宽W;
2) 信道参数:链路出错概率pe;
3) 业务参数:单节点业务占时隙数λ;
4) 协议参数:一个调度周期控制时隙个数为C, 数据时隙个数为D, 一个时隙长度ΔB.
在下面的模型中, 设定链路质量在一个调度周期内是不变的, 一个调度周期内的控制时隙是连续的, 且节点间的收发消息是瞬时的, 即忽略处理时延和传输时延.其中, 各消息时隙块所包含的时隙个数分别为
| $\left. \begin{align} & {{s}_{\text{CSCF}}}=31+4N \\ & {{s}_{\text{CSCR}}}=\frac{\left( 13H+63 \right)\left( N-1 \right)}{2N} \\ & {{s}_{\text{CSCG}}}=33+5\left( N-1 \right)\left( 1+H \right) \\ \end{align} \right\}$ | (1) |
基于前文描述的集中式调度通信机制, 业务的一次完整调度示意图如图 3所示.在分析中认为业务数据包从应用层到数据链路层为尽最大努力交付, 即在数据链路层以上队列满时则丢包, 故可将数据包从应用层到数据链路层的时间均值视为一定值, 且不受上述4类参数的影响, 因此所分析的业务端对端时延实际为业务包从源节点数据链路层到目的节点数据链路层的时延, 由4部分组成, 即业务申请等待时延t1~t2、业务调度时延t2~t3、业务发送等待时延t3~t4和传输时延t4~t5.其中t4~t5段为数据包在信道中的传输时延, 由于相比其他3段时延很小, 故忽略不计.下面分别对前3段时延进行计算分析.

|
图 3 集中式多跳网络调度流程 |
业务申请等待时延T12指业务流到达数据链路层到节点发送CSCR消息申请数据时隙的时间.假设上层的业务流到达数据链路层服从泊松过程, 在一个调度周期中业务到达时刻取值范围为1~(C+D), 服从均匀分布.在一个调度周期的CSCR传输时隙中, 每个节点只有一次相对固定传输机会, 一旦错失, 就需要等到下一调度周期.则
| $E({{T}_{12}})=\sum\limits_{t=1}^{C+D}{{}}\frac{t}{C+D}=\frac{1+C+D}{2}$ | (2) |
业务调度时延T23可分为2段:① 该节点发送CSCR消息到基站接收到全网节点的CSCR消息Tr(i);② 基站接收到全网节点CSCR消息到全网节点都接收到CSCG消息Tg(i).考虑到链路存在出错的情况, 故一次完整的成功请求并授权的时间可能需要跨越多个调度周期, 故节点i申请成功所需的申请次数服从几何分布, 期望值为(1-pe)-2H(i), 此时有
| ${{T}_{23}}\left( i \right)={{T}_{\text{r}}}\left( i \right)+{{T}_{\text{g}}}\left( i \right)+[{{(1-{{p}_{\text{e}}})}^{-2H(i)}}-1]\left( C+D \right)$ | (3) |
由图 3中分析可知, 节点i发送CSCR消息到基站接收到全网节点的CSCR消息时间为
| ${{T}_{\rm{r}}}\left( i \right)=~\left\lceil \frac{{{\mathit{s}}_{\rm{CSCR}}}}{\mathit{\Delta }} \right\rceil \frac{~C+D}{C}i$ | (4) |
同理, 有
| ${{T}_{\rm{g}}}\left( i \right)=\left\lceil ~\frac{{{s}_{\rm{CSCG}}}}{\mathit{\Delta }} \right\rceil \frac{~C+D}{C}N$ | (5) |
业务发送等待时延T34指节点在接收CSCG消息后到业务发送出去所需时间, 由于全网节点的业务需在一个调度周期内完成, 所以T34的期望值为
| $E({{T}_{34}})=\frac{C+D}{2}$ | (6) |
在不考虑传输时延的前提下, 端对端时延Te2e=T12+T23+T34, 将式(2) ~式(6) 代入可得
| $\eqalign{ & {T_{{\rm{e2e}}}} = \{ \frac{1}{2} + C + D + N\left\lceil {\frac{{{\mathit{s}_{{\rm{CSCR}}}}}}{\mathit{\Delta }}} \right\rceil + \cr & N\left\lceil {\frac{{{s_{{\rm{CSCG}}}}}}{\mathit{\Delta }}} \right\rceil \frac{{C + D}}{C} + {\rm{ }}\frac{{\left( {C + D} \right)}}{{{{\left( {1 - {p_{\rm{e}}}} \right)}^{2H}}}}\} \frac{{8\Delta }}{W} \cr} $ | (7) |
系统带宽利用率定义为一个调度周期内网络中所有数据业务在网络总消耗的占比.设网络中所有子节点均有一条发往中心节点的业务, 按照资源均分的原则, 一个调度周期内所有业务需要的数据时隙个数表示为
| $\frac{{\lambda \left( {N - 1} \right)}}{H}\sum\limits_{i = 1}^H {} i = \frac{{\lambda \left( {N - 1} \right)\left( {1 + H} \right)}}{2}$ | (8) |
考虑链路质量的因素, 则网络带宽利用率为
| $\begin{array}{c} \eta = \\ \frac{{\lambda \left( {N - 1} \right)\left( {1 + H} \right){{(1 - {p_{\rm{e}}})}^{2H}}}}{{2\left[ {N\left\lceil {\frac{{{s_{{\rm{CSCF}}}}}}{\mathit{\Delta }}} \right\rceil + N\left\lceil {\frac{{{\mathit{s}_{{\rm{CSCR}}}}}}{\mathit{\Delta }}} \right\rceil + N\left\lceil {\frac{{{s_{{\rm{CSCG}}}}}}{\mathit{\Delta }}} \right\rceil } \right] + \lambda \left( {N - 1} \right)\left( {1 + H} \right)}} \end{array}$ | (9) |
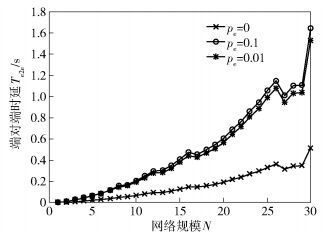
1) 不同链路质量下端对端时延与网络规模的关系
设定网络拓扑为互连互通网状网络, λ=2, W=10 Mbit/s, 如图 4所示, 随着N值的增加, Te2e整体呈上升趋势, 这是由于N增加导致各调度消息长度增加和业务需求增多, 进而导致调度周期拉长和端对端时延增加.曲线中的拐点是由于在计算过程中为更符合实际场景对时隙取整而造成的.稳态环境下和非稳态环境下端对端时延曲线差异较大, 这是由于在链路不稳时, 存在丢包、错包现象, 要完成一次完整的调度需要多个调度周期, 进而导致Te2e的增加.
|
图 4 不同链路质量场景网络规模与端对端时延的关系 |
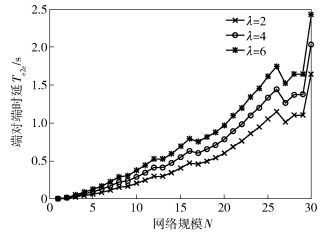
2) 不同业务参数下端对端时延与网络规模的关系
网络拓扑和带宽设置同1), pe=0.01, 如图 5所示, 同一网络规模下, 随着λ增大, 整个网络的业务需求量迅速膨胀, Te2e稳步上升, 一种方法是通过多个调度周期去完成全网业务调度, 另一种方法是通过拉长调度周期使得在一个调度周期完成全网业务调度, 但是两者都会带来Te2e的明显增大.
|
图 5 不同业务参数场景网络规模与端对端时延的关系 |
1) 典型网络拓扑中带宽利用率与网络规模的关系
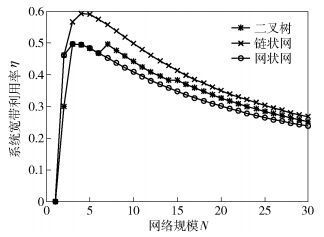
设置λ=2, 如图 6所示, 不同网络拓扑中同一网络规模时, 链状网络拓扑下η最高, 这是因为在网络中所有节点均有到中心节点的业务时, 链状网络拓扑中节点利用数据时隙个数最多, 而网状拓扑利用的最少;同时可以看出, 各网络拓扑对应η最大的网络规模分别为链状网络N(ηmax)=4, 二叉树网络N(ηmax)=7, 网状网络N(ηmax )=3.
|
图 6 不同网络拓扑场景网络规模与带宽利用率的关系 |
2) 不同业务参数下带宽利用率与网络规模的关系
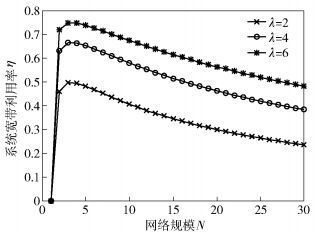
设置网络拓扑为互连互通网状拓扑, 如图 7所示, 随着λ增大, η明显增大, 这是因为λ增大只是数据量的增大, 但业务条数并未增多, 因此相同的控制开销下能够调度的数据量显著增大, 所以η有明显增加, 但从图 5结论中可知与此同时Te2e也明显增大, 因此若采用增大λ的方式来提高η还需要考虑Te2e不能过大, 否则会影响业务实时性.
|
图 7 不同业务参数场景网络规模与带宽利用率的关系 |
设定当前应用场景为W=10 Mbit/s, pe=0.01, λ=4, 网络结构为互连互通网状网, 如图 8所示, 临界点A为在端对端时延约束Te2e-max=1 s时, 满足该约束下的网络规模临界取值, 可以看出N=20.8, 即在N≤20的网络下均可以保证端对端时延在约束范围内.

|
图 8 时延约束下选择合适N值 |
为进一步描述设计策略, 定义控制时隙利用率αC为所有调度消息对控制时隙的利用情况:
| ${\alpha _{\rm{C}}} = \frac{{{s_{{\rm{CSCF}}}} + {s_{{\rm{CSCR}}}} + {s_{{\rm{CSCG}}}}}}{{\left( {s\left\lceil {\frac{{{s_{{\rm{CSCF}}}}}}{\mathit{\Delta }}} \right\rceil + s\left\lceil {\frac{{{\mathit{s}_{{\rm{CSCR}}}}}}{\mathit{\Delta }}} \right\rceil + s\left\lceil {\frac{{{s_{{\rm{CSCG}}}}}}{\mathit{\Delta }}} \right\rceil } \right)\mathit{\Delta }}}$ | (10) |
通过设计Δ最大化αC, 避免控制时隙资源不必要的浪费.由式(10) 得到的不同网络规模下对应的最佳Δ值, 如图 9所示.

|
图 9 N与最佳Δ取值关系 |
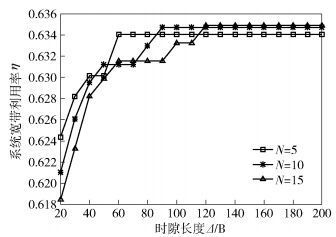
现基于Matlab搭建物理层信道模型, 使信道状态满足pe=0.01, 采用NS2仿真平台对集中式多跳自组网络通信机制进行仿真分析.仿真过程中网络规模N分别取5、10、15, Δ以10为步进从20~200分别取值, 得到不同场景下的网络带宽利用率, 如图 10所示.
|
图 10 不同N和Δ取值下的带宽利用率 |
在N取不同值时, 仿真最佳Δ为对应带宽利用率最大时的最小取值, 与图 9所得不同N值时的最佳Δ比较结果如表 1所示.
|
|
表 1 不同场景下理论与仿真最佳Δ比较 |
由表 1可以看出, 在Δ以10为步进时仿真得到的最佳Δ与数值计算得出的最佳Δ基本相符, 因此根据此策略进行协议参数设计可以保证在端对端时延满足时延约束的前提下最大化带宽利用率.
4 结束语网络规模、业务需求、信道质量、协议参数都是影响网络性能的重要参数, 笔者在定量分析各参数对系统带宽利用率和端对端时延的影响之后, 考虑端对端时延约束, 给出以最大化控制时隙利用率为目标设计协议参数的策略, 以保证系统性能达到最优.此外, 数值仿真结果表明了集中式调度机制更适合节点规模较小的多跳无线自组网络.在实际应用中可通过采用分级组网的形式来扩大网络规模, 与此同时还保留了集中式多跳无线自组网的易控制、系统稳定可靠等优势.本研究成果能够很好地指导实际工程应用中协议参数的合理设计, 并为后续网络规模扩大后的分级组网机制设计以及协议参数设计奠定理论基础.
| [1] | Kas M, Yargicoglu B, Korpeoglu I, et al. A survey on scheduling in IEEE 802.16 mesh mode[J]. IEEE Communications Surveys & Tutorials, 2010, 12(2): 205–221. |
| [2] | Lin Yibing, Lin Pinjen, Sung Y C, et al. Performance measurements of TD-LTE, WiMax and 3G systems[J]. IEEE Wireless Communications, 2013, 20(3): 153–160. doi: 10.1109/MWC.2013.6549295 |
| [3] | Liao Ruizhi, Bellalta B, Oliver M, et al. MU-MIMO MAC protocols for wireless local area networks:a survey[J]. IEEE Communications Surveys & Tutorials, 2016, 18(1): 162–183. |
| [4] | Trabelsi N, Chen Chungshue, Azouzi R E, et al. User association and resource allocation optimization in LTE cellular networks[J]. IEEE Transactions on Network and Service Management, 2017, 14(2): 429–440. doi: 10.1109/TNSM.2017.2677778 |
| [5] | Mafuta A D, Walingo T, Ngatched T M N. Energy efficient coverage extension relay node placement in LTE-A networks[J]. IEEE Communications Letters, 2017, 21(7): 1617–1620. doi: 10.1109/LCOMM.2017.2691344 |
| [6] | Cheng Yulun, Yang Longxiang, Zhu Hongbo. Operator profit-aware wireless virtualization for device-to-device communications underlaying LTE networks[J]. IEEE Access, 2017, 5: 11668–11676. doi: 10.1109/ACCESS.2017.2715813 |
| [7] | Song Wenzhan, Huang Renjie, Shirazi B, et al. TreeMAC:localized TDMA MAC protocol for real-time high-data-rate sensor networks[C]//IEEE International Conference on Pervasive Computing and Communications. Galveston, Texas, USA:IEEE Computer Society, 2009:1-10. |
| [8] |
李旭, 董猛, 刘颖. 集中式多跳调度系统性能建模与协议参数优化[J]. 北京邮电大学学报, 2016, 39(2): 108–112.
Li Xu, Dong Meng, Liu Ying. Performance modeling and protocol parameters optimization for centralized multi-hop scheduling systems[J]. Journal of Beijing University of Posts and Telecommunications, 2016, 39(2): 108–112. |
| [9] | 李富艳. 无线Mesh网络分布式与集中式资源调度关键技术研究[D]. 北京: 北京交通大学, 2012. |


