针对盲信号处理中一种极端的病态混叠情况,单通道盲源分离是一个近年受到广泛关注的重要研究方向,并且具有广泛的应用前景.首先阐述了单通道盲源分离的数学模型、可分离性分析和分离效果评价标准,然后在深入研究单通道盲源分离发展的基础上分类讨论和评估了一些现有的单通道盲源分离方法,在介绍各方法的基本原理、特征及应用的同时,指出当前单通道盲源分离技术所面临的问题与挑战.最后结合当前的研究状况对单通道盲源分离未来的发展及研究方向进行了分析.
As a case of ill-conditioned signal mixing, the single channel blind source separation (SCBSS) is an important research field which has been widely given attention and has broad application prospects. The mathematical model of SCBSS and the evaluation index of separation effect are described firstly. Secondly, on the basis of an in-depth investigation into latest development of SCBSS, some kinds of existing theories and methods are then emphatically discussed and summarized, then the applications of the methods presented are systematically explained. Finally the challenges and prospects for further development in the area are listed.
盲源分离[1]是指在源信号的先验信息和信道传输参数均未知的情况下, 仅利用传感器接收到的观测信号来恢复出源信号的过程.这里“盲”有两重含义:其一是信源的统计分布特性未知, 其二是信道的混合系数未知.关于盲源分离技术的研究已成为国际上信号处理领域的一个热点, 并且已经被广泛应用于数字通信、图像处理、生物医学、语音信号处理等领域.根据源信号数目和观测信号数目的关系, 可以将盲源分离分为超定盲源分离(观测信号数目大于源信号数目)、适定盲源分离(观测信号数目等于源信号数目)和欠定盲源分离(观测信号数目小于源信号数目)三类.其中, 单通道盲源分离是欠定盲源分离的一种极端情况.单通道盲源分离[2] (SCBSS, single channel blind source separation)是指利用单个接收传感器来接收观测信号, 并且只利用这一路观测信号来恢复出各个源信号的过程.单通道盲源分离需要利用较少的量去估计较多的量, 这是一个病态的问题, 解决起来极其困难.与具有两路以上观测信号的欠定盲源分离相比, 单路观测信号的盲分离在处理方法上已经发生了本质的变化, 因为基于矩阵表示的数学模型和相应的分析方法已不再适用.对于单通道盲源分离技术的研究, 需要在信号展开、滤波或者借助其它理论工具等方向上探索解决这一问题.由于单通道盲源分离可供直接利用的信息较少, 需要充分挖掘并利用信号的不同潜在特性, 包括信号的时域特性、频域特性以及统计特性等, 目前利用信号的这些潜在特性来解决单通道盲分离问题的理论研究与发展还尚未成熟.与适定或超定盲源分离技术相比, 单通道盲源分离技术所需要的硬件设备大幅度减少, 系统成本大为降低, 具有重要的实际研究意义和广阔的应用前景.
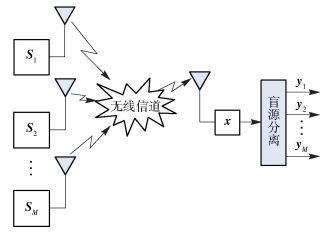
1 单通道盲源分离的数学模型单通道盲源分离的主要过程如图 1所示.
|
图 1 单通道盲分离过程 |
假设单个接收传感器在离散采样时刻t接收到的观测信号x(t)是由M路源信号s(t)=[s1(t), s2(t), …, sM(t)]T通过线性瞬时混合得到, 则单通道盲源分离的数学模型可以表示为
| $x\left( t \right) = \sum\limits_{i = 1}^M {} {a_i}{s_i}\left( t \right) + n\left( t \right)$ | (1) |
或等价为
| $x\left( t \right) = {\mathit{\boldsymbol{a}}^{\rm{T}}}\mathit{\boldsymbol{s}}\left( t \right) + n\left( t \right)$ | (2) |
其中:si为第i路源信号, t=1, 2, …, T表示采样时刻, a=[a1, a2, …, aM]T为混合系数向量, n(t)为高斯白噪声.
单通道盲源分离需要解决的问题是在混合系数向量aT和源信号未知的情况下, 如何通过挖掘和利用接收信号的不同特征, 使用相应的算法对接收信号进行处理, 并分离出各个源信号.
2 单通道混合信号的可分离性和分离效果评价标准建立盲源分离的数学模型和进行可分离性分析, 是研究单通道盲源分离首先要考虑的问题, 同时建立相应的分离效果评价指标也非常重要.
首先, 如何保证从单通道混合信号中分离出来的源信号具有唯一性, 这就涉及单通道混合信号的可分离性问题.解决盲源分离问题的关键在于如何挖掘和利用所针对问题的潜在先验知识.从本质上来说, 现今的单通道盲源分离算法, 都是利用信号之间的差异性来进行分离的.只要信号在某些域如时域、频域、码域或其他变换域存在足够的差异性, 就能实现信号的盲源分离. Cohen等[3]通过时频分析定义了信号分量的瞬时频率和瞬时带宽, 并提出多分量混合信号的可分离性是由各信号分量的瞬时频率和瞬时带宽所共同决定的, 只要各个信号分量在时频域上是可分离的, 则多分量混合信号就可以实现分离.剑桥大学Hopgood J.R和Rayner P.J.W[4]将上述结论进一步推广, 得出多分量混合信号若能够分离, 则各信号分量必须在某个域是可分离的.此外, 文献[5-6]中对实现盲源分离所需要的条件也做了详细的论述.
其次是分离效果的评价标准, 单通道盲源分离算法从接收到的单路混合信号中恢复出各个源信号, 通常用源信号估计值与真实值对比来评价算法的性能.常用的评价准则有以下几类[7-8].
2.1 相似系数假设分离出的信号ym=[ym(1), ym(2), …, ym(T)]是对应第m路源信号的一个估计, t=1, 2, …, T表示不同的采样时刻, 且假设实际的源信号为sm=[sm(1), sm(2), …, sm(T)], 则估计信号与实际源信号间的相似系数可作为分离性能的一个度量.其中, 相似系数定义为
| $\rho = \sum\limits_{m = 1}^M {} \frac{{\left| {\sum\limits_{t = 1}^T {} {y_m}\left( t \right){s_m}\left( t \right)} \right|}}{{\sqrt {\sum\limits_{t = 1}^T {} {y_m}^2\left( t \right)\sum\limits_{t = 1}^T {} {s_m}^2\left( t \right)} }}$ | (3) |
其中:M为源信号个数, 且0 < ρ < 1, ρ越大意味着估计的源信号的波形越接近实际源信号, 即分离算法的分离效果越好, 反之, 算法分离效果越差.
2.2 输出信噪比输出信噪比也是盲分离性能的一个度量标准, 假设ym(t)是对第m路源信号的估计, 实际的源信号为sm(t), 则输出信噪比的计算公式为
| ${R_m} = 10\log \left( {\frac{{\sum\limits_{t = 1}^T {} {s_m}^2\left( t \right)}}{{\sum\limits_{t = 1}^T {} {{[{y_m}\left( t \right) - {s_m}\left( t \right)]}^2}}}} \right)$ | (4) |
Rm越大, 则表示盲源分离效果越好.
2.3 输出误码率对于数字通信而言, 信号的有用信息存储在码元序列中, 盲源分离算法只需要估计出源信号的码元序列即可, 而不需要将源信号的整个波形估计出来, 因此可以将估计的码元符号与原始发送的码元符号进行比较, 得到输出信号误码率(SER, symbol error rate)为
| $R = \frac{{{N_{\rm{e}}}}}{N}$ | (5) |
其中:Ne为估计错误的码元数目, N为信源发送的所有码元个数.误码率越低, 盲分离算法的分离性能越好.
对于不同的源信号类型或不同的分离算法, 需要选定不同的评价标准, 这有助于分析算法的优劣, 并直接影响盲源分离算法的分析与研究.
3 单通道盲源分离算法的研究进展由于单通道盲源分离问题比较特殊, 分离算法一般会依赖于源信号本身的一些特性, 目前还没有一种算法可以解决任何情况下的单通道盲源分离问题.针对单通道盲源分离算法的研究, 国内外已有许多学者做了大量奠基性的工作, 并提出了相应的分离算法, 现归类总结如下.
3.1 将单通道转换为多通道的方法Jutten和Herauh等[9]首次提出了盲源分离的概念, 经过20多年的发展, 多通道盲源分离的理论已经相对成熟.因此, 已有不少学者在对单通道盲源分离算法进行研究时, 尝试将单通道问题转换为多通道的问题, 然后再利用多通道盲源分离方法进行求解.
文献[10]中将塔肯斯定理(Takens theory)和C-C方法构造多维映射的思想引入单通道盲分离算法中, 通过计算接收信号的时间延迟参数和重构的嵌入维数, 将单通道混合信号映射成多维的虚拟观测信号, 然后将有限支持样本方法(FSS-Kernel Function, finite support sample kernel function)的思想与传统的快速独立成分分析(Fast-ICA, fast independent component analysis)方法相结合, 实现各路源信号的分离.
根据经验模式分解(EMD, empirical mode decomposition)方法具有将一维信号分解为多路固有模态函数(IMF, intrinsic mode function)的增维特性, 许多文献[11-13]中将其作为伪多输入多输出(MIMO, multiple Input multiple output)映射预处理模块, 应用到单通道盲分离算法当中, 使得多通道盲源分离算法也能够在欠定场景下使用.经验模式分解法的目的在于通过对原始的混合信号进行分解, 从而得到一组线性平稳且具有实际物理意义的固有模态函数.其中, EMD算法的基本分解过程如下:
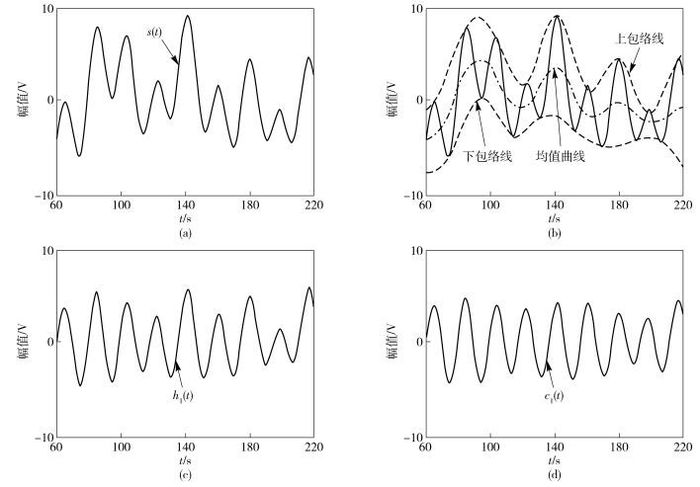
1) 找出信号序列s(t)中的所有极大值点和极小值点, 将其用三次样条函数分别拟合为序列的上包络和下包络线, 并求出其平均值m(t).
2) 计算筛选分量h1(t), 其中h1(t)=s(t)-m(t), 筛选过程如图 2(b)(c)所示.
|
图 2 EMD分解过程 |
3) 将h1(t)作为一个新序列, 重复步骤1) 和步骤2), 直到h1(t)满足IMF的条件, 此时将h1(t)作为第一个IMF, 记做c1(t), 如图 2(d)所示.
4) 用原始混合信号s(t)减去c1(t), 得到残余函数r1(t), 即:r1(t)=s(t)-c1(t).
5) 将残余函数r1(t)作为一个新序列, 重复以上第1) 步骤到第4) 步骤, 便可得到第2、第3以至第n个IMF函数, 直到rn(t)变为一个单调序列或只有一个峰值点.此时, 原始信号序列可表示为各个IMF分量和残余分量的和, 即
根据EMD分解原理, 文献[14]中针对传统盲源分离算法无法在单路接收的跳频通信场景中使用的问题, 将单路的接收跳频信号进行增维处理, 转化为多路虚拟观测信号, 然后分别使用全盲盲源分离和半盲盲源分离算法实现干扰信号和源信号的分离, 验证了方法的有效性.
在构造多通道的方法中, 另一类思想是根据小波理论, 将单通道接收信号进行小波或小波包分解, 构造多路虚拟观测信号, 然后结合传统的超定盲分离算法估计出源信号[15-16].在此类方法中, 小波基的合适选取将直接影响到算法的分离效果.
3.2 变换域滤波方法在信号处理早期阶段, 研究者发现时域重叠的多通道数据通过Fourier变换、离散余弦变换(DCT, discrete cosine transformation)域维纳滤波、循环谱变换以及脉冲相关自适应滤波器[17-19], 就可以在这些谱域上将重叠信号分离开来. Hopgood J.R等在这方面开展了大量的工作, 不仅回答了混合信号的可分离性问题, 而且给出了构造混合信号可分离变换域的方法, 拓宽了传统时域、频域和空域滤波的思想, 开拓了单通道盲源分离算法的研究思路.
文献[20]中根据单通道时频重叠调制信号在循环谱域具有独立性和稀疏性的特点, 进一步提出通过循环谱域滤波器来实现两路源信号分离的算法, 该算法采用周期图法对一调制信号进行循环谱估计, 得到该调制信号中具有最强谱相关特性的循环频率点, 再将该频率点作为线性共轭线性频移(LCL-FRESH, linear conjugate linear frequency shift)滤波器的频移量从单通道时频重叠信号中提取出具有该循环频率的调制信号.然而, 现实的使用环境越来越复杂, 使单通道时频混叠信号变得普遍存在.因此, 需要进一步研究如何在频谱发生混叠的情况下, 对通信信号实现单通道盲信号分离.
文献[21]中给出了一种基于希尔伯特黄变换(HHT, Hilbert-Huang transform)和独立分量分析(ICA, independent component analysis)的单通道通信信号盲源分离算法, 算法中首先对单通道混合通信信号进行HHT变换, 得到混合信号的边际谱, 然后通过边际谱估计出源信号数目, 根据源信号数目以及本征模态函数重组多通道混合通信信号, 并通过ICA算法来恢复出源信号.该方法能够实现源信号为两路通信信号时的盲分离, 但源信号数目较多时, 将无法构造足够的输入矩阵, 此时如何实现源信号的分离需要进一步研究.
针对直扩信号和干扰信号在时频域严重交叠的情况, 文献[22]中基于变换域滤波的思想, 利用直扩信号和干扰的二阶循环平稳差异, 从含有强干扰的业务混合信号频移向量中分离出期望的通信信号, 从而提升直扩通信在强干扰下的抗干扰能力, 但算法中需要知道直扩信号的部分先验信息, 生成训练序列, 并非真正意义上的全盲.
3.3 稀疏分解表示方法对信号进行稀疏处理是解决欠定盲源分离的一种有效手段, 是当前解决欠定问题的研究热点之一.稀疏化处理的基本方法是采用时频线性变换对欠定多路信号进行稀疏处理, 然后通过聚类的方法实现对混合矩阵的估计, 在最大后验概率准则下实现分离[23-26].
2006年, Cédric Févotte等[27]根据在一组给定基下具有稀疏表示的线性瞬时混合信号, 提出了一种基于Bayesian的盲源分离算法, 该算法将给定基下的源信号的系数分布建模为Student分布, 此分布可表示为Gaussian型标量混合, 由此即可估计出混合矩阵和源信号.
Smith等[28]根据生物听觉神经处理信息的原理, 提出一种基于稀疏编码(Spike-Coding)的方法将单通道信号表示为多个基与源信号对应系数的卷积形式, 并利用匹配追踪算法自适应地计算出基与系数, 从而得到源信号的稀疏表达形式.这一方法被发表于《Nature》杂志以来, 因其所需人工经验少、抗噪能力强、自适应性好等优点, 得到了广泛的关注.
根据传统稀疏分解理论, 单通道信号y∈Rn可以表示成一个过完备字典D=[d1, d2, …, dk]∈Rn×k中的所有基的线性组合, 即y=Dβ+n, 其中n为白噪声向量, 向量β=[β1, β2, …, βk]为源信号的稀疏系数向量.而在Smith等人提出的Spike-Coding编码方法中, 将单通道信号看成基与系数的卷积
| $\mathit{\boldsymbol{y}} = \sum\limits_{j = 1}^k {} {\mathit{\boldsymbol{d}}_j}*\mathit{\boldsymbol{\beta }} + \mathit{\boldsymbol{n}}$ | (6) |
在恒定的工作状况下, 不同源信号具有不同的特征, 同一源信号具有类似的特征.在Spike-Coding编码方法中, 可以把不同的基与对应系数的卷积(dj*β)看作一个源信号或者源信号的一部分. dj和β都是未知的, 无法同时对它们进行求解, 但可以利用最大后验概率方法将该问题转化为系数求解和字典学习两个过程, 反复迭代, 直到收敛或满足迭代停止条件.
在Smith等所做工作的基础上, 文献[29]中针对特征反复出现的机械信号, 提出一种基于移不变稀疏编码的单通道盲源分离方法.算法中将源信号看成多个基与系数的卷积, 能够根据信号的统计分布, 利用信号自身特征自适应地学习到匹配的基和稀疏的系数.该方法所需人工经验少、鲁棒性好, 适用于单通道机械信号盲源分离, 而对于其他类型的源信号, 如通信信号, 语音信号的适用性有待进一步验证.
3.4 多参数联合估计方法对于单通道盲源分离问题, 由于获得的信息量极少, 需要从仅有的一路混合信号中充分挖掘出可用信息, 必要时需要由混合信号来估计源信号的参数, 如码速率和载频等, 从而利用估计出的参数作为先验信息为信号的分离服务, 因此有必要研究单通道情况下信号参数估计方法.
文献[30]中针对渐近信号在连续小波变换平面上显示出明显的脊, 并且脊上的信息与源信号相比有最大的相似性特征, 对接收信号的包络变化、瞬时频率变化这两个重要的参数进行了估计.方法与信号的统计特性无关, 即使有两个或多个信号分量的概率密度函数是高斯分布的, 只要对应的脊能够区分开来, 即可分别提取并重构信号.此外, 对于含噪声的通信环境中, 信号能量集中在脊所在位置上的, 而噪声能量分布在整个时频平面上, 因此信号能量更为突出, 有利于脊的提取.然而这种方法不足的地方在于没有考虑信号相位的信息, 当信号的背景噪声较大时, 往往对相位的影响较大, 导致不能正确提取脊.因此在对相位要求较严的场合, 这种方法有局限性.
针对非合作环境下单通道成对载波多址(PCMA, paired carrier multiple access)信号的欠定盲源分离问题, 文献[31]中将实际应用中存在的频偏、定时偏差、初始相位等诸多不确定因素考虑进来, 建立了单通道下两路同频混合调制信号基带处理的一般性模型, 分析了混合信号间的状态空间差异, 利用该状态空间差异把盲源分离问题转化成了未知参数和信息符号的联合估计问题, 得到了很好的分离效果.但文献中的分离主要以两路源信号的混合为主, 对于高维状态的滤波问题, 需要大量的粒子数才能准确的估计后验分布, 计算量很大, 在满足实际应用的实时性方面有待进一步提高.
针对语音信号的单通道盲分离问题, 文献[32]中考虑噪声和声源回声同时存在的情况下, 建立自回归混响模型, 在时频域中通过隐性半马尔科夫链的方法进行语音信号检测, 并利用扩展型卡尔曼滤波方法估计出接收信号的混响时间参数和直达声源与回响声源能量的比值参数(DRR, direct-to-reverberant energy ratio), 根据得到的两个参数进行联合估计, 分离出有用的声源信号.该方法的估计延迟较小, 具有实时检测和在线估计的能力.
3.5 基于有限符号集特征的估计方法基于有限符号集特征的估计方法依据这样的一个事实, 即通信信号具有有限符号集特征, 可以用序列符号和参数进行准确描述, 因此可采用序列检测和联合参数估计的思想来实现单通道混合信号的盲分离.基于有限符号集特征的估计方法是近几年来提出的一类有效手段, 许多学者已经做了大量而有效的奠基性工作.目前, 对于基于有限符号集特征的估计方法的研究可以总结为以下几个方面.
3.5.1 基于粒子滤波的单通道盲源分离算法粒子滤波算法[33]又称为序列蒙特卡洛法(SMC, sequential Monte Carol), 基本思想是对未知变量的后验概率分布进行蒙特卡洛采样, 调整每个采样点的权重来逼近最终的概率分布函数.每个采样点称为一个粒子, 当粒子数足够多时, 就能够逼近任意复杂度的概率分布函数.粒子滤波算法提供了一种解决非线性、非高斯模型问题有效而便利的途径.另外, 由于粒子滤波是贝叶斯最优估计的近似实现方法, 因此基于粒子滤波的算法性能较好, 但由于基于粒子滤波的单通道盲源分离算法是基于最大似然准则, 因而该类算法的复杂度随着调制阶数的增加呈指数增长, 计算复杂度过高.
文献[34]中首次将粒子滤波算法应用到单通道盲源分离中, 标志着盲源分离研究领域的一大进步.但是在盲源分离算法实现的过程中, 随着信号调制阶数的增加和粒子数的增加, 整个算法的运算量和复杂度会大幅度增加, 并且无法解决粒子退化问题.
针对基于粒子滤波盲源分离算法运算复杂度高的问题, 文献[35]中将支持向量机(SVM, support vector machine)理论引入到粒子滤波算法中, 提出一种数字调制混合信号的单通道盲源分离算法.利用SVM理论, 从整个粒子集中选出对概率密度函数贡献较大的部分粒子, 在保证粒子多样性的前提下降低了粒子权值更新部分的运算量.与传统基于粒子滤波的单通道盲分离算法相比, 该算法在误码率相当的情况下, 有效缩短了运算时间.但由于SVM是借助二次规划来求解支持向量, 而求解二次规划将涉及m阶矩阵的计算(m为样本的个数), 当m数目很大时该矩阵的存储和计算将耗费大量的机器内存和运算时间.
路威, 张邦宁等[36]提出了一种基于遗传粒子滤波的单通道盲分离算法.通过建立一路通信体制已知的通信信号与恶意单音干扰混合后的信号状态空间模型, 在此基础上, 利用粒子滤波对通信码元和未知参数进行联合估计.针对传统粒子滤波中可能存在的粒子退化现象, 采用遗传进化机制进行粒子重采样, 通过选择、交叉、变异等遗传进化操作, 从而既保留了优质粒子又不损失粒子集合在序贯估计过程中的多样性.但由于贝叶斯估计的性能会随着待估参数数量的增加而下降, 因此, 该算法适用于需要较少参数描述的信号进行分离(如单音干扰, 线性调频(LFM, linear frequency modulation)低阶调制信号), 而不适用于估参数过多的信号的分离, 比如多音干扰信号、高阶调制信号.
此外, 为了减少基于粒子滤波的单通道盲源分离算法的运算时间、提高运算效率, 许多文献中[37-39]中也对该算法中粒子滤波的实现进行了分析与改进, 以加快粒子滤波算法的运算速度, 提升运算效率.
3.5.2 基于MCMC的单通道盲源分离算法马尔可夫链蒙特卡洛(MCMC, Markov chain Monte Carlo)的基本思想是利用不可约马尔可夫过程的可逆平稳分布的性质, 先构造一条Markov链, 使其平稳分布为所期望的分布, 当Markov链达到平稳分布时, 从中抽取样本作为数据样本.故马尔可夫蒙特卡洛方法的重点就是根据平稳分布来构造满足以上性质的马尔可夫转移核[40-41].常用的方法有吉布斯抽样(Gibbs sampler)[42]和米特罗波利斯算法(Metropolis algorithm)[43].
在无线通信领域, 将MCMC方法用于MIMO通信系统的信号估计中可以取得接近信道容量的优良性能[44].文献[45]针对粒子滤波方法中存在的问题, 给出了两种增强算法:正则化粒子滤波(RPF, regularized particle filtering)和加入了马尔可夫链蒙特卡洛的粒子滤波(PF.MCMC), 在参数估计精确度和计算复杂度上做了进一步改善, 降低误码率.
文献[46]中根据单通道接收两路MPSK混合信号在过采样下的基本模型, 提出了一种基于MCMC的单通道盲源分离算法, 该算法通过MCMC方法来计算多进制相移键控(MPSK, multiple phase shift keying)符号的后验概率, 近似实现了贝叶斯最优估计.通过在单通道MPSK信号盲源分离模型上进行Gibbs采样、后验概率计算, 实现了参数的最小二乘更新以及符号的最大后验概率估计.与基于粒子滤波的算法相比, 基于MCMC的算法能取得更好的误码率性能和更低的复杂度, 同时由于采用了过采样方式进行处理, 该算法对信号的波形信息利用更加充分, 能很好地抑制噪声.
类似地, 文献[47]中针对非合作接收的两路单通道同频混合信号, 提出了一种基于Gibbs采样和MCMC的单通道盲源分离算法, 降低了分离算法的运算复杂度.该算法利用统计的方法获得未知符号序列概率密度的随机样本, 运算复杂度不会随调制阶数的增加呈指数增长, 提高了算法的运行效率.但对于更高维的混合信号和在信噪比不够高的情况下, 该算法的分离效果将会受到影响.
3.5.3 基于PSP的单通道盲源分离算法逐幸存路径处理(PSP, per-survivor processing)算法[48]是一种近似的最大似然序列估计(MLSE, maximum likelihood sequence estimation)算法, 一般广泛用于单路信号情况下码元符号序列和信道的盲估计.其基本思想是将基于数据辅助的未知参数估计技术嵌入到维比特算法中, 来实现参数与序列的联合估计.
假设接收到的信号序列x由两路源信号混合而成, 盲源分离的目的是根据接收序列x估计出两路信号的符号序列{a1, k, a2, k, k=0, 1, …}, 可采用最大似然估计法进行估计.由于信道响应{g1, k, g2, k, k=0, 1, …}未知, 因此最大似然估计需要在参数和序列组成的联合空间进行:
| $\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} = \mathop {\arg {\rm{ }}\max }\limits_{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }},{\rm{ }}\mathit{\boldsymbol{G}}} {\rm{ }}p\left( {\mathit{\boldsymbol{x}}/\mathit{\boldsymbol{ \boldsymbol{\varPhi} }},{\rm{ }}\mathit{\boldsymbol{G}}} \right)$ | (7) |
其中:Φ表示由{φk=(a1, k, a2, k), k=0, 1, …}组成的符号序列, 参数G表示由{g1, k, g2, k, k=0, 1, …}组成的信道响应, x={xk, k=0, 1, …}.因此, 基于PSP的混合信号单通道盲源分离算法可以简要描述如下:
1) 初始化:设置时刻k=0, 设定初始状态s0, 将累计路径度量Γ(s0)初始化为0, 信道初始响应为g1, 0和g2, 0.
2) 输出符号对:若k≥δ, 根据最优留存路径输出(k-δ)时刻的符号对(a1, k-δ, a2, k-δ), 其中δ为判决延迟.
3) 扩展分支:设置k=k+1, 根据输入符号对(a1, k+L2+1, a2, k+L2+1)的M2(M为调制阶数)种不同取值从每一留存路径中扩展出M2条分支, 计算k时刻的分支度量λ:λ(sk-1→sk)=|e(sk-1→sk)|2, 其中:e(sk-1→sk)=yk-g1, kTa1, k(sk-1→sk)-g2, kTa2, k(sk-1→sk), ai, k(sk-1→sk)是状态转移sk-1→sk对应的第i路信号的符号向量.
4) 保留路径:对汇聚到每个状态的M2条分支路径, 计算累积路径度量
5) 参数更新:根据
| $\mathit{\Gamma }({\mathit{\boldsymbol{s}}_k}) = \mathop {\min }\limits_{{\phi _k} + {L_2}} (\mathit{\Gamma }(\mathit{\boldsymbol{s}}_{k - 1}^{{\phi _k} + {L_2}}) + \lambda ({\mathit{\boldsymbol{s}}_{k-1}} \to {\mathit{\boldsymbol{s}}_k}))$ |
对信道响应进行更新, 然后回到步骤2).
文献[49]中提出的基于最小均方误差逐幸存路径处理(LMS-PSP, least mean square per-survivor processing)的单通道盲源分离算法将信道参数等效为信道冲激响应(CIR, channel impulse response), 只需在序列估计的同时进行滤波器系数更新即可, 虽然较粒子滤波算法显著地降低了复杂度, 但还是偏高, 且在时变信道下该算法的分离性能较差.为进一步提升PSP算法在解决单通盲分离问题时的运行效率, 文献[50]提出一种基于基扩展模型逐幸存路径处理(BEM-PSP, basis expansion model persurvivor processing)的单通道盲源分离算法.算法在复杂度减半的情况下性能明显优于LMS-PSP算法, 且在同等过采样倍数下比LMS-PSP算法能获得更高的性能提升.
针对高斯最小频移键控(GMSK, Gaussian filtered minimum shift keying)信号的单通道盲源分离问题, 廖灿辉等[51]根据GMSK信号的特点, 将PSP思想引入到了GMSK混合信号的单通道盲源分离中.考虑到实际中的GMSK信号一般是突发信号, 而突发混合信号具有时长短、参数估计误差大的特点, 基于此特点, 文献中进一步提出了一种抗频偏的改进算法, 不需要进行初始相位估计, 并且能容忍较大的初始频偏估计误差.
除了上面提到的几类主流的单通道盲源分离方法外, 还有其它一些近年来提出的有效分离方法, 如基于非负矩阵分解的方法、基于深度神经网络的方法等[52-56].由于篇幅有限, 便不再一一展开介绍.
4 单通道盲信号分离的应用单通道盲源分离技术以其系统简单、成本低廉的明显优势, 在信号处理众多领域内具有良好的应用前景, 下面将对单通道盲源分离的一些主要应用领域进行简单的介绍.
1) 信号去噪
在接收条件或信道非理想的情况下, 接收到的信号质量往往不佳, 因此, 对接收信号的去噪成为信号处理领域中比较重要的研究课题.文献[57]中利非负矩阵分解的思想将混有噪声的语音信号进行重构, 从而达到增强信号和消除噪声的效果.
2) 通信对抗
在通信对抗领域中, 需要识别敌方电台设备, 这样首先需要架设天线来截获敌方电台发射的信号.由于现实环境比较复杂且不宜架设过多的天线, 截获的信号往往掺杂着其他电台发射的信号和噪声, 当接收环境比较恶劣时, 使用一根天线接收, 具有更高的实用性, 因此单通道盲源分离技术被广泛的应用于通信对抗领域.文献[58]在已知干扰信号循环谱的条件下, 用单路接收天线截获敌方的雷达探测信号.
3) 生物医学信号处理
在生物医学领域中, 源信号经常是比较微弱的, 容易和其他的生理信号叠加在一起.当只有一个记录通道时, 能够从混合信号中分离出感兴趣的信号具有重要的意义.文献[59]通过接收单路的人体脑电波(EEG, Electroencephalogram), 运用相应的算法, 检测出人体不同的睡眠状态, 从而能够协助医学诊断.
4) 状态监测与故障诊断
在机械状态检测与故障诊断中, 通过提取的机械振动信号来了解和掌握部件在运行过程中的状态, 确定该部件是否正常运转.一个接收传感器可以用来获取多个部件的振动信号, 这样就需要单通道盲分离技术从单路混合信号中提取出各个部件的震动信号, 然后分别分析各部件的运行状态.文献[60]中利用小波变换和Fourier变换, 将单路观测信号进行小波分解, 分离出监测特征信号.
5) 语音信号处理
语音信号处理是单通道盲分离的传统应用领域, 如经典的“鸡尾酒会”问题.对于只有单路麦克风, 存在多路声源的情况, 就需要利用单通道盲分离算法对各路声源信号进行分离和识别.文献[61]中运用经验模式分解方法和Hilbert-Huang变换方法对单路接收混合信号进行处理, 成功分离出两路不同的语音信号.
5 单通道盲源分离研究存在的挑战以及研究展望单通道盲源分离在近年来已经取得了令人欣慰的发展, 针对不同的应用场合提出了若干新理论和新方法, 并取得了初步的成功.但是当前的理论研究和发展还尚未成熟, 需要有进一步的突破, 目前还存在的问题如下:
1) 大多数文献中, 源信号数目均为假设条件, 一般假设为两个源信号的混合, 对于源信号数目准确估计问题并未深入讨论, 而且在信号分量数目较多的情况下算法的普适性有待研究;
2) 现有的单通道盲分离算法在计算复杂度方面有待进一步改善.虽然很多文献中都在降低算法复杂度方面做了大量的工作, 但总体上算法的复杂度还是偏高, 对于包含两个信号分量以上的混合信号, 算法更为复杂, 缺乏实用价值;
3) 大多数算法需要提供训练样本进行信道估计, 有些还对训练样本有特殊要求, 并非真正意义上的全盲;
4) 对信噪比要求较高, 无法保证在低信噪比条件下算法的性能.现在很多提出的算法都是在假设无噪声的情况下或把噪声看作一个独立源信号的前提下进行的, 这与实际信号传输环境不符.
鉴于以上问题, 文中给出了几个值得进一步研究的方向:
1) 对混合信号中信号分量数目估计的问题值得进一步研究, 同时寻找在信号分量数目较多的情况下进行分离时行之有效的新方法.
2) 进一步研究复杂度低, 计算量小且收敛速度快的新算法.
3) 在解决单通道盲源分离问题时, 加入对噪声和实时环境的考虑.已有的盲源分离方法在什么情况下可以应用到一般的噪声混迭模型, 也是一个有待研究的问题.
4) 进行单通道复值信号的盲分离研究.复值信号的盲分离是单通道信号处理过程中经常遇到的问题, 而现有的算法一般仅针对实信号的处理.
6 结束语单通道盲源分离是信号处理领域的一个重要研究方向, 在数字通信、图像处理、生物医学、语音信号处理等领域有着广泛的应用前景.综述在阐述了单通道盲分离的基本数学模型和分离思想的基础上, 分类讨论了近几年来主流的几类单通道盲源分离算法, 包括它们的基本原理、特点以及优缺点, 最后指出了单通道盲源分离的应用领域以及当前研究所面临的问题与挑战, 并结合当前的研究状况对单通道盲源分离未来可能的发展方向进行了分析.单通道盲源分离技术发展较晚, 目前许多提出的理论和技术还尚未成熟, 需要大量的工作去研究和挖掘更多的新理论、新方法和新应用, 进一步完善盲源分离领域的发展.
| [1] |
权友波, 王甲峰, 岳旸, 等. 盲源分离技术现状及发展趋势[J]. 通信技术, 2011, 44(4): 13–15.
Quan Youbo, Wang Jiafeng, Yue Yang, et al. Present situation and development trend of blind source separation[J]. Communications Technology, 2011, 44(4): 13–15. |
| [2] | Hopgood J R, Rayner P J W. Single channel nonstationary stochastic signal separation using linear time-varying filters[J]. Signal Processing IEEE Transactions on, 2003, 51(7): 1739–1752. doi: 10.1109/TSP.2003.812837 |
| [3] | Cohen L. What is a multicomponent signal?[C]//IEEE International Conference on Acoustics, Speech, and Signal Processing. San Francisco:IEEE, 1992:113-116. |
| [4] | Hopgood J R, Rayner P J W. Single channel signal separation using linear time varying filters, IEEE International Conference on Acoustics, Speech and Signal Processing, 1999, 3:1449-1452. |
| [5] | Hansen L K, Petersen K B. Monaural ICA of white noise mixtures is hard[C]//Independent Component Analysis, 2003. Nara:Independent Component Analysis, 2003:815-820. |
| [6] |
蔡权伟, 魏平, 肖先赐. 信道重叠信号分离方法的发展与展望[J]. 电子学报, 2005, 33(33): 2446–2454.
Cai Quanwei, Wei Ping, Xiao Xianci. A review of single channel separation algorithms of overlapped multi-components[J]. Acta Electronica Sinica, 2005, 33(33): 2446–2454. |
| [7] |
徐明彪, 朱维彰. 关于信号盲分离的分离效果评判指标的分析[J]. 杭州电子科技大学学报, 2002, 22(3): 63–66.
Xu Mingbiao, Zhu Weizhang. Analyses of the index used for evaluating the effect of BSS[J]. Journal of Hangzhou Institute of Electronic Engineering, 2002, 22(3): 63–66. |
| [8] |
邓智恒, 罗伟栋. 实际语音盲分离客观评价指标研究[J]. 电声技术, 2007, 31(9): 61–65.
Deng Zhiheng, Luo Weidong. Performance evaluation for speech signals blind separation in real-environment[J]. Audio Engineering, 2007, 31(9): 61–65. |
| [9] | Jutten C, Herault J. Blind separation of sources, part Ⅰ:An adaptive algorithm based on neuromimetic architecture[J]. Signal Processing, 1991, 24(1): 1–10. doi: 10.1016/0165-1684(91)90079-X |
| [10] | He Pengju, She Tingting, Li Wenhui, et al. Single channel blind source separation on the instantaneous mixed signal of multiple dynamic sources[J]. Mechanical Systems and Signal Processing, 2017(12): 64–68. |
| [11] |
何继爱, 李玉芬, 张玺君. 基于EMD的单通道通信信号盲分离算法研究[J]. 甘肃科学学报, 2015, 27(4): 14–19.
He Jiai, Li Yufen, Zhang Xijun. Research on blind source separation algorithm of single channel communication signal based on EMD[J]. Journal of Gansu Sciences, 2015, 27(4): 14–19. |
| [12] | Mourad N, Niazy R K. Automatic correction of eye blink artifact in single channel EEG recording using EMD and OMP[C]//EUSIPCO 2014. Marrakech:IEEE, 2014:1-5. |
| [13] | Deng Xianrong, Pang Lihui, Jiang Kaili, et al. Single-channel blind signal separation method for time-frequency overlapped signal based on CEEMD-FastICA[C]//ICSP 2017. Chengdu:IEEE, 2017:1440-1445. |
| [14] |
齐扬阳, 于淼. 基于EMD的单通道盲源分离跳频通信抗干扰方法[J]. 计算机科学, 2016, 43(1): 149–153.
Qi Yangyang, Yu Miao. Anti-jamming method for frequency hopping communication based on single channel BSS and EMD[J]. Computer Science, 2016, 43(1): 149–153. doi: 10.11896/j.issn.1002-137X.2016.01.034 |
| [15] | Qi Yangyang, Yu Miao, Chen Jianzhong. An anti-Jamming method for frequency-hopping communication based on single channel BSS of wavelet packet[J]. Communications Technology, 2014(12): 1360–1365. |
| [16] | Gómez A, Quintero L, López N, et al. An approach to emotion, recognition in single channel EEG signals using stationary wavelet transform[J]. 2017. |
| [17] |
王翔, 黄知涛, 周一宇. 基于循环频域滤波及Schmidt正交对消的单通道信号分离算法[J]. 国防科技大学学报, 2012, 34(4): 120–125.
Wang Xiang, Huang Zhitao, Zhou Yiyu. Single channel signal separation algorithm based on cyclostationary filtering and Schmidt orthogonal cancellation[J]. Journal of National University of Defense Technology, 2012, 34(4): 120–125. |
| [18] | Dong Shaojiang, Tang Baoping, Zhang Yan. A repeated single channel mechanical signal blind separation method based on morphological filtering and singular value decomposition[J]. Measurement, 2012, 45(8): 2052–2063. doi: 10.1016/j.measurement.2012.05.003 |
| [19] | Jeong I Y, Kim B, Park H M. Single channel speech dereverberation based on non-negative blind deconvolution and prior imposition on speech and filter[M]//Neural Information Processing, 2013:469-476. |
| [20] |
何继爱, 刘琳芝, 李英堂. LCL-FRESH滤波器实现单通道盲源分离[J]. 信号处理, 2014, 30(2): 236–242.
He Jiai, Liu Linzhi, Li Yingtang. Single channel blind source separation achieved by the LCL-FRESH filter[J]. Journal of Signal Processing, 2014, 30(2): 236–242. |
| [21] |
杨海兰, 刘以安. 单通道通信信号盲分离算法[J]. 计算机仿真, 2015, 32(9): 205–208.
Yang Hailan, Liu Yian. Blind separation algorithm of single channel communication signals[J]. Computer Simulation, 2015, 32(9): 205–208. |
| [22] |
朱行涛, 刘郁林, 何为, 等. 基于变换域滤波的直扩通信单通道混合信号分离抗干扰方法[J]. 系统工程与电子技术, 2016, 38(10): 2405–2412.
Zhu Xingtao, Liu Yulin, He Wei, et al. Anti-jamming algorithm for direct sequence spread spectrum communication based on source separation of single channel mixed signal by using transform-domain filter[J]. Systems Engineering and Electronics, 2016, 38(10): 2405–2412. doi: 10.3969/j.issn.1001-506X.2016.10.26 |
| [23] | Yin Ming, Gao Junbin, Tien D, et al. Blind image deblurring via coupled sparse representation[J]. Journal of Visual Communication and Image Representation, 2014, 25(5): 814–821. doi: 10.1016/j.jvcir.2014.02.003 |
| [24] | Wohlberg B. Efficient algorithms for convolutional sparse representations[J]. IEEE Transactions on Image Processing, 2015, 25(1): 301–315. |
| [25] | Mairal J, Bach F, Ponce J, et al. Online learning for matrix factorization and sparse coding[J]. Journal of Machine Learning Research, 2010, 11(1): 19–60. |
| [26] | Qiao Jianyong. Julia sets and complex singularities of free energies[J]. Memoirs of American Mathematical Society, 2015(234): 1–89. |
| [27] | Févotte C, Godsill S J, Wolfe P J. Bayesian approach for blind separation of underdetermined mixtures of sparse sources[J]. Lecture Notes in Computer Science, 2004, 3195: 398–405. doi: 10.1007/b100528 |
| [28] | Smith E C, Lewicki M S. Efficient auditory coding[J]. Nature, 2006, 439(7079): 978–982. doi: 10.1038/nature04485 |
| [29] |
朱会杰, 王新晴, 芮挺, 等. 基于移不变稀疏编码的单通道机械信号盲源分离[J]. 振动工程学报, 2015, 28(4): 625–632.
Zhu Huijie, Wang Xinqing, Rui Ting, et al. Shift invariant sparse coding for blind source separation of single channel mechanical signal[J]. Journal of Vibration Engineering, 2015, 28(4): 625–632. |
| [30] |
张晓冬, 王桥, 吴乐南. 利用脊的特征进行信号盲分离[J]. 电子学报, 2004, 32(7): 1156–1159.
Zhang Xiaodong, Wang Qiao, Wu Lenan. Blind source separation based on ridge characterization extraction[J]. Acta Electronica Sinica, 2004, 32(7): 1156–1159. |
| [31] | 刘凯. 粒子滤波在单通道信号分离中的应用研究[D]. 中国科学技术大学, 2007. |
| [32] | Doire C S J, Brookes M, Naylor P A, et al. Single channel blind estimation of reverberation parameters[C]//IEEE International Conference on Acoustics, Speech and Signal Processing. IEEE, 2015:31-35. |
| [33] | Djuric P M, Kotecha J H, Zhang J, et al. Particle filtering[J]. IEEE signal processing magazine, 2003, 20(5): 19–38. doi: 10.1109/MSP.2003.1236770 |
| [34] | Liu Kai, Li Hui, Dai Xuchu, et al. Single channel blind signal separation of cofrequency MPSK signals[C]. Proceedings of International Conference on Communication, Internet and Information Technology (CⅡT 2006), St. Thomas, USVI, USA, Nov. 2006:42-46. |
| [35] |
栾海妍, 江桦, 刘小宝. 利用粒子滤波与支持向量机的数字混合信号单通道盲分离[J]. 应用科学学报, 2011, 29(2): 195–202.
Luan Haiyan, Jiang Hua, Liu Xiaobao. Single channel blind source separation of digital mixtrures using particle filtering and support vector machine[J]. Journal of Applied Sciences, 2011, 29(2): 195–202. |
| [36] |
路威, 张邦宁, 张杭. 利用遗传粒子滤波的单通道扰信盲分离算法[J]. 数据采集与处理, 2014, 29(5): 783–789.
Lu Wei, Zhang Bangning, Zhang Hang. Single channel bind separation of communication signal and interference using genetic particle filtering[J]. Journal of Data Acquisition and Processing, 2014, 29(5): 783–789. |
| [37] | Feng Hao, Gao Yong. High-speed parallel particle filter for PCMA signal blind separation[J]. Radioelectronics and Communications Systems, 2016, 59(10): 455–462. doi: 10.3103/S0735272716100058 |
| [38] | Monajemi S, Jarchi D, Ong S H, et al. Cooperative Particle Filtering for Tracking ERP Subcomponents from Multichannel EEG[J]. Entropy, 2017, 19(5): 199. doi: 10.3390/e19050199 |
| [39] | Bordin C J, Bruno M G S. Distributed particle filtering for blind equalization in receiver networks using marginal non-parametric approximations[C]//ICASSP 2014. Florence:IEEE, 2014:7984-7987. |
| [40] | Haji-Sheikh A, Howell J R. Monte Carlo methods[M]. Second Edition, 2009: 249-295. |
| [41] | Qiao Jianyong. On the preimages of parabolic points[J]. Nonlinearity, 2000(13): 813–818. |
| [42] | Neal R M. Markov chain sampling methods for Dirichlet process mixture models[J]. Journal of Computational and Graphical Statistics, 2000, 9(2): 249–265. |
| [43] | Wang Hongrui, Wang Cheng, Wang Ying, et al. Bayesian forecasting and uncertainty quantifying of stream flows using Metropolis-Hastings Markov chain Monte Carlo algorithm[J]. Journal of Hydrology, 2017(7): 549. |
| [44] | Chen Rongrong, Peng Ronghui, Ashikhmin A, et al. Approaching MIMO capacity using bitwise Markov chain Monte Carlo detection[J]. IEEE Transactions on Communications, 2010, 58(2): 423–428. doi: 10.1109/TCOMM.2010.02.080533 |
| [45] | 李响. 基于粒子滤波的单通道盲分离算法研究[D]. 郑州大学, 2012. http://d.wanfangdata.com.cn/Thesis/Y2102797 |
| [46] |
汤俊杰, 李辉, 戴旭初. 实现单通道MPSK信号盲分离的MCMC新算法[J]. 信号处理, 2014(11): 1321–1328.
Tang Junjie, Li Hui, Dai Xuchu. Blind separation algorithm of single channel MPSK signals based on MCMC[J]. Journal of Signal Processing, 2014(11): 1321–1328. doi: 10.3969/j.issn.1003-0530.2014.11.014 |
| [47] | Yang Yong, Zhang Dongling, Peng Hua. Single channel blind separation of co-frequency modulated signals based on Gibbs sampler[J]. Journal on Communications, 2015, 36(4): 156–162. |
| [48] | 万坚. 通信混合信号盲分离理论与技术[M]. 北京: 国防工业出版社, 2012: 253-277. |
| [49] | Tu Shilong, Zheng Hui, Gu Na. Single channel blind separation of two QPSK signals using per-survivor processing[C]//APCCAS 2009. Macao:IEEE, 2009:473-476. |
| [50] |
熊涛, 江桦, 崔鹏辉, 等. 应用基扩展模型的混合信号单通道盲分离算法[J]. 西安交通大学学报, 2015, 49(6): 60–66.
Xiong Tao, Jiang Hua, Cui Penghui, et al. A single channel blind separation algorithm for mixed signals applying the base expansion model[J]. Journal of Xi'an Jiaotong University, 2015, 49(6): 60–66. doi: 10.7652/xjtuxb201506010 |
| [51] |
廖灿辉, 涂世龙, 万坚. 抗频偏的突发GMSK混合信号单通道盲分离算法[J]. 通信学报, 2013, 5(5): 88–95.
Liao Canhui, Tu Shilong, Wan Jian. Anti-frequency-offset algorithm on single channel blind separation of burst GMSK mixed signals[J]. Journal on Communications, 2013, 5(5): 88–95. |
| [52] | Yoshii K, Itoyama K, Goto M. Student's T nonnegative matrix factorization and positive semidefinite tensor factorization for single-channel audio source separation[C]//ICASSP 2016. Shanghai:IEEE, 2016:51-55. |
| [53] | Pham T, Lee Y, Lin Yanbo, et al. Single channel source separation using sparse NMF and graph regularization[C]//ASE Bigdata and Socialinformatics 2015. Kaohsiung:ACM, 2015:55. |
| [54] | Grais E M, Roma G, Simpson A J R, et al. Discriminative enhancement for single channel audio source separation using deep neural networks[J]. 2017. |
| [55] | Han Wei, Zhang Xiongwei, Min Gang, et al. A novel single channel speech enhancement based on joint deep neural network and wiener filter[C]//PIC 2016. Nanjing:IEEE, 2016:163-167. |
| [56] | Qiao Jianyong. Two problems in the value distribution theory[J]. Acta Math Sinica (N), 1995(11): 365–371. |
| [57] | Lee S, Han D K, Ko H. Single channel speech enhancement method using reconstructive NMF with spectrotemporal speech presence probabilities[J]. Applied Acoustics, 2016. |
| [58] | Yeste-Ojeda O A, Grajal J. Cyclostationarity-Based Signal in Interceptors Based on a Single Sensor[C]//Radar Conference. Rome:IEEE, 2008:1-6. |
| [59] | Hassan A R, Subasi A. A decision support system for automated identification of sleep stages from single channel EEG signals[J]. Knowledge-Based Systems, 2017. |
| [60] | Chen Guohua, Qie Longfei, Zhang Aijun, et al. Improved CICA algorithm used for single channel compound fault diagnosis of rolling bearings[J]. Chinese Journal of Mechanical Engineering, 2016, 29(1): 204–211. doi: 10.3901/CJME.2015.1026.127 |
| [61] | Krishna P K M, Ramaswamy K. Single Channel speech separation based on empirical mode decomposition and Hilbert Transform[J]. IET Signal Processing, 2017. |


