为了提高低密度扩展(LDS)系统性能对LDS多用户检测算法进行研究,提出了一种LDS非正交多址系统中多用户检测和信道编码译码联合迭代的方案.将各用户低密度奇偶校验码(LDPC)译码后的软信息回传给多用户检测器,提高了多用户符号检测的可靠性,而多用户检测性能的提高又进一步提高了LDPC码译码的性能.在相同条件下与多用户检测和LDPC码译码单独进行的方案进行了仿真对比,结果表明,联合迭代算法明显改善了误比特率,系统负载越大,联合迭代带来的性能改善也越大.同时,联合迭代还缩小了不同用户误码性能的差异且即使在系统负载达到200%时,误码性能也与单用户的性能相差不大.联合迭代算法在不增加接收机计算复杂度的情况下,显著提升了LDS系统的性能.
The LDS multiuser detection algorithm was researched to improve the performance of LDS system. A joint scheme of multiuser detection and channel decoding in LDS non-orthogonal multiple access systems was introduced. The reliability of multiuser detection was improved by transmitting users' soft information after LDPC decoder back to multiuser detector. The performance of channel decoding was further improved by the enhancement of multiuser detection. Simulations, comparing with multiuser detecting and LDPC code decoding separately under the same conditions, indicate that the joint iterative algorithm can significantly improve the performance of BER. It is shown that the larger the system load is, the greater the performance improvements. At the same time, the difference in error performance between different users also reduces by the joint scheme. With the joint iterative algorithm, the performance of BER is almost same as that of single user even when the system load reaches 200%. The performance of the LDS system is significantly improved without increasing computational complexity of receiver by the joint scheme.
近年非正交多址接入技术(NOMA, non-orthogonal multiple access)[1-2]受到了广泛关注.功率域NOMA是基于功率域复用的多址技术[3-4].低密度扩展[5-7] (LDS, low-density spreading),是编码域NOMA技术的一种,对其多用户检测算法进行优化是研究的热门问题[8-9].除LDS,编码域NOMA技术还有稀疏码多址接入[10],多用户共享接入,图样分割多址接入[11-12]等.两类NOMA主要采用的多用户检测算法分别为串行干扰消除算法(SIC, serial interference cancellation)[13]和消息传递(MP, message passing)算法.
给出一种在LDS多用户检测和LDPC码译码间进行软信息联合迭代传递的算法,通过在多用户检测器和LDPC码译码器间软信息的迭代,在不增加接收机复杂度的情况下降低信息接收错误率.最后给出仿真结果和分析.
1 LDS-NOMA系统结构在码分多址(CDMA, code division multiple access)系统中,K个用户的信息经过扩频调制到N个码片上.假设信道为高斯白噪声信道,所有用户信号叠加后通过信道传输后接收端的接收信号为
| $ \mathit{\boldsymbol{y}} = \sum\limits_{k = 1}^K {{\mathit{\boldsymbol{s}}_k}{\mathit{\boldsymbol{x}}_k} + \mathit{\boldsymbol{z}}} = \mathit{\boldsymbol{Sx}} + \mathit{\boldsymbol{z}} $ | (1) |
其中:y=[y1 y2 … yN]T为接收信号矢量;sk=[s1, k s2, k … sN, k]T为用户k的扩展序列;xk为用户k的发送符号;z为服从复高斯分布的白噪声矢量,z~CN[0, σ2I];S和x分别为K个用户的扩展矩阵和发送符号矢量.
传统的CDMA系统中,扩展矩阵的元素通常为非零值,序列与序列之间为正交或准正交关系.接收端接收到的码片n上的信号为
| $ {y_n} = \sum\limits_{k = 1}^K {{s_{n,k}}{x_k} + {z_n}\left( {n = 1,2, \cdots ,N} \right)} $ | (2) |
码片n携带了所有K个用户的信息.对每个用户而言,在每个码片上都受到了来自其他K-1个用户的多址干扰(MAI, multiple access interference).当各用户的扩展序列间正交或准正交时,采用简单的方法就可消除或减小MAI.当系统用户数K大于码片数N即系统过载的情况下,扩展序列之间不再正交,接收端为消除或降低MAI的影响,多用户检测的复杂度会大大增加.
在LDS系统中,用户的扩展序列采用低密度的签名序列,用户的信息不再扩展到全部N个码片上,而是只在一小部分码片上扩展信息,而一个码片上也只携带一小部分用户的信息.用dv和dc分别表示每个用户扩展信息的最大码片数和每个码片承载的最大用户数,且dv≪N,dc≪K.所有用户的扩展序列合成的签名矩阵中非零值较少,矩阵为稀疏矩阵.采用稀疏签名矩阵的好处是可降低多用户检测的复杂度.
N个码片、K个用户的系统扩展矩阵表示为
| $ \mathit{\boldsymbol{S}} = \left[ {\begin{array}{*{20}{c}} {{s_{1,1}}}&{{s_{1,2}}}&{}&{{s_{1,K}}}\\ {{s_{2,1}}}&{{s_{2,2}}}& \cdots &{{s_{2,K}}}\\ {}& \vdots &{}&{}\\ {{s_{N,1}}}&{{s_{N,2}}}&{}&{{s_{N,K}}} \end{array}} \right] $ | (3) |
为了更直观地描述LDS系统结构,引入标志矩阵F,其第n行第k列的元素为fn, k,S矩阵与F矩阵的关系表示为
| $ {f_{n,k}} = \left\{ \begin{array}{l} 0,\;\;\;{s_{n,k}} = 0\\ 1,\;\;\;{s_{n,k}} \ne 0 \end{array} \right.\left( \begin{array}{l} k = 1,2, \cdots ,K\\ n = 1,2, \cdots ,N \end{array} \right) $ | (4) |
F矩阵的第n行中1的位置集合代表第n码片上承载的用户集合,记为ξn,第k列中1的位置集合代表用户k扩展的码片集合,记为ζk.
LDS系统中接收端接收到的码片n上的信号为
| $ {y_n} = \sum\limits_{k \in {\xi _n}} {{s_{n,k}}{x_k} + {z_n}} = {\left( {{\mathit{\boldsymbol{s}}^{\left[ n \right]}}} \right)^{\rm{T}}}{\mathit{\boldsymbol{x}}^{\left[ n \right]}} + {z_n} $ | (5) |
其中:x[n]表示在码片n上传输数据的用户的符号组成的矢量,s[n]为S矩阵的第n中不为0的元素组成的矢量,zn表示噪声.
2 LDS多用户检测算法最优的多用户检测算法是最大后验概率(MAP, maximum a posteriori)检测,但是计算复杂度很高.由于LDS结构的低密度特性,可以使用低复杂度的次优码片级软信息迭代多用户检测算法,通过变量节点与函数节点之间消息的迭代更新来逼近最优的MAP检测.
采用MAP检测时,发送符号矢量x的估计为
| $ \mathit{\boldsymbol{\hat x}} = \arg \mathop {\max }\limits_x P\left( {\mathit{\boldsymbol{x}}\left| \mathit{\boldsymbol{y}} \right.} \right) $ | (6) |
在先验等概且噪声独立条件下先验概率为
| $ P\left( {\mathit{\boldsymbol{y}}\left| \mathit{\boldsymbol{x}} \right.} \right) = \prod\limits_{n = 1}^N {P\left( {{y_n}\left| \mathit{\boldsymbol{x}} \right.} \right)} $ | (7) |
在LDS系统中,每个码片只传输最多dc个用户的信息,因此
| $ P\left( {{y_n}\left| \mathit{\boldsymbol{x}} \right.} \right) = P\left( {{y_n}\left| {{\mathit{\boldsymbol{x}}^{\left[ n \right]}}} \right.} \right) $ | (8) |
在高斯白噪声信道下,第n个码片的条件概率为
| $ \begin{array}{*{20}{c}} {P\left( {{y_n}\left| {{\mathit{\boldsymbol{x}}^{\left[ n \right]}}} \right.} \right) = }\\ {\frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} \sigma }}\exp \left( { - \frac{1}{{2{\sigma ^2}}}{{\left| {{y_n} - {{\left( {{\mathit{\boldsymbol{s}}^{\left[ n \right]}}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{x}}^{\left[ n \right]}}} \right|}^2}} \right)} \end{array} $ | (9) |
其中,σ2表示噪声方差.
由于LDS系统中扩展矩阵的稀疏性,可以通过消息传递,采用迭代的方法,在较低的复杂度下近似MAP检测.将用户发送符号xk(k=1, 2, …, K)视为变量节点Vk,接收端信号yn(n=1, 2, …, N)视为函数节点Fn,消息在相连的变量节点和函数节点间不断迭代更新,传递的消息为代表该符号可靠度的软信息,文中为对数似然比.
记第i次迭代时变量节点Vk发给函数节点Fn的消息为LVk→Fn(i),函数节点Fn传给变量节点Vk的消息为LFn→Vk(i).假设采用二进制相移键控(BPSK, binary phase shift keying)调制方式,用户的发送符号xk∈{+1, -1}.变量节点和函数节点间传递的消息为符号的对数似然比值. Vk传给Fn消息为
| $ L_{{V_k} \to {F_n}}^{\left( i \right)} = \log \frac{{{P_{{\rm{ext}},n}}\left( {{x_k} = + 1} \right)}}{{{P_{{\rm{ext}},n}}\left( {{x_k} = - 1} \right)}} = \sum\limits_{m \in {\zeta _k}\backslash n} {L_{{F_m} \to {V_k}}^{\left( {i - 1} \right)}} $ | (10) |
其中,m∈ζk\n表示ζk中除开n的所有码片.特别地,第一次迭代时变量节点没有先验信息,因此LVk→Fn(0)=0, ∀n, ∀k.函数节点Fn传给变量节点Vk的消息为
| $ \begin{array}{*{20}{c}} {L_{{F_n} \to {V_k}}^{\left( i \right)} = \log \frac{{{P_{{\rm{ext}},n}}\left( {{y_n}\left| {{\mathit{\boldsymbol{x}}^{\left[ n \right]}}} \right.,{x_k} = + 1} \right)P\left( {{\mathit{\boldsymbol{x}}^{\left[ n \right]}}\backslash {x_k}} \right)}}{{{P_{{\rm{ext}},n}}\left( {{y_n}\left| {{\mathit{\boldsymbol{x}}^{\left[ n \right]}}} \right.,{x_k} = - 1} \right)P\left( {{\mathit{\boldsymbol{x}}^{\left[ n \right]}}\backslash {x_k}} \right)}} = }\\ {\log \frac{{\sum\limits_{\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{x}}^{\left[ n \right]}}}\\ {{x_k} = + 1} \end{array}} {\exp \left( {\sum\limits_{l \in {\zeta _n}\backslash k} {\frac{{{x_l}}}{2}L_{{V_k} \to {F_n}}^{\left( {i - 1} \right)}} } \right)P\left( {{\mathit{\boldsymbol{x}}^{\left[ n \right]}}\backslash {x_k}} \right)} }}{{\sum\limits_{\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{x}}^{\left[ n \right]}}}\\ {{x_k} = - 1} \end{array}} {\exp \left( {\sum\limits_{l \in {\zeta _n}\backslash k} {\frac{{{x_l}}}{2}L_{{V_k} \to {F_n}}^{\left( {i - 1} \right)}} } \right)P\left( {{\mathit{\boldsymbol{x}}^{\left[ n \right]}}\backslash {x_k}} \right)} }}} \end{array} $ | (11) |
该信息为码片n和ζk\n用户得出的xk的对数似然比信息.当迭代次数达到预设值I时多用户检测器输出K个用户符号的对数似然比软信息
| $ L_k^{{\rm{LDS}}} = \sum\limits_{n \in {\zeta _k}} {L_{{F_n} \to {V_k}}^{\left( I \right)}} $ | (12) |
接收机可以根据该软信息进行判决,也可以将其输入到信道编码的译码器进行信道编码的译码.
3 联合检测译码迭代算法LDS的消息传递(MP, message passing)算法中,通过不同用户间符号的关联性提高检测性能,而LDPC码的译码则通过(一个用户的)码字内码元间的关联性进行纠错.将LDPC码译码后得到的软信息再回传给多用户检测器,可帮助提高多用户符号检测的可靠性,而多用户检测可靠性的提高,进一步又提高了LDPC码译码的性能.
设LDPC码的码字长度为Q,每一次联合检测译码迭代(外迭代)中多用户检测MP算法的内迭代次数为I,LDPC码译码置信度传播(BP, belief pro-pagation)算法内迭代次数为J,联合检测译码外迭代次数为M,则MP算法的总迭代次数为I(M+1),BP算法的总迭代次数为J(M+1).
1) 多用户检测器对长度为N的信道输出扩展符号序列进行MP多用户检测,迭代I次后停止,输出K个用户符号的似然比软信息,将其记为一个矢量L1LDS=[L1, 1LDS L2, 1LDS … LK, 1LDS]T,其中的元素Lk, 1LDS(k=1, 2, …, K)为用户k的符号软信息.检测算法运行Q次,完成Q个扩展符号序列的多用户检测,得到Q个软信息矢量L1LDS, L2LDS, …, LQLDS,将其构成一个K×Q维的矩阵LLDS=[L1LDS L2LDS … LQLDS],也即
| $ {\mathit{\boldsymbol{L}}^{{\rm{LDS}}}} = \left[ {\begin{array}{*{20}{c}} {L_{1,1}^{{\rm{LDS}}}}&{L_{1,2}^{{\rm{LDS}}}}&{}&{L_{1,Q}^{{\rm{LDS}}}}\\ {L_{2,1}^{{\rm{LDS}}}}&{L_{2,2}^{{\rm{LDS}}}}& \cdots &{L_{2,Q}^{{\rm{LDS}}}}\\ {}& \vdots &{}&{}\\ {L_{K,1}^{{\rm{LDS}}}}&{L_{K,2}^{{\rm{LDS}}}}&{}&{L_{K,Q}^{{\rm{LDS}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{L}}_1^{{\rm{LDS}} \to {\rm{LDPC}}}}\\ {\mathit{\boldsymbol{L}}_2^{{\rm{LDS}} \to {\rm{LDPC}}}}\\ \vdots \\ {\mathit{\boldsymbol{L}}_K^{{\rm{LDS}} \to {\rm{LDPC}}}} \end{array}} \right] $ |
2) 将多用户检测后得到的K个用户符号的似然比软信息矢量LkLDS→LDPC(k=1, 2, …, K)分别传递给K个用户的LDPC译码器.
3) 每个用户的LDPC译码器将从多用户检测器传来的似然比软信息LkLDS→LDPC作为信道提供的信息,进行译码,J次迭代后输出Q维软信息矢量.记LkLDPC=[Lk, 1LDPC Lk, 2LDPC … Lk, QLDPC]为用户k的LDPC码译码器输出的软信息,K个用户LDPC码译码器输出的软信息矢量构成矩阵
| $ {\mathit{\boldsymbol{L}}^{{\rm{LDPC}}}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{L}}_1^{{\rm{LDPC}}}}\\ {\mathit{\boldsymbol{L}}_2^{{\rm{LDPC}}}}\\ \vdots \\ {\mathit{\boldsymbol{L}}_K^{{\rm{LDPC}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {L_{1,1}^{{\rm{LDPC}}}}&{L_{1,2}^{{\rm{LDPC}}}}&{}&{L_{1,Q}^{{\rm{LDPC}}}}\\ {L_{2,1}^{{\rm{LDPC}}}}&{L_{2,2}^{{\rm{LDPC}}}}& \cdots &{L_{2,Q}^{{\rm{LDPC}}}}\\ {}& \vdots &{}&{}\\ {L_{K,1}^{{\rm{LDPC}}}}&{L_{K,2}^{{\rm{LDPC}}}}&{}&{L_{K,Q}^{{\rm{LDPC}}}} \end{array}} \right] $ |
4) 将K个用户LDPC译码器译码后的似然比软信息矩阵减去LDS多用户检测器传递给LDPC译码器的软信息矩阵LLDS,得到LDPC译码器回传给LDS检测器的软信息矩阵
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{L}}^{{\rm{LDPC}} \to {\rm{LDS}}}} = {\mathit{\boldsymbol{L}}^{{\rm{LDPC}}}} - {\mathit{\boldsymbol{L}}^{{\rm{LDS}}}} = }\\ {\left[ {\begin{array}{*{20}{c}} {L_{1,1}^{{\rm{LDPC}} \to {\rm{LDS}}}}&{L_{1,2}^{{\rm{LDPC}} \to {\rm{LDS}}}}&{}&{L_{1,Q}^{{\rm{LDPC}} \to {\rm{LDS}}}}\\ {L_{2,1}^{{\rm{LDPC}} \to {\rm{LDS}}}}&{L_{2,2}^{{\rm{LDPC}} \to {\rm{LDS}}}}& \cdots &{L_{2,Q}^{{\rm{LDPC}} \to {\rm{LDS}}}}\\ {}& \vdots &{}&{}\\ {L_{K,1}^{{\rm{LDPC}} \to {\rm{LDS}}}}&{L_{K,2}^{{\rm{LDPC}} \to {\rm{LDS}}}}&{}&{L_{K,Q}^{{\rm{LDPC}} \to {\rm{LDS}}}} \end{array}} \right] = }\\ {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{L}}_1^{{\rm{LDPC}} \to {\rm{LDS}}}}\\ {\mathit{\boldsymbol{L}}_2^{{\rm{LDPC}} \to {\rm{LDS}}}}\\ \vdots \\ {\mathit{\boldsymbol{L}}_K^{{\rm{LDPC}} \to {\rm{LDS}}}} \end{array}} \right]} \end{array} $ |
将该矩阵回传给多用户检测器.
5) 类似1),多用户检测器进行Q次多用户检测,不同之处在于MP算法第1次迭代时变量节点的软信息不再为0,而是LDPC译码器回传的软信息.如在第q次检测时以矩阵LLDPC→LDS的第q列作为迭代检测中第1步迭代时的外信息,则LVk→Fn(0)=Lk, qLDPC→LDS.此后的迭代中
6) 类似2),将LDS多用户检测器的输出LLDS传递给LDPC码译码器.
7) 类似3),进行LDPC码译码. 4)~7) 完成1次LDS与LDPC码联合检测译码的外迭代.当外迭代数达到最大值M时转8),否则转4) 继续进行检测译码.
8) 对K个用户的LDPC译码器的输出进行判决
图 1为联合迭代检测译码算法的方框图,其中,yq=[yq, 1 yq, 2 … yq, N]T(q=1, 2, …, Q)表示信道输出的扩展符号序列.
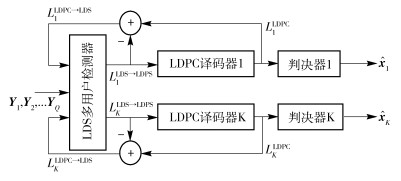
|
图 1 联合检测译码迭代算法方框图 |
对LDS和LDPC码联合检测译码迭代算法的性能进行仿真.仿真中,LDPC码采为码率为0.5的(1008, 504) 规则码;调制方式采用BPSK;按照van de Beek等[6]中提出的准则设计S矩阵;LDS系统的负载分别为133%、167%和200%,3种负载时S矩阵的dv均为3,dc分别为4、5、6.
图 2所示为3种系统负载下,不同外迭代次数时所有用户误比特率(BER, bit error rate)平均值.同时也仿真了单用户时采用同样的LDPC编码及相同译码迭代次数下的误比特率作为比较基准.仿真中,LDS多用户检测和LDPC码译码的总迭代次数分别固定为24和100次,外迭代1、2、3、4次时每次LDS多用户检测和LDPC码译码的内迭代次数分别为12和50次、8和33次、6和25次、5和20次.
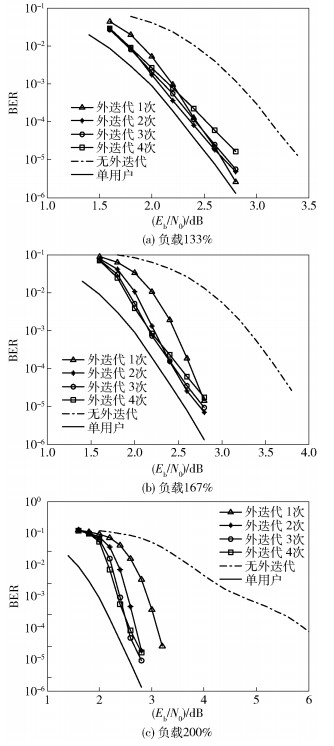
|
图 2 不同外迭代次数时的误比特率 |
从仿真结果可以看出,联合迭代算法对误码性能的改善非常明显,系统负载越高,改善越大.即使是只进行1次外迭代,在BER为10-4时,系统负载133%、167%和200%时的误码性能分别改善了0.7 dB、1.0 dB和2.8 dB.从联合外迭代次数对误码性能的影响来看,整体上看外迭代次数较多时性能较好.在系统负载为133%和167%时,外迭代2~4次的性能相近,在高信噪比时外迭代4次的性能要稍差;在负载为200%时,外迭代3次和4次的性能相近,在高信噪比时,外迭代4次时的性能要比迭代3次时稍差.外迭代次数增加时,每次LDS多用户检测和LDPC码译码的内迭代次数相应减少,在信噪比较高时LDS检测和LDPC码的译码收敛程度较低,导致性能较差.而在负载较高、用户数较多时,用户间干扰更大,多用户检测和LDPC码间多次联合迭代带来的性能改善非常明显,不仅补偿了内迭代次数减少带来的性能损失,还带来更多的性能改善. 图 2的仿真结果说明,联合外迭代的次数设置为2~3次较为适当,此时的误码性能与单用户时相差已不大,设置更多的外迭代次数会导致每次内迭代的次数过少,反而对高信噪比时的性能改善不利.
图 3为不同系统负载下,性能最好用户和性能最差用户的误比特率,以及所有用户误比特率的平均值的比较图.需要说明的是,仿真中性能最差用户和最好用户是随机的且图例表示所有带符号的实线为外迭代3次,带符号的虚线为无外迭代.仿真中,多用户检测迭代次数为6,译码迭代次数为25,外迭代次数为3.从图中可以看出,不进行联合外迭代时,用户间性能存在较大差异,系统负载越大,差异越大.而采用多用户检测与LDPC译码联合外迭代后,用户间的性能差异明显缩小,而且负载越大,差异越小.这是因为通过将LDPC码译码后的软信息再反馈给LDS多用户检测器,可靠度高的用户能有效帮助提高可靠度较低的用户符号的可靠度,复用的用户越多,用户间的相互影响越大,相互间的帮助也越大,通过外迭代带来的性能改善越大.且图例表示为所有带符号的实线为外迭代3次,带符号的虚线为无外迭代.
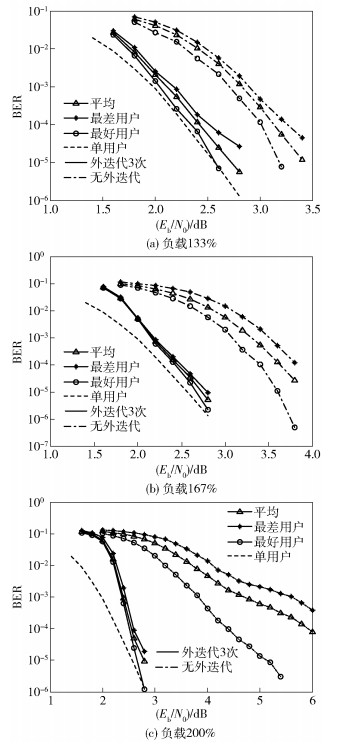
|
图 3 采用联合迭代检测译码算法的用户性能比较 |
为了比较不同负载下的误比特率,将图 2中3种负载下不进行联合外迭代和进行3次联合外迭代的误比特率曲线绘制到了同一个图中,如图 4所示.从图中可以看出,系统负载越大,误码性能越差,这是因为复用的用户数增加使用户间的干扰增大.而进行联合外迭代时3种负载下的误码性能差距明显小于不进行外迭代时.原因在于进行检测和译码联合外迭代后,用户数量越多,用户间消息传递带来的性能改善越明显,因此减轻了因用户间干扰增加带来的性能下降程度.在误比特率为10-4时,与独立进行检测和译码相比,3种负载情况下,联合检测译码迭代算法系统性能改善分别达到0.7、1.2和3.3 dB.
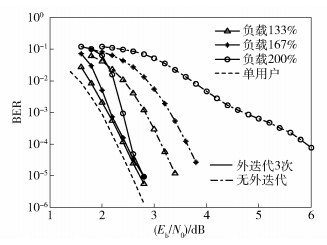
|
图 4 不同系统负载下联合迭代检测译码算法性能比较 |
图 5为不同多用户检测和译码内迭代次数对系统性能影响的仿真结果.仿真中系统负载为167%.仿真的4种内迭代次数分别为12和40次、18和60次、24和100次、30和120次.联合迭代时外迭代次数都为2.可见,总迭代次数增加时,检测和译码分开进行的性能改善较小,而检测和译码联合进行的改善较大.这是因为后者每次检测和译码的内迭代次数较少,增加迭代次数对性能的改善更明显.图中还可以看到,联合迭代时,多用户检测迭代和LDPC译码迭代次数分别从18和60次增加到20和100次时系统性能有较明显的改善,但再增加到30和120次时则改善已不明显.综合系统性能与计算复杂度两方面考虑,多用户检测总迭代次数24、LDPC码译码总迭代次数100两种迭代方案较为合理.

|
图 5 不同迭代总数对系统性能的影响 |
研究了LDS非正交多址系统中多用户检测与信道编码译码联合迭代的方案.将多用户检测和LDPC码的译码进行联合迭代,在不同系统负载下,对不同的多用户检测、LDPC码译码内迭代次数,以及不同的联合外迭代次数下的误比特率进行了仿真,同时也仿真了相同条件下多用户检测和LDPC码译码单独进行时的误比特率,以及无用户间干扰时的误比特率.仿真结果表明,在多用户检测迭代总次数和LDPC译码迭代总次数相同的情况下,给出的检测和译码联合迭代算法明显改善了误码性能,而复用的用户数越多,性能改善越大,误码性能已经非常接近单用户时的性能.同时,采用联合迭代算法后,不同用户间的性能差异也明显减小.提出算法在没有增加计算复杂度的情况下,明显改善了LDS系统的误码性能,具有较好的实用价值.
| [1] | Dai Linglong, Wang Bichai, Yuan Yifei, et al. Non-orthogonal multiple access for 5G:solutions, challenges, opportunities, and future research trends[J]. IEEE Communications Magazine, 2015, 53(9): 74–81. doi: 10.1109/MCOM.2015.7263349 |
| [2] | Ma Zheng, Zhang Zhengquan, Ding Zhiguo, et al. Key techniques for 5G wireless communications:network architecture, physical layer, and MAC layer perspectives[J]. Science China:Information Sciences, 2015, 58(4): 1–20. |
| [3] | Saito Y, Kishiyama Y, Benjebbour A, et al. Non-orthogonal multiple access (NOMA) for cellular future radio access[C]//2013 IEEE 77th Vehicular Technology Conference (VTC). Dresden:IEEE Press, 2013:1-5. |
| [4] | Benjebbour A, Saito Y, Kishiyama Y, et al. Concept and practical considerations of non-orthogonal multiple access (NOMA) for future radio access[C]//2013 International Symposium on Intelligent Signal Processing and Communications Systems (ISPACS). Naha:IEEE Press, 2013:770-774. |
| [5] | Hoshyar R, Wathan F P, Tafazolli R. Novel low-density signature for synchronous CDMA systems over AWGN channel[J]. IEEE Transactions on Signal Processing, 2008, 56(4): 1616–1626. doi: 10.1109/TSP.2007.909320 |
| [6] | Van de Beek J, Popovic B M. Multiple access with low-density signatures[C]//IEEE Global Communication Conference (GLOBECOM). Honolulu:IEEE Press, 2009:1-6. |
| [7] | Hoshyar R, Razavi R, AL-Imari M. LDS-OFDM:an efficient multiple access technique[C]//2010 IEEE 71st Vehicular Technology Conference (VTC). Taipei:IEEE Press, 2010:1-7. |
| [8] | Du Yang, Dong Binhong, Gao Pengyu, et al. Low-complexity LDS-CDMA detection based on dynamic factor graph[C]//2016 IEEE Global Communication Workshops (GC Wkshps). Washington, DC:IEEE Press, 2016:1-6. |
| [9] | Safavi A R, Perotti A G, Popovic B M. Ultra low density spread transmission[J]. IEEE Communications Letters, 2016, 20(7): 1373–1376. |
| [10] | Nikopour H, Baligh H. Sparse code multiple access[C]//2013 IEEE 24th International Symposium on Personal Indoor and Mobile Radio Communications (PIMRC). London:IEEE Press, 2013:332-336. |
| [11] | Zeng Jie, Li Bing, Su Xin, et al. Pattern division multiple access (PDMA) for cellular future radio access[C]//2015 International Conference on Wireless Communications & Signal Processing (WCSP). Nanjing:IEEE Press, 2015:1-5. |
| [12] | Kong Dan, Zeng Jie, Su Xin, et al. Multiuser detection algorithm for PDMA uplink system based on SIC and MMSE[C]//2016 IEEE/CIC International Conference on Communications in China (ICCC). Chengdu:IEEE Press, 2016:27-29. |
| [13] | Kopbayashi M, Boutros J, Caire G. Successive interference cancellation with SISO decoding and EM channel estimation[J]. IEEE Journal on Selected Areas in Communications, 2006, 19(8): 1450–1460. |


