2. 河南理工大学 计算机科学与技术学院, 河南 焦作 454000
传统的能量感知算法对噪声比较敏感,在较低的信噪比条件下检测准确性易受到影响,循环特征检测法计算复杂度偏高,为此提出了基于能量检测和小波变换(WT)感知的双门限联合检测算法.该算法对双门限区间以外的区域采用能量检测进行判定,双门限范围内的不确定区域进行小波感知,并根据信道中噪声不确定性自适应调整双门限值,当信道质量较好时,减小两门限之间的距离,否则增大两门限之间的距离,从而控制进行小波感知的概率.仿真结果表明,此算法有效地提高了低信噪比条件下系统的检测性能,降低了算法的复杂度.
2. School of Computer Science and Technology, Henan Polytechnic University, Henan Jiaozuo 454000, China
Considering that the traditional energy detection algorithm is sensitive to noise, the detection accuracy is easy to be affected in low signal-to-noise ratio (SNR) conditions, and that cyclostationary detection algorithm is high computing complexity, a double-threshold joint detection algorithm based on energy detection and wavelet transform (WT) sensing was proposed. When the decision statistic falls outside the double-threshold section, the energy detection is performed and the confused region is within the double-threshold for wavelet detection. Besides, the two thresholds can be adjusted adaptively according to noise uncertainty. When the channel quality is better, the distance of the two thresholds will be minished, otherwise the distance of the two thresholds will be larger, so as to control the probability of wavelet detection. Simulation shows that the proposed algorithm can improve the detection performance effectively under low SNR conditions, and reduces the complexity.
随着无线通信系统的迅速发展,用户对频谱资源的需求日益增长,而传统的静态频谱管理方式造成了严重的频谱资源浪费,使现有的频谱资源未能充分利用.认知无线电(CR, cognitive radio)作为解决频谱资源紧缺的重要手段,在不影响主用户(PU, primary user)正常通信的情况下,次用户(SU, secondary user)通过感知时域、频域、空域上的频谱空穴,机会地接入授权频段进行数据传输,以实现对现有频谱的合理利用,达到提高频谱利用率的目的[1-2].常用的本地频谱感知方法有能量检测算法[3]、匹配滤波器检测算法、循环平稳特征检测算法等,及在此基础上的联合分步频谱感知算法[4].能量感知虽简单易于实现但不能区分信号和噪声,易受噪声不确定性影响,在低信噪比(SNR, signal-to-noise ratio)条件下检测性能较差.匹配滤波器感知虽然为理论上较优的信号检测方法,但需要主用户在物理层和介质访问控制(MAC, media access control)层的先验知识,在复杂多变的无线环境下难以实施.循环平稳感知在较低的SNR下仍具有很好的检测性能但却存在计算复杂度高、时延大的缺点[5].为提高在低信噪比下的频谱检测性能,降低算法复杂度,结合小波变换(WT, wavelet transform)[6]感知在低信噪比条件下具有良好的检测性能和较低的运算复杂度,以能量检测为基础,提出基于能量检测和小波变换感知的双门限联合频谱感知算法,第1步对信号进行能量检测,若能量值X大于高门限λH时则判定授权用户存在,若能量值X小于低门限λL时则判定授权用户不存在,如果能量值介于两个门限之间则进行第2步精细感知,即进行基于小波变换的频谱感知,做出最终判决.
1 检测模型与能量检测在认知无线电网络中,用下面的数学二元检测模型来检测PU信号
| $ x\left( n \right) = \left\{ \begin{array}{l} w\left( n \right),{H_0}\\ s\left( n \right)h\left( n \right) + w\left( n \right),{H_1} \end{array} \right. $ | (1) |
其中:x(n)为认知用户(SU)接收到的信号,s(n)为授权用户(PU)发射信号, w(n)~N(0, δw2)表示均值为0, 方差为δw2的加性高斯白噪声(AWGN,additive white gaussian noise), h(n)表示认知用户和授权用户之间的信道增益. H0表示主用户信号不存在,反之H1表示主用户信号存在.
能量检测的原理结构如图 1所示.

|
图 1 能量检测 |
能量检测算法判决统计量为
| $ X = \frac{1}{N}\sum\limits_{n = 1}^N {{{\left| {x\left( n \right)} \right|}^2}} $ | (2) |
其中N为接收输入信号采样数量.传统单门限能量检测的虚警概率Pf和检测概率Pd分别表示为[7]
| $ {P_{\rm{f}}} = P\left\{ {X > \lambda \left| {{H_0}} \right.} \right\} = Q\left( {\frac{{\lambda - N\delta _w^2}}{{\sqrt {2N\delta _w^4} }}} \right) $ | (3) |
| $ {P_{\rm{d}}} = P\left\{ {X > \lambda \left| {{H_1}} \right.} \right\} = Q\left( {\frac{{\lambda - N\left( {\delta _s^2 + \delta _w^2} \right)}}{{\sqrt {2N{{\left( {\delta _s^2 + \delta _w^2} \right)}^2}} }}} \right) $ | (4) |
其中:
| $ \lambda = {Q^{ - 1}}\left( {{{\bar P}_{\rm{f}}}} \right) \times \sqrt {2N\delta _w^4} + N\delta _w^2 $ | (5) |
其中,λ为设置的单门限值,若X≥λ, 则判决授权用户存在,若X<λ, 则判决授权用户不存在.由于受到周围信道环境变化的影响,单门限能量检测很容易造成误判,局限性较大.
2 小波感知检测 2.1 系统架构及分析假设信道中的噪声是均值为0, 方差为δw2的高斯白噪声,较真实地反映了信道环境的噪声特性.根据信号和噪声在小波域里面有着不同的统计特性,噪声在不同的小波尺度上有一致的特征,而信号为非一致分布的,将信号和噪声分离,经过小波去噪算法从而判断PU信号是否存在.小波变换感知能在一个低信噪比的环境下,不需要主用户先验知识的情况下正确识别信号. 图 2所示为小波变换感知系统架构.

|
图 2 小波感知系统架构 |
其中,对经过带通滤波器后的采样信号x(n),进行归一化得
| $ G\left( n \right) = \frac{{x\left( n \right)}}{{{\rm{sum}}\left[ {{\rm{abs}}\left( {x\left( n \right)} \right)/{\rm{length}}\left( {x\left( n \right)} \right)} \right]}} $ | (6) |
其中:sum()表示求和运算,abs()为求绝对值运算,length()为求序列长度,然后对G(n)进行Daubechies 4(db4) 小波变换[8-9].
在db4小波变换中,在i-th时间和j-th频率的小波系数表示如下
| $ W\left( {i,j} \right) = \int_{ - \infty }^{ + \infty } {{2^{ - \frac{j}{2}}}x\left( t \right)\psi \left[ {{2^{ - i}}\left( {t - j} \right)} \right]{\rm{d}}t} $ | (7) |
其中ψ()为小波窗函数,经过小波变换后信号的小波系数幅值要大于噪声的小波系数幅值.通过设置合适的阈值去除噪声产生的小波系数保留有用信号的小波系数,从而达到去除噪声的目的.
2.2 小波去噪决策算法小波去噪判决算法,使用信号在小波去噪过程中的变化尺度来作为判决参数,经过小波去噪后,如果有轻微的波形振幅变化则说明为主用户信号,如果去噪前后变化非常明显则说明为噪声信号[10].
根据Donoho等提出的小波阈值去噪理论[11],在大样本条件下,噪声的小波系数的幅值都不会大于
| $ \mathop {\lim }\limits_{n \to \infty } P\left( {\mathop {\max }\limits_{0 \le j \le n} \left| {W\left( {i,j} \right)} \right| \le \mathit{\Gamma }} \right) = 1 $ | (8) |
其中,W(i, j)为噪声小波系数,采用硬阈值去噪法[12-13],将低于阈值的小波系数置零,高于阈值的小波系数保持不变.经过去噪后的小波系数为
| $ \hat W\left( {i,j} \right) = \left\{ \begin{array}{l} W\left( {i,j} \right),\left| {W\left( {i,j} \right)} \right| \ge \mathit{\Gamma }\\ 0,\left| {W\left( {i,j} \right)} \right| < \mathit{\Gamma } \end{array} \right. $ | (9) |
滤除噪声的小波系数,定义判决函数Z=|Gw(n)|,Gw(n)=WTD(G(n))=
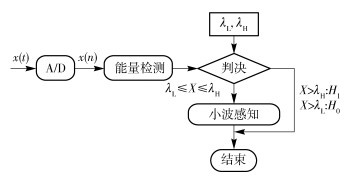
自适应双门限联合频谱感知的基本原理结构如图 3所示.
|
图 3 自适应双门限联合感知 |
首先对采样x(n)信号进行能量检测,若累积能量X>λH则认为所选频谱被占用即判为H1;若X<λL则认为所选频谱空闲判为H0;若λL≤X≤λH,即判决统计计量落在不确定区域C,则利用能量检测无法判决所选频谱的占用状态,此时则对采样信号进行小波变换频谱感知.从而解决了单门限能量检测造成感知失败的问题,并提高了低信噪比下的检测准确度.
双门限联合检测判决如下:
| $ \begin{array}{l} {H_0}:X < {\lambda _{\rm{L}}}\\ {H_x}:{\lambda _{\rm{L}}} \le X \le {\lambda _{\rm{H}}}\\ {H_1}:X > {\lambda _{\rm{H}}} \end{array} $ | (10) |
若判为Hx,则进行小波感知,其联合检测性能表示为
| $ \begin{array}{*{20}{c}} {{P_{\rm{d}}} = P\left( {X > {\lambda _{\rm{H}}}\left| {{H_1}} \right.} \right) + P\left( {{\lambda _{\rm{L}}} \le X \le {\lambda _{\rm{H}}}\left| {{H_x}} \right.} \right){P_{{\rm{dw}}}} = }\\ {P\left( {X > {\lambda _{\rm{H}}}\left| {{H_1}} \right.} \right) + P\left( {{\lambda _{\rm{L}}} \le X \le {\lambda _{\rm{H}}}\left| {{H_x}} \right.} \right)P\left( {Z > T\left| {{H_1}} \right.} \right)} \end{array} $ | (11) |
| $ \begin{array}{*{20}{c}} {{P_{\rm{f}}} = P\left( {X > {\lambda _{\rm{H}}}\left| {{H_0}} \right.} \right) + P\left( {{\lambda _{\rm{L}}} \le X \le {\lambda _{\rm{H}}}\left| {{H_x}} \right.} \right){P_{{\rm{fw}}}} = }\\ {P\left( {X > {\lambda _{\rm{H}}}\left| {{H_0}} \right.} \right) + P\left( {{\lambda _{\rm{L}}} \le X \le {\lambda _{\rm{H}}}\left| {{H_x}} \right.} \right)P\left( {Z > T\left| {{H_0}} \right.} \right)} \end{array} $ | (12) |
图 4表示主用户信号和噪声的能量分布,其中在λH和λL之间主用户信号和噪声交叉的区域为不确定区域C,若能量值X落在该区域则无法准确判决主用户信号是否存在则进行第2步判决.若能量值X落在H0区域表示主用户信号不存在,落在H1区域则表示存在主用户信号.

|
图 4 主用户信号和噪声能量分布 |
假设无线环境的噪声不确定性为[δw2/ρ, ρδw2], 其中ρ≥1是量化的不确定性参数,根据恒虚警检测理论由式(3) 可推导出
| $ {\lambda _{\rm{H}}} = {Q^{ - 1}}\left( {{{\bar P}_{\rm{f}}}} \right) \times \sqrt {2N\rho \delta _w^4} + N\rho \delta _w^2 $ | (13) |
| $ {\lambda _{\rm{L}}} = {Q^{ - 1}}\left( {{{\bar P}_{\rm{f}}}} \right) \times \sqrt {2N\delta _w^4/\rho } + N\delta _w^2/\rho $ | (14) |
其中:Q-1()表示高斯标准高斯互补累积函数的逆函数,Pf为目标虚警概率.所使用的双阈值能量检测,上限阈值λH和下限阈值λL的选取分别根据最大噪声方差和最小噪声方差,并根据信道状态自适应调整门限值,当信道状态较差时,则通过增大ρ值,适当地增大λL,λH之间的距离,否则就减小ρ值,当信道质量足够好时,甚至令ρ=1,此时λL=λH=λ实行单门限能量检测,令Δ=10lgρ为模拟的信噪比步长,为了避免太过频繁地调整门限,设置预期检测概率Pd,并引入概率调整因子0<θ<0.5, 当实际检测概率高于Pd(1+θ)或低于Pd(1-θ)时才进行调整,若检测概率在两者之间则不进行调整.
3.3 算法流程1) 初始化,根据式(13) 和(14) 计算出λL, λH.并利用式(2) 计算出判决统计量X.
2) X与判决门限进行比较,若X>λH, 则判决为H1, 若X<λL, 则判决为H0.
3) 若λL≤X≤λH,则判定为Hx, 进行第2步感知, 若Z>T则判决为H1, 若Z<T, 则判决为H0.
4) 根据式(11) 和(12) 计算出实际检测概率Pd和虚警概率Pf.
5) 如果Pd<Pd(1-θ),Δ增加0.5 dB,由此来调整门限值.
6) 如果Pd(1-θ)≤Pd≤Pd(1+θ), Δ保持不变,门限值不进行调整.
7) 如果Pd>Pd(1+θ),将Δ减小0.5 dB,进行门限调整,至此本次循环结束,转到第1步.
4 仿真分析为验证算法的有效性,采用蒙特卡罗仿真方法,进行仿真实验,来分析所提频谱感知算法的性能.假设信道噪声为AWGN,接收信号采用BPSK调制信号,信号带宽Wb=5×104, 设置采样点N=1 024, 仿真次数为5 000.
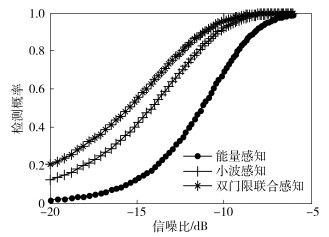
图 5为在一定的虚警概率Pf=0.01下,3种频谱感知算法的检测性能随信噪比变化的受试者工作特征曲线(ROC, receiver operating characteristic curve),在低信噪比的条件下,与简单的能量检测相比,小波感知在很大程度上改善了Pf和Pd,显著提高检测精度14 dB.通过比较分析,双门限联合频谱感知算法与其他两种感知方法相比有较高的检测概率,并且虚警概率维持在一个较低的水平.
|
图 5 不同SNR下3种检测方法性能ROC曲线 |
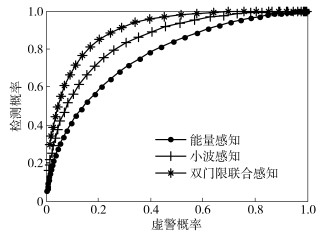
图 5不同SNR下3种检测方法性能ROC曲线图 6所示为SNR为-15 dB时,不同的虚警概率与检测概率的关系,由图可以看出,当虚警概率在一定的区间范围内,双门限联合频谱感知算法的检测概率明显高于传统能量检测和小波感知,当Pf=0.1时,检测概率Pd约为0.75,在一定的信噪比下检测概率Pd随着虚警概率Pf的增大而增大.
|
图 6 检测概率随虚警概率变化ROC曲线 |
图 7所示为不同数量的采样点N,算法的计算次数比较曲线,通过分析可知,双门限联合频谱感知的算法运算量为Ο=ΟE+P(λL≤X≤λH|Hx)ΟW,其中ΟE、ΟW分别为进行能量检测和小波检测的运算次数.可以看出,随着采样点数N的增加,各算法的运算次数呈不同程度的增加,但在一定采样条件下,所提的双门限联合感知的运算次数要远低于循环特征检测和小波感知.对算法复杂度进行分析,小波感知的算法复杂度为O(N),低于循环特征检测的算法复杂度O(N2).双门限联合频谱感知的算法复杂度介于能量感知和小波感知之间,低于循环特征检测和小波感知算法.

|
图 7 算法复杂度ROC曲线 |
针对能量检测在低信噪比条件下,检测准确性较差,提出了一种基于能量检测和小波变换感知的双门限联合频谱感知算法,该算法结合了能量检测和小波感知的优点,并根据信道状态,自适应调整两门限值采用不同的感知策略,从而减少了误判.仿真结果表明,算法明显改善了低信噪比条件下的检测性能,并降低了算法的运算复杂度.
| [1] | Haykin S. Cognitive radio:brain-empowered wireless communications[J]. IEEE Journal on Selected Areas in Communications, 2005, 23(2): 201–220. doi: 10.1109/JSAC.2004.839380 |
| [2] | Ghasemi A, Sousa E S. Spectrum sensing in cognitive radio networks:requirements, challenges and design trade-offs[J]. IEEE Communications Magazine, 2008, 46(4): 32–39. doi: 10.1109/MCOM.2008.4481338 |
| [3] | Lopez-Benitez M, Casadevall F. Improved energy detection spectrum sensing for cognitive radio[J]. IET Communications, 2012, 6(8): 785–796. doi: 10.1049/iet-com.2010.0571 |
| [4] | Sesham S, Sabat S L. Spectrum Sensing for Cognitive Radio Networks[C]//White Space Communication.[S.l.]:Springer International Publishing, 2015:117-151. |
| [5] | Tan Xiaobo, Zhang Hang. A CORDIC-Jacobi based spectrum sensing algorithm for cognitive radio[J]. KSⅡ Transactions on Internet & Information Systems, 2012, 6(9): 1998–2016. |
| [6] | Zhao Yu, Wu Yuanyuan, Wang Jian, et al. Wavelet transform for spectrum sensing in cognitive radio networks[C]//2014 International Conference on Audio, Language and Image Processing. Shanghai:IEEE, 2014:565-569. |
| [7] | Bagwari A, Kanti J, Tomar G, et al. A robust detector using SNR with adaptive threshold scheme in cognitive radio networks[J]. International Journal of Signal Processing, Image Processing and Pattern Recognition, 2016, 9(5): 173–186. doi: 10.14257/ijsip |
| [8] | Tian Z, Giannakis G B. A wavelet approach to wideband spectrum sensing for cognitive radios[C]//1st International Conference on Cognitive radio Oriented Wireless Networks and Communications. Mykonos Island:IEEE, 2006:1-5. |
| [9] | Li Haiyue, Li Jing. Wavelet transforms detection of spectrum sensing in the space network[C]//Science and Information Conference. London:IEEE, 2015:978-984. |
| [10] | Zhao Yu, Guo Bin. Cognitive Radio spectrum sensing based on wavelet denoising[M]. Heidelberg: Springer, 2012: 535-540. |
| [11] | Wang Haijun, Xu Yi, Su Xin, et al. Cooperative spectrum sensing with wavelet denoising in cognitive radio[C]//2010 IEEE 71st Vehicular Technology Conference. Taipei:IEEE, 2010:1-5. |
| [12] | Graps A. An introduction to wavelets[J]. IEEE Computational Science & Engineering, 1995, 2(2): 50–61. |
| [13] | Mallat S G. A theory for multiresolution signal decomposition:the wavelet representation[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2010, 11(7): 674–693. |


