基于45 GHz毫米波室内通信测量对木板、镜子以及白铁板的阻挡绕射特性进行了研究.根据阻挡物材料的不同,分别提出三射线和四射线阻挡绕射模型.对12 mm厚的木板、6 mm厚的镜子以及0.35 mm厚的白铁板进行了矩形阻挡绕射测量实验.实验结果表明,在矩形木板阻挡下45 GHz毫米波的平均传输衰减系数约为-4.28 dB,其衰减测量结果与提出的四射线模型仿真结果平均误差为-0.02 dB.在0.35 mm厚的矩形白铁板阻挡下,45 GHz毫米波的平均传输衰减系数约为-18.2 dB.在镜子远离天线的情况下,面对发射天线时的平均传输衰减比背对发射天线时大1~2 dB,而在镜子靠近天线的情况下,其面对发射天线时测量的结果与白铁板阻挡下的衰减类似.
The block diffraction attenuation characteristics of wood board, mirror and white iron board were studied based on 45 GHz millimeter wave indoor communication measurements. According to different block material, the 3-ray and 4-ray block diffraction models were proposed, respectively. The rectangular block diffraction measurement experiments were carried out on 12 mm thick wood board, 6mm thick mirror, and 0.35 mm thick white iron board. Experiment shows that the average transmission attenuation coefficient of 45 GHz millimeter wave blocked by 12 mm thick rectangular wood board is about -4.28 dB, and the average error between the attenuation measurement results and the 4-ray model simulation results is about -0.02 dB. The average transmission attenuation coefficient of 45 GHz millimeter wave blocked by 0.35 mm thick rectangular white iron board is about -18.2 dB. In the case of the mirror far away from the antennas, the measured average transmission attenuation by the mirror surface is 1-2 dB larger than that of the negative one. When the mirror is near any set of antennas, the measured value by the mirror surface is similar to that of the white iron board.
目前移动通信有限的频带已经制约了通信速率的进一步提高.寻求新的频谱资源使蜂窝通信系统的容量在未来十年增长1 000倍[1-2], 达到吉比(Gb)高速数据通信的目标,是下一代移动通信要解决的主要问题[3].毫米波频段有丰富的频率资源可供开发利用,其百分之一的相对带宽即可提供上千兆的通信带宽[4].蔡等[5]研究了mm-wave WPAN相关技术.邹等[6]对60 GHz无线通信波束赋形码本设计做了相关报道.陈等[7]基于小波分析对毫米波瞬态信号特征矢量的提取进行了研究.针对电磁波在刃型模型、楔形模型等阻挡下的绕射性能,Vogler[8]进行了相关理论推导.
针对不同的阻挡材料,分别提出三射线和四射线2种建模方案,并对2种模型进行了理论仿真.在室内45 GHz毫米波下进行了阻挡绕射衰减测量实验.根据测量结果,计算了45 GHz毫米波在几种阻挡下的平均传输衰减系数,并将模型的仿真结果和实验测量数据进行了比较,分析了模型的精度.
1 实验测量环境45 GHz毫米波矩形阻挡测量实验是在一个带有生产车间的实验室内进行的,图 1所示为实验测量场景.从图 1可以发现,在视线(LOS,line of sight)信道的周围存在着很多家具、支撑柱以及设备,这些设施都会给毫米波信号带来不同程度多径反射.测量过程中发射天线(TX)和接收天线(RX)均采用定向喇叭天线,天线之间的距离为8 m.矩形阻挡物分别采用木板、镜子以及白铁板3种不同的材料.实验系统的参数配置如表 1所示.

|
图 1 实验测量场景 |
|
|
表 1 45 GHz矩形阻挡模型测量系统参数配置 |
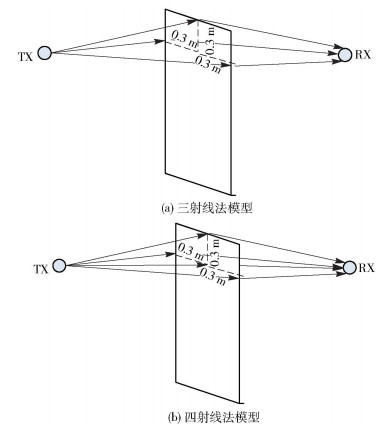
根据矩形阻挡物材料的不同,分别提出三射线和四射线建模的方案.铁的相对介电常数和磁导率都很大,毫米波信号在铁板的阻挡下将会产生非常大的传输损耗,可以认为毫米波信号无法穿透铁板,所以对铁板阻挡采用三射线刃型绕射法建模.而对于比较薄的绝缘体材料,如木板,它的穿透损耗并不是非常大,在4~5 dB之间[9],所以采用四射线法建模.四射线包括三条刃型边缘绕射路径和一条透射路径. 2种模型如图 2所示.
|
图 2 针对不同阻挡材料的2种绕射模型 |
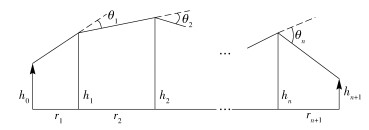
Vogler[8]提出了一个多重刃型边缘绕射模型计算方法,其几何模型如图 3所示.
|
图 3 Vogler法多重刃型边缘绕射几何模型 |
θ1,θ2,…,θn是绕射角,r1,r2,…,rn+1是多个刃型之间的间距,h1,h2,…,hn是刃型的高度,n是刃型的个数.根据前面介绍的几何量与无线电频率相结合,定义了两组参数αm和βm[8].
| $ {\alpha _m} = {\left[{\frac{{{r_m}{r_{m + 2}}}}{{\left( {{r_m} + {r_{m + 1}}} \right) \left( {{r_{m + 1}} + {r_{m + 2}}} \right)}}} \right]^{1/2}}, $ | (1) |
| $ {\beta _m} = {\theta _m}{\left[{\frac{{{\rm{i}}k{r_m}{r_{m + 1}}}}{{2\left( {{r_m} + {r_{m + 1}}} \right)}}} \right]^{1/2}}, m = 1, 2, \cdots, n $ | (2) |
其中:i是虚数,
信号传输过程中遇到多个刃型阻挡物时,计算绕射衰减场强E的表达式为
| $ \begin{align} & \ \ \ \ E=\left( 1/{{2}^{n}} \right){{C}_{n}}{{\text{e}}^{{{\sigma }_{n}}}}{{\left( 2/\sqrt{\pi } \right)}^{n}}\times \\ & \int_{{{\beta }_{1}}}^{\infty }{\cdots \int_{{{\beta }_{n}}}^{\infty }{{{\text{e}}^{2f}}\cdot {{\text{e}}^{-\left( x_{1}^{2}+x_{2}^{2}+\cdots +x_{n}^{2} \right)}}}}\text{d}{{\mathit{x}}_{\text{1}}}\cdots \text{d}{{\mathit{x}}_{\mathit{n}}} \\ \end{align} $ | (3) |
其中,
| $ f = \left\{ \begin{array}{l} 0, \;\;n = 1\\ \sum\limits_{m = 1}^{n - 1} {{\alpha _m}\left( {{x_m} - {\beta _m}} \right)} \left( {{x_{m + 1}} - {\beta _{m + 1}}} \right), n \ge 2 \end{array} \right. $ | (4) |
| $ {\sigma _n} = \beta _1^2 + \beta _2^2 \cdots + \beta _n^2 $ | (5) |
| $ {C_n} = \left\{ \begin{array}{l} 1, \;\;\;n = 1\\ {\left[{\frac{{{r_2}{r_3} \cdots {r_n}{r_{\rm{T}}}}}{{\left( {{r_1} + {r_2}} \right) \left( {{r_2} + {r_3}} \right) \cdots \left( {{r_n} + {r_{n + 1}}} \right)}}} \right]^{1/2}}\;\;n \ge 2 \end{array} \right. $ | (6) |
| $ {r_{\mathit{T}}} = {r_1} + {r_2} + \cdots + {r_{n + 1}} $ | (7) |
其中rT为发射机与第T个刃型之间的距离.当n=1时,就是单刃绕射模型,适合提出的方案,此时,式(3) 和式(2) 可以简化为下面2个式子.
| $ E=\frac{1}{2}{{\text{e}}^{\beta _{1}^{2}}}\frac{2}{\sqrt{\pi }}\int_{{{\beta }_{1}}}^{\infty }{{{\text{e}}^{-x_{1}^{2}}}\text{d}{{\mathit{x}}_{\text{1}}}} $ | (8) |
| $ {\beta _1} = {\theta _1}\sqrt {\frac{{{\rm{i}}k{r_1}{r_2}}}{{2\left( {{r_1} + {r_2}} \right)}}} $ | (9) |
毫米波的穿透性能很差,随着频率升高,穿透损耗会迅速增大,但这并不意味着毫米波就没有透射能力,其透射损耗与阻挡材料的介电常数、厚度等参数有关.信号透射示意如图 4所示[10].

|
图 4 信号透射示意图 |
图 4中的Pin为入射信号功率,Pout为透射信号功率,Pref为反射信号功率,D表示阻挡物的厚度.根据材料穿透的传输衰减可得
| $ \zeta = \left| {\frac{{\sqrt {{\varepsilon _{\rm{r}}}} - 1}}{{\sqrt {{\varepsilon _{\rm{r}}}} + 1}}} \right| $ | (10) |
其中εr为阻挡材料的相对介电常数. Pref与Pin以及Pout之间的关系可表示为
| $ \frac{{{\mathit{P}}_{\text{ref}}}}{{{P}_{\text{in}}}}={{\left| \zeta \right|}^{2}} $ | (11) |
| $ \frac{{{\mathit{P}}_{\text{out}}}}{{{P}_{\text{in}}}}={{\left( 1-{{\zeta }^{2}} \right)}^{2}}{{\text{e}}^{-2D\chi }} $ | (12) |
| $ \chi \approx \frac{\pi \text{tg}\delta }{\lambda \sqrt{{{\varepsilon }_{\text{r}}}}} $ | (13) |
其中:χ为衰落系数,λ为工作波长. tgδ为正切损耗角,则穿透损耗可以表示为
| $ A=-101\text{g}\left( {{\mathit{P}}_{\text{out}}}/{{\mathit{P}}_{\text{in}}} \right) $ | (14) |
公式的详细推导及举例计算请查看文献[10].根据文献[9-12]关于一些材料电气参数的报道,在表 2中整理了几种材料的电气参数,这些参数并不是在45 GHz下测量得到的,有一定误差,只能作为参考.
|
|
表 2 不同材料的电气特性参数表 |
下面将2种模型下仿真得到的结果与几种阻挡绕射衰减测量的结果进行分析比较.首先测出无阻挡情况下接收到的信号功率,将其作为基准.然后将矩形阻挡物从距离发射机0.5 m处开始向着接收机方向缓慢移动,每移动0.5 m记录一次接收到的信号功率,在每个测量点分别测量10组数据,取平均值作为该点的测量结果,从而减小随机误差.最后将矩形阻挡在不同位置时所接收到的信号功率与基准相减即为矩形阻挡产生的衰减.
3.1 木板阻挡实验与分析四射线法是针对木板等穿透损耗较小的绝缘体材料提出来的,本次实验对木板阻挡下的信号传输衰减进行了测量.直接把木板夹在收发天线之间测得45 GHz毫米波信号在12 mm木板中的穿透损耗约为-4.32 dB.从这个结果可知,木板对45 GHz毫米波的穿透损耗并不是很大,在研究其阻挡特性的时候,需要考虑透射的信号功率,而不能只考虑绕射信号功率.
根据文献[9],对于垂直极化波,不会发生全透射现象.采用四射线法对木板阻挡模型仿真时,在参数上选取90%的接收信号功率为透射信号,10%的接收信号功率为绕射信号进行理论仿真.仿真及实验测量结果如图 5所示.

|
图 5 木板阻挡下的衰减特性 |
图 5是木板阻挡下的实验测量结果以及四射线模型仿真曲线,两条曲线一致性较好,证明了针对木板阻挡采用四射线模型仿真时所选取的分配参数有效.测量得到的平均传输衰减系数约为-4.28 dB.实际测量到的信号功率衰减值与四射线模型理论仿真结果相比有一些误差,其误差分析如图 6所示.

|
图 6 木板测量与四射线模型仿真的误差 |
分析图 6可得,木板阻挡测量结果与四射线模型仿真结果的平均误差约为-0.02 dB,而且整体比模型仿真结果偏小,估计是系统误差引起的,可以通过提高测量系统的精度来减小测量误差.
比较实验结果与模型仿真结果可以证明45 GHz毫米波在被木板阻挡情况下,会同时出现透射和边缘绕射现象,而且接收到的信号功率是以透射信号为主.在给定的实验条件下,矩形木板阻挡物对45 GHz毫米波的平均传输衰减系数约为-4.28 dB,即大约只有37%的发射功率被接收天线收到.测量结果说明阻挡物对毫米波传输的影响是不可忽视的.
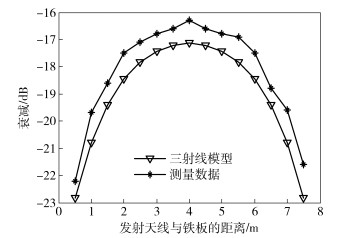
3.2 白铁板阻挡实验与分析提出三射线建模的方法来研究45 GHz毫米波在矩形良导体材料阻挡下的绕射性能.阻挡材料选择了0.35 mm厚的白铁板.模型仿真以及传输衰减测量结果如图 7所示.
|
图 7 矩形白铁板阻挡下的衰减特性 |
图 7是三射线模型的仿真曲线以及厚度为0.35 mm的矩形白铁板阻挡绕射测量曲线.实验中测量的信号绕射衰减比三射线模型仿真结果整体偏小,两者之间的误差曲线如图 8所示.

|
图 8 白铁板测量与三射线模型仿真的误差 |
分析图 8可知,矩形白铁板阻挡绕射实验测量与理论仿真的平均误差约0.83 dB,实验测量曲线有小的凸起.估计存在两方面的原因:1) 在白铁板阻挡下,到达接收天线的信号幅度很小,而在小信号接收情况下,系统误差较大,这种误差可以通过提高系统测量精度来改善. 2) 45 GHz毫米波在室内传输测量中存在多径传输现象,该现象与阻挡物的位置及周围环境等因素有关.
根据矩形白铁板阻挡绕射实验测量结果,可以求出在0.6 m×1.5 m矩形白铁板阻挡下,45 GHz毫米波的平均传输衰减系数约为-18.2 dB,即大约只有不到2%的发射功率被接收天线收到.
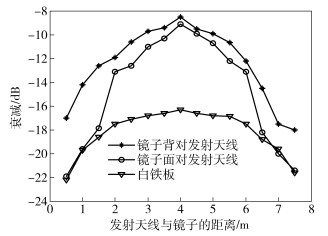
3.3 镜子阻挡实验与分析由于镜子的背面存在金属涂覆层,使其阻挡性能与玻璃有很大差异,对毫米波信号的阻挡衰减比玻璃大很多. 图 9是45 GHz毫米波信号在镜子面对发射天线和背对发射天线时的阻挡衰减测量结果与白铁板阻挡下的绕射衰减测量结果的对比.
|
图 9 镜子与白铁板测量数据比较 |
分析图 9可知,在远离收发天线的情况下(图 9中2~6 m之间),镜子面对发射天线时所测得的衰减比其背对发射天线时的衰减整体偏大约1~2 dB.然而,在镜子靠近发射天线和接收天线的各三个测量点,镜子面对发射天线情况下接收到的信号快速衰减,其衰减性能跟白铁板接近.而背对发射天线情况下测量到的信号衰减并没有出现剧烈变化.
根据图 9所示的实验测量结果可以求出,在0.6 m×1.5 m的矩形镜子背对发射天线的阻挡下,45 GHz毫米波的平均传输衰减系数约为-12.35 dB.而在镜子面对发射天线的阻挡下,45 GHz毫米波的平均传输衰减系数在其远离天线时与靠近天线时有很大差异.在远离天线的9个测量点其平均传输衰减系数约为-11.33 dB,而在靠近天线的6个点传输衰减系数约为-19.83 dB.
以上多种材料阻挡的实验测量结果表明,阻挡物对毫米波传输的影响是不可忽视的,在5 G系统设计中应予以重视.
4 结束语在45 GHz毫米波下针对不同材料的矩形阻挡,分别提出了三射线与四射线建模方法,并在实验室内对12 mm厚的木板、6 mm厚的镜子以及0.35 mm厚的白铁板进行了矩形阻挡测量实验.实验结果表明,在给定的实验条件下,矩形木板阻挡对45 GHz毫米波的平均传输衰减系数约为-4.28 dB,即大约只有37%的发射功率被接收天线收到.在白铁板阻挡下,45 GHz毫米波的平均传输衰减系数约为-18.2 dB,即大约只有不到2%的发射功率被接收天线收到.而镜子正反两面分别面对发射天线的测量结果有很大差别.在远离收发天线的测量点,两者的衰减值相差1~2 dB,而在靠近收发天线的各三个测量点,镜子面对发射天线时的衰减快速增大,其性能跟白铁板类似.实验结果对估计有矩形阻挡存在的5 G系统信道衰减特性有参考价值.
| [1] | Fettweis G, Alamouti S. 5G:Personal mobile internet beyond what cellular did to telephony[J]. IEEE Communications Magazine, 2014, 52(2): 140–145. doi: 10.1109/MCOM.2014.6736754 |
| [2] | Thompson J, Ge Xiaohu, Wu H-C, et al. 5G wireless communication systems:prospects and challenges[J]. IEEE Communications Magazine, 2014, 52(2): 62–64. doi: 10.1109/MCOM.2014.6736744 |
| [3] | Rappaport T S, MacCartney G R, Samimi M K, et al. Wideband millimeter wave propagation measurements and channel models for future wireless communication system design[J]. IEEE Transactions on Communications, 2015, 63(9): 3029–3056. doi: 10.1109/TCOMM.2015.2434384 |
| [4] |
王映洲, 李利军, 龚克. 毫米波室内传播特性的研究[J]. 电子学报, 1999, 27(3): 89–93.
Wang Yingzhou, Li Lijun, Gong Ke. A study on millimeter wave indoor propagation characteristics[J]. Acta Electronica Sinica, 1999, 27(3): 89–93. |
| [5] |
蔡冉, 刘丹谱. mm-wave WPAN中基于物理干扰模型的空间复用算法[J]. 北京邮电大学学报, 2013, 36(5): 19–24.
CAI Ran, LIU Dan-pu. Spatial sharing algorithm in mm-wave WPAN based on physical interference model[J]. Journal of Beijing University of Posts and Telecommunications, 2013, 36(5): 19–24. |
| [6] |
邹卫霞, 崔志芳, 李斌, 等. 基于N相位的60 GHz无线通信波束赋形码本设计方案[J]. 北京邮电大学学报, 2012, 35(3): 42–46.
ZOU Wei-xia, CUI Zhi-fang, LI Bin, et al. N phases based beamforming codebook design scheme for 60 GHz wireless communication[J]. Journal of Beijing University of Posts and Telecommunications, 2012, 35(3): 42–46. |
| [7] |
陈明奇, 杨义先. 毫米波瞬态信号的特征提取与识别[J]. 北京邮电大学学报, 1998, 21(4): 66–70.
Chen Mingqi, Yang Yixian. The feature extraction and recognition of millimeter wave transient signal[J]. Journal of Beijing University of Posts and Telecommunications, 1998, 21(4): 66–70. |
| [8] | Vogler L E. An attenuation function for multiple knife edge diffraction[J]. Radio Science, 1982, 17(6): 1541–1546. doi: 10.1029/RS017i006p01541 |
| [9] |
郭山红, 孙锦涛, 谢仁宏, 等. 电磁波穿透墙体的衰减特性[J]. 强激光与粒子束, 2009, 21(1): 113–117.
Guo Shanhong, Sun Jintao, Xie Renhong, et al. Attenuation characteristics of electromagnetic wave penetrating walls[J]. High Power Laser and Particle Beams, 2009, 21(1): 113–117. |
| [10] | 刘盛尧. 60 GHz毫米波无线信道传输特性硏究[D]. 北京: 华北电力大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10079-1015642547.htm |
| [11] | McDonnell J T E. Characteristics of the indoor wireless propagation environment at microwave and millimeter frequencies[C]//IEE Colloquium on Radio Communications at Microwave and Millimeter Wave Frequencies. London:IET Press, 1996:13/1-13/6. |
| [12] | Correia L M, Frances P O. Estimation of materials characteristics from power measurements at 60 GHz[C]//5th IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC'94). Hague:IEEE Press, 1994:510-513. |


