2. 哈尔滨工程大学 自动化学院, 哈尔滨 150001
针对传统卷积神经网络(CNN)模型构建过度依赖经验知识、参数多、训练难度大等缺点,同时鉴于复杂多类问题的CNN模型构建策略的重要价值,提出一种自适应深度CNN模型构建方法.首先,将初始网络模型的卷积层和池化层设置为仅含一幅特征图;然后,以网络收敛速度为评价指标,对网络进行全局扩展,全局扩展后,根据交叉验证样本识别率控制网络展开局部扩展,直到识别率达到预设期望值后停止局部网络学习;最后,针对新增训练样本,通过拓展新支路实现网络结构的自适应增量学习.通过图像识别实验验证了所提算法在网络训练时间和识别效果上的优越性.
2. College of Automation, Harbin Engineering University, Harbin 150001, China
The construction process of traditional convolutional neural network (CNN) model has many shortcomings, such as over reliance on experience knowledge, a lot of parameters and difficult to training. At the same time, in view of the important value of constructing strategy of CNN model in complex multi-class problems, a new construction method of adaptive deep CNN model was proposed. First, the convolution layer and pooling layer of the initial CNN model are set only to include one feature map; and then, the convergence rate of CNN is used as evaluation index, the global expansion of network is carried out. After global expansion, the CNN is controlled to local expansion according to the recognition rate of cross validation samples. The local network learning is stopped until the recognition rate reaches the expected value. Finally, the training process for new samples, the adaptive incremental learning of network structure is realized by expanding some new branches. The superiority of proposed algorithm in network training time and recognition effect is verified through some image recognition experiments.
深度学习[1-2]是通过有监督或者无监督方式学习层次化特征表达,展现出高效而强大的特征学习和分类能力.常用深度学习模型包括自动编码器[3]、受限波尔兹曼机[4]、深度信念网络[5]、卷积神经网络(CNN, convolutional neural networks)[6]、生物启发式模型[7]等.
CNN是为识别二维图像而特殊设计的多层感知器. 1989年,LeCun等[8]采用误差梯度算法训练CNN,在手写数字识别中取得最好效果. 2012年,Krizhevsky等[9]使用并行化手段实现更深层次CNN. CNN在语音识别[10]及其表情识别[11]、情态意识识别[12]、光照变化人脸识别[13]、性别识别[14]、人脸检测[15]和人脸对齐[16]方面表现优异.另外,也有研究者针对CNN的模型结构及其参数问题开展相关研究,取得了一定研究成果[17-19].
鉴于CNN结构不可预知、过度依赖经验的缺点,并考虑到复杂多类问题中CNN模型构建策略的重要价值,笔者提出自适应深度CNN模型构建方法.首先,将初始CNN模型卷积层和池化层设置为仅含一幅特征图.然后,以CNN收敛速度为评价指标,对网络全局扩展,当系统平均误差达到预设值时,全局扩展结束.采用交叉验证样本测试扩展所得网络识别率,若识别率未达期望值,则对网络展开局部扩展,直到交叉验证样本识别率达到预设值后停止局部学习.最后,在保持原训练结果基础上学习新知识,实现新追加样本网络结构增量学习.
1 自适应深度CNN构建方法CNN性能会随神经元数目增加而相应提高,但卷积运算复杂度较高,盲目增大网络规模,则会耗费大量训练时间.而网络层数增加所提升的性能相对于增加的计算开销不成比例,识别精度有时略微提升,有时下降.目前针对网络模型的理论分析和量化研究比较匮乏,根据具体数据量以及数据本身特点,设计网络深度,设定网络特征图数,优化网络层次结构,提升网络性能是需要关注的研究方向.
笔者主要针对网络结构中特征图数不确定、训练难度大等缺点,从训练数据本身特点出发,通过网络结构的全局和局部自适应扩展的有机结合,实现网络特征图个数自主调节,并随网络结构的扩展,逐步加深网络深度,形成数据驱动的深层CNN.
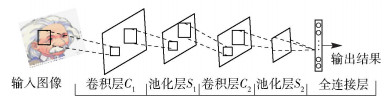
1.1 深度CNN结构初始化在网络初始化时,将网络深度设置为5层,且每层仅含一幅特征图,如图 1所示.初始模型只有一条支路,含2个卷积层(C1、C2)、2个池化层(S1、S2)和1个全连接层,每层仅含一幅特征图.
|
图 1 初始网络结构 |
训练过程中,采用反向传播(BP, backpropagation)算法更新权值,并通过收敛速度的大小判断当前网络是否达到最优.收敛速度定义为
| $ {{E}_{\text{hop}}}-{{E}_{\text{cun}}}\ge T $ | (1) |
其中:Ehop为初始系统期望平均误差;Ecun为当前系统真实平均误差;T为收敛速度的期望阈值,设定为0.1.
当前系统平均误差计算公式为
| $ {{E}_{\rm{cun}}}={{\left\| \mathit{\boldsymbol{Y}}-{{\mathit{\boldsymbol{Y}}}_{\rm{lab}}} \right\|}^{2}}=\frac{\sum\limits_{j=1}^{N}{\sum\limits_{i=1}^{m}{{{\left( y_{i}^{j}-y_{\rm{lab}}^{j} \right)}^{2}}}}}{N} $ | (2) |
其中:N为训练样本总数,m为类别数,yij为第j幅训练样本对应的第i个神经元的输出,ylabj为训练样本的真实类别标签,Y和Ylab为m×N的0、1二值矩阵.
按收敛速度的定义,若式(1) 成立,则表明初始网络具有训练至系统平均误差达到期望平均误差值的可能,而暂时不需要添加新的支路和特征图,一直训练该网络,直到系统平均误差达到期望值,此时网络为最优.如果训练过程中,式(1) 不成立,则认为该初始网络结构不能达到收敛,需对当前网络结构展开全局自适应扩展.
1.2 深度CNN结构全局扩展当网络需要全局扩展时,则在初始网络基础上全局扩展一条新支路B,如图 2所示.

|
图 2 全局扩展网络 |
在扩展新支路前,先保留已训练的初始网络A的卷积层和池化层相关参数及输出层输出结果yA.添加新支路B具有与A相似的结构,且在网络输出层产生新输出yB.在扩展的结构中,应当添加一个新的全连接层,将支路A和支路B输出融合到一起,并获得新输出结果.此时网络深度扩展为6层,含2个卷积层、2个池化层和2个全连接层.其中,输出层激励函数输出结果为
| $ \mathit{\boldsymbol{y = }}\mathit{f}\left( {{\mathit{\boldsymbol{y}}_{\rm{A}}} + {\mathit{\boldsymbol{\omega }}_{\rm{B}}}{\mathit{\boldsymbol{y}}_{\rm{B}}}} \right) $ | (3) |
其中:yA和yB为m×1二值向量;ωB为m维列向量,表示B支路输出权值,A支路输出权值设为1.
训练过程中A支路网络结构和相关参数固定不变,采用1.1节相似的方法,通过BP算法只更新B支路的相应权值,直到整个网络的系统平均误差达到期望值,则完成了网络全局扩展学习.
1.3 深度CNN结构局部扩展全局扩展后,网络系统平均误差低于期望值,但网络可能并未达到最优识别性能.因此,采用交叉验证样本对网络性能进行评估.当交叉验证样本识别率趋于某一稳定值,且此值一般为非理想状态时,网络全局扩展已不能改善识别率.此时需对全局扩展支路进行融合,构建形成新局部支路,从而实现网络结构局部扩展,提高CNN识别精度.
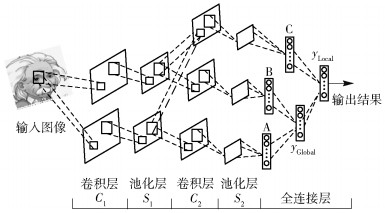
图 3展示了局部扩展后的网络结构,在执行局部扩展前,需保存已完成全局扩展模型的相关权重参数以及网络输出层的yGlobal值.在训练局部支路时,将全局扩展模型中池化层S1的特征图作为输入,进行特征融合,融合公式为
| $ {{C}_{2\text{Local}}}=f\left( {{S}_{1\text{A}}}*{{k}_{\text{A}}}+{{S}_{1\text{B}}}*{{k}_{\text{B}}} \right) $ | (4) |
|
图 3 全局和局部扩展后的网络结构 |
其中:C2Local为局部支路C2层的特征图,S1A、S1B分别为全局支路A、B在S1层的特征图,kA、kB为卷积核.融合方法采用简单的求和运算.
然后,将全局yGlobal值叠加到局部支路的输出层上,最后通过激励函数f(°)输出:
| $ \mathit{\boldsymbol{y = }}\mathit{f}\left( {{\mathit{\boldsymbol{y}}_{{\rm{Global}}}} + {\mathit{\boldsymbol{\omega }}_{{\rm{Local}}}}{\mathit{\boldsymbol{y}}_{{\rm{Local}}}}} \right) $ | (5) |
经过局部扩展,网络中添加一个新的全连接层,将全局扩展和局部扩展输出融合到一起,得到最终输出结果.此时网络深度已扩展为7层,含2个卷积层、2个池化层和3个全连接层.
训练过程中,全局各支路结构固定,在BP算法中只更新局部支路权值,直到交叉验证样本识别率达到期望值后停止学习,此时网络达到最高识别精确度.通过网络收敛速度控制网络全局扩展,采用交叉验证样本识别率判断是否需要执行局部扩展,深度CNN网络深度和每层特征图个数实现了自适应调整,且网络训练也由网络全部参数同时训练转化为参数分批训练,降低了训练难度和复杂度.
1.4 深度CNN结构的增量学习为丰富训练样本集,将新训练样本或被正确分类的测试样本加入训练样本集,以求能获得更优网络性能.传统基于特征学习的识别算法,因计算开销不大,可重新训练分类器.但深度CNN网络训练过程复杂,重新训练网络参数的计算开销太大,且当新增训练样本与原训练样本集差异较大时,网络学会了新知识,但丢失了原有学习记忆.而新增训练样本学习是典型增量学习问题,因此借助增量学习思想,提出深度CNN增量学习策略,该方法在对新增样本的训练中充分保留和利用历史训练结果,显著减少了后续训练时间.
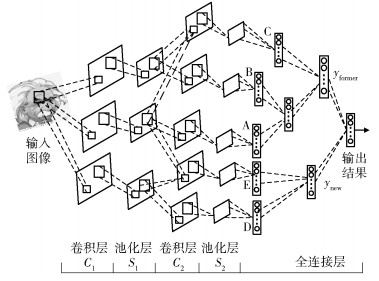
图 4所示为加入增量学习支路后的网络结构.保持原网络结构不变,当新增训练样本时,扩展全局支路D.基于BP算法,利用新增样本实现支路D的训练学习.若针对新增样本还需实现局部自适应扩展,则可将原网络中的S1A或S1B与S1D进行融合构建局部支路E,最终交叉验证识别率达到要求,则训练完成.此时网络深度已扩展为8层,网络总输出可表示为
| $ \mathit{\boldsymbol{y = }}\mathit{f}\left( {{\mathit{\boldsymbol{y}}_{{\rm{former}}}} + {\mathit{\boldsymbol{\omega }}_{{\rm{new}}}}{\mathit{\boldsymbol{y}}_{{\rm{new}}}}} \right) $ | (6) |
|
图 4 增量学习网络结构 |
采用CMU-PIE人脸库和MIT-CBCL人脸库进行实验验证. CMU-PIE人脸库含68位志愿者41 368张多姿态、光照和表情的面部图像.实验中,随机每人选取140幅灰度人脸,共9 520幅图像(含姿态、光照变化)作为训练样本集;每人选取5幅,共340幅图像作为交叉验证样本;每人选取5幅,共340幅图像做增量学习实验.然后,随机选取每人20幅人脸,共1 360幅图像作为测试样本. MIT-CBCL人脸库共10人,每人200幅图像,含姿态变化、微弱光照和表情变化.实验中,每人选取100幅人脸,共1 000幅图像作为训练样本.其中,每人选取10幅人脸,共100幅图像作为交叉验证样本;每人选取10幅人脸,共100幅图像做增量学习实验;其余800幅人脸作为测试数据.人脸图像尺寸均归一化为28×28.
2.2 传统CNN图像识别传统CNN采用2个卷积层、2个池化层和1个全连接层的5层结构.传统CNN结构为6-6-16-16,则卷积层C1和池化层S1分别含6幅特征图,卷积层C2和池化层S2分别含16幅特征图.激励函数一般采用Sigmoid函数,学习率设为0. 3,池化运算采用平均池化,卷积核大小为5×5或3×3.基于上述参数,进行了CNN图像识别实验,结果如表 1所示.
|
|
表 1 基于传统CNN不同结构情况的图像识别实验 |
实验结果表明,CNN中卷积层和池化层特征图数对训练时间和识别效果具有严重影响.不同人脸数据,达到最优识别效果的网络结构和参数配置完全不同.因此,基于经验或先验知识构建的网络结构不能充分反映样本数据本质特点,网络结构不具备普适性,且需消耗较多时间.
2.3 自适应深度CNN图像识别卷积层权重初始化中,假设输入特征图个数为n,输出特征图个数为m,卷积核大小为5×5,则卷积运算中需要初始化一个(n×52)×(m×52)维的权重矩阵,权重值采用均值为0,方差为
初始网络结构设置为1-1-1-1结构,如图 1所示.通过卷积核大小调整和结构自适应学习,可获得最佳网络.因输入图像像素归一化为28×28,全局扩展中卷积层C1的卷积核仅能设置为5×5,卷积层C2的卷积核可设置为5×5或3×3.局部扩展中卷积层的卷积核可选为5×5或3×3.实验结果如表 2和表 3所示.
|
|
表 2 深度CNN结构全局扩展中不同卷积核组合的实验结果 |
|
|
表 3 全局与局部扩展结合情况下不同卷积核组合的实验结果 |
表 2数据表明,不同大小卷积核对训练时间和识别率产生不同影响.因卷积核大小影响到连接权重个数,所以卷积核5-3(卷积层C1核为5×5,卷积层C2核为3×3) 组合训练时间比5-5组合训练时间明显降低.另外,识别性能受到一定影响,尽管卷积核5-3组合权重个数较少,但识别性能优于5-5组合.因此,网络中并不是权重数量越多越好,而每层特征图个数也不是越多越好.合理调整卷积核大小,根据数据样本自身情况,按需添加神经元,实现网络自适应扩展有利于提高运算效率,改善识别性能.
表 3结果表明,全局扩展卷积核5-3组合,局部扩展卷积核3×3时,网络训练时间最短,误分类率最低,因此选此组合为深度CNN构建过程中卷积核.两个人脸数据库上的样本训练得到的最优网络结构均为1-1-2-2结构.
与传统CNN实验对比表明,传统CNN在CMU-PIE和MIT-CBCL中获得的最优识别率分别为94.7%和96.875%,自适应深度CNN中,通过全局和局部扩展后获得的最优识别率分别为94.48%和95.50%.从网络构建时间看,传统CNN获取最优网络需耗费较多时间,通过大量重复实验确定;而自适应深度CNN尽管识别率没有达到传统CNN的最优值,但训练时间大大降低.
学习率α影响BP算法权值变化量,较大学习率可加快训练速度,但易导致系统不稳定;较小学习率则导致训练时间较长,网络收敛速度变慢,但能保证网络误差趋于最小值.网络设计中倾向选取较小的学习速率以保证系统稳定,一般范围在0.01~1之间.不同学习率下网络性能对比分析结果如表 4所示.
|
|
表 4 学习率对网络性能的影响实验 |
实验数据表明,最优学习率取值为0.6,此时网络训练时间和识别性能都比较好.研究发现,将初始学习率设置为较大值,然后随着训练过程进行,逐渐衰减学习率是有必要的,既可加快训练速度,又可使网络误差达到最小.因此进行了学习率衰减实验,初始学习率设置为0.9,网络训练中逐渐衰减学习率,每经过3个训练周期,将学习率衰减掉0.1,直到完成所有训练周期或达到最小学习率为止.实验表明,采用变学习率训练网络,CMU-PIE和MIT-CBCL人脸库训练时间分别下降10 s和2.5 s,但识别性能未降低.该方法有效缩减了通过实验获取最优学习率的时间,提高了网络训练效率.
2.4 自适应深度CNN的增量学习实验以全局和局部扩展的深度CNN最优网络为基础,对新增训练样本进行训练,增量学习新支路全局扩展中采用5-3组合卷积核,局部扩展为3×3,实验对比结果如表 5所示.
|
|
表 5 深度CNN增量学习后的实验结果 |
实验结果表明,增量学习后保留已学习好的网络结构,在新添支路时CMU-PIE和MIT-CBCL人脸库分别增加了28.55 s和9.67 s训练时间,大大减少新增样本训练学习的时间开销,且识别性能得到一定程度改善.增量学习中,深度CNN整体结构得到自适应调整,形成2-2-3-3结构模式,网络整体识别效果有较大改善.
3 结束语针对传统CNN在网络构建过程中过分依赖经验、训练难度大等不足,提出自适应深度CNN构建策略,并将该方法成功应用于图像识别.该算法根据网络需要添加神经元,实现了网络结构可控和可调,且算法学习训练过程有针对性,降低了训练难度.网络训练充分考虑数据自身特点,在保留前期训练结果基础上,对新增训练样本进行增量学习,减少重复训练的时间开销.实验结果证明了所提网络构建方法的有效性.未来研究中,将在更大规模图像识别中验证所提方法可行性,并对网络结构全局和局部自适应扩展的控制条件进行优化.
| [1] | Hinton G, Salakhutdinov R. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 5786(313): 504–507. |
| [2] | Arel I, Rose D C, Karnowski T P. Deep machine learning:a new frontier in artificial intelligence research[J]. IEEE Computational Intelligence Magazine, 2010, 5(4): 13–18. doi: 10.1109/MCI.2010.938364 |
| [3] | He YunLong, Kavukcuoglu K, Wang Yun, et al. Unsupervised feature learning by deep sparse coding[C]//2014 SIAM International Conference on Data Mining, Philadelphia, SIAM. 2014:902-910. |
| [4] | Kim L W, Asaad S, Linsker R. A fully pipelined FPGA architecture of a factored restricted boltzmann machine artificial neural network[J]. ACM Transactions on Reconfigurable Technology and Systems, 2014, 7(1): 1–23. |
| [5] | Hinton G, Osindero S, Teh Y. A fast learning algorithm for deep belief nets[J]. Neural Computation, 2006, 18(7): 1527–1554. doi: 10.1162/neco.2006.18.7.1527 |
| [6] | Pinheiro P, Collobert R. Recurrent convolutional neural networks for scene labeling[C]//Proceedings of The 31st International Conference on Machine Learning. Beijing:International Machine Learning Society, 2014:151-159. |
| [7] | Huang Yongzhen, Huang Kaiqi, Tao Dacheng, et al. Enhanced biologically inspired model for object recognition[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B:Cybernetics, 2011, 41(6): 1668–1680. doi: 10.1109/TSMCB.2011.2158418 |
| [8] | LeCun Y, Boser B, Denker J S, et al. Back propagation applied to hand written zip code recognition[J]. Neural Computation, 1989, 1(4): 541–551. doi: 10.1162/neco.1989.1.4.541 |
| [9] | Krizhevsky A, Sutskever I, Hinton G. ImageNet classification with deep convolutional neural networks[C]//Proceedings of the Advances in Neural Information Processing Systems. New York, NY, ACM, 2012:1097-1105. |
| [10] | Abdel-Hamid O, Mohamed A R, Jiang Hui, et al. Convolutional neural networks for speech recognition[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2014, 22(10): 1533–1545. doi: 10.1109/TASLP.2014.2339736 |
| [11] | Hamester D, Barros P, Wermter S. Face Expression recognition with a 2-channel convolutional neural network[C]//2015 International Joint Conference on Neural Networks. Piscataway, NJ:IEEE, 2015:1-8. |
| [12] | Xiong Chao, Zhao Xiaowei, Tang Danhang, et al. Conditional convolutional neural network for modality-aware face recognition[C]//2015 IEEE International Conference on Computer Vision. Piscataway, NJ:IEEE, 2015:3667-3675. |
| [13] | Pattabhi Ramaiah N, Ijjina E P, Mohan C K. Illumination invariant face recognition using convolutional neural network[C]//2015 IEEE International Conference on Signal Processing, Informatics, Communication and Energy Systems. Piscataway, NJ:IEEE, 2015:1-4. |
| [14] | Wolfshaar J V D, Karaaba M F, Wiering M A. Deep convolutional neural networks and support vector machines for gender recognition[C]//2015 IEEE Symposium Series on Computational Intelligence. Piscataway, NJ:IEEE, 2015:188-195. |
| [15] | Li Haoxiang, Lin Zhe, Shen Xiaohui, et al. A Convolutional neural network cascade for face detection[C]//2015 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway, NJ:IEEE, 2015:5325-5334. |
| [16] | Zhang Shaohua, Yang Hua, Yin Zhouping. Multiple deep convolutional neural networks averaging for face alignment[J]. Journal of Electronic Imaging, 2015, 24(3): 1–13. |
| [17] | Yun Dong, Yue Wu. Adaptive cascade deep convolutional neural networks for face alignment[J]. Computer Standards & Interfaces, 2015(42): 105–112. |
| [18] | Zhang Yuanyuan, Zhao Dong, Sun Jiande, et al. Adaptive convolutional neural network and its application in face recognition[J]. Neural Processing Letters, 2016, 43(2): 389–399. doi: 10.1007/s11063-015-9420-y |
| [19] |
连自锋, 景晓军, 孙松林, 等. 一种多尺度嵌套卷积神经网络模型[J]. 北京邮电大学学报, 2016, 39(5): 1–5.
Lian Zifeng, Jing Xiaojun, Sun Songlin, et al. Multi-Scale convolutional neural network model with multilayer maxout networks[J]. Journal of Beijing University of Posts and Telecommunications, 2016, 39(5): 1–5. |


