2. 华北电力大学 电气与电子工程学院, 北京 102206
提出了一种基于几何的适用于宽带多输入多输出(MIMO)移动端到移动端无线信道的随机散射模型.假设有效散射体位于三维(3D)双柱体的表面,将已有的窄带模型扩展到宽带并且把载频和带宽引入模型中,利用仿真实现信道,通过实现的信道矩阵进一步开展信道特征和参数研究,与现有的解析方法相比更加简单直接.通过对3D双柱体和二维双环散射模型的比较发现,3D模型对应的功率延迟分布的归一化功率和均方根时延扩展比二维的小,3D信道容量有一定的提升.
2. School of Electrical and Electronic Engineering, North China Electric Power University, Beijing 102206, China
A geometry-based stochastic scattering model for wideband multi-input multi-output (MIMO) mobile-to-mobile channels based on three dimensional (3D) two-cylinders was proposed. The proposed narrowband model is extended to wideband, and the carrier frequency and bandwidth was introduced into the model. The channel realization by using channel matrix is much more straight-forward and concise to study the channel characteristics compared with the too complicated analytical solutions available so far. The channel properties and parameters were further investigated based on the simulation model and realized channels. Simulations are compared with the two dimensional two-ring model. It can be found that the normalized power of power-delay-profile and root mean square delay spread of the proposed 3D model are smaller but the channel capacity are larger.
在移动自组织网络、智能传输系统和基于中继的蜂窝网中,移动端到移动端(M2M, mobile-to-mobile)通信起着重要作用.在M2M通信中,收发端天线等高且在相同环境中运动.在蜂窝网通信系统中,基站固定且远高于周围的环境,只有终端在移动.现有模型大多是针对这种固定端到移动端通信系统的,不能直接应用到M2M通信中.多输入多输出(MIMO, multi-input multi-output)系统使用多个天线收发器提升了空间和多路复用增益,可以有效地提高频谱效率和数据传输速率.因此,笔者对M2M MIMO信道模型展开研究.
对于M2M通信环境,Akki等[1]首次提出了二维(2D, two dimensional)参考模型用于单输入单输出M2M瑞利衰落信道,并且Akki[2]提出了相应的仿真模型. Pätzold和Hogstad等[3-4]提出了适用于窄带MIMO信道的基于双环的参考和仿真模型,但是只考虑了二次散射分量. Zajić等[5]针对窄带MIMO M2M莱斯衰落信道,提出了一个同时考虑一次和二次散射分量的更普遍的双环散射模型. Cheng等[6-7]针对窄带MIMO M2M信道,提出了一个更通用、自适应性更强的基于双环和椭圆几何形状结合的随机散射模型.在文献[6]中车辆交通密度首次在基于几何的窄带模型中引入. Cheng等[8]提出了一个基于双环和多个共焦椭圆的随机散射模型,这是第一次将车辆交通密度应用在宽带MIMO M2M信道的物理层设计.针对三维(3D, three dimensional)几何随机散射模型,Yuan等[9-10]提出了针对窄带和宽带MIMO M2M信道的双球和椭圆柱体结合的模型. Zajić[11]和Zajić等[12]分别提出了针对窄带和宽带MIMO M2M信道的双柱体模型.
在以上提到的基于几何的随机散射模型中,大部分是关于M2M窄带信道模型,它们的时空相关函数和多普勒功率谱等通过推导解析表达式进行分析,得到的解析表达式过于复杂且推导过程异常繁琐,尤其是基于多个几何形状的协同中继模型[13],而且通过解析式也只能得到非常有限的信道参数.其中Cheng等[8]、Yuan等[10]和Zajić等[12]提出了M2M宽带信道的概念,在时域窄带信号幅度计算基础上引入宽带信号幅度计算公式,但最终仍然推导和分析了M2M窄带信道参数和特性(原因可能是宽带信道解析解难于得到).而笔者把窄带模型扩展到宽带,宽带信号幅度与多径时延、载波频率和带宽相联系,通过仿真实现宽带信道冲激响应(CIR, channel impulse response)矩阵后,对表征信道宽带特性的重要模型和参数,如功率延迟分布(PDP, power-delay-profile)、均方根时延扩展(RMS-DS, root mean square delay spread)等进行了分析,信道实现方法简单,避免了推导复杂的信道参数和函数的解析表达式.
笔者基于3D双柱体和2D双环随机散射模型,对视距(LOS, line-of-sight)和非视距(NLOS, non-line-of-sight)场景信道的特征参数进行仿真比较研究.
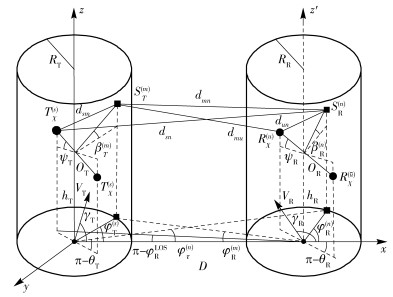
1 宽带MIMO M2M信道参考模型笔者提出了一个配备有LT个发射和LR个接收全向天线的宽带MIMO M2M模型,收发端天线均置于相同环境中,等高且都处在运动中,如图 1所示.假设有M个有效散射体位于发射端半径为RT的圆柱体表面,并且第m个有效散射体表示为ST(m),m∈{1, 2, …, M}.假设有N个有效散射体位于接收端半径为RR的圆柱体表面,且第n个有效散射体表示为SR(n),n∈{1, 2, …, N}. TX(s)是第s个发射天线,s∈{1, 2, …, LT}. RX(u)是第u个接收天线,u∈{1, 2, …, LR}. OT和OR分别是发射端和接收端天线阵列的中心点,这2个中心点之间的距离是D. dT和dR分别是位于发射端和接收端2个相邻天线之间的距离,并且假设max{dT, dR}≪min{RT, RR},max{RT, RR}≪D. θT和θR分别是发射端和接收端天线阵列位于x-y平面内的水平方位角. ψT和ψR分别是发射端和接收端天线阵列相对于x-y平面的垂直方位角.在运动角度γT和γR确定的方向下,发射端和接收端分别以速度VT和VR运动.
|
图 1 3D MIMO M2M双柱体几何散射模型 |
在图 1中,LOS分量直接从发射端传输到接收端,φTLOS和φRLOS分别是LOS分量的发射角和接收角.一次散射传输(SBT, single-bounce transmit)分量从发射端传输到接收端过程中只在发射端附近散射体ST(m)经过一次散射,水平发射角(AAoD, azimuth angle of departure)和垂直发射角(EAoD, elevation angle of departure)分别为φT(m)和βT(m),水平接收角(AAoA, azimuth angle of arrival)和垂直接收角(EAoA, elevation angle of arrival)分别为φR(m)和βR(m).一次散射接收(SBR, single-bounce receive)分量从发射端传输到接收端过程中只在接收端附近散射体SR(n)经过一次散射,AAoD和EAoD分别为φT(n)和βT(n),AAoA和EAoA分别为φR(n)和βR(n).二次散射(DB, double-bounce)分量在发射端传输到接收端过程中在发射端附近散射体ST(m)和接收端附近散射体SR(n)经过两次散射,AAoD和EAoD分别为φT(m)和βT(m),AAoA和EAoA分别为φR(n)和βR(n).
dsu、dsm、dmn、dun、dsn、dmu分别是TX(s)和RX(u)、TX(s)和ST(m)、ST(m)和SR(n)、RX(u)和SR(n)、TX(s)和SR(n)、ST(m)和RX(u)之间的距离.多径分量的传播时延可以通过这些几何距离计算得到.对于LOS场景,LOS分量的传播时延计算公式为
| $ \tau _{s,u}^{{\rm{LOS}}} = {d_{s,u}}/{c_0} $ | (1) |
其中c0为光在空气中的传播速度.
多径分量从发射端出发分别只经过散射体ST(m)、SR(n)到达接收端,经历的传输时间分别定义为SBT传播时延τs, um和SBR传播时延τs, un,计算公式分别为
| $ \tau _{s,u}^m = \left( {{d_{sm}} + {d_{mu}}} \right)/{c_0} $ | (2) |
| $ \tau _{s,u}^n = \left( {{d_{sn}} + {d_{un}}} \right)/{c_0} $ | (3) |
多径分量从发射端出发同时经过散射体ST(m)和SR(n)到达接收端所经历的传输时间定义为DB传播时延τs, umn,计算公式为
| $ \tau _{s,u}^{mn} = \left( {{d_{sm}} + {d_{mn}} + {d_{un}}} \right)/{c_0} $ | (4) |
LOS和NLOS场景的附加时延分别由传播时延减去最小传播延迟并进行升序排列得到,即
| $ \begin{array}{*{20}{c}} {{\tau _{{\rm{LOS}}}} = {\rm{sort}}\left\{ {\left[ {\tau _{s,u}^{{\rm{LOS}}},\tau _{s,u}^m,\tau _{s,u}^n,\tau _{s,u}^{mn}} \right] - } \right.}\\ {\left. {\min \left( {\tau _{s,u}^{{\rm{LOS}}},\tau _{s,u}^m,\tau _{s,u}^n,\tau _{s,u}^{mn}} \right)} \right\}} \end{array} $ | (5) |
| $ {\tau _{{\rm{NLOS}}}} = {\rm{sort}}\left\{ {\left[ {\tau _{s,u}^m,\tau _{s,u}^n,\tau _{s,u}^{mn}} \right] - \min \left( {\tau _{s,u}^m,\tau _{s,u}^n,\tau _{s,u}^{mn}} \right)} \right\} $ | (6) |
对于一个有LT×LR天线单元的MIMO系统,TX(s)-RX(u)链路的频率选择性复信道增益可以表示为LOS、SBT、SBR和DB分量的叠加.
LOS分量的复增益husLOS(t, τ)为
| $ \begin{array}{*{20}{c}} {h_{us}^{{\rm{LOS}}}\left( {t,\tau } \right) = }\\ {\sqrt {\frac{{{K_f}}}{{{K_f} + 1}}} \exp \left( {{\rm{j}}2{\rm{ \mathsf{ π} }}f_{us}^{{\rm{LOS}}}t - {\rm{j}}\frac{{2{\rm{ \mathsf{ π} }}}}{\lambda }{d_{su}}} \right)\delta \left( {\tau - \tau _{us}^{{\rm{LOS}}}} \right)} \end{array} $ | (7) |
SBT分量的复增益husSBT(t, τ)为
| $ \begin{array}{*{20}{c}} {h_{us}^{{\rm{SBT}}}\left( {t,\tau } \right) = \sqrt {\frac{{{\eta ^{{\rm{SBT}}}}}}{{{K_f} + 1}}} \mathop {\lim }\limits_{M \to \infty } \frac{1}{{\sqrt M }} \times \sum\limits_{m = 1}^M {\left\{ {\exp \left( {{\rm{j}}2{\rm{ \mathsf{ π} }}f_{us}^mt - } \right.} \right.} }\\ {\left. {\left. {{\rm{j}}\frac{{2{\rm{ \mathsf{ π} }}}}{\lambda }\left( {{d_{sm}} + {d_{mu}}} \right) + {\rm{j}}{\theta ^m}} \right)\delta \left( {\tau - \tau _{us}^m} \right)} \right\}} \end{array} $ | (8) |
SBR分量的复增益husSBR(t, τ)可以通过将式(8) 中的ηSBT→ηSBR, m→n, M→N替换得到.
DB分量的复增益husDB(t, τ)为
| $ \begin{array}{*{20}{c}} {h_{us}^{{\rm{DB}}}\left( {t,\tau } \right) = \sqrt {\frac{{{\eta ^{{\rm{DB}}}}}}{{{K_f} + 1}}} \mathop {\min }\limits_{\begin{array}{*{20}{c}} {M \to \infty }\\ {N \to \infty } \end{array}} \frac{1}{{\sqrt {MN} }} \times }\\ {\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {\left\{ {\exp \left( {{\rm{j}}2{\rm{ \mathsf{ π} }}f_{us}^{mn}t - {\rm{j}}\frac{{2{\rm{ \mathsf{ π} }}}}{\lambda }\left( {{d_{sm}} + } \right.} \right.} \right.} } }\\ {\left. {\left. {\left. {{d_{mn}} + {d_{un}}} \right) + {\rm{j}}{\theta ^{mn}}} \right)\delta \left( {\tau - \tau _{us}^{mn}} \right)} \right\}} \end{array} $ | (9) |
式(7)~式(9) 是在时域窄带信号幅度计算基础上得到宽带信号幅度与时延相关的计算公式,其中多径分量的增益仍是窄带意义.为了将信道增益扩展为宽带必须考虑功率延迟分布中多径分量的幅度衰减规律,这样一个LT×LR的MIMO M2M宽带CIR在LOS场景可表示为
| $ \begin{array}{*{20}{c}} {{h_{us}}\left( {t,\tau } \right) = \sqrt {P\left( \tau \right)} \left\{ {h_{us}^{{\rm{LOS}}}\left( {t,\tau } \right) + h_{us}^{{\rm{SBT}}}\left( {t,\tau } \right) + } \right.}\\ {\left. {h_{us}^{{\rm{SBR}}}\left( {t,\tau } \right) + h_{us}^{{\rm{DB}}}\left( {t,\tau } \right)} \right\}} \end{array} $ | (10) |
其中:P(τ)为多径功率延迟分布,其功率一般服从指数衰减[14],P(τ))=exp(-bτ),b为指数衰减因子.在NLOS场景LOS分量不存在且莱斯因子Kf=0,其他计算方法与LOS场景相同.
在式(7)~式(9) 中,λ为载波波长;Kf为莱斯因子;ηSBT、ηSBR和ηDB分别为SBT分量、SBR分量和DB分量对总的平均功率的贡献,且ηSBT+ηSBR+ηDB=1;θm、θn和θmn分别为有效散射体ST(m)、SR(n)、ST(m)和SR(n)引入的相位,这些相位均匀分布在区间[0, 2π)上;几何距离dsu、dsm、dmn、dun、dsn、dmu和由收发机运动产生的多普勒频移fusLOS、fusm、fusn、fusmn可以通过文献[12]计算得到.
DB分量的发射角与接收角相互独立.一次散射(SB,single-bounce)分量的发射角与接收角是相互关联的,它们之间的关系表达式可通过文献[12]得到.当2个圆柱体表面的散射体个数M和N趋近于无穷大时,假设AAoDφT(m)和AAoAφR(n)服从均匀分布,EAoDβT(m)和EAoAβR(n)的概率密度函数为
| $ f\left( \beta \right) = \left\{ \begin{array}{l} \frac{{\rm{ \mathsf{ π} }}}{{4\left| {{\beta _{\max }}} \right|}}\cos \left( {\frac{{\rm{ \mathsf{ π} }}}{2}\frac{\beta }{{{\beta _{\max }}}}} \right),\left| \beta \right| \le \left| {{\beta _{\max }}} \right| \le \frac{{\rm{ \mathsf{ π} }}}{2}\\ 0,\;\;\;\;其他 \end{array} \right. $ | (11) |
其中βmax为仰角的最大值,角度范围为0°≤|φm|≤20°.
2 宽带MIMO M2M信道仿真模型和信道实现第1节中描述的参考模型是一个理论模型,在理论模型中假设双柱体表面的散射体个数趋于无穷大,信道是无法实现的.从式(7)~式(9) 描述的参考模型出发,信道的随机仿真模型可以通过下面2个步骤得到[15]:① 令发射端和接收端的散射体数量M和N取有限值,M=MAME,N=NANE,MA和ME、NA和NE假设为分别在发射端和接收端水平面和垂直面上的散射体个数;② 确定离散随机变量发射角和到达角的值.通过有限谐波函数叠加法可以得到在LOS场景的随机仿真模型为
| $ \begin{array}{*{20}{c}} {{{\hat h}_{us}}\left( {t,\tau } \right) = \sqrt {P\left( \tau \right)} \left\{ {h_{us}^{{\rm{LOS}}}\left( {t,\tau } \right) + \hat h_{us}^{{\rm{SBT}}}\left( {t,\tau } \right) + } \right.}\\ {\left. {\hat h_{us}^{{\rm{SBR}}}\left( {t,\tau } \right) + \hat h_{us}^{{\rm{DB}}}\left( {t,\tau } \right)} \right\}} \end{array} $ | (12) |
其中:
计算仿真模型确定离散变量的方法有很多种[15].由于AAoD和AAoA假设服从均匀分布,因此选择改进的精确多普勒扩展法来确定离散的AAoD和AAoA,计算方法分别为
| $ \varphi _{\rm{T}}^{\left( {{m_{\rm{A}}}} \right)} = \frac{{\rm{ \mathsf{ π} }}}{{{M_{\rm{A}}}}}\left( {{m_{\rm{A}}} - \frac{1}{2}} \right) + {\theta _{\rm{T}}}\;\;\;\;\left( {1 \le {m_{\rm{A}}} \le {M_{\rm{A}}}} \right) $ | (13) |
| $ \varphi _{\rm{R}}^{\left( {{n_{\rm{A}}}} \right)} = \frac{{{\rm{2 \mathsf{ π} }}}}{{{N_{\rm{A}}}}}\left( {{n_{\rm{A}}} - \frac{1}{2}} \right) + {\theta _{\rm{R}}}\;\;\;\;\left( {1 \le {n_{\rm{A}}} \le {N_{\rm{A}}}} \right) $ | (14) |
EAoD和EAoA利用式(11) 中的概率密度函数,可以生成:
| $ \beta _{\rm{T}}^{\left( {{m_{\rm{E}}}} \right)} = \frac{{2\beta _{\rm{T}}^{\max }}}{{\rm{ \mathsf{ π} }}}\arcsin \left( {\frac{{2{m_{\rm{E}}}}}{{{M_{\rm{E}}}}} - 1} \right)\left( {1 \le {m_{\rm{E}}} \le {M_{\rm{E}}}} \right) $ | (15) |
| $ \beta _{\rm{R}}^{\left( {{n_{\rm{E}}}} \right)} = \frac{{2\beta _{\rm{R}}^{\max }}}{{\rm{ \mathsf{ π} }}}\arcsin \left( {\left( {\frac{{2{n_{\rm{E}}}}}{{{N_{\rm{E}}}}} - 1} \right.} \right)\left( {1 \le {n_{\rm{E}}} \le {N_{\rm{E}}}} \right) $ | (16) |
其中βTmax和βRmax分别为发射端和接收端天线的最大垂直角.
为了方便研究宽带信道特性,首先构造CIR的3D矩阵
| $ {\mathit{\boldsymbol{H}}\left( {q,t,f} \right) = \sum\limits_{i = 1}^l {\hat h\left( {q,t,\tau } \right)\exp \left( { - {\rm{j}}2{\rm{ \mathsf{ π} }}{f_i}\tau } \right)} } $ | (17) |
| $ {h\left( {q,t,\tau } \right) = {F^{ - 1}}\left\{ {\mathit{\boldsymbol{H}}\left( {q,t,f} \right)} \right\}} $ | (18) |
其中:fi为采样频率,F-1{·}表征傅里叶逆变换.起始和最终频率分别为f1=fc-B/2和fI=fc+B/2,fc为载波频率,B为带宽,Δf为2个相邻频率采样点之间的频率间隔,则fi=f1+(i-1)Δf(i=1, 2, …, I),I为频率样本总数.
3 信道特征参数计算及分析基于3D双柱体模型的M2M MIMO宽带信道矩阵的实现,进一步研究了在LOS和NLOS场景下的多普勒功率谱密度(D-PSD,Doppler power spectral density)、PDP、RMS-DS和信道容量等信道特征量,并将仿真结果与2D双环模型[5]进行了对比,分析了2D和3D信道特征的异同.为满足广义平稳非相关散射条件,将不同路径上归一化的冲激响应划分到多个子窗口中,在信道模型和参数的计算过程中假设信道在20λ子窗内是宽平稳非相关的.
为了使所提出的宽带MIMO M2M信道与实际应用相符,首先假设在LOS和NLOS场景下接收信号电平门限都为-120 dBm,从而重新确定了由式(5) 和式(6) 得到的时延范围.同时,假设在LOS和NLOS场景下的功率动态范围分别为25 dB和20 dB[14],从而可以得到功率的指数衰减因子b.
在仿真中,3D宽带MIMO M2M双柱体几何模型的基本参数选择如下[12]:LT=LR=2,fc=5 GHz,B=100 MHz,Kf=5,dT=dR=λ,θT=θR=0°,ψT=ψR=0°,γT=γR=π/2,D=300 m,RT=RR=20 m,VT=VR=1 m/s.发射端和接收端2个圆柱体表面上的散射体个数分别为MA/ME=22/9,NA/NE=40/9. 2D双环模型的仿真参数与3D双柱体模型的水平面参数相同.
3.1 D-PSD两个复包络hus(t)和hu′s′(t)的归一化的空时相关函数(ST-CF, space-time correlation function)为
| $ {R_{us,u's'}}\left( {{d_{\rm{T}}},{d_{\rm{R}}},\Delta t} \right) = \frac{{E\left\{ {{h_{us}}\left( t \right)h_{u's'}^ * \left( {t - \Delta t} \right)} \right\}}}{{\sqrt {E\left\{ {{{\left| {{h_{us}}\left( t \right)} \right|}^2}} \right\}E\left\{ {{{\left| {{h_{u's'}}\left( t \right)} \right|}^2}} \right\}} }} $ | (19) |
其中:(·)*表示复共轭操作,E{·}表征统计期望算子.当u=u′,s=s′时,Rus, u′s′即为自相关函数.对自相关函数做傅里叶变换即可得到D-PSD.
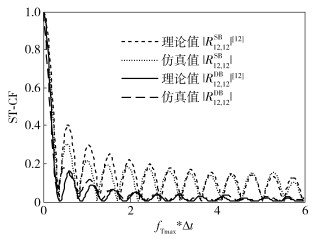
正如第1节提到的,大部分关于M2M的文献都是利用解析表达式推导得到信道的ST-CF.为了验证通过信道矩阵实现宽带信道的ST-CF与当前文献中通过解析式得到的ST-CF一致,分别将所得到的SB和DB分量的ST-CF与通过文献[12]中解析式(30)~式(32) 得到的SB和DB分量的ST-CF进行了对比,本文和文献[12]采用相同的仿真参数,结果如图 2所示.由图 2可以看出,本文的仿真结果与文献[12]的解析结果吻合,存在细微的差别是因为在利用解析表达式推导过程中假设有效散射体的个数趋于无穷大,但在本文仿真中散射体的个数是有限的.
|
图 2 本文仿真结果与文献[12]中解析结果[ST-CF(dT=dR=λ)]的比较 |
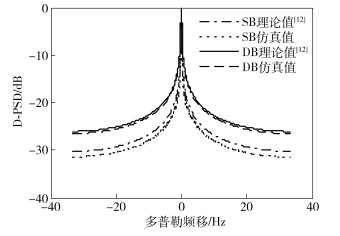
同时,通过宽带信道矩阵仿真得到的SB和DB分量的D-PSD与文献[12]中的宽带模型解析式(48)~式(50) 计算得到的理论结果进行了对比,如图 3所示.由图 3可以看出,本文仿真得到的D-PSD与文献[12]的理论结果吻合.
|
图 3 本文仿真得到的D-PSD与文献[12]中解析结果的比较 |
PDP可以通过CIR计算得到. 图 4为所提出的3D模型和2D双环模型的归一化平均PDP在LOS和NLOS场景下的对比.从图 4中可以看出,所有的PDP呈类指数衰减分布.不论是3D模型还是2D模型,在NLOS场景下的归一化功率要比LOS场景下的大;不论在LOS还是在NLOS场景下,大部分的2D模型的归一化功率要比3D的大.

|
图 4 3D模型与2D双环模型的归一化功率在LOS和NLOS场景下的比较 |
宽带多径信道的时间色散特性由RMS-DS来定量表示. RMS-DS是功率时延分布的二阶矩的平方根. 图 5为LOS和NLOS场景下所提出的3D模型和2D双环模型的RMS-DS的累积概率分布函数(CDF, cumulative distribution function)与理论拟合曲线的比较.从图 5中可以看出,宽带MIMO M2M无线信道的RMS-DS大致服从对数正态(lognormal)分布. 表 1给出了RMS-DS在CDF曲线给定概率为10%、50%、90%的值,以及平均值和标准差.可以看出,不论是2D还是3D模型,在NLOS场景的RMS-DS比LOS场景的要大.并且,不论是LOS还是NLOS场景,2D模型的RMS-DS比3D模型的要大.

|
图 5 3D模型与2D双环模型的RMS-DS在LOS和NLOS场景下的比较 |
|
|
表 1 RMS-DS统计值 |
图 6为在LOS和NLOS场景下,所提出的3D模型和2D双环模型信道容量的比较.从图 6中可以看出,不论在LOS还是在NLOS场景下,3D模型的信道容量都要比2D的大.当信噪比为20 dB时,3D NLOS的信道容量比2D NLOS的信道容量高0.4 bit·s-1·Hz-1,3D LOS的信道容量比2D LOS的信道容量高0.5 bit·s-1·Hz-1,这与文献[16]的结果一致. 3D和2D模型在NLOS场景下的信道容量比LOS场景的要大,因为NLOS的散射体环境比LOS丰富,信道之间的相关性会变小.从图 6中也可看到,信噪比的增加对信道容量的提升有着很大的影响.由于发射天线和接收天线具有空间相关性,3D和2D模型的信道容量都比瑞利独立同分布(Rayleigh i. i. d)信道的容量要小.为简化理论模型复杂性和减少仿真时间,主要是针对物联网中MIMO M2M信道容量进行比较研究,所以在移动终端天线数目都取2.随着终端天线数目的增加,期望3D比2D MIMO信道容量有更大的提升.

|
图 6 3D模型与2D双环模型的信道容量在LOS和NLOS场景下的比较 |
笔者提出了一个适用于宽带MIMO M2M无线信道的基于2个圆柱体的几何随机散射模型.创新点是将MIMO M2M信道模型从窄带扩展到宽带并引入了载波频率和带宽.此外,为了避免复杂的信道特征参数和函数的数学推导,首先利用所建立的宽带MIMO M2M信道仿真模型得到信道的冲激响应仿真矩阵,基于实现的信道仿真矩阵,在LOS和NLOS场景下对信道特征量分别进行了分析研究,并将3D双柱体模型的仿真结果与2D双环模型的仿真结果进行了对比.结果表明,不论在LOS还是在NLOS场景下,3D模型的PDP中的归一化功率要比2D的小,3D模型的信道容量都要比2D的大.对于3D和2D模型,在NLOS场景下PDP中的归一化功率和信道容量都要比LOS场景下的大. 2D NLOS、2D LOS、3D NLOS、3D LOS的RMS-DS依次减小.
| [1] | Akki A S, Haber F. A statistical model for mobile-to-mobile land communication channel[J]. IEEE Transactions on Vehicular Technology, 1986, 35(1): 2–10. doi: 10.1109/T-VT.1986.24062 |
| [2] | Akki A S. Statistical properties of mobile-to-mobile land communication channels[J]. IEEE Transactions on Vehicular Technology, 1994, 43(4): 826–831. doi: 10.1109/25.330143 |
| [3] | Pätzold M, Hogstad B O, Youssef N, et al. A MIMO mobile-to-mobile channel model:Part Ⅰ-The reference model[C]//IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC). Berlin, Germany:[s.n.], 2005:573-578. |
| [4] | Hogstad B O, Pätzold M, Youssef N, et al. A MIMO mobile-to-mobile channel model:Part Ⅱ-The simulation model[C]//IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC). Berlin, Germany:[s.n.], 2005:562-567. |
| [5] | Zajić A G, Stüber G L. Space-time correlated mobile-to-mobile channels:modeling and simulation[J]. IEEE Transactions on Vehicular Technology, 2008, 57(2): 715–726. doi: 10.1109/TVT.2007.905591 |
| [6] | Cheng Xiang, Wang Cheng-xiang, Laurenson D, et al. An adaptive geometry-based stochastic model for non-isotropic MIMO mobile-to-mobile channels[J]. IEEE Transactions on Wireless Communications, 2009, 8(9): 4824–4835. doi: 10.1109/TWC.2009.081560 |
| [7] | Cheng Xiang, Wang Cheng-xiang, Ai B, et al. Envelope level crossing rate and average fade duration of non-isotropic vehicle-to-vehicle ricean fading channels[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(1): 62–72. doi: 10.1109/TITS.2013.2274618 |
| [8] | Cheng Xiang, Yao Qi, Wen Miao-wen, et al. Wideband channel modeling and intercarrier interference cancellation for vehicle-to-vehicle communication systems[J]. IEEE Journal on Selected Areas in Communications, 2013, 31(9): 434–447. doi: 10.1109/JSAC.2013.SUP.0513039 |
| [9] | Yuan Yi, Cheng Xiang, Wang Cheng-xiang, et al. Novel 3D geometry-based stochastic models for non-isotropic MIMO vehicle-to-vehicle channels[J]. IEEE Transactions on Wireless Communications, 2014, 13(1): 298–308. doi: 10.1109/TWC.2013.120313.130434 |
| [10] | Yuan Yi, Cheng Xiang, Wang Cheng-xiang, et al. 3D wideband non-stationary geometry-based stochastic models for non-isotropic MIMO vehicle-to-vehicle channels[J]. IEEE Transactions on Wireless Communications, 2015, 14(12): 6883–6895. doi: 10.1109/TWC.2015.2461679 |
| [11] | Zajić A G. Impact of moving scatterers on vehicle-to-vehicle narrowband channel characteristics[J]. IEEE Transactions on Vehicular Technology, 2014, 63(7): 3094–3106. doi: 10.1109/TVT.2014.2299239 |
| [12] | Zajić A G, Stüber G L. Three-dimensional modeling and simulation of wideband MIMO mobile-to-mobile channels[J]. IEEE Wireless Communications, 2009, 8(3): 1260–1274. doi: 10.1109/TWC.2009.070379 |
| [13] | Talha B, Pätzold M. A Geometrical three-ring-based model for MIMO mobile-to-mobile fading channels in cooperative networks[J]. EURASIP Journal on Advances in Signal Processing, 2011(1): 1–13. |
| [14] | Zhao Xiongwen, Liang Xiaolin, Li Shu, et al. Two-Cylinder and multi-ring GBSSM for realizing and modeling of Vehicle-to-Vehicle wideband MIMO channels[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(10): 2787–2799. doi: 10.1109/TITS.2016.2526652 |
| [15] | 王雪利. MIMO M2M移动衰落信道残缺双环模型及其统计特性[D]. 武汉: 武汉理工大学, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10497-2010165824.htm |
| [16] | 王营. 3D MIMO信道建模研究[D]. 武汉: 武汉理工大学, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10614-1013331405.htm |


