采用两种不同的方法对同一新建电磁混响室的场均匀性进行了评定、对比和分析,一种是基于最大场强统计特性,具有优于相关国际标准的技术指标;另一种方法是基于不同搅拌状态下被测场强的概率分布,将任意搅拌状态下的被测场强均纳入场均匀性判定过程中.两种评定方法所得结果具有一致性和差异性,一致性证明了新方法能够从场强概率分布的角度对混响室的场均匀性进行有效验证;差异性则说明了新方法可以为射频识别芯片最大识别距离测试、复杂信道模拟等应用提供更为全面和准确的基础技术指标支撑.
The field uniformity of the same reverberation chamber is validated by the traditional method which is based on maximal field, and its results indicate that the technical specification of reverberation chamber is much better than that required in related international standard. A new method based on the probability distribution of field is introduced here. The field during the whole period of stirrers' rotating is taken into account. The general accordance from these two methods indicates that the new method is useful for the validation from another new point of view. The partial difference proves that the new method should be adopted for better specification supporting in some special applying, such as maximum reading distance measurement for radio frequency identification and simulation of complex wireless channel.
电磁混响室(RC,reverberation chamber)能够在其工作区内产生统计意义上各向同性的均匀电磁场[1],因此被国际电工委员会(IEC, international electrotechnical commission)确定为抗扰度测试的重要装置之一[2-3].同时,在场强相关测试的基础上,RC还应用于短距离无线通信系统的接收灵敏度测试[4]、复杂无线信道模拟复现[5]以及多输入多输出系统信道测试中[6]. RC建设完成后,需要对其场均匀性进行严格评定,以确保应用中场强相关量值的准确可靠.
1 实验装置与参数被测RC由中国计量科学院于2015年7月建设完成,内部腔体净尺寸为6.43 m(长)×5.09 m(宽)×5.75 m(高),理论最低可用频率约为100 MHz[2],测试区域尺寸约为2 m(长)×1 m(宽)×2 m(高),内设分别为水平和垂直放置的两组机械搅拌桨,其外形及机械搅拌桨设置如图 1所示.

|
图 1 RC外观 |
由于100 MHz定向发射天线的尺寸过大而不利于现场布放,所进行实验过程中采用的发射天线频率范围为200 MHz~4 GHz.
测试中采用的仪器设备及重点参数如表 1所示.
|
|
表 1 设备与参数 |
首先按照IEC 61000-4-21-2011[2]所推荐的评定方法对工作区域内的场均匀性进行评定,其关键测量流程如下:
1) 将发射天线置于固定位置和朝向.
2) 选定被测位置为工作区域的8个顶点位置中的一个,将三维场强探头放置在被测位置.
3) 连接信号源、功率放大器、发射天线、场强探头、场强读数器,如图 2所示.其中,信号源与发射天线通过铠装线缆连接,场强探头与场强读数器通过光纤连接.

|
图 2 实验装置图 |
4) 通过搅拌桨控制器将横、竖两组桨叶分别旋转15°后静止.
5) 控制信号源在被测频率点处发射具有相应频率的连续波,连续波功率调整为适当水平.
6) 记录稳定状态下该被测位置处X轴、Y轴、Z轴3个方向上不同频率处的场强大小.
7) 改变被测位置,其他设置保持不变,重复步骤1)~6) 完成其他7个位置的测量.
不同被测位置、不同方向、不同搅拌桨状态及不同频点处记录的场强可以表示为E(p, d, s, fn),其中p=1~8为被测位置的编号,d=1, 2, 3分别代表X、Y、Z轴3个方向,s=1~24为搅拌桨状态的编号,fn为被测频率.
则相应参数条件下该工作区域内的场均匀性可由式(1)~式(4) 得到.
| $ {{E}^{\max }}\left( p, d, {{f}_{n}} \right)=\max \left[E\left( p, d, s, {{f}_{n}} \right) \right] $ | (1) |
| $ \alpha \left( {{f}_{n}} \right)=\left\langle {{E}^{\max }}\left( p, d, {{f}_{n}} \right) \right\rangle $ | (2) |
| $ \sigma \left( {{f}_{n}} \right)=\text{std}\left[{{E}^{\max }}\left( p, d, {{f}_{n}} \right) \right] $ | (3) |
| $ {{\sigma }^{\text{dB}}}\left( {{f}_{n}} \right)=101\text{g}\left[\frac{\sigma \left( {{f}_{n}} \right)+\alpha \left( {{f}_{n}} \right)}{\alpha \left( {{f}_{n}} \right)} \right] $ | (4) |
其中:max[E(p, d, s, fn)]为对不同搅拌桨位置(s=1~24) 下测量得到的数据取最大值;〈Emax(p, d, fn)〉为对不同位置(p=1~8) 及不同方向(d=1, 2, 3) 的数据取平均值,std[Emax(p, d, fn)]为对不同位置及不同方向的数据取标准差,σdB(fn)为最终计算得到的以dB为单位的场均匀性指标.
需要说明的是,实际评定流程较为复杂,场强设置、被测位置选择、搅拌桨位置调整等方面的细节在此不予逐条描述,以便突出场均匀性评定的核心内容并与后续研究结果对比.
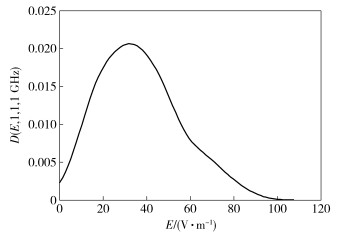
3 基于场强概率分布的评定以位置1处X轴方向工作频率为1 GHz时的场强为例,特定位置及特定方向上在不同搅拌桨状态下测得的场强概率分布函数如图 3所示,场强值分布在(0~120) V/m的范围内,其中场强值较小及较大时出现的概率都较小,呈现一定的峰值分布特征.对于不同搅拌桨状态下所测得的场强,IEC标准仅将其统计意义上的最大值作为场均匀性判断的依据[2],如式(4) 所示,即相当于只考查了图 3中右侧极限位置所代表的情况.可以看到,极大值在测量中出现的概率已经趋近于零,因此极易被搅拌桨位置的精确程度等外在因素干扰,具有一定的偶然性.
|
图 3 典型频率、位置及方向上的场强概率分布函数曲线 |
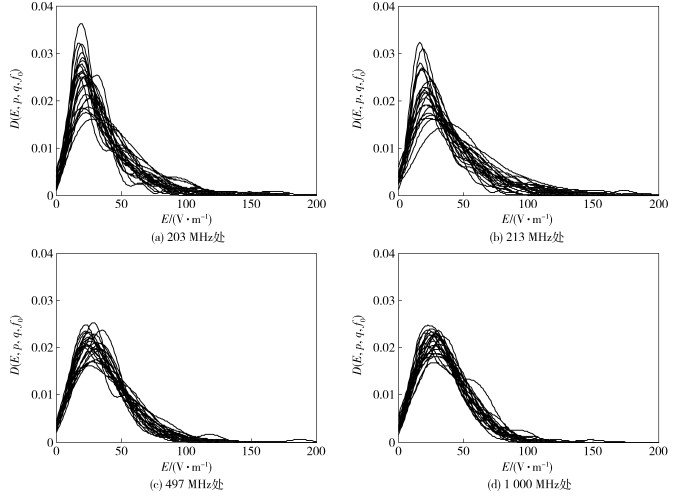
对比工作频率分别为203 MHz、213 MHz、497 MHz及1 GHz时不同位置及不同方向的场强概率分布状态(分别有24条曲线),如图 4所示,可以发现工作频率在1 GHz及497 MHz时的整体吻合程度好于在203 MHz及213 MHz的情况.因此从理论上说,且定性判断实验数据可以认为,场强概率分布的吻合程度也能够从侧面反映该频点处的场均匀性.相关学者对不同测试位置和不同搅拌状态下的场强概率分布进行了研究[7],但尚无应用于混响室场均匀性评定的报道.基于图 4的定性分析,提出定量判定场强概率分布的方法:
| $ \bar{D}\left( E, {{f}_{n}} \right)=\left\langle D\left( E, p, d, {{f}_{n}} \right) \right\rangle $ | (5) |
| $ {{D}_{\text{diff}}}\left( E, p, d, {{f}_{n}} \right)=\left| D\left( E, p, d, {{f}_{n}} \right)-\bar{D}\left( E, {{f}_{n}} \right) \right| $ | (6) |
| $ D_{\text{diff}}^{\text{sum}}\left( p, d, {{f}_{n}} \right)=\sum\limits_{E}{{{D}_{\text{diff}}}\left( E, p, d, {{f}_{n}} \right)} $ | (7) |
| $ \delta \left( {{f}_{n}} \right)=\left\langle D_{\text{diff}}^{\text{sum}}\left( p, d, {{f}_{n}} \right) \right\rangle $ | (8) |
|
图 4 典型频率处不同位置及不同方向的场强概率分布 |
其中:D(E, p, d, fn)为各位置、方向及工作频率下所测得的不同搅拌桨状态下的场强概率分布,D(E, fn)为8个不同位置及3个不同方向综合的平均概率分布,Ddiff(E, p, d, fn)为各位置、方向及工作频率下场强概率分布与平均概率分布D(E, fn)的绝对偏差,Ddiffsum(p, d, fn)为Ddiff(E, p, d, fn)的概率累计,δ(fn)为Ddiffsum(p, d, fn)的均值可以用于评定目标区域内的场均匀性.
δ(fn)表征了各位置和各方向上的场强概率分布偏离整个区域所有方向上平均的场强概率分布的距离程度.考虑极限情况:当δ(fn)=0时,表明不同位置及不同方向的场强概率分布均完全保持一致,场均匀性为绝对的均匀状态;当δ(fn)→1时,表明不同位置及不同方向的场强概率分布完全离散,场均匀性为绝对的混沌状态.因此,δ(fn)可以用于从场强概率分布的角度对RC场均匀性进行定量评定.
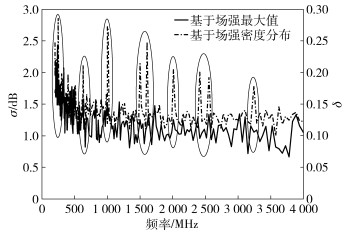
4 对比与讨论采用两种不同的方法对同一个目标RC的场均匀性评定结果如图 5所示.经典方法评定结果表明工作区场均匀性在200 MHz~1 GHz频率范围内均优于2.5 dB,在1 GHz~4 GHz频率范围内基本优于1.5 dB,满足并优于IEC标准的要求[2],表明该新建RC在场均匀性指标上具有较高水平.
|
图 5 场均匀性评定结果 |
对比两种评定方法所得结果,可以观察并分析得到以下两方面的重要特征.
1) 单个场强概率分布曲线的基本形状均保持一致,如图 3和图 4所示,因此场强最大值的均匀性与场强概率分布的均匀性会在整体趋势上保持一致,如图 5所示.既反映了被测RC在较高频率范围内的场均匀性优于较低频率范围内的场均匀性,符合理论预期[1-2],也间接验证了基于场强概率分布的评定方法对RC场均匀性的有效性.
2) 在局部范围内,如图 5中椭圆框所表示的部分,也会出现场强最大值的均匀性与场强概率分布均匀性相背离的局部状态.这是由场强概率分布曲线的局部特征并不保持恒定所造成的.如图 3所示,场强概率分布曲线的峰值、半高宽度并不保持恒定.因此,当搅拌桨转动全周期内产生的场强均对RC的应用产生影响时,有必要采用提出的新方法进行局部更为细致的评定.
总体来说,该一致性和差异性证明两种评定方法所得结果均有效评价了RC的场均匀性,但应具有不同的适用范围.
具体来说,两种评定方法的适用范围与其评定要素直接相关.对抗干扰度测试、接收灵敏度测试[3]等只与最大场强相关的测试来说,只有搅拌桨转动周期内的最大场强才对测试结果产生影响,适用于基于最大场强的评定方法.与场强的时变特征相关的应用中,包含最大场强在内的所有搅拌状态下的所有场强均对相关测试产生影响,此时基于场强概率分布的评定方法会具有更好的适用性.例如,对于与识别概率相关的射频识别最大读取距离测试来说[4],不同搅拌状态下的场强均对识别概率产生影响;与信道时变特征相关的复杂信道模拟中,场强的变化影响信道路径损耗、时延[8]等参量.在这些应用中,有必要将考虑场强的概率分布的均匀性作为RC场均匀性评定的补充方法,以更准确地反映RC的技术参数对测试结果的影响.
不同位置或不同搅拌状态下的场强概率分布已经在相关文献中得到了初步研究,但本研究首次给出了具体的量化评定方法,并将该方法实践于混响室场均匀性评定中.
5 结束语笔者对一新建RC的场均匀性进行了评定,得到了优于IEC标准的场均匀性指标,同时还在传统评定方法的基础上提出了基于场强概率分布的评定方法,相关实验结果证明了新方法的有效性.最后分析了两种评定方法的有效性,并且对两种方法在不用应用中的适用性进行了讨论.
| [1] | Corona P, Ladbury J, Latmiral G. Reverberation-chamber research-then and now:a review of early work and comparison with current understanding[J]. IEEE Transactions on Electromagnetic Compatibility, 2002, 44(1): 87–94. doi: 10.1109/15.990714 |
| [2] | Piette M, Tsigros C. IEC 61000-4-21 testing:selective source-mode tuning with two orthogonal antennas scanning system[C]//2008 International Symposium on Electromagnetic Compatibility-EMC Europe. Hamburg:IEEE, 2008:1-6. |
| [3] | IEC 61726-1999, Cable assemblies, cables, connectors and passive microwave components-screening attenuation measurement by the reverberation chamber method[S]. IEC, 1999. |
| [4] | Rudander J H, Ikram-e-Khuda, Kildal P S, et al. Measurements of RFID tag sensitivity in reverberation chamber[J]. IEEE Antennas & Wireless Propagation Letters, 2011(10): 1345–1348. |
| [5] | Guo Xiaotao, He Zhao, Zhang Yichi, et al. Theoretical uncertainty of RMS delay spread simulated by reverberation chamber[C]//International Conference on Electronic Measurement & Instruments (ICEMI). Qingdao:IEEE, 2015:426-430. |
| [6] | Lotback Patane C, Skarbratt A, Rehammar R, et al. On the use of reverberation chambers for assessment of MIMO OTA performance of wireless devices[C]//20137th European Conference on Antennas and Propagation (EuCAP). Chalmers:IEEE, 2013:101-105. |
| [7] | Kostas J G, Boverie B. Statistical model for a mode-stirred chamber[J]. IEEE Transactions on Electromagnetic Compatibility, 1991, 33(4): 366–370. doi: 10.1109/15.99120 |
| [8] | Delangre O, De Doncker P, Lienard M, et al. Delay spread and coherence bandwidth in reverberation chamber[J]. Electronics Letters, 2008, 44(5): 328–329. doi: 10.1049/el:20083676 |


