提出了一种动态规划算法解决手机拍照文档图像的边界检测问题.根据手机拍照文档图像的特点,设计新的动态规划模型,提出了利用逻辑回归二分类算解决文档区域4个边的组合问题.虽然手机拍照的文档图像一般比较模糊,光照不均匀,畸变,但是这些算法很好地解决了手机拍照文档图像的边界检测和组合问题.
The detection algorithm of the edge of the document area in the mobile image was presented. According to the characteristics of mobile image, a new dynamic programming model was designed. A combination of four edges of document area was proposed by using the two classification of logistic regression. Although the mobile images are generally blurred, uneven illuminated and distorted, these algorithms can solve the problem of boundary detection and combination of document area of mobile image well.
随着智能手机的普及和手机摄像功能越来越强大,一些传统数码相机和扫描仪功能逐渐被手机拍照功能代替.目前有很多应用程序通过手机拍照纸质文档,把文档区域从背景图像中分离出来,进行图像增强,可以达到扫描仪的效果.虽然手机拍照文档图像简单、方便和经济,但是由于手机拍照的文档图像中,携带与文档无关的背景,需要把文档区域从背景图像中分离出来.从背景图像中分割文档区域,属于图像分割技术.手机拍照图像的主要特点是:文档区域作为背景图像的目标在图像中所占比例较大,通常大于70%;纸质文档的物理边界是矩形,边界一般是直线.所以对文档区域的分割方法一般采用基于边缘的分割方法,比如通过霍夫变换检测直线[1-2]的方法确定文档区域的边缘,实现目标的分割. Zhang等[3]在白板扫描和图像增强的论文中用霍夫变换从背景图像中寻找白板的边界,抠出白板区域,实验结果也表明霍夫变换解决了白板图像的搜边问题,但是论文中使用的拍照设备是高分辨率的数码相机,并且相机是固定的,图像质量远高于手机拍照图像,白板边界复杂度却低于手机图像.相对而言,手机拍照具有以下特点:
1) 由于手机是移动手持设备,拍照过程中容易发生抖动,造成拍照图像不清晰,经常会模糊,如图 1(a)所示;

|
图 1 手机拍照产生的低质量图像 |
2) 通常拍照是在自然场景进行,光线不均匀,例如在晚上,依靠室内灯光照射拍照,造成图像光线不均匀,有阴影产生,如果打开手机自带闪光灯,文档图像会包含亮斑,如图 1(b)(c)所示;
3) 拍照的纸质文档,经常是书本的某一页,文档所在平面并非水平,拍照文本图像会发生几何畸变,如图 1(d)所示.
手机拍照产生的图像一般比较模糊,噪点多,加上文本内容本身有很多文字、图表、图形等.实验表明,图像经过霍夫变换产生的线段比较多,而且会产生大量的短线段,如图 2(a)所示;对于弯曲的边界,则会产生多条线段,如图 2(b)所示.另外,标准霍夫变换算法时间复杂度O(N3),即使经过优化,计算量仅可以降低到O(N2lb2N)[4],当图像比较大,算法时间会很长,无法满足用户的实时需求.实验证明,霍夫变换并不适应于手机拍照的图像的边界检测.

|
图 2 霍夫变换检测 |
为了解决手机拍照图像中文档区域边界检测问题,采用动态规划算法[5].动态规划算法是由Bellman等在研究多阶段决策过程(multistep decision process)的优化问题时提出的.
在计算机视觉领域,动态规划有很多应用场景,Amini[6]利用动态规划算法,通过建立主动轮廓模型实现目标物体的分割;Sonka等[7]利用动态规划检测直线;Merlet等[8]利用动态规划在遥感卫星图像中,检测道路方向;Ungru[9]用动态规划在医学图像实现目标分割;Rosado-Tora等[10]提出基于极坐标下的成本函数的动态规划算法,实现目标物体的自动分割.
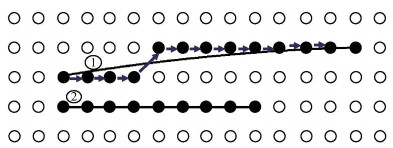
对于N行M列的图像,图像数字化后,文档的边界由离散的像素点组成,图像经过二值化处理后,像素点只有黑白2种状态,如图 3所示.假设文档的边界由黑色像素点组成,在手机拍照图像中,文档区域占整个图像的70%以上,如果一条路径是文档区域的上边界,这条路径一定是从左到右,接近水平,经过前景点最多的路径.如图 3所示,图中标出的路径1,虽然不在一条直线上,但是相比于图中路径2,更有可能是文档的边界.如果把图像的从左到右的每一列作为一个阶段,求文档区域上边界的问题,转化求一个最长路径问题,符合动态规划分阶段、最优化原理.
|
图 3 图像的离散化表示 |
对于文档区域边界,它的起点位置不能被确定,以搜索文档区域的上边界为例,需要从左到右遍历所有的像素点,计算每个像素点的成本函数,这个成本函数值代表文档区域边界经过此像素点的可能性,用E(i, j)来表示.
考虑文档区域边界的特点,每个像素点成本函数由两部分组成,到达此点的路径最优函数C(i, j)和本身图像特征d(i, j).
根据动态规划思想,设计最优化函数为
| $ E\left( {i,j} \right) = C\left( {i,j} \right) + d\left( {i,j} \right) $ | (1) |
其中C(i, j)=max{C(i-1, l)+g(l, j)}
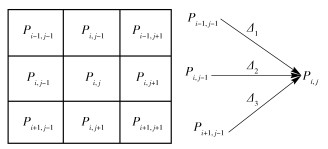
1.1 C(i, j)的计算以文档区域的上边界为例,它有以下特征:从左到右、接近水平方向.计算路径权重的时候,当前点的路径只能来自前一列相邻的元素.如图 4所示,点Pi, j,路径选择只能从它周边的8邻域中选择3邻域,左上角点Pi-1, j-1,左边点Pi, j-1,左下角点Pi+1, j-1.
|
图 4 图像像素点的邻域 |
对于像素点Pi, j,左上角点Pi-1, j-1和左下角的Pi+1, j-1点到Pi, j路径的权重相同,设定Δ1与Δ3相等.为了体现上边界的近水平的特点,左边点Pi, j-1到Pi, j路径的权重应该大于左上角点Pi-1, j-1和左下角的Pi+1, j-1点到Pi, j路径的权重,设定Δ2>(Δ1=Δ3).
| $ \left. \begin{array}{l} g\left( {{P_{i,j}},{P_{i - 1,j - 1}}} \right) = {\mathit{\Delta } _1}\\ g\left( {{P_{i,j}},{P_{i,j - 1}}} \right) = {\mathit{\Delta } _2}\\ g\left( {{P_{i,j}},{P_{i + 1,j - 1}}} \right) = {\mathit{\Delta } _3} \end{array} \right\} $ | (2) |
经过大量实验分析,Δ1、Δ2、Δ3参数的取值为Δ1=Δ3=0,Δ2=1,可以获得比较好的结果.
1.2 d(i, j)的计算对于二值图像,图像像素值只有2个值,0和1,0代表背景点,1代表前景点,文档的边界会经过最多的前景点.
| $ d\left( {i,j} \right) = \left\{ \begin{array}{l} 0,若\;{P_{i,j}} = 0\\ \theta ,若\;{P_{i,j}} = 1\left( {\theta > 0} \right) \end{array} \right. $ | (3) |
通过实验证明θ与Δ2取值相同,文档边界近水平特征与边界是前景点权重相同,可以获得比较好的结果.
在实验中,取图像上半部分的1/3作为上边界的搜索区域,从上到下,从左到右计算图像每个像素点的E(i, j).如果把E(i, j)看作像素点能量,图像能量光谱如图 5(a)所示,图 5(b)展示了最后一列每个像素的E(i, j)形成的曲线图.对最后一列的能量值,用非极大值抑制(non-maximum-suppression)求出局部的极大值,选取这些局部极大值点向左回溯得到可能的路径,如图 6(b)所示,通过局部极大值回溯的路径,有可能是多条路径,取能量值最大的3条路径.

|
图 5 图像能量光谱 |

|
图 6 边界回溯路径 |
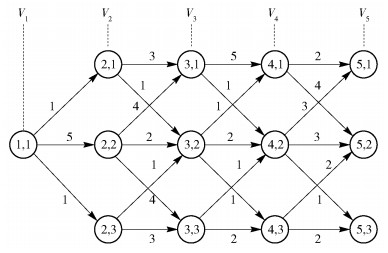
以多阶段决策图来具体说明如何通过动态规划求最长路径问题,如图 7所示, 将图划分为V1~V5 5个阶段,求文档区域边界问题,可以类似为求多段图的最长路径问题.求文档区域的上边界类似在图 7中求从V1~V5的一条最大成本的路径问题.
|
图 7 多阶段决策图 |
用C(i, j)表示路径最优函数,在C(i, j)中表示Vi,代表决策的阶段,j表示Vi阶段中的结点号,C(i, j)表示在i阶段,经过结点j的这条路径的成本.
C(i, j)的定义为
| $ C\left( {i,j} \right) = \max \left\{ {C\left( {i - 1,l} \right) + g\left( {l,j} \right)} \right\} $ | (4) |
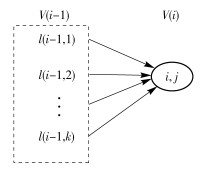
其中:l为i-1阶段与结点j相连所有结点,g(l, j)为i-1阶段所有结点与结点j连接的权重,如图 8所示.
|
图 8 g(l, j)结点的关系 |
分阶段递推结果
1) K=2阶段
| $ C\left( {2,1} \right) = g\left( {1,1} \right) = 1 $ | (5) |
| $ C\left( {2,2} \right) = g\left( {1,2} \right) = 5 $ | (6) |
| $ C\left( {2,3} \right) = g\left( {1,3} \right) = 1 $ | (7) |
2) K=3阶段
| $ \begin{array}{*{20}{c}} {C\left( {3,1} \right) = }\\ {\max \left( {C\left( {2,1} \right) + g\left( {1,1,} \right),C\left( {2,2} \right) + g\left( {2,1} \right)} \right) = }\\ {\max \left( {C\left( {2,1} \right) + 3,C\left( {2,2} \right) + 4} \right) = 9} \end{array} $ | (8) |
| $ \begin{array}{*{20}{c}} {C\left( {3,2} \right) = \max \left( {C\left( {2,1} \right) + g\left( {1,2} \right),} \right.}\\ {\left. {C\left( {2,2} \right) + g\left( {2,2} \right),C\left( {3,2} \right) + g\left( {3,2} \right)} \right) = }\\ {\max \left( {C\left( {2,1} \right) + 1,C\left( {2,2} \right) + 2,C\left( {2,3} \right) + 1} \right) = 7} \end{array} $ | (9) |
| $ \begin{array}{*{20}{c}} {C\left( {3,3} \right) = \max \left( {C\left( {2,2} \right) + g\left( {2,3} \right),} \right.}\\ {\left. {C\left( {2,3} \right) + g\left( {3,3} \right)} \right) = }\\ {\max \left( {C\left( {2,2} \right) + 4,C\left( {2,3} \right) + 3} \right) = 9} \end{array} $ | (10) |
3) K=4阶段
| $ \begin{array}{*{20}{c}} {C\left( {4,1} \right) = \max \left( {C\left( {3,1} \right) + g\left( {1,1} \right),} \right.}\\ {\left. {C\left( {3,2} \right) + g\left( {2,1} \right)} \right) = }\\ {\max \left( {C\left( {3,1} \right) + 5,C\left( {3,2} \right) + 1} \right) = 14} \end{array} $ | (14) |
| $ \begin{array}{*{20}{c}} {C\left( {4,2} \right) = \max \left( {C\left( {3,1} \right) + g\left( {1,2} \right),} \right.}\\ {\left. {C\left( {3,2} \right) + g\left( {2,2} \right),C\left( {3,3} \right) + g\left( {3,2} \right)} \right) = }\\ {\max \left( {C\left( {3,1} \right) + 4,C\left( {3,2} \right) + 3,C\left( {3,3} \right) + 4} \right) = 10} \end{array} $ | (12) |
| $ \begin{array}{*{20}{c}} {C\left( {4,3} \right) = \max \left( {C\left( {3,2} \right) + g\left( {2,3} \right),} \right.}\\ {\left. {C\left( {3,3} \right) + g\left( {3,3} \right)} \right) = }\\ {\max \left( {C\left( {3,2} \right) + 1,C\left( {3,3} \right) + 2} \right) = 8} \end{array} $ | (13) |
4) K=5阶段
| $ \begin{array}{*{20}{c}} {C\left( {5,1} \right) = \max \left( {C\left( {4,1} \right) + g\left( {1,1} \right),} \right.}\\ {\left. {C\left( {4,2} \right) + g\left( {2,1} \right)} \right) = }\\ {\max \left( {C\left( {4,1} \right) + 2,C\left( {4,2} \right) + 4} \right) = 16} \end{array} $ | (14) |
| $ \begin{array}{*{20}{c}} {C\left( {5,2} \right) = \max \left( {C\left( {4,1} \right) + g\left( {1,2} \right),} \right.}\\ {\left. {C\left( {4,2} \right) + g\left( {2,2} \right),C\left( {4,3} \right) + g\left( {3,2} \right)} \right) = }\\ {\max \left( {C\left( {4,1} \right) + 4,C\left( {4,2} \right) + 3,C\left( {4,3} \right) + 1} \right) = 18} \end{array} $ | (15) |
| $ \begin{array}{*{20}{c}} {C\left( {5,3} \right) = \max \left( {C\left( {3,2} \right) + g\left( {2,3} \right),} \right.}\\ {\left. {C\left( {3,3} \right) + g\left( {3,3} \right)} \right) = }\\ {\max \left( {C\left( {3,2} \right) + 1,C\left( {3,3} \right) + 2} \right) = 11} \end{array} $ | (16) |
在K=5阶段,最大值是C(5, 2),路径长度最大成本为18.通过向后回溯,求最长路径经过的结点.
在式(15) 中,使C(5, 2) 取得最大值是C(4, 1),在K=4阶段中,能使C(4, 1) 取得最大值是C(3, 1),在K=3阶段中,能使C(3, 1) 取得最大值是C(2, 2),回溯求得的路径是:(5, 2), (4, 1), (3, 1), (2, 2), (1, 1).
1.4 文档边界检测算法流程1) 图像宽度为M(m=1, 2, …, M),高度为N(n=1, 2, …, N),第1列所有结点的初始能量C(Pi, 1)=D(Pi, 1)(i=1, 2, …, n).
2) 对于所有的m=1, 2, …, M重复步骤3).
3) 在图像中m列的(n, n)点,对于前m-1列,重复步骤4).
4) 设
| $ E\left( {i,j} \right) = \mathop {\max }\limits_i \left[ {E\left( {i - 1,j} \right) + g\left( {l,j} \right)} \right] + d\left( {i,j} \right) $ | (17) |
5) 求最后一列像素的能量函数E(Pi, M,i=1, 2, …, n, 通过极大抑制算法[11],求出能量值为局部极大值的点,从这些局部极大值点回溯得到的路径,有可能是文档区域的边界,但是回溯的路径有可能多条.
2 边界组合算法对于文档区域的上、下、左、右4个边界,分别通过动态规划算法来检测,由于手机拍照图像的质量不高,通过动态规划回溯的路径可能不仅仅是一条,一般的原则保留1~3条路径作为候选.如果要确定一条路径是否是文档的区域,要通过其他边界关联来确定,因为只有4条边界合理组合,才能形成文档区域.假定每条边界有3条候选边,则可能形成(3×3×3×3=81)81个组合,为了快速判定一个组合是文档区域,通过逻辑回归的二分类算法来处理这个问题.
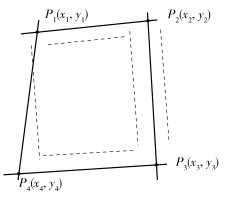
通过动态规划算法检测的路径,由离散的点组成,这些点未必在一条直线上,通过直线拟合算法,把检测到的文档区域的边界转化为直线,求得4条边界的交点:P1(x1, y1), P2(x2, y2), P3(x3, y3), P4(x4, y4), 如图 9所示.
|
图 9 文档区域的边界交点 |
如果4条边界形成了文档区域,则这些边界有下列特点:
相对的2个边接近平行,180°±30°,平行特征:x1;
相对的2个边距离相对较远,距离特征:x2;
相临边的角度接近90°±30°,角度特征:x3;
组成四边形面积大于整个图像面积60%,面积特征:x4.
1) 根据上述特征设计逻辑回归的假设函数
| $ {h_\theta }\left( x \right) = {\theta _0} + {\theta _1}{x_1} + {\theta _2}{x_2} + {\theta _3}{x_3} + {\theta _4}{x_4} $ |
因变量用hθ(x):
hθ(x)=1,是文档区域边界.
hθ(x)=0,非文档区域边界.
自变量x1, x2, x3, x4计算如下:
| $ {x_1} = \left( {\frac{{\left| {{y_2} - {y_1}} \right|}}{{\left| {{x_2} - {x_1}} \right|}} - \frac{{\left| {{y_3} - {y_4}} \right|}}{{\left| {{x_3} - {x_4}} \right|}}} \right)\left( {\frac{{\left| {{y_4} - {y_1}} \right|}}{{\left| {{x_4} - {x_1}} \right|}} - \frac{{\left| {{y_3} - {y_2}} \right|}}{{\left| {{x_3} - {x_2}} \right|}}} \right) $ | (18) |
| $ {x_2} = \frac{{\left| {{x_2} - {x_1}} \right| + \left| {{x_3} - {x_4}} \right|}}{{2w}} $ | (19) |
其中w为图像宽度
| $ {x_3} = {\tan ^{ - 1}}\frac{{{y_1}}}{{{x_1}}} - {\tan ^{ - 1}}\frac{{{y_2}}}{{{x_2}}} $ | (20) |
| $ {x_4} = \frac{{\left| {\begin{array}{*{20}{c}} {{x_1}}&{{y_1}}&1\\ {{x_2}}&{{y_2}}&1\\ {{x_3}}&{{y_3}}&2 \end{array}} \right| + \left| {\begin{array}{*{20}{c}} {{x_1}}&{{y_1}}&1\\ {{x_2}}&{{y_2}}&1\\ {{x_4}}&{{y_4}}&1 \end{array}} \right|}}{{wh}} $ | (21) |
其中w、h分别为图像宽度和高度.
2) 建立价值函数
| $ J\left( \theta \right) = \frac{1}{2}\sum\limits_{i = 1}^m {\left( {{h_\theta }{{\left( {{x^{\left( i \right)}} - {y^{\left( i \right)}}} \right)}^2}} \right.} $ |
3) 用梯度下降法不断修正θ值,直至收敛.
| $ {\theta _j}: = {\theta _j} - \alpha \frac{{{\partial _j}\left( \theta \right)}}{{\partial {\theta _j}}} $ |
其中α为学习速率.
4) 求得最终(θ0, θ1, θ2, θ3, θ4)
通过1 000个正样本和1 000个负样本,利用Matlab工具箱逻辑回归函数,计算出
| $ \begin{array}{*{20}{c}} {{h_\theta }\left( x \right) = 0.0347 + 0.1867{x_1} - 1.6754{x_2} + }\\ {0.07896{x_3} + 0.02367{x_4}} \end{array} $ |
PC机的配置:酷睿双核i5处理器,主频2.7 GHz,内存32 GB.
1) 边界检测测试
对不同场景下图片,包括清晰、模糊、非水平畸变、光照不均匀的情况进行测试.统计边界检测的准确率和运行时间.
测试图片的总数量:4 000张
清晰的图片:1 000张
比较模糊图像:1 000张
光照不均匀:1 000张
非水平畸变:1 000张
测试图像分辨率大小:1 600×1 200,从以下2个方面测试算法效果.
找边成功率:能从背景图像中找到候选的边,每个边界取TOP 3, 即0~3个边.
运行时间:检测到文档区域边界的时间.
测试结果如表 1所示.
|
|
表 1 PC机上测试结果 |
2) 边界组合测试
输入自变量x1、x2、x3、x4, 通过二分类的逻辑回归算法计算hθ(x)=θ0+θ1x1+θ2x2+θ3x3+θ4x4,判定选定的4个边是否为文档区域.测试结果如表 2所示.
|
|
表 2 逻辑回归的判定结果 |
测试方法:模拟用户的拍照场景,测试图像数据来源手机拍照的视频流.
手机型号:华为DIG-AL00
CPU型号:骁龙435(MSM8940)
CPU参数:八核,1.4 GHz
存储ROM:32 GB,RAM:3 GB
边界检测算法在手机上运行,速度非常重要,如果边界检测的速度较慢,用户感觉反应迟钝,体验效果差.为了提高边界检测的速度,图像大小缩放到800×600.与网易的有道云笔记[12]相比,确定文档区域边界的准确率和运行速度超过同类产品, 测试结果如表 3所示.
|
|
表 3 手机上测试结果 |
在手机上测试算法的准确率低于PC上准确率,主要有以下原因:
1) 在测试过程中,手机处于运动状态,手机的焦距不准,模糊图像所占的比例比较大;
2) 手机拍照过程中,不断地调整相机的角度和远近,由于图像是实时抓取,有些视频流图像帧中包含部分文档的区域,文档区域的边界不完整,边界检测的失败率比较高;
3) 测试数据中准确率,不仅包含边界检测算法,而且包含边界组合的算法.
在实际应用场景下,手机上找边过程与用户是实时交互的,用户可以判断找边是否准确,当找边运算速度达到10帧/s,这个准确率是完全可以满足用户拍照需求的.
4 结束语通过实验证明,动态规划算法可以很好地解决手机拍照图像的文档区域边界检测问题,用逻辑回归的二分类算法解决边界组合问题.但是对于动态规划中的路径权重分配以及参数选择问题如何做到最优是下一步要重点研究的问题.
| [1] | Duda R O, Hart P E. Using hough transform to detect lines and curves in pictures[J]. Communications of the ACM, 1972, 15(1): 11–15. doi: 10.1145/361237.361242 |
| [2] | Xu L, Oja E. Randomized hough transform (RHT):basic mechanisms, algorithms, and computational complexities[J]. CVGIP:Image Understanding, 1993, 57(2): 131–154. doi: 10.1006/ciun.1993.1009 |
| [3] | Zhang Zhenyou, Li Weihe. White board scanning and image enhancement[J]. Digital Signal Processing, 2007, 17(2): 414–432. doi: 10.1016/j.dsp.2006.05.006 |
| [4] |
孙丰容, 刘积仁. 快速霍夫变换算法[J]. 计算机学报, 2001, 24(10): 1102–1109.
Sun Fengrong, Liu Jiren. Fast Hough transform algorithm[J]. Journal of Computer Science, 2001, 24(10): 1102–1109. doi: 10.3321/j.issn:0254-4164.2001.10.013 |
| [5] | Bellmann R E. Dynamic programming[M]. Princeton, NJ: Princeton University Press, 1957. |
| [6] | Amini A A. Using dynamic programming for solving variational problems in vision[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1990, 12(9): 855–867. doi: 10.1109/34.57681 |
| [7] | Sonka M, Hlavac V. Image processing, analysis and machine vision[J]. Journal of Electronic Imaging, 2008(82): 685–686. |
| [8] | Merlet N, Zerubia J. New prospects in line detection by dynamic programming[J]. IEEE Transactions on Pattern Analysis and machine intelligence, 1996, 18(4): 426–431. doi: 10.1109/34.491623 |
| [9] | Ungru K, Jiang X Y. Dynamic programming based segmentation in biomedical imaging[J]. Computational and Structural Biotechnology Journal, 2017(15): 255–264. |
| [10] | Rosado-Toro J A. Dynamic programming using polar variance for image segmentation[J]. IEEE Transactions on Image Processing, 2016, 25(12): 5857–5866. doi: 10.1109/TIP.2016.2615809 |
| [11] | Zaytseva E, Vitrià J. A search based approach to non maximum suppression in face detection[C]//201219th IEEE International Conference on Image Processing. 2012:1469-1472. |
| [12] | 北京网易有道计算机系统有限公司. 有道云笔记[EB/OL]. (2017-05-10)[2017-06-10]. http://note.youdao.com/download.html#androi. |


