2. 西安交通大学 电子与信息工程学院, 西安 710049;
3. 西安邮电大学 通信与信息工程学院, 西安 710061
针对大多数基于距离和密度的异常检测算法敏感于近邻参数k的问题,提出了一种鲁棒性异常检测标准——k-近邻域中心偏移异常因子(COOF).数据结点的k-近邻域中心位置会随着近邻参数k的变化而发生迁移,鉴于异常结点要比正常结点对k-近邻域中心位置偏移量的影响更大,通过累加因递增k而产生的偏移量来表征数据结点的异常程度,并在COOF基础上实现了鲁棒性的异常检测算法.通过综合数据和真实数据的实验仿真可知,COOF不仅对近邻参数k具有鲁棒性,而且相比基于距离的k最近邻算法、基于局部距离的异常因子和基于密度的局部异常因子具有更稳定且更准确的异常检测性能.
2. School of Electronic and Information Engineering, Xi'an Jiaotong University, Xi'an 710049, China;
3. School of Communication and Information Engineering, Xi'an University of Posts and Telecommunications, Xi'an 710061, China
Considering the distance-and density-based outlier detection algorithms are often sensitive to a nearest neighbor parameter k, termed k-center offset outlier factor (COOF), a robust outlier detection criterion for the characterization of abnormal degree of each data object was proposed. Each data object is included in a region within its k nearest neighbors, and the center of region will migrate with the change of nearest neighbor parameter k. In general, the variation of center offset of k nearest neighbor region is greater for an outlier than a normal object. According to this observation, for each data object, COOF is defined as the accumulation of this kind of offset when increasing the nearest neighbor parameter from one to k. Finally, the outlier detection algorithm based on COOF was also presented. Through artificial data and real data experimental simulations show that COOF is insensitive to parameter k, and has more stable and accurate outlier detection performance compared to k nearest neighbor, local distance-based outlier factor and local outlier factor, which are the distance-based method and density-based method respectively.
异常检测是数据挖掘领域中的一个重要分支,旨在从数据集中挖掘出那些不符合正常数据特征的少数结点.通过挖掘少数但关键的隐藏特征信息,异常检测已被多种社会应用所采纳,包括信用卡欺诈检测、电子商务犯罪活动发现、图像处理、视频监控、天气预报、医药研究[1]等,以及基于软件定义网络的流量异常检测相关研究[2].
目前异常挖掘算法[3]主要包括2类:监督性和非监督性异常挖掘.监督性异常挖掘算法需要大量样本进行模型测试,但实际应用中无法事先获取大量训练样本.对于非监督性异常挖掘算法,主要划分为2类:基于距离和基于密度的异常检测算法. k最近邻(KNN, k nearest neighbor)[4]是一种典型的基于距离的异常检测算法,利用数据结点的第k-近邻距离作为异常程度高低的判别因子,然而这类方法往往受限于局部密度问题[5].基于密度的异常检测算法通过比较数据结点和其近邻结点的局部密度来评价其异常程度,代表算法是局部异常因子(LOF, local outlier factor),虽然此类算法解决了局部密度问题,但是无法有效处理低密度模式问题[6].总结来说,这2类检测算法无法同时考虑数据结点的全局和局部特征,近邻参数k过小无法准确识别全局异常点;相反,k过大无法准确识别局部异常点.
针对上述问题,笔者提出一种基于k-近邻域中心偏移异常因子(COOF, center offset outlier factor)来表征数据结点的异常程度,进而实现鲁棒性的异常检测算法.随着近邻参数k的变化,基于异常结点的k-近邻域中心偏移程度要远大于正常结点的k-近邻域中心偏移程度.根据这一性质,COOF通过累加因递增k而产生的k-近邻域中心偏移量来表征数据结点的异常程度.最后通过在综合数据和真实数据上进行实验仿真得出COOF不仅能解决近邻参数的敏感性问题并提供稳定的异常检测结果,而且在同时考虑检测准确度和受试者工作特征曲线的面积(AUC, Area Under Curve)[7]2种评价标准时,其性能均优于KNN、基于局部距离的异常因子(LDOF, Local distance-based outlier factor)和LOF算法.
1 异常检测问题对于绝大多数非监督性异常挖掘算法,异常因子的高低直接表达了数据结点异常程度的高低,一般来说异常因子较高的数据结点成为异常结点的可能性更大.下面分别介绍典型的基于距离的异常检测算法KNN[4]和LDOF[8],以及基于密度的异常检测算法LOF[5].
定义1 对象p的k-近邻距离.对于任意正整数k,对象p的k-近邻距离表示为dk(p),定义为对象p和o之间的距离d(p, o),必须同时满足以下2个条件:
1) 数据集D中至少存在k个对象o′∈D\{p}满足d(p, o′)≤d(p, o);
2) 数据集D中至多存在k-1个对象o′∈D\{p}满足d(p, o′)<d(p, o).
其中{p, o}∈D,距离度量方式可以是欧几里得距离、曼哈顿距离或其他任意一种相异性度量方式.
定义2 Nk(p)表示对象p的k-近邻域,表示为
| ${N_k}\left( p \right) = \left\{ {q\left| {d\left( {p,q} \right) \le {d_k}} \right.\left( p \right),q \ne p} \right\}$ | (1) |
其中d(p, q)为数据集D中对象p和q间的直达距离.
Ramaswamy等[4]提出的KNN作为基于距离的异常检测算法代表,利用数据结点和其第k-近邻结点间的距离量化其异常程度.给定一个数据结点p和其k-近邻距离dk(p),那么其异常因子fKNN(p)表示为p和其第k-近邻结点间的距离:
| ${f_{{\rm{KNN}}}}\left( p \right) = {d_k}\left( p \right)$ | (2) |
Breunig等[5]提出的LOF是一种典型的基于密度的异常检测算法,利用异常结点周围的密度往往低于其近邻的密度这一事实,计算出每个数据结点的局部异常因子,一般LOF(p)越高表示数据结点p成为异常结点的可能性越大.给定数据结点p和正整数k,异常因子fLOF(p)表示为
| ${f_{{\rm{LOF}}}}\left( p \right) = \frac{1}{{\left| {{N_k}\left( p \right)} \right|}}\sum\limits_{q \in {N_k}\left( p \right)} {\frac{{{l_k}\left( q \right)}}{{{l_k}\left( p \right)}}} $ | (3) |
其中:lk(p)为数据结点p的直接可达密度,通过计算p和q(q∈Nk(p))之间平均可达距离的倒数得到,Nk(p)表示结点p的k-近邻域.
Zhang等[8]提出的LDOF是另一种基于距离的局部异常检测因子,LDOF利用数据结点与其近邻之间的相对距离来度量偏离其散列近邻的程度,偏离程度越大则表明是异常结点的可能性也更大.给定数据结点p和正整数k,异常因子fLDOF(p)定义为
| $\begin{array}{l} \quad \quad \quad {f_{{\rm{LDOF}}}}\left( p \right) = \bar d/\bar D = \\ \frac{{\frac{1}{k}\sum\limits_{q \in {N_k}\left( p \right)} {d\left( {p,q} \right)} }}{{\frac{1}{{k\left( {k - 1} \right)}}}}\sum\limits_{p,q \in {N_k}\left( p \right),p \ne q} {d\left( {p,q} \right)} \end{array}$ | (4) |
其中d(p, q)为数据结点p和q之间的距离.
1 异常检测模型 2.1 COOF定义立体几何中的四脚椎体是一种典型的四面体结构,因其具有重心低和稳定性强的特点作为防波堤结构应用于海岸工程,主要优势在于四脚椎体的重心低,而表面离重心点越近则越不会因外力驱动而发生畸形.同理,在异常结点挖掘中,如果一个数据结点远离其邻域重心程度越大表明其是异常结点的可能性更大.由于数据区域不存在质量分布问题,数据区域重心即为数据区域中心,计算见式(5).
假设存在μ个离散数据点(xi, yi)(i=1, 2, …, μ),则其覆盖μ个数据结点的区域中心G(
| $\left. {\begin{array}{*{20}{c}} {\tilde x = \frac{{\sum\limits_{i = 1}^\mu {{x_i}} }}{\mu }}\\ {\tilde y = \frac{{\sum\limits_{i = 1}^\mu {{y_i}} }}{\mu }} \end{array}} \right\}$ | (5) |
这种方法最为简单直观,直接利用离散数据点的横纵坐标即可求得覆盖区域的数据中心.给定数据结点p,其k-近邻区域为Nk(p),则p的k-近邻区域Nk(p)的区域中心表示为
| ${c_k}\left( p \right) = \frac{1}{k}\sum\limits_{q \in {N_k}\left( p \right)} {{\mathit{\boldsymbol{x}}_q}} $ | (6) |
其中xq=(xq1, xq2, …, xqn)∈
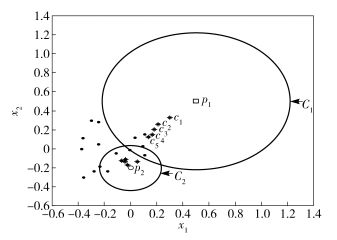
图 1展示了k-近邻域中心偏移范例,可看出通过递增k,数据结点的k-近邻域中心发生了迁移.对于正常结点p2来说,伴随着k的变化,其中心ck(p2)的变化微小,其中C2表示p2结点在k=5时的近邻域.而对于异常结点p1来说,伴随着k的递增,其中心ck(p1)却发生了明显的迁移变化,图 1中c1, c2, c3, c4, c5标识了k从1变化至5时,p1结点的k-近邻域中心位置变化过程,其中C1表示异常点p1在k=5时的近邻域.通过量化数据结点的k-近邻域中心位置变化造成的距离偏移来表征数据结点的异常程度.
|
图 1 k-近邻域中心偏移范例 |
对于数据结点p,伴随着k的自增,其k-近邻域中心的迁移量表示为
| ${\sigma _i}\left( p \right) = d\left( {{c_i}\left( p \right),{c_{i + 1}}\left( p \right)} \right),i = 1,2, \cdots ,k - 1$ | (7) |
为了强调表示k对数据结点的k-近邻域中心位置的影响,采用中心迁移量的绝对误差来定义其k-近邻中心位置变化的抖动程度.最后,通过累加数据结点k-近邻域中心位置迁移的波动程度定义出COOF:
| ${f_{{\rm{COOF}}}}\left( p \right) = \sum\limits_{i = 1}^{k - 2} {\left| {{\sigma _i}\left( p \right) - {\sigma _{i + 1}}\left( p \right)} \right|} $ | (8) |
本节详细介绍基于COOF的异常检测算法流程,如算法1所示.首先计算每个数据结点的COOF,通过排序得到具有最高异常因子的异常结点.为了充分考虑所有数据结点的全局和局部特征,按照LOF算法对近邻参数k的定义范围[5],COOF选择其上界作为算法输入.
算法1 基于COOF的异常检测算法
输入:数据集D,近邻数k,异常结点数m
输出:具有最高COOF值的m个异常结点
1 for p∈D do
2 for i=1 to k do
3 根据p的k-近邻距离dk(p)定义Nk(p);
4 计算p的k-近邻域Nk(p)的中心ck(p):
ck(p)=
5 计算Nk(p)的中心位置绝对偏移量Δσi(p):
Δσi(p)=d(ci(p), ci+1(p))-d(ci+1(p), ci+2(p))
6 end for
7 计算fCOOF(p)=
8 排序f′COOF←Sort(fCOOF, descending);
9end for
10 return具有最高COOF的m个异常结点.
3 仿真实验 3.1 评价指标针对异常检测算法的性能评估,将采用准确度和受试者工作特征曲线(ROC, receiver operating characteristic curve)[7]来综合评估数据集的异常检测结果.基于异常检测的准确度EAcc定义为
| ${E_{{\rm{Acc}}}} = \frac{n}{m}$ | (9) |
其中:m为原始数据中的真实异常结点数,n为检测到的真实异常结点数.
考虑到样本数据的不均衡分布问题,补充采用ROC来评价异常检测结果.而AUC作为ROC的定量统计可以直观地表达出分类性能的高低,一般来说AUC值越高表示分类器性能越好. AUC[7]的定义为
| ${E_{{\rm{AUC}}}} = \left( {{S_0} - \frac{{{n_0}({n_0} + 1)}}{2}} \right)/{n_0}{n_1}$ | (10) |
其中:n0和n1分别为正常样本数和异常样本数;S0= ∑ ri,ri为在按样本所述类别概率进行排序后第i个正常样本的排序位置.
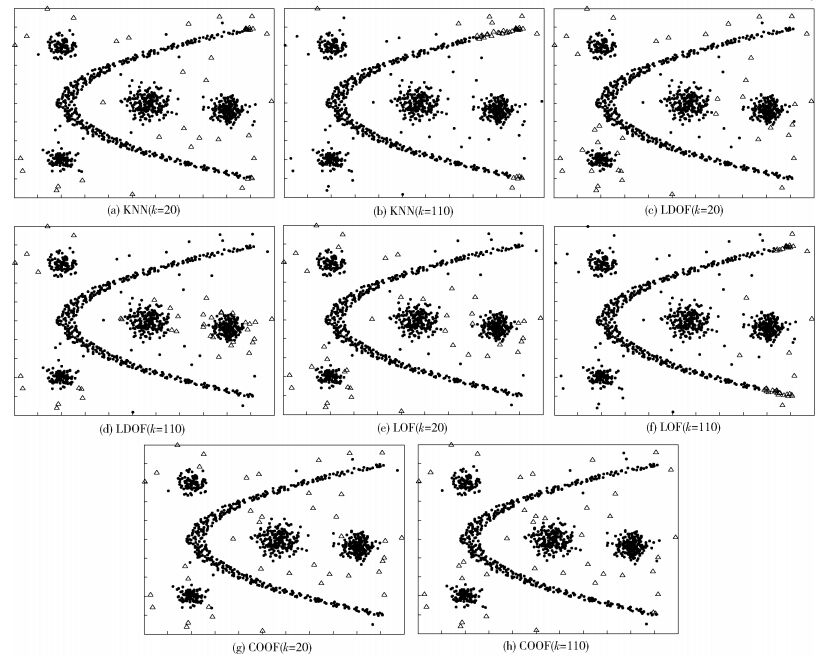
3.2 综合数据检测本节将讨论COOF对比KNN、LOF和LDOF算法在综合数据中的异常检测性能. 图 2所示的综合数据D同时包含了局部密度[5]和低密度模式[6]特征的数据集,一共包含1 140个数据结点,划分为5个类簇,分别是抛物线状和4个高斯分布类簇.抛物线分布的数据结点数是400,4个高斯分布类簇满足自相关矩阵Σt=tI2×2,其中I2×2为2×2单位矩阵,t=0.05, 0.03, 0.02, 0.02为数据分布的离散度.这4个高斯类簇所包含的数据结点数分别是200、200、100、100,另外随机产生40个异常数据结点添加到D中.基于该综合数据集D,通过改变近邻数k来对比KNN、LOF、LDOF和COOF在异常检测中的性能.对于这4种方法,通过异常检测得到40个具有最高异常因子的异常结点.从图 2中可看出,当k=20时,这4种方法均表现出较好的异常检测结果;但当k=110时,KNN、LDOF和LOF出现较大的检测误差,而COOF却依然能保持较高精度的异常检测性能.
|
图 2 综合数据集异常检测结果 |
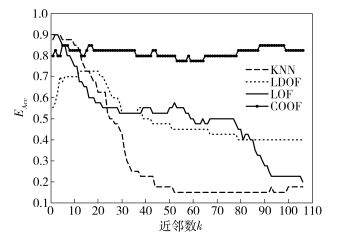
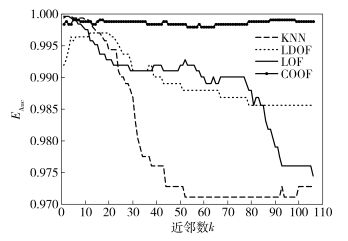
对于KNN和LDOF这类基于距离的异常检测算法,当k值递增时,倾向于检测“全局异常”结点,直观地解释为“全局异常”结点容易被KNN和LDOF检测到,但局部异常结点却容易被忽视.而对于LOF算法,考虑图 2(c)中左下角类簇中的数据结点,由于离其最近的类簇大致包含100个数据结点,当k增长时,其k-近邻结点逐渐考虑到密度更小的抛物线数据集.因此,LOF不能准确发现高密度类簇周围的真实异常结点,却反而把低密度类簇中的结点误认为异常结点.另外,图 3和图 4分别展示了k值在递增过程中异常检测指标的变化过程. 4种算法在k值较小时均表现出了高效的检测性能.然而,随着k值的递增,KNN、LDOF和LOF检测性能下降明显,但是所提出的COOF却依然保持高检测性能.
|
图 3 准确度对比结果 |
|
图 4 AUC对比结果 |
笔者同时将COOF应用到2种真实网络数据集Iris和Wine中,均来源于UCI机器学习库[9]. Iris数据集一共包含150个实例,每个实例包括4维属性,所有实例划分为3类,类标签分别是setosa、versicolour和virginica. Wine数据集一共包含178个实例,每个实例包括13维属性,所有实例也划分为3类(Class 1、Class 2和Class 3).针对这2种数据集,实验中分别选择其中任意2个类簇的数据作为正类数据点,从剩下的一类中任意选择5个数据点作为异常结点.
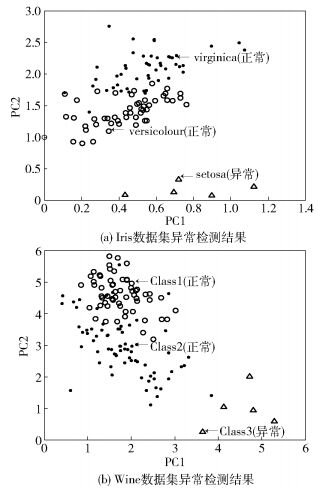
由于这2种数据集均是高维数据集,为便于在二维坐标系中可视化展示异常检测结果,因此采用非负矩阵分解[10]算法对数据进行降维处理,从而提取能够反映原始数据主特征的二维属性,然后根据这二维属性构建二维可视化坐标系. 图 5展示了经降维处理过的数据集应用COOF进行异常检测的结果,横纵坐标分别表示2个主成分(PC1和PC2).其中上三角代表检测到的异常结点,而空心圆和实心点代表正常结点,可看出COOF同样可以很准确地检测出数据集中的真实异常结点.
|
图 5 基于COOF的真实数据集异常检测结果 |
在利用KNN、LDOF、LOF和COOF 4种算法进行真实数据集的异常检测时,首先计算每个结点的异常因子,然后将具有最高异常因子的5个数据结点标识为异常结点,具体检测结果如表 1所示.从表 1中总结得出LDOF和LOF两种算法的检测性能随着k值变化发生了较大改变,而COOF算法却基本保持稳定且具有较高的准确度和AUC.由于Wine和Iris这2种数据集的数据分布特征较为简单,不存在密度差异较大的类簇,因此KNN算法也表现出了较高的检测性能.但如图 2所示在具有密度差异较大的数据集中,KNN检测性能下降明显,而COOF依然表现出高检测性能.
|
|
表 1 检测性能 |
笔者提出了一种基于k-近邻域“中心偏移的鲁棒性异常检测算法”,利用数据结点的k-近邻区域中心位置偏移量来定义一种新的表征结点异常程度的异常因子,而具有较高COOF的结点代表异常结点的可能性更大.基于COOF的异常检测算法不敏感于近邻参数k的选择,能够同时考虑数据结点的全局和局部特征.通过综合数据和真实数据的实验仿真得出COOF不仅能实现模型参数k的鲁棒性选择,而且相比于KNN、LDOF和LOF检测算法具有更稳定且更准确的异常检测性能.
| [1] | Ha J, Seok S, Lee J S. A precise ranking method for outlier detection[J]. Information Sciences, 2015, 324: 88–107. doi: 10.1016/j.ins.2015.06.030 |
| [2] |
左青云, 陈鸣, 王秀磊, 等. 一种基于SDN的在线流量异常检测方法[J]. 西安电子科技大学学报, 2015, 42(1): 155–160.
Zuo Qingyun, Chen ming, Wang Xiulei, et al. Online traffic anomaly detection method for SDN[J]. Journal of Xidian University, 2015, 42(1): 155–160. |
| [3] |
刘敬, 谷利泽, 钮心忻, 等. 基于单分类支持向量机和主动学习的网络异常检测研究[J]. 通信学报, 2015, 36(11): 136–146.
Liu Jing, Gu Lize, Niu Xinxin, et al. Research on network anomaly detection based on one-class SVM and active learning[J]. Journal on Communications, 2015, 36(11): 136–146. doi: 10.11959/j.issn.1000-436x.2015252 |
| [4] | Ramaswamy S, Rastogi R, Shim K. Efficient algorithms for mining outliers from large data sets[J]. ACM SIGMOD Record, 2000, 29(2): 427–438. doi: 10.1145/335191 |
| [5] | Breunig M M, Kriegel H P, Ng R T, et al. LOF:identifying density-based local outliers[J]. ACM SIGMOD record, 2000, 29(2): 93–104. doi: 10.1145/335191 |
| [6] | Tang Jian, Chen Zhixiang, AW Fu, et al. Enhancing effectiveness of outlier detections for low density patterns[C]//Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining. Berlin:Springer-Verlag, 2002:535-548. |
| [7] | Huang Jin, Ling Charles X. Using AUC and accuracy in evaluating learning algorithms[J]. IEEE Transactions on Knowledge & Data Engineering, 2005, 17(3): 299–310. |
| [8] | Zhang Ke, Hutter Marcus, Jin Huidong. A new local distance-based outlier detection approach for scattered real-world data[C]//Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining. Berlin:Springer-Verlag, 2009:813-822. |
| [9] | UCI. UCI Repository of Machine Learning Databases[EB/OL]. Irvine, CA:University of California(2007)[2007]. http://www.ics.uci.edu/~mlearn/MLRepository.html. |
| [10] | Lee D D, Seung H S. Learning the parts of objects by non-negative matrix factorization[J]. Nature, 1999, 401(6755): 788. doi: 10.1038/44565 |


