2. 北京航空航天大学 可靠性与环境工程技术重点实验室, 北京 100191;
3. 北京邮电大学 自动化学院, 北京 100876
为解决机械臂运动轨迹可靠性分析的计算效率和精确性难题,提出自更新响应面法分析机械臂运动轨迹可靠性.首先,根据等效极值思想,将机械臂的运动轨迹可靠性转换为运动误差最大时的轨迹点可靠性;其次,基于粒子群优化算法,求解随机输入在不同样本情况下运动误差达到最大时所对应的时间,利用这些数据构建关于时间的Kriging响应面,在可靠性分析过程中,通过该响应面快速预估机械臂运动误差最大时所对应的时间,以此提高计算效率;第三,基于相对均方预估误差建立自更新机制,通过加入新的样本点来提升Kriging响应面的近似精度,确保可靠性分析结果的精确性.最后,通过案例分析验证所提方法的有效性和正确性.
2. Science and Technology on Reliability and Environmental Engineering Laboratory, Beihang University, Beijing 100191, China;
3. School of Automation, Beijing University of Posts and Telecommunications, Beijing 100876, China
In order to solve the efficiency and accuracy problem appeared in motion trajectory reliability analysis of the manipulator, a new automatic updating response surface method is presented. Firstly, based on the equivalent extreme value approach, the motion trajectory reliability analysis is converted into the reliability analysis about the trajectory point in which the motion error reaches its maximum. Secondly, for different random sample inputs, the particle swarm optimization algorithm is employed to get the time responses corresponding to the maximum values of the motion errors. These inputs and time responses are used to construct a Kriging response surface of time, which is used to get the estimated value of the time response rapidly and improve the efficiency of the reliability analysis. Thirdly, based on the mean square predicted error, an automatic updating mechanism is constructed. Through adding new sample points, the approximate quality of the Kriging response surface is improved, and the accuracy of the reliability analysis results is assured. A case analysis is used to demonstrate the validity of the proposed method.
运动精度是机械臂完成任务的基础[1],分析其运动可靠性,对提高机械臂工作能力有着切实意义.
机械臂运动可靠性分为运动轨迹可靠性和轨迹点可靠性[2],前者更具实际意义,常使用首次穿越法和PHI2法进行分析[3-4],但计算精度不足,蒙特卡罗法(MCM, Monte Carlo method)的效率偏低.
针对计算效率与精确性难题,提出自更新响应面法分析机械臂的运动轨迹可靠性.借鉴等效极值思想[5-6],将运动轨迹可靠性转换为具有最大运动误差的轨迹点可靠性,通过构建Kriging响应面快速预估运动误差达到最大时所对应的时间,建立自更新机制提升响应面近似精度,确保分析结果精确性.
1 机械臂运动轨迹可靠性模型 1.1 影响机械臂运动精度的随机因素影响机械臂运动精度的随机因素种类繁杂,例如,关节间隙、装配精度等,这些因素通过作用于机械臂的关节角度和几何参数,间接影响其运动精度.根据Denavit-Hartenberg法(D-H)可得到[7]:
| $ \mathit{\boldsymbol{T}}_{i - 1}^i = \left[ {\begin{array}{*{20}{c}} {\cos \left( {{\theta _i}} \right)}&{ - \sin \left( {{\theta _i}} \right)\cos \left( {{\alpha _{i - 1}}} \right)}&{\sin \left( {{\theta _i}} \right)\sin \left( {{\alpha _{i - 1}}} \right)}&{{a_{i - 1}}\cos \left( {{\theta _i}} \right)}\\ {\sin \left( {{\theta _i}} \right)}&{\cos \left( {{\theta _i}} \right)\cos \left( {{\alpha _i}} \right)}&{ - \cos \left( {{\theta _i}} \right)\sin \left( {{\alpha _{i - 1}}} \right)}&{{a_{i - 1}}\sin \left( {{\theta _i}} \right)}\\ 0&{\sin \left( {{\alpha _{i - 1}}} \right)}&{\cos \left( {{\alpha _{i - 1}}} \right)}&{{d_i}}\\ 0&0&0&1 \end{array}} \right] $ | (1) |
| $ \mathit{\boldsymbol{T}} = \mathit{\boldsymbol{T}}_0^1\mathit{\boldsymbol{T}}_1^2, \cdots ,\mathit{\boldsymbol{T}}_{n - 1}^n $ | (2) |
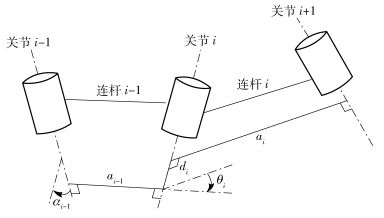
其中:n为机械臂关节数目,Ti-1i为关节坐标系i-1相对坐标系i的变换矩阵,T为基座坐标系相对末端坐标系的变换矩阵,D-H参数ai-1、αi-1、di以及θi分别为连杆i-1的长度、连杆i-1的扭角、连杆i相对于连杆i-1的偏置以及连杆i-1与连杆i之间的关节角,如图 1中所示. D-H参数体现了几何参数和关节角度信息,其误差将直接影响运动精度.
|
图 1 D-H运动学参数示意图 |
设向量p和η分别为机械臂基坐标系相对末端坐标系的位置和姿态误差,表示为[8]
| $ \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{p}}\\ \mathit{\boldsymbol{\eta }} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{K}}_1}}&{{\mathit{\boldsymbol{K}}_2}}&{{\mathit{\boldsymbol{K}}_3}}&{{\mathit{\boldsymbol{K}}_4}}\\ {{\mathit{\boldsymbol{K}}_5}}&{{{\bf{0}}_{3 \times n}}}&{{{\bf{0}}_{3 \times n}}}&{{\mathit{\boldsymbol{K}}_6}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\Delta \mathit{\boldsymbol{\alpha }}}\\ {\Delta \mathit{\boldsymbol{a}}}\\ {\Delta \mathit{\boldsymbol{a}}}\\ {\Delta \mathit{\boldsymbol{\theta }}} \end{array}} \right] $ | (3) |
其中:03×n为3×n矩阵,Δα、Δa、Δd以及Δθ分别为D-H参数α=[α0, α1, …, αn-1]T、a=[a0, a1, …, an-1]T、d=[d1, d2, …, dn]T以及θ=[θ1, θ2, …, θn]T的微小随机误差.
式(3) 中的系数矩阵Kj(j=1, 2, 3, 4) 表示为[8]
| $ \left. {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{K}}_1^i = {{\left( {{\mathit{\boldsymbol{A}}_{i + 1}} \times {\mathit{\boldsymbol{C}}_{i + 1}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{q}}_i^4}\\ {\mathit{\boldsymbol{K}}_2^i = {{\left( {{\mathit{\boldsymbol{C}}_{i + 1}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{q}}_i^1}\\ {\mathit{\boldsymbol{K}}_3^i = {{\left( {{\mathit{\boldsymbol{C}}_{i + 1}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{q}}_i^2}\\ {\mathit{\boldsymbol{K}}_4^i = {{\left( {{\mathit{\boldsymbol{A}}_{i + 1}} \times {\mathit{\boldsymbol{C}}_{i + 1}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{q}}_i^5 + {{\left( {{\mathit{\boldsymbol{C}}_{i + 1}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{q}}_i^3}\\ {i = 1,2, \cdots ,n} \end{array}} \right\} $ | (4) |
其中:qi1=[1, 0, 0]T、qi2=[0, sin(αi-1), cos(αi-1)]T、qi3=[0, ai-1cos(αi-1), -ai-1sin(αi-1)]T、qi4=[1, 0, 0]T、qi5=[0, sin(αi-1), cos(αi-1)]T.矩阵Ai+1和Ci+1可根据下式计算[9]:
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{C}}_i}}&{{\mathit{\boldsymbol{A}}_i}}\\ {{{\bf{0}}_{3 \times 3}}}&1 \end{array}} \right] = \mathit{\boldsymbol{T}}_{i - 1}^i\mathit{\boldsymbol{T}}_i^{i + 1} \cdots \mathit{\boldsymbol{T}}_{n - 1}^n,i = 1,2, \cdots ,n $ | (5) |
结合式(3)~(5),可得到机械臂末端期望位置与实际位置的误差表达式:
| $ {\left\| \mathit{\boldsymbol{p}} \right\|_2} = {\left\| {{\mathit{\boldsymbol{K}}_1} \cdot \Delta \mathit{\boldsymbol{\alpha }} + {\mathit{\boldsymbol{K}}_2} \cdot \Delta \mathit{\boldsymbol{a}} + {\mathit{\boldsymbol{K}}_3} \cdot \Delta \mathit{\boldsymbol{d + }}{\mathit{\boldsymbol{K}}_4} \cdot \Delta \mathit{\boldsymbol{\theta }}} \right\|_2} $ | (6) |
其中符号‖·‖2为向量的2范数.由式(4)~式(6) 可知,给定D-H参数的名义值,系数矩阵Kj(j=1, 2, 3, 4) 成为确定值,机械臂的运动精度只与随机误差Δα、Δa、Δd以及Δθ相关.
1.2 机械臂运动轨迹可靠性建模设机械臂的微小随机误差向量表示为X=[x1, x2, x3, x4]=[Δα, Δa, Δd, Δθ],运动误差阈值为r0,根据应力强度干涉理论,运动轨迹功能函数为
| $ g\left( {\mathit{\boldsymbol{X}},\mathit{\boldsymbol{\theta }}\left( t \right)} \right) = {r_0} - r\left( {\mathit{\boldsymbol{X}},\mathit{\boldsymbol{\theta }}\left( t \right)} \right) $ | (7) |
其中:t为时间变量,r(X, θ(t))为实际运动误差.
对于固定的时刻ti,g(X, θ(t))退化为某个轨迹点处的功能函数gi(X, θ(ti)):
| $ \begin{array}{*{20}{c}} {{g_i}\left( {\mathit{\boldsymbol{X}},\mathit{\boldsymbol{\theta }}\left( {{t_i}} \right)} \right) = {r_0} - {r_i}\left( {\mathit{\boldsymbol{X}},\mathit{\boldsymbol{\theta }}\left( {{t_i}} \right)} \right) = }\\ {{r_0} - {{\left\| {{\mathit{\boldsymbol{K}}_1}{\mathit{\boldsymbol{x}}_1} + {\mathit{\boldsymbol{K}}_2}{\mathit{\boldsymbol{x}}_2} + {\mathit{\boldsymbol{K}}_3}{\mathit{\boldsymbol{x}}_3} + {\mathit{\boldsymbol{K}}_4}{\mathit{\boldsymbol{x}}_4}} \right\|}_2}} \end{array} $ | (8) |
其中ri(X, θ(ti))为时刻ti的实际运动误差.
机械臂在任务周期[0, T0]内任意时刻ti的安全域是一个以阈值r0为半径,末端期望位置坐标为球心的球域.当机械臂末端的实际位置处于球域以内时,运动可靠,反之则不可靠.机械臂运动轨迹可靠度,即末端实际位置位于球域内的概率可以表示为
| $ {R_{\rm{t}}} = \Pr \left\{ {g\left( {\mathit{\boldsymbol{X}},\mathit{\boldsymbol{\theta }}\left( t \right)} \right) > 0,t \in \left[ {0,{T_0}} \right]} \right\} $ | (9) |
由于复杂的多维积分计算,无法通过式(9) 求解运动轨迹可靠度.设[0, T0]内机械臂末端误差达到最大时所对应的时间为tmax(称为最大值时间),根据等效极值思想,若误差最大值r(tmax)≤r0,运动可靠,反之不可靠,以此将运动轨迹可靠性转换为轨迹点可靠性[9],然后用一次二阶矩法(FOSM, first order second moment)求解可靠度,快速、精确地确定tmax成为关键.提出使用自更新响应面法估算tmax,包含3个部分:粒子群优化算法(PSO, particle swarm optimization)计算tmax,基于Kriging模型构建关于tmax的响应面,建立自更新机制提升响应面精度.
1) PSO计算tmax
将随机向量样本Xi代入式(7) 的功能函数中:
| $ g\left( {{\mathit{\boldsymbol{X}}_i},\mathit{\boldsymbol{\theta }}\left( t \right)} \right) = {r_0} - r\left( {{\mathit{\boldsymbol{X}}_i},\mathit{\boldsymbol{\theta }}\left( t \right)} \right) $ | (10) |
功能函数转变为时间t的函数,记为g(t).通过求解g(t)在[0, T0]内的最小值(此时运动误差达到最大),可得到该样本的最大值时间tmax(Xi).
由于全局寻优能力以及较高的计算效率,使用PSO计算tmax. PSO算法中,每颗粒子代表一个潜在的优化解,最初的种群被随机赋予初始位置和初始速度,它们将沿着之前的最优位置加速更新,全局最优点表示为[10]
| $ v = wv + {c_1}{r_{{\rm{num1}}}}\left( {{p_{{\rm{best}}}} - z} \right) + {c_2}{r_{{\rm{num2}}}}\left( {{g_{{\rm{best}}}} - z} \right) $ | (11) |
| $ z = z + v $ | (12) |
其中:v为粒子速度,z为粒子当前位置,c1和c2为学习因子,rnum1和rnum2为[0, 1]之间随机数,w为加权系数,pbest为个体最优位置,gbest为全局最优位置,即所要求解的tmax.
2) 基于Kriging模型构建tmax的响应面[11]
设有m个样本(Xi, tmaxi),i=1, 2, …, m,tmaxi为对应于Xi的最大值时间.根据Kriging模型:
| $ {\mathit{\boldsymbol{t}}_{\max }}\left( \mathit{\boldsymbol{X}} \right) = {f^{\rm{T}}}\left( \mathit{\boldsymbol{X}} \right)\mathit{\boldsymbol{\gamma }} + Q\left( \mathit{\boldsymbol{X}} \right) $ | (13) |
其中:γ为回归系数,f(X)为回归函数,Q(X)为服从正态分布N(0, σ2)的偏差项,其协方差不为0,表示为
| $ C\left[ {Q\left( {{\mathit{\boldsymbol{X}}_i}} \right),Q\left( {{\mathit{\boldsymbol{X}}_j}} \right)} \right] = {\sigma ^2}R\left( {{\mathit{\boldsymbol{X}}_i},{\mathit{\boldsymbol{X}}_j}} \right),1 \le i,j \le m $ | (14) |
其中R(Xi, Xj)为高斯相关函数:
| $ R\left( {{\mathit{\boldsymbol{X}}_i},{\mathit{\boldsymbol{X}}_j}} \right) = \exp \left[ { - \sum\limits_{p = 1}^{{n_i}} {{\omega _p}{{\left( {\mathit{\boldsymbol{X}}_p^i - \mathit{\boldsymbol{X}}_p^j} \right)}^2}} } \right] $ | (15) |
其中:ωp(p=1, 2…, ni)为相关函数参数,ni为Xi中随机变量个数,Xpi与Xpj分别为Xi和Xj的第p个分量.
利用样本(Xi, tmaxi),i=1, 2, …, m,构造关于γ、σ2以及ω=[ω1, ω2, …, ωni]的对数似然函数L(γ, σ2, ω),如下式所示:
| $ \begin{array}{*{20}{c}} {L\left( {\mathit{\boldsymbol{\gamma }},{\sigma ^2},\mathit{\boldsymbol{\omega }}} \right) = - \frac{1}{2}\left[ {n\ln \left( {2{\rm{ \mathsf{ π} }}} \right) + n\ln {\sigma ^2} + \ln \left| \mathit{\boldsymbol{R}} \right| + } \right.}\\ {\left. {\frac{1}{{{\sigma ^2}}}{{\left( {{\mathit{\boldsymbol{t}}_{\max }} - \mathit{\boldsymbol{F\gamma }}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}\left( {{\mathit{\boldsymbol{t}}_{\max }} - \mathit{\boldsymbol{F\gamma }}} \right)} \right]} \end{array} $ | (16) |
其中:R为相关矩阵,tmax=[tmax1, tmax2, …tmaxm]T,F=[f(X1), f(X2), …, f(Xm)]T,R的表达式为
| $ \mathit{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} 1&{R\left( {{\mathit{\boldsymbol{X}}_1},{\mathit{\boldsymbol{X}}_2}} \right)}& \cdots &{R\left( {{\mathit{\boldsymbol{X}}_1},{\mathit{\boldsymbol{X}}_m}} \right)}\\ {R\left( {{\mathit{\boldsymbol{X}}_2},{\mathit{\boldsymbol{X}}_1}} \right)}&1& \cdots &{R\left( {{\mathit{\boldsymbol{X}}_2},{\mathit{\boldsymbol{X}}_m}} \right)}\\ \vdots&\vdots&\ddots&\vdots \\ {R\left( {{\mathit{\boldsymbol{X}}_m},{\mathit{\boldsymbol{X}}_1}} \right)}&{R\left( {{\mathit{\boldsymbol{X}}_m},{\mathit{\boldsymbol{X}}_2}} \right)}& \cdots &1 \end{array}} \right] $ | (17) |
将式(16) 分别对γ和σ2求导,可以得到两者的极大似然估计:
| $ {\mathit{\boldsymbol{\gamma }}^ * } = {\left( {{\mathit{\boldsymbol{F}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}\mathit{\boldsymbol{F}}} \right)^{ - 1}}\left( {{\mathit{\boldsymbol{F}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}{\mathit{\boldsymbol{t}}_{\max }}} \right) $ | (18) |
| $ {\sigma ^{2 * }} = \frac{{{{\left( {{\mathit{\boldsymbol{t}}_{\max }} - \mathit{\boldsymbol{F}}{\mathit{\boldsymbol{\gamma }}^ * }} \right)}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}\left( {{\mathit{\boldsymbol{t}}_{\max }} - \mathit{\boldsymbol{F}}{\mathit{\boldsymbol{\gamma }}^ * }} \right)}}{m} $ | (19) |
在获得γ*和σ2*之后,为求解相关函数参数ω,可转换为无约束最优化问题:
| $ \left. \begin{array}{l} 变量\;\mathit{\boldsymbol{\omega }}\\ 目标函数 - \frac{1}{2}\left( {n\ln \left( {{\sigma ^2}} \right) + \ln \left| \mathit{\boldsymbol{R}} \right|} \right) \to \max \end{array} \right\} $ | (20) |
在求得ω之后,最大值时间的预估值tmax*可以表示为
| $ t_{\max }^ * \left( \mathit{\boldsymbol{X}} \right) = {\mathit{\boldsymbol{\gamma }}^ * }{f^{\rm{T}}}\left( \mathit{\boldsymbol{X}} \right) + {\mathit{\boldsymbol{r}}^{\rm{T}}}\left( \mathit{\boldsymbol{X}} \right){\mathit{\boldsymbol{R}}^{ - 1}}\left( {{\mathit{\boldsymbol{t}}_{\max }} - \mathit{\boldsymbol{F}}{\mathit{\boldsymbol{\gamma }}^ * }} \right) $ | (21) |
其中r(X)=[R(X, X1), R(X, X2), …R(X, Xm)]T.
3) 建立自更新机制提升响应面精度
响应面的近似精度决定了可靠性分析结果的精确性,通过响应面自更新机制,当对新的样本输入的最大值时间估计不准确时,能够基于该样本自动进行更新.
Kriging响应面可提供最大值时间预估值的相对均方预估误差(RMSPE, relative mean square predicted error),RMSPE反映了Kriging响应面预估精度的分布趋势,以此作为更新响应面的依据,可有效提高响应面的近似精度. RMSPE的数学表达式为[12]
| $ \xi \left( \mathit{\boldsymbol{X}} \right) = \frac{{{\sigma ^{2 * }}\left[ {1 - {\mathit{\boldsymbol{r}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}\mathit{\boldsymbol{r}} + \frac{{{{\left( {1 - {\mathit{\boldsymbol{r}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}\mathit{\boldsymbol{r}}} \right)}^2}}}{{{{\bf{1}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}{\bf{1}}}}} \right]}}{{{\mathit{\boldsymbol{\gamma }}^ * }}} $ | (22) |
其中符号1为元素全为1的列向量.
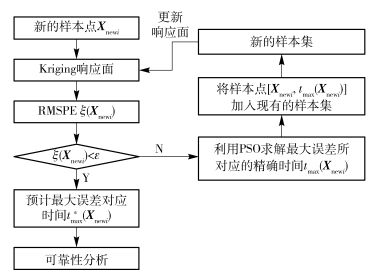
机械臂运动轨迹可靠性分析过程中,在利用Kriging响应面预估新的样本输入的最大值时间时,需事先依据式(22) 验证预估精度.若ξ(X)<ε(ε为精度阈值,可在10-2~10-3之间进行选择),表明Kriging响应面的近似精度满足要求,由式(21) 预估的最大值时间满足要求,无须更新响应面,可继续进行可靠性分析;否则需要利用PSO算法求解该样本点所对应的最大值时间的精确值,并将数据加入响应面的更新过程中,以提高其近似精度.自更新机制的流程图如图 2中所示.
|
图 2 响应面自更新机制流程图 |
步骤1 根据随机向量的概率分布,抽取m个初始样本X1, X2, …, Xm;
步骤2 利用PSO求解m个初始样本所对应的最大值时间集tmax=[tmax1, tmax2, …tmaxm]T;
步骤3 利用(Xi, tmaxi), i=1, 2, …, m构建Kriging响应面;
步骤4 将样本XRi代入式(21),得到最大值时间的预估值tmax*(XRi);
步骤5 再将样本XRi代入式(22),得到响应面的ξ(XRi);
步骤6 若ξ(XRi)>ε,响应面近似精度不满足要求,返回步骤2,利用PSO求解XRi所对应最大值时间的精确值tmax(XRi),然后继续步骤3,将[XRi, tmax(XRi)]添加到现有的样本集中,重新构造Kriging响应面;
步骤7 将tmax(XRi)代入式(8) 中,在XRi处利用FOSM进行可靠性分析;
步骤8 若ξ(XRi)<ε,响应面近似精度满足要求,直接将最大值时间的预估值tmax*(XRi)代入式(8) 中,在XRi处利用FOSM进行可靠性分析.
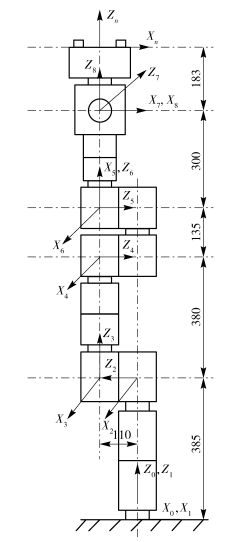
3 案例分析 3.1 机械臂运动学模型以一个八自由度的机械臂为对象,依据自更新响应面法进行运动轨迹可靠性分析.机械臂的关节坐标系定义如图 3所示,D-H参数如表 1所示.
|
图 3 八自由度机械臂关节坐标系 |
|
|
表 1 机械臂D-H参数表 |
机械臂末端的目标位置坐标设置为[-0.177 5 m, -0.067 5 m, 1.343 4 m],初始构型设置为[30°, 36°, -30°, 36°, -30°, 0°, 30°, 0°],任务周期为[0, 2 s],各关节在任务起始和结束时的速度为0.
机械臂的随机误差向量的概率分布如表 2所示,设置运动误差阈值r0=7.5 mm.每个随机向量抽取20个样本,根据自更新响应面法,运动轨迹可靠度Rt=0.905,计算耗时约40 s.计算机平台配置为:2.93 GHz的Intel Core2 Duo CPU E7500,2 GB运行内存,32位Win7操作系统.
|
|
表 2 机械臂随机向量概率分布 |
运动误差阈值r0分别取值6、6.5、7、7.5、8、8.5和9 mm. MCM中,样本数NMC=5 000;响应面法中(无自更新功能),每个随机向量抽取20个样本用于构造响应面;自更新响应面法中,每个随机向量抽取20个样本用于构造初始响应面.
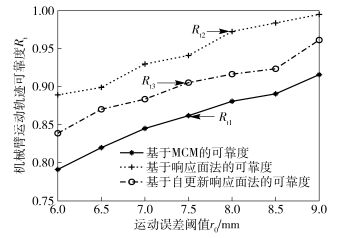
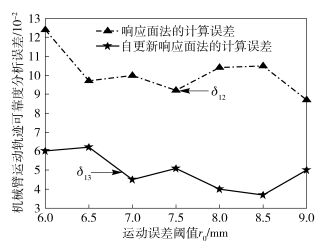
上述3种方法的分析结果如表 3~图 5所示. Rt1和T1分别为MCM的可靠度值和计算时间,Rt2和T2分别为响应面法的可靠度值和计算时间,Rt3和T3分别为自更新响应面法的可靠度值和计算时间,δ12和δ13分别表示响应面法和自更新响应面法的计算误差(以MCM结果为基准).
|
图 4 机械臂运动轨迹可靠度曲线 |
|
图 5 机械臂运动轨迹可靠度分析误差曲线 |
|
|
表 3 机械臂运动轨迹可靠性分析结果对比 |
根据上述可靠性仿真分析可以得出:
1) 对比MCM,响应面法的计算时间只是前者的6%左右,但该法计算误差较大,约为10%,计算精确性明显不足,反映出响应面的近似精度较差;
2) 对比响应面法,一方面,自更新响应面法的结果更加精确,计算误差基本在4.5%左右,比前者提高约1倍;另一方面,自更新响应面法的计算时间增加约60%~80%,但只是MCM的10%左右,新样本点的加入提高了响应面的近似精度,更新响应面却降低了计算效率.不过总体而言,自更新响应面法在计算效率与精确性之间取得了平衡.
4 结束语1) 针对机械臂运动轨迹可靠性分析的计算效率与精确性难题,提出了自更新响应面法,介绍了方法的基本原理,给出了详细的分析流程;
2) 可靠性分析结果表明:较之响应面法,自更新响应面法的计算精确性提高了约1倍,更接近MCM的计算结果,同时保持着较高的计算效率,在计算效率与精确性之间取得了平衡.该方法可推广应用于其他机构,有着较大的工程实用价值.
| [1] |
褚明, 贾庆轩, 孙汉旭, 等. 空间柔性操作臂的动力学/控制耦合特性研究[J]. 北京邮电大学学报, 2008, 31(3): 98–102.
Chu Ming, Jia Qingxuan, Sun Hanxu, et al. Coupling of the dynamics and control of the space flexible manipulative arm[J]. Journal of Beijing University of Posts and Telecommunications, 2008, 31(3): 98–102. |
| [2] | Rao S S, Bhatti P K. Probabilistic approach to manipulator kinematics and dynamics[J]. Reliability Engineering & System Safety, 2001, 72(1): 47–58. |
| [3] | Zhang Junfu, Du Xiaoping. Time-dependent reliability analysis for function generator mechanisms[J]. Journal of Mechnical Design, 2011, 133(3): 586–599. |
| [4] | Gao Zhenbang, Zhang Jianguo, Peng Wensheng, et al. Fuzzy time-dependent reliability modeling and analysis method for mechanisms based on strength degradation[C]//2014 Annual Reliability and Maintainability Symposium. Colorado:IEEE Press, 2014:1-7. |
| [5] | Li Jie, Chen Jianbing, Fan Wenliang. The equivalent extreme-value event and evaluation of the structural system reliability[J]. Structural Safety, 2007, 29(2): 112–131. doi: 10.1016/j.strusafe.2006.03.002 |
| [6] |
费成巍, 白广忱. 基于DCRSM的HPT叶尖径向运行间隙可靠性分析[J]. 航空学报, 2013, 34(9): 2141–2149.
Fei Chengwei, Bai Guangchen. Reliability analysis for HPT blade-tip radial running clearance based on DCRSM[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(9): 2141–2149. |
| [7] |
贾庆轩, 褚明, 孙汉旭, 等. 9-DOF超冗余机器人轨迹规划优化算法[J]. 北京邮电大学学报, 2008, 31(2): 20–25.
Jia Qingxuan, Chu Ming, Sun Hanxu, et al. Research on the optimal algorithm for trajectory planning of a 9-DOF hyper-redundant robot[J]. Journal of Beijing University of Posts and Telecommunications, 2008, 31(2): 20–25. |
| [8] |
陈钢, 贾庆轩, 李彤, 等. 机器人运动学参数递推标定方法[J]. 北京邮电大学学报, 2013, 36(2): 28–32.
Chen Gang, Jia Qingxuan, Li Tong, et al. Recursive calibrations for robot kinematics parameters[J]. Journal of Beijing University of Posts and Telecommunications, 2013, 36(2): 28–32. |
| [9] | Li Tong, Jia Qingxuan, Chen Gang, et al. Motion reliability modeling and evaluation for manipulator path planning task[J]. Mathematical Problems in Engineering, 2015: 1–13. |
| [10] |
徐俊杰, 忻展红. 基于两阶段策略的粒子群优化[J]. 北京邮电大学学报, 2007, 30(1): 136–139.
Xu Junjie, Xin Zhanhong. Particle swarm optimization based on a two-stage strategy[J]. Journal of Beijing University of Posts and Telecommunications, 2007, 30(1): 136–139. |
| [11] |
刘瞻, 张建国, 王灿灿, 等. 基于优化Kriging模型和重要抽样法的结构可靠度混合算法[J]. 航空学报, 2013, 34(6): 1347–1355.
Liu Zhan, Zhang Jianguo, Wang Cancan, et al. Hybrid algorithm of structural reliability based on optimal Kriging model and importance sampling[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(6): 1347–1355. |
| [12] | 陈小前, 姚雯, 欧阳琦. 飞行器不确定性多学科设计优化理论与应用[M]. 北京: 科学出版社, 2013: 192-193. |


