2. 北京邮电大学 信息与通信工程学院, 北京 100022
提出了一种基于删余的多天线协作频谱感知(C-MA-CSS),利用混合伽马分布推导了感知信道为复合衰落信道时C-MA-CSS的检测率、漏检率、虚警率和次系统容量的闭合表达式,并分析了它们与天线数的关系,给出了使次系统容量最大化的优化算法.仿真结果表明,相比非删余的CSS而言,一方面C-MA-CSS能够明显降低漏检率;另一方面,随着天线数的增多,次系统容量先增大后趋于平稳,采用优化算法可以在确保主用户受到足够保护的前提下,利用较少的天线数实现优化的次系统容量.
2. School of Information and Communication Engineering, Beijing University of Posts and Telecommunications, Beijing 100876, China
The censor-based cooperative spectrum sensing with multiple antennas (C-MA-CSS) was proposed, the closed-form expressions for the detection probability, miss-detection probability, the false-alarm probability and the secondary throughput were derived using the mixture Gamma distribution under the composite fading sensing channels. Then, the relationships between them and the number of antennas were analyzed, and the optimal algorithm for maximizing the secondary throughput was also given. Simulation results demonstrated that lower miss-detection probability can be achieved in C-MA-CSS compared to the non-censoring CSS. Besides, the secondary throughput monotonically increased rapidly first and slowly after. Meanwhile, optimal secondary throughput can be achieved with smaller number of antennas by the proposed algorithm while maintaining the target detection probability.
协作频谱感知技术(CSS, cooperative spectrum sensing)可以有效抵抗信道衰落,提高感知性能,其相关研究已经相对成熟[1-2].多天线频谱感知技术相比单天线协作频谱感知CSS技术可以进一步提高频谱感知性能,近年来备受关注[3-5]. Shi[3]研究了基于能量检测的多天线频谱感知性能,研究表明,多天线频谱感知相比单天线频谱感知能够获得更高的检测性能增益. Singh等[4]研究了感知信道为瑞利衰落且报告信道也存在衰落时,基于一种改进的能量检测器的多天线CSS性能的优化,研究表明使用最小化误码率准则可以实现在较低的信噪比范围内降低对主用户(PU, primary user)的干扰. Hammadi等[5]研究了感知信道为复合衰落信道且报告信道存在衰落时,基于多天线的CSS性能,分析了不同天线数下使得系统误码率最小时控制中心的融合方法.以上分析均验证了多天线协作的有效性,即利用多天线分集接收技术能够提高频谱检测性能.
而基于删余的CSS可以节约控制信道带宽,减少资源浪费.针对此问题,Rago等[6]研究了理想信道下分布式检测系统中的删余传感器性能;Sun等[7]研究了认知无线网络中带宽受限时的CSS性能,通过删余方式只将可靠的二进制判决结果发送给融合中心(FC, fusion center),减少通信带宽需求;李美玲等[8]研究了感知信道和报告信道均存在衰落时基于删余的CSS.
笔者考虑实际存在多径和阴影衰落等复杂的无线环境,进一步提出了基于删余的多天线CSS (C-MA-CSS, censor-based CSS with multiple antennas),推导了复合衰落信道下的检测率、漏检率、虚警率和次系统容量的闭合表达式, 并对检测率、漏检率、虚警率和次系统容量与天线数的关系进行了分析,在确保PU受到足够保护的前提下,给出了使次系统容量最大化的优化算法.分析和仿真结果表明, 相比非删余的CSS而言,一方面C-MA-CSS能够明显降低漏检率,随着天线数增多,漏检率越低;另一方面,天线数并非越多越好,随着天线数的增多,次系统容量先增大后趋于平稳,采用优化算法可以在确保PU受到足够保护的前提下利用较少的天线数实现优化的次系统容量.
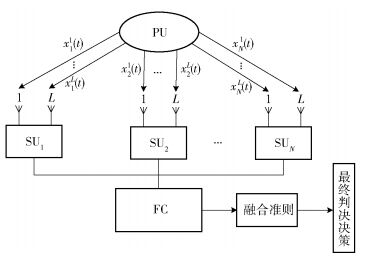
1 复合衰落信道下的C-MA-CSS模型图 1所示为C-MA-CSS模型,包含一个PU,N个次用户(SU, secondary user)和一个FC,每个SU配置L根天线,用SU ij表示第i个SU的第j根天线,i=1, 2…, N, j=1, 2…, L. C-MA-CSS过程如下:
|
图 1 C-MA-CSS模型 |
第1步 SU ij采用能量检测法独立地执行本地频谱感知,SUi采用平方律选择(SLS, square-law selection)分集合并技术对L根天线的二进制检测结果进行合并,并对PU信号的存在性做出统一判断.
第2步 SUi将合并的判决值通过报告信道发送到FC,考虑报告信道也存在衰落.为了节约控制信道带宽,SUi采用删余方式发送给FC,即只有SUi的判决值为“1”时才发送,否则不发送任何值.
第3步 FC采用“或”融合准则,即只要有一个SU检测到PU占用当前频带,那么FC就认定PU存在.
2 复合衰落信道下的C-MA-CSS性能 2.1 单用户单天线频谱感知当感知信道为复合衰落时,可以用广义混合伽马分布模型来近似表示其信噪比,用f(γij)表示感知信道信噪比的概率密度函数[9],则在复合衰落信道下SU ij的检测率Pdi, MGj、漏检率Pmi, MGj可计算如下:
| $ \begin{array}{*{20}{c}} {P_{{{\rm{d}}_i},{\rm{MG}}}^j = \int_0^\infty {{Q_u}\left( {\sqrt {2{\gamma _{ji}}} ,\sqrt \lambda } \right)f\left( {\gamma _i^j} \right){\rm{d}}\gamma _i^j} = }\\ {\int_0^\infty {{Q_u}\left( {\sqrt {2\gamma _i^j} ,\sqrt \lambda } \right)\sum\limits_{k = 1}^C {\frac{{{\alpha _k}}}{{\bar \gamma _i^j}}{{\left( {\frac{{\gamma _i^j}}{{\bar \gamma _i^j}}} \right)}^{{\beta _k} - 1}}{{\rm{e}}^{\left( { - \frac{{{\zeta _k}\gamma _i^j}}{{\bar \gamma _i^j}}} \right)}}} {\rm{d}}\gamma _i^j} = }\\ {\sum\limits_{l = 0}^\infty {\sum\limits_{k = 1}^C {\frac{{{\alpha _k}}}{{{{\left( {\bar \gamma _i^j} \right)}^{{\beta _k}}}}}\frac{{\mathit{\Gamma }\left( {u + l,\lambda /2} \right)}}{{l!\mathit{\Gamma }\left( {u + l} \right)}}} } \underbrace {\int_0^\infty {\frac{{{{\left( {\gamma _i^j} \right)}^{{\beta _k} + l - 1}}}}{{{{\rm{e}}^{\left( {1 + \frac{{{\zeta _k}}}{{\bar \gamma _i^j}}} \right)\gamma _i^j}}}}} }_R{\rm{d}}\gamma _i^j} \end{array} $ | (1) |
令R=
| $ \begin{array}{*{20}{c}} {R = }\\ {\int_0^\infty {\frac{{{{\rm{e}}^{ - \left( {1 + \frac{{{\zeta _k}}}{{\bar \gamma _i^j}}} \right)\gamma _i^j}}{{\left[ {\left( {1 + \frac{{{\zeta _k}}}{{\bar \gamma _i^j}}} \right)\gamma _i^j} \right]}^{{\beta _k} + l - 1}}}}{{{{\left( {1 + \frac{{{\zeta _k}}}{{\bar \gamma _i^j}}} \right)}^{{\beta _k} + l}}}}{\rm{d}}\left( {1 + \frac{{{\zeta _k}}}{{\bar \gamma _i^j}}} \right)\gamma _i^j} \overbrace = ^{t = \left( {1 + \frac{{{\zeta _k}}}{{\bar \gamma _i^j}}} \right)\gamma _i^j}}\\ {\int_0^\infty {\frac{{{{\rm{e}}^{ - t}}{t^{{\beta _k} + l - 1}}}}{{{{\left( {1 + \frac{{{\zeta _k}}}{{\bar \gamma _i^j}}} \right)}^{{\beta _k} + l}}}}{\rm{d}}t = \frac{{\mathit{\Gamma }\left( {{\beta _k} + l} \right)}}{{{{\left( {1 + \frac{{{\zeta _k}}}{{\bar \gamma _i^j}}} \right)}^{{\beta _k} + l}}}}} } \end{array} $ | (2) |
代入式(1) 可得到简化的无穷级数表达式:
| $ P_{{{\rm{d}}_i},{\rm{MG}}}^j = \sum\limits_{l = 0}^\infty {\sum\limits_{k = 1}^C {\frac{{{\alpha _k}}}{{{{\left( {\bar \gamma _i^j} \right)}^{{\beta _k}}}}}\frac{{\mathit{\Gamma }\left( {{\beta _k} + l} \right)\mathit{\Gamma }\left( {u + l,\lambda /2} \right)}}{{l!\mathit{\Gamma }\left( {u + l} \right){{\left( {1 + \frac{{{\zeta _k}}}{{\bar \gamma _i^j}}} \right)}^{{\beta _k} + l}}}}} } $ | (3) |
| $ P_{{{\rm{m}}_i},{\rm{MG}}}^j = 1 - P_{{{\rm{d}}_i},{\rm{MG}}}^j $ | (4) |
其中:γij为感知信道上的即时信噪比,γij为感知信道上的平均信噪比,βk和ζk为第k个元素内部衰落因子,且0≤αkΓ(βk)/ζkβk=1,λ为预定义的检测门限值,Γ(a, x)=
由于虚警率与接收信号即时信噪比γij无关,则复合衰落信道下SU ij的虚警率Pfi, MGj计算如下:
| $ P_{{{\rm{f}}_i},{\rm{MG}}}^j = \mathit{\Gamma }\left( {u,\lambda /2} \right)/\mathit{\Gamma }\left( u \right) $ | (5) |
考虑SUi每根天线独立执行频谱感知,各自感知信道独立同分布,则为方便分析,可省略上下标j和i. H0和H1分别表示PU未占用信道和占用信道两种状态.在SLS方案中,对于单个SU,选取所有L根天线中感知信道条件最好的支路,即
| $ {\gamma _{{\rm{SLS}}}} = \mathop {\max }\limits_{j = 1,2, \cdots ,L} \left( {{\gamma ^j}} \right) $ | (6) |
单个SU的平均虚警率Pf, SLS表达式为
| $ {{\bar P}_{{\rm{f}},{\rm{SLS}}}} = 1 - \Pr \left( {{\gamma _{{\rm{SLS}}}} < \lambda \left| {{H_0}} \right.} \right) $ | (7) |
将式(6) 代入式(7) 得到
| $ {{\bar P}_{{\rm{f}},{\rm{SLS}}}} = 1 - \Pr \left( {\max \left( {{\gamma _1},{\gamma _2}, \cdots ,{\gamma _L}} \right) < \lambda \left| {{H_0}} \right.} \right) $ | (8) |
即
| $ {{\bar P}_{{\rm{f}},{\rm{SLS}}}} = 1 - {\left[ {1 - {P_{{\rm{f,MG}}}}} \right]^L} $ | (9) |
同理,可以得到SLS方案下单个SU的平均检测率Pd, SLS及平均漏检率Pm, SLS表达式:
| $ {{\bar P}_{{\rm{d}},{\rm{SLS}}}} = 1 - {\left[ {1 - {P_{{\rm{d,MG}}}}} \right]^L} $ | (10) |
| $ {{\bar P}_{{\rm{m}},{\rm{SLS}}}} = 1 - {{\bar P}_{{\rm{d}},{\rm{SLS}}}} = {\left[ {1 - {P_{{\rm{d,MG}}}}} \right]^L} $ | (11) |
考虑SU与FC之间的报告信道也存在衰落,用错误传输概率Pe来衡量信道的优劣程度,由于单个SU以删余方式发送时,只发送本地判决值“1”,故单个SU采用删余方式将合并后的判决值经报告信道传输,到达FC之前单个SU的虚警率P′f, SLS, C、检测率P′d, SLS, C及漏检率P′m, SLS, C计算如下:
| $ {{P'}_{{\rm{f,SLS,C}}}} = \Pr \left\{ {H_1^{{\rm{SU}}}\left| {{H_0}} \right.} \right\}\left( {1 - {P_{\rm{e}}}} \right) = \left( {1 - {P_{\rm{e}}}} \right){{\bar P}_{{\rm{f}},{\rm{SLS}}}} $ | (12) |
| $ {{P'}_{{\rm{d,SLS,C}}}} = \Pr \left\{ {H_1^{{\rm{SU}}}\left| {{H_1}} \right.} \right\}\left( {1 - {P_{\rm{e}}}} \right) = \left( {1 - {P_{\rm{e}}}} \right){{\bar P}_{{\rm{d}},{\rm{SLS}}}} $ | (13) |
| $ {{P'}_{{\rm{m,SLS,C}}}} = \Pr \left\{ {H_0^{{\rm{SU}}}\left| {{H_1}} \right.} \right\}\left( {1 - {P_{\rm{e}}}} \right) = \left( {1 - {P_{\rm{e}}}} \right){{\bar P}_{{\rm{m}},{\rm{SLS}}}} $ | (14) |
单个SU将合并的判决值以删余方式通过报告信道发送给FC后,FC对特定频带上PU的存在与否做出最终的判决.用Δ表示C-MA-CSS方案中实际发送的本地决策值,且Δ≤N,根据贝叶斯原理,Δ可计算如下:
| $ \begin{array}{*{20}{c}} {\Delta = \left\lceil {N\left( {{P_0}\Pr \left( {H_1^{{\rm{SU}}}\left| {{H_0}} \right.} \right) + {P_1}\Pr \left( {H_1^{{\rm{SU}}}\left| {{H_1}} \right.} \right)} \right)} \right\rceil }\\ {\left\lceil {N\left( {{P_0}{{\bar P}_{{\rm{f}},{\rm{SLS}}}} + \left( {1 - {P_0}} \right){{\bar P}_{{\rm{d}},{\rm{SLS}}}}} \right)} \right\rceil } \end{array} $ | (15) |
其中:P0为信道未被PU占用的概率,P1为信道被PU占用的概率,且P0+P1=1;
FC采用“或”融合准则进行融合,则融合后的最终虚警率PF, C-MA-CSS、检测率PD, C-MA-CSS及漏检率PM, C-MA-CSS分别为
| $ {P_{{\rm{F,C}} - {\rm{MA}} - {\rm{CSS}}}} = \sum\limits_{i = 1}^\Delta {\left( \begin{array}{l} \Delta \\ i \end{array} \right){{\left( {{{P'}_{{\rm{f,SLS,C}}}}} \right)}^i}{{\left( {1 - {{P'}_{{\rm{f,SLS,C}}}}} \right)}^{\Delta - i}}} $ | (16) |
| $ {P_{{\rm{D,C}} - {\rm{MA}} - {\rm{CSS}}}} = \sum\limits_{i = 1}^\Delta {\left( \begin{array}{l} \Delta \\ i \end{array} \right){{\left( {{{P'}_{{\rm{d,SLS,C}}}}} \right)}^i}{{\left( {1 - {{P'}_{{\rm{d,SLS,C}}}}} \right)}^{\Delta - i}}} $ | (17) |
| $ {P_{{\rm{M,C}} - {\rm{MA}} - {\rm{CSS}}}} = \sum\limits_{i = 1}^\Delta {\left( \begin{array}{l} \Delta \\ i \end{array} \right){{\left( {{{P'}_{{\rm{m,SLS,C}}}}} \right)}^i}{{\left( {1 - {{P'}_{{\rm{m,SLS,C}}}}} \right)}^{\Delta - i}}} $ | (18) |
为了与C-MA-CSS进行对比,这里给出非删余MA-CSS方案的虚警率QF, MA-CSS、检测率Qd, MA-CSS及漏检率,分别计算如下:
| $ \begin{array}{*{20}{c}} {{P_{{\rm{F,MA}} - {\rm{CSS}}}} = \sum\limits_{i = 1}^N {\left( \begin{array}{l} N\\ i \end{array} \right){{\left( {{{P'}_{{\rm{f,SLS}}}}} \right)}^i} \cdot {{\left( {1 - {{P'}_{{\rm{f,SLS}}}}} \right)}^{N - i}}} = }\\ {\sum\limits_{i = 1}^N {\left( \begin{array}{l} N\\ i \end{array} \right){{\left[ {\left( {1 - {P_{\rm{e}}}} \right){{\bar P}_{{\rm{f,SLS}}}} + \left( {1 - {{\bar P}_{{\rm{f,SLS}}}}} \right){P_{\rm{e}}}} \right]}^i}} \times }\\ {{{\left( {1 - \left[ {\left( {1 - {P_{\rm{e}}}} \right){{\bar P}_{{\rm{f,SLS}}}} + \left( {1 - {{\bar P}_{{\rm{f,SLS}}}}} \right){P_{\rm{e}}}} \right]} \right)}^{N - i}} = }\\ {\sum\limits_{i = 1}^N {\left( \begin{array}{l} N\\ i \end{array} \right){{\left( {1 - {P_{\rm{e}}} + \left( {2{P_{\rm{e}}} - 1} \right){{\left[ {1 - {P_{{\rm{f}},{\rm{MG}}}}} \right]}^L}} \right)}^i}} \times }\\ {{{\left( {{P_{\rm{e}}} - \left( {2{P_{\rm{e}}} - 1} \right){{\left[ {1 - {P_{{\rm{f}},{\rm{MG}}}}} \right]}^L}} \right)}^{N - i}}} \end{array} $ | (19) |
| $ \begin{array}{*{20}{c}} {{P_{{\rm{D,MA}} - {\rm{CSS}}}} = }\\ {\sum\limits_{i = 1}^N {\left( \begin{array}{l} N\\ i \end{array} \right){{\left( {1 - {P_{\rm{e}}} + \left( {2{P_{\rm{e}}} - 1} \right){{\left[ {1 - {P_{{\rm{d}},{\rm{MG}}}}} \right]}^L}} \right)}^i} \times } }\\ {{{\left( {{P_{\rm{e}}} - \left( {2{P_{\rm{e}}} - 1} \right){{\left[ {1 - {P_{{\rm{d}},{\rm{MG}}}}} \right]}^L}} \right)}^{N - i}}} \end{array} $ | (20) |
| $ \begin{array}{*{20}{c}} {{P_{{\rm{M,MA}} - {\rm{CSS}}}} = }\\ {\sum\limits_{i = 1}^N {\left( \begin{array}{l} N\\ i \end{array} \right){{\left( {{P_{\rm{e}}} + \left( {1 - 2{P_{\rm{e}}}} \right){{\left[ {1 - {P_{{\rm{d}},{\rm{MG}}}}} \right]}^L}} \right)}^i} \times } }\\ {{{\left( {1 - {P_{\rm{e}}} + \left( {2{P_{\rm{e}}} - 1} \right){{\left[ {1 - {P_{{\rm{d}},{\rm{MG}}}}} \right]}^L}} \right)}^{N - i}}} \end{array} $ | (21) |
根据文献[8]的结论,得到C-MA-CSS数据传输阶段可获得的平均次系统容量为
| $ \begin{array}{*{20}{c}} {R\left( {\Delta ,L,\lambda } \right) = }\\ {\frac{{W - \Delta B}}{W}{C_0}{P_0}\left( {1 - {P_{{\rm{F,C}} - {\rm{MA}} - {\rm{CSS}}}}\left( {\Delta ,L,\lambda } \right)} \right) + }\\ {\frac{{W - \Delta B}}{W}{C_1}{P_1}\left( {1 - {P_{{\rm{D,C}} - {\rm{MA}} - {\rm{CSS}}}}\left( {\Delta ,L,\lambda } \right)} \right)} \end{array} $ | (22) |
其中:W为总的系统带宽,B为发送1 bit本地决策值占用的控制信道带宽,C0和C1分别为C-MA-CSS方案中SU在数据传输阶段PU不存在和存在两种场合可获得的次系统容量.
从实际应用的角度考虑,一方面要使得SU有更多的机会接入频谱,另一方面要避免通信过程中对PU的干扰,故对PU设定一个保护下限值PD, C-MA-CSS=0.9,此时,对可获得的次系统容量起主要作用的是等号右侧的第1项,则优化问题转化为
| $ \left. \begin{array}{l} \mathop {\max R }\limits_{\Delta ,L,\lambda } \left( {\Delta ,L,\lambda } \right) = \left( {1 - \Delta \alpha } \right)\left( {1 - {P_{{\rm{F,C}} - {\rm{MA}} - {\rm{CSS}}}}\left( {\Delta ,L,\lambda } \right)} \right)\\ {\rm{s}}{\rm{.}}\;{\rm{t}}{\rm{.}}\;\;\;\;\;\;{P_{{\rm{D,C}} - {\rm{MA}} - {\rm{CSS}}}}\left( {\Delta ,L,\lambda } \right) \ge {{\bar P}_{{\rm{D,C}} - {\rm{MA}} - {\rm{CSS}}}} \end{array} \right\} $ | (23) |
由式(23) 可知,次系统容量R受Δ、L、λ、PF, C-MA-CSS4个参数的影响,而PF, C-MA-CSS是Δ、L、λ的函数,故优化目标转化为确保通信过程中PU受到足够保护的条件下,使得数据传输阶段可获得的次系统容量最大化的优化组合(Δ, L, λ).根据文献[8]可以很容易得到,当天线数L一定时,如下结论成立.
结论1 虚警率PF, C-MA-CSS和检测率PD, C-MA-CSS均是感知分集阶数Δ的单调增函数;
结论2 虚警率PF, C-MA-CSS和检测率PD, C-MA-CSS是检测门限λ的递减函数.
接下来重点分析天线数L对次系统容量的影响.
结论3 当本地决策值数Δ、检测门限值λ一定时,次系统容量是天线数L的单调递减函数,即
| $ \frac{{\partial R\left( {\Delta ,L,\lambda } \right)}}{{\partial L}} < 0 $ | (24) |
证明 式(23) 对L求偏导可得
| $ \frac{{\partial R\left( {\Delta ,L,\lambda } \right)}}{{\partial L}} = - \left( {1 - \Delta \alpha } \right)\frac{{\partial {P_{{\rm{F,C}} - {\rm{MA}} - {\rm{CSS}}}}\left( {\Delta ,L,\lambda } \right)}}{{\partial L}} $ | (25) |
而
| $ \begin{array}{*{20}{c}} {\frac{{\partial {P_{{\rm{F,C}} - {\rm{MA}} - {\rm{CSS}}}}\left( {\Delta ,L,\lambda } \right)}}{{\partial L}} = }\\ {\frac{{\partial {P_{{\rm{F,C}} - {\rm{MA}} - {\rm{CSS}}}}\left( {\Delta ,L,\lambda } \right)}}{{{{P'}_{{\rm{f,SLS,C}}}}}} \cdot \frac{{\partial {{P'}_{{\rm{f,SLS,C}}}}}}{{\partial {{P'}_{{\rm{f,SLS}}}}}} \cdot \frac{{\partial {{\bar P}_{{\rm{f,SLS}}}}}}{{\partial L}}} \end{array} $ | (26) |
又
| $ \frac{{\partial {{\bar P}_{{\rm{f,SLS}}}}}}{{\partial L}} = - {\left[ {1 - {P_{{\rm{f}},{\rm{MG}}}}} \right]^L}\ln \left( {1 - {P_{{\rm{f}},{\rm{MG}}}}} \right) > 0 $ | (27) |
| $ \frac{{\partial {{P'}_{{\rm{f,SLS,C}}}}}}{{\partial {{\bar P}_{{\rm{f,SLS}}}}}} = 1 - {P_{\rm{e}}} > 0 $ | (28) |
| $ \begin{array}{*{20}{c}} {\frac{{\partial {P_{{\rm{F,C}} - {\rm{MA}} - {\rm{CSS}}}}\left( {\Delta ,L,\lambda } \right)}}{{{{P'}_{{\rm{f,SLS,C}}}}}} = }\\ {\Delta \left( \begin{array}{l} \Delta - 1\\ 0 \end{array} \right)\left( {{{P'}_{{\rm{f,SLS,C}}}}} \right)\Delta {{\left( {1 - {{P'}_{{\rm{f,SLS,C}}}}} \right)}^{\Delta - 1}} > 0} \end{array} $ | (29) |
将式(27)~式(29) 代入式(16) 可得
| $ \frac{{\partial {P_{{\rm{F,C}} - {\rm{MA}} - {\rm{CSS}}}}\left( {\Delta ,L,\lambda } \right)}}{{\partial L}} > 0 $ | (30) |
将式(30) 代入式(25) 可得
由上述可知,在天线数L、本地决策值Δ一定时,次系统容量是检测门限值λ的单调递增函数,而在天线数L、检测门限值一定时,Δ为次系统容量的单调递减函数,故需要折中分析(Δ, L, λ),以最大限度地保护PU通信不受干扰的同时最大化次系统容量.
3.2 算法设计优化的目标是为了找到使得次系统容量最大化的最佳(Δ, L, λ)组合,故优化算法设计如下:
1) 求参与协作的SU数N对应的最优检测门限值λNopt.由式(15) 可知,Δ为协作用户数N的函数,故:
① 通过式(15) 求C-MA-CSS方案中实际发送的本地决策值Δ,代入式(17),并得到与n维向量λn={λ1, λ2, , …, λn}中所有检测门限值相对应的目标检测率,对应的向量表示形式为PD, C-MA-CSS=(PD, C-MA-CSS(λ1), PD, C-MA-CSS(λ2), …, PD, C-MA-CSS(λn)}.
② 令Φ=PD, C-MA-CSS-δZ=(
③ 定义精度ε=10-4,并令i=1,j=1.
④ 如果|
2) 求出最优检测门限值时相对应的单个SU的本地虚警率Pf, SLSopt.
3) 利用2) 步的结果,根据式(16) 计算出最优门限值λNopt时相应的总虚警率PF, C-MA-CSSopt(λNopt).
利用第3) 步的结果,由式(23) 计算优化的次系统容量RC-MA-CSSopt(λNopt).
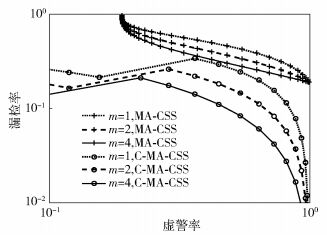
4 仿真结果及分析式(3) 中参数取C=2. 图 2所示为感知信道为Nak/lognormal复合衰落信道下衰落系数m取不同值时C-MA-CSS及MA-CSS方案的性能比较,横纵坐标分别为总的虚警率和漏检率.仿真中取L=1,N=2,u=5,ζ=0.5 dB,γ=10 dB,α=0.1,Pe=0.1,P0=0.5.由图 2可以看到,与MA-CSS方案相比,C-MA-CSS方案能够明显降低漏检率,抵抗衰落带来的影响,提高频谱检测性能.其中检测性能的好坏与衰落参数m的选取有关,相同虚警率下,随着m的增大,漏检率越小,SU对PU信号的检测越准确.
|
图 2 Nak/lognormal复合衰落下, m取不同值时的C-MA-CSS与MA-CSS性能比较 |
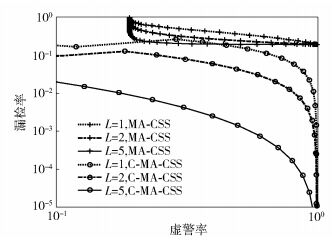
图 3所示为Nak/lognormal复合衰落信道下,m=2时,不同L下C-MA-CSS与MA-CSS性能比较.仿真中取N=2,u=5,ζ=0.5 dB,γ=10 dB,α=0.1,Pe=0.1,P0=0.5.从图 3可以看到:① 采用SLS分集接收后的检测性能明显高于未采用分集接收时的性能,随着天线数的增多,C-MA-CSS和MA-CSS方案的漏检率均降低,且相同虚警率、相同天线时,C-MA-CSS方案的漏检率明显低于MA-CSS方案;② C-MA-CSS方案不仅可以解决MA-CSS方案存在的虚警界问题,且随着天线数的增加,C-MA-CSS方案的漏检率较MA-CSS方案降低的更为明显.
|
图 3 Nak/lognormal复合衰落下,m=2时不同L下的C-MA-CSS与MA-CSS性能比较 |
图 4为不同天线数及衰落信道下C-MA-CSS方案中,检测率及次系统容量与检测门限的关系,N=2,u=5,ζ=0.5 dB,γ=10 dB,α=0.1,Pe=0.1,P0=0.5.从图 4中可以看到:① 在相同衰落条件下,SU数、检测门限值一定的情况下,检测率随着天线数L的增大而增大,而次系统容量随着天线数的增加而降低,与理论分析一致;② 不同衰落信道下,天线数L、检测门限值一定时,Weibull分布的检测率更高.

|
图 4 不同天线数及衰落信道下C-MA-CSS性能 |
图 5所示为不同衰落下采用优化算法后C-MA-CSS方案的次系统容量随天线数L的变化,N=2,u=5,ζ=0.5 dB,γ=10 dB,α=0.1,Pe=0.1,P0=0.5.从图 5中可以看出:① 以瑞利对数(RL, Rayleigh/lognormal)复合衰落,N=2,L=2为例分析,采用优化算法后次系统容量值为0.6,由图 4(a)可以看出满足最低保护下限PD, C-MA-CSS=0.9的条件下,检测门限值为17,再由图 4(b)可以得到次系统容量为0.6,两者所得值一样,故所提出的优化算法是合理的. ② 随着天线数的增大,次系统容量先增大后趋于平稳;③ 当N、L一定时,RL复合衰落下SU可获得的次系统容量明显低于Nakagam-m对数(NL, Nakagam-m/lognormal)复合衰落和Weibull多径衰落,当L=2时尤为明显,为了实现相同次系统容量,复合衰落下所需要的天线数较多.

|
图 5 优化后C-MA-CSS次系统容量随L的变化情况 |
笔者研究了感知信道为复合衰落信道且报告信道存在衰落时的C-MA-CSS性能,推导了复合衰落信道下的检测率、漏检率、虚警率和次系统容量的闭合表达式,分析了系统总的检测率、漏检率、虚警率和次系统容量与天线数之间的关系,设计了使得次系统容量最大化的优化算法.仿真结果表明,C-MA-CSS方案不仅可以解决MA-CSS方案存在的虚警界问题,相比MA-CSS方案能够明显降低漏检率,且随着天线数L增大,漏检率降低的更为明显,最大限度地克服了复合多径阴影衰落带来的影响,实现了对PU信号的更为准确的检测.同时, 所提优化算法在确保PU受到足够保护的条件下,实现了利用较少的天线数获得优化的次系统容量.
| [1] | Yang Guosheng, Wang Jun, Luo Jun, et al. Cooperative spectrum sensing in heterogeneous cognitive radio networks based on normalized energy detection[J]. IEEE Transactions on Vehicular Technology, 2016, 65(3): 1452–1463. doi: 10.1109/TVT.2015.2413787 |
| [2] | Li Meiling, Yuan Chaowei, Li Lin, et al. Analysis of secondary throughput and optimization in cooperative spectrum sensing[J]. The Journal of China Universities of Posts and Telecommunications, 2011, 18(4): 39–44. doi: 10.1016/S1005-8885(10)60081-7 |
| [3] | Shi Qinghua. On the performance of energy detection for spectrum sensing in cognitive radio over Nakagami-Lognormal composite channels[C]//International Conference on Signal and Information Processing. Beijing, China:[s.n.] 2013:566-569. |
| [4] | Singh A, Bhatnagar M, Mallik R. Cooperative spectrum sensing in multiple antenna based cognitive radio network using an improved energy detector[J]. IEEE Communications Letters, 2012, 16(1): 64–66. doi: 10.1109/LCOMM.2011.103111.111884 |
| [5] | Hammadi A A, Alhussein O, Sofotasios P, et al. Unified analysis of cooperative spectrum sensing over composite and generalized fading channels[J]. IEEE Transactions on Vehicular Technology, 2016, 65(9): 6949–6961. doi: 10.1109/TVT.2015.2487320 |
| [6] | Rago C, Willett P, Bar-shalom. Censoring sensors:a low communication-rate scheme for distributed detection[J]. IEEE Transactions on Aerospace and Electronic Systems, 1996, 32(2): 554–568. doi: 10.1109/7.489500 |
| [7] | Sun Chunhua, Zhang Wei, Letaief K B. Cooperative spectrum sensing for cognitive radios under bandwidth constraints[C]//IEEE Wireless Communications and Networking Conference. Kowloon, China:[s.n.], 2007:1-5. |
| [8] |
李美玲, 袁超伟, 李琳, 等. 使次系统容量最大化的协作频谱感知性能分析及优化[J]. 通信学报, 2011, 32(2): 53–60.
Li Meiling, Yuan Chaowei, Li Lin, et al. Performance analysis and optimization of cooperative spectrum sensing for maximizing secondary throughput[J]. Journal on Communications, 2011, 32(2): 53–60. |
| [9] | Atapattu S, Tellambura C, Jiang Hai. A mixture gamma distribution to model the SNR of wireless channels[J]. IEEE Transactions on Wireless Communications, 2011, 10(12): 4193–4203. doi: 10.1109/TWC.2011.111210.102115 |
| [10] | Selim B, Alhussein O. Karagiannidis G K, et al. Optimal cooperative spectrum sensing over composite fading channels[C]//IEEE International Conference Communications Workshops, London, United Kingdom:[s.n.], 2015:520-525. |


