为了提升大规模多用户多输入多输出系统的性能,对多用户选择方法进行了研究,提出了2种同时考虑用户信道质量和用户间干扰的多用户选择方法.通过将1 bit反馈法和最小化预编码向量相关性法结合,大大降低了用户选择的计算复杂度;基站端首先通过将所有用户组的预编码向量相关性与预定门限值比较,得到待选用户组的集合,然后选择待选用户组中信道增益和最大的一组用户服务,提升了系统的和容量.通过系统仿真验证了2种方法的有效性.
In multi-user massive (MIMO) wireless system, where the base station equipped with a large number of antennas simultaneously serves multiple users, user selection algorithms have become a rising concern. Two user selection algorithms, in which both channel quality and multi-user interference are taken in account, were proposed. The one is implemented by combining 1-bit feedback and minimizing the preceding vector correlation, it can effectively reduce the computation complexity; In the other algorithm, the list of users is got from potential users by comparing the preceding vector correlation with a threshold, then a set of users with the largest sum of the channel gain were selected, so the sum capacity is further improved. The performance and complexity of algorithms are analyzed.
大规模多输入多输出(MIMO, multiple-input multiple-output)技术作为下一代移动通信(5G)的候选关键技术之一,成为无线通信研究的热点[1].大规模MIMO系统若同时和多个用户通信可以更大程度地发掘多用户分集增益,因此大规模多用户MIMO(MU-MIMO, multi-user MIMO)是MIMO技术发展的方向.但是,由于同时服务多个用户,用户间的干扰会严重影响系统性能.研究显示,预编码技术结合多用户选择方法可以降低系统的多用户干扰,提升系统容量. Aziz等[2]指出基站端使用不同的预编码方法,适用的多用户选择方法也不同.而在大规模MIMO系统中,基于量化码本的预编码技术是一种可以适用于时分双工和频分双工系统的预编码方式.因此,设计针对量化预编码的多用户选择方法有很大的实用价值.
目前,已提出了大量的针对量化预编码的用户选择方法.经典的穷举法和轮询调度法分别提供了最大化系统容量和最优用户公平性.穷举法通过遍历所有用户组合,选取使系统容量最大的一组用户服务.该方法可以达到容量最大化,但是计算复杂度很高.轮询调度法不考虑各用户信道质量的差异,没有优先顺序地轮流服务各个用户.该方法充分保证了用户的公平程度,但是难以保证系统的容量.仅用1 bit来反馈信道信息的1 bit反馈法[3-4]大大降低了用户的反馈开销,同时考虑了用户的信道质量,但是并没有考虑用户间的干扰. Huang等[5]提出了每用户酉速率控制多用户选择方法,但是由于该算法苛刻的调度限制,使其在小区内用户数量较少时可能会出现调度失败的情况.张翔等[6]针对室内场景提出了一种综合考虑接收天线间的流间干扰和同一接收天线内的码间干扰的多用户调度方法,但是该方法只适用于室内的场景. Fang等[7]提出了一种基于最小化预编码向量相关性的用户选择方法,该方法大大降低了选择方法的复杂度,但是其仅考虑了多用户间的干扰而没有考虑用户的信道质量情况.
针对以上方法的缺点,笔者提出2种同时考虑用户信道质量和用户干扰的选择方法,这2种方法在系统同时调度用户数量较少时也可提升系统容量.
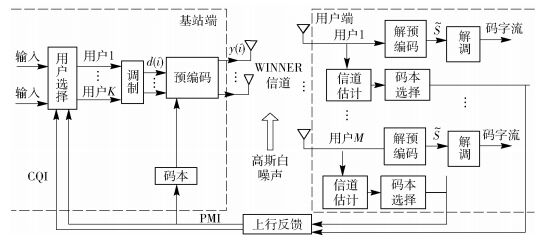
1 系统模型自适应调制大规模MU-MIMO系统下行链路基于量化码本的预编码系统模型如图 1所示.发送端配置Nt(Nt=NthNtv)根发射天线,水平维和垂直维天线数分别为Nth和Ntv.小区内有M个单天线用户,基站每次同时服务K个用户.
|
图 1 MU-MIMO系统下行链路预编码系统模型 |
在MU-MIMO系统中,第k个用户接收到的信号为
| ${\mathit{\boldsymbol{y}}_k} = {\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{W}}_k}{\mathit{\boldsymbol{x}}_k} + \sum\limits_{i = 1,i \ne k}^K {{\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{W}}_i}{\mathit{\boldsymbol{x}}_i} + {\mathit{\boldsymbol{n}}_k}} $ | (1) |
其中:Hk∈C1×Nt为第k个用户的信道矩阵;Wk∈CNt×1为第k个用户的最优预编码向量;xk为第k个用户的信号向量;nk为0均值的高斯白噪声,满足E(nnH)=σ2.
接收端除了将信息反馈给基站端外也会将信道估计矩阵H和预编码向量W反馈给解预编码模块进行处理,然后经过解调还原出码字流.当接收端使用匹配滤波器解预编码时,得到的解调信号为
| $\begin{array}{l} {{\hat x}_k} = \left( {{\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{W}}_k}} \right){y_k} = \\ {\left| {{\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{W}}_k}} \right|^2}{x_k} + \left( {{\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{W}}_k}} \right)\sum\limits_{i = 1,i \ne k}^K {{\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{W}}_i}{x_i} + \left( {{\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{W}}_k}} \right){n_k}} \end{array}$ | (2) |
假设每个用户的发射功率相同,可以得到用户k的接收信干噪比为
| $\begin{array}{l} {D_k} = \frac{{({P_t}/K)|{\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{W}}_k}{|^2}}}{{{\sigma ^2} + ({P_t}/K)\sum\limits_{i = 1,i \ne k}^K {|{\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{W}}_i}{|^2}} }} = \\ \quad \quad \frac{{{{\left\| {{\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{W}}_k}} \right\|}^2}}}{{K/\gamma + \sum\limits_{i = 1,i \ne k}^K {{{\left\| {{\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{W}}_i}} \right\|}^2}} }} \end{array}$ | (3) |
其中:Pt为基站总的发射功率,σ2为噪声功率,γ为信噪比.
根据式(3) 可以得到同时服务K个用户时系统的和容量为
| $\begin{array}{l} \quad \quad \quad R = \sum\limits_{k = 1}^K {{\rm{lb}}} \left( {1 + {D_k}} \right) = \\ \sum\limits_{k = 1}^K {{\rm{lb}}} \left( {1 + \frac{{{{\left\| {{\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{W}}_k}} \right\|}^2}}}{{K/\gamma + \sum\limits_{i = 1,i \ne k}^K {{{\left\| {{\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{W}}_i}} \right\|}^2}} }}} \right) \end{array}$ | (4) |
由式(3)、式(4) 可以看出,若想提升系统容量,就要增加信干噪比的分子减小分母,即选择信道质量较好和用户间干扰较小的用户.笔者提出了2种同时考虑用户干扰和用户信道质量的多用户选择方法,同时分析了2种方法的反馈开销和计算复杂度.
2.1 基于1 bit反馈的最小化预编码向量相关性法1 bit反馈法的核心思想:定义每个用户的等效信道增益‖HkWk‖为用户的信道质量,由式(4) 可以看出,在忽略多用户间干扰的情况下,服务信道增益大的用户可以有效地提升系统和容量.每个用户的信道质量与设置的一个门限进行比较,并反馈相应的信道质量信息,然后基站端在信道质量大于门限值的用户中随机选择用户进行服务.这样就可以减少一些待调度的用户,进而减少链路的反馈开销,也保证了能够达到一定系统的容量.
最小化预编码向量相关性法的核心思想:预编码矩阵的相关性可以代表用户信道的相关性,同时相关性较小的用户可以有效地降低用户间的干扰.
综合以上2种方法的优缺点可以提出同时考虑用户信道质量和用户干扰的基于1 bit反馈的最小化预编码向量相关性法.该方法的具体步骤如下.
第1步 用户端根据估计到的信道信息与反馈门限值α做比较,并反馈相应的信道质量信息Ik(见式(5))给基站.
| ${I_k} = \left\{ {\begin{array}{*{20}{c}} 1&{\left\| {{\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{W}}_k}} \right\| > \alpha }\\ 0&{\left\| {{\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{W}}_k}} \right\| < \alpha } \end{array}} \right.$ | (5) |
第2步 基站端根据收到的信道质量信息将用户分为待选择用户集合Ω1和不选择用户集合Ω2.反馈信息Ik为1的用户归为Ω1,反馈信息Ik为0的用户归为Ω2.
第3步 基站端在集合Ω1中选择预编码矩阵相关性最小的一组用户服务.
若集合Ω1中的用户数目N大于K,基站端计算Ω1中所有可能的用户组的预编码矩阵的相关性,并选择相关性最小的一组用户服务,即
| $\mathop {{\rm{min}}}\limits_{{S_i} \in {\mathit{\Omega }_1}} {\left\| {{\mathit{\boldsymbol{P}}^{\rm{H}}}_{({S_i})}{\mathit{\boldsymbol{P}}_{({S_i})}}} \right\|_1},i = 1,{\rm{ }}2, \cdots ,C_N^K$ | (6) |
其中:Si为集合Ω1中的一组用户,P(Si)为Si的预编码矩阵.
若集合Ω1中的用户数目N小于K,基站端在集合Ω2中随机选择(K-N)个用户加入集合Ω1,并为该组用户提供服务.
该方法最关键的问题是如何设置合适的反馈门限值.门限值越小,进入待选择用户集合的用户数目越多,能更大程度地消除多用户间的干扰.但是,此时基站端的计算复杂度增加,且一些信道质量不高的用户也会进入待选择用户集合,影响系统性能.
2.2 基于预编码向量相关性的最大范数法最大范数法的核心思想:等效信道的范数可以在一定程度上表示系统容量.计算待调度用户集合的范数可以降低多用户选择方法的计算复杂度,同时也保证了系统的容量.
综合最大范数法和最小化相关性法的优缺点,可以提出同时考虑用户信道质量和用户干扰的基于预编码矩阵相关性的最大范数法.该方法的步骤如下.
第1步 基站端根据用户反馈的预编码矩阵索引(PMI, precoding matrix index)计算所有可能用户组的预编码向量相关性,并将其与预定的相关性门限值β做比较,得到待选用户组的集合Ω3.即
| ${\mathit{\Omega }_3} = \{ {S_i}|{\left\| {{P^H}_{({S_i})}{P_{({S_i})}}} \right\|_1} < \beta ,{\rm{ }}i = 1,{\rm{ }}2,{\rm{ }} \cdots ,{\rm{ }}C_M^K\} $ | (7) |
第2步 基站端分别计算集合中所有待选用户组的等效信道增益的F范数的二次方和,并选择二次方和最大的一组用户服务.即
| $S = \mathop {\arg \;\max }\limits_{{S_i} \in {\mathit{\Omega }_3}} \left( {\begin{array}{*{20}{c}} {\left\| {\mathit{\boldsymbol{H}}_{{S_i}}^1\mathit{\boldsymbol{W}}_{{S_i}}^1} \right\|_F^2 + \left\| {\mathit{\boldsymbol{H}}_{{S_i}}^2\mathit{\boldsymbol{W}}_{{S_i}}^2} \right\|_F^2 + \cdots + }\\ {\left\| {\mathit{\boldsymbol{H}}_{{S_i}}^K\mathit{\boldsymbol{W}}_{{S_i}}^k} \right\|_F^2} \end{array}} \right)$ | (8) |
该方法的关键是如何选择合适的相关性门限值.设置的相关性门限值越大,满足门限值的用户组数目越大,系统容量越明显.但是,基站端的计算复杂度也增加的越多.同时,过大的门限值将限制用户干扰的消除程度.
3 仿真结果及分析仿真时采用的信道为WINNER 2信道[8],参数设置参考文献[7].信道的载波频率为2.6 GHz,信道带宽为10 MHz,场景选择为典型微城市小区非视距.小区是半径为500 m的圆形小区,基站位于小区中心,高度为32 m.基站端配置8×8的均匀平面天线阵列,天线间的距离为半波长.小区内随机出现10个用户,每个用户配置单个天线,每个用户高度设置为1 m.系统使用基于码本的预编码,使用的码本为旋转离散傅里叶变换(DFT,discrete Fourier transform)码本[9].
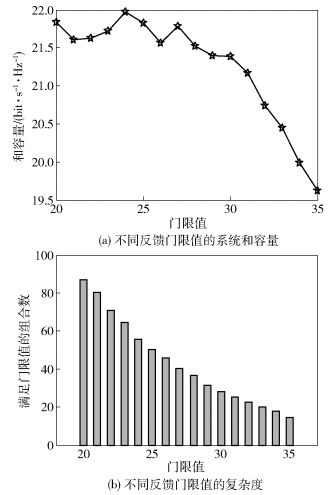
通过分析多用户选择方法的过程可以知道,门限值的设置会影响系统和容量性能和多用户选择方法的计算复杂度.如果门限值设置得过大,只有很少的用户进入到待选择用户集合,而大部分用户不能受到服务.尽管会在这部分用户中再挑选相互干扰较小的用户组合来服务,但是这些用户的多用户干扰如果很大的话就可能会影响最终的和容量性能.实验过程中基站同时服务4个用户,系统信噪比为20 dB时,图 2(a)和(b)分别显示了基于1 bit反馈的最小化预编码向量相关性法设置不同的反馈门限值时系统和容量和复杂度代价的比较.
|
图 2 不同反馈门限值性能比较 |
由图 2(a)可以看出,在门限值设置小于30时系统和容量并没有很大的波动,而当门限值大于30时系统和容量急剧下降.这是因为随着门限值的增加,能够进入待选用户集合的用户减少.进入待选用户集合的用户较少,无法获得干扰最小的一组用户,因此系统和容量会下降.同时,根据图 2(b)可以看出,随着门限值的增大,多用户选择方法的计算复杂度是逐渐降低的.如果不考虑系统和容量的下降,可以知道门限值越大越好.但是综合考虑系统和容量和计算复杂度,最佳门限值就是那个保证系统和容量不下降太明显,而计算复杂度又低的值.比较性能和复杂度可以得到在小区内有10个用户分布,基站同时服务4个用户时的最佳门限值为30,其他情况的最佳门限值可以通过相同的方法分析获得.
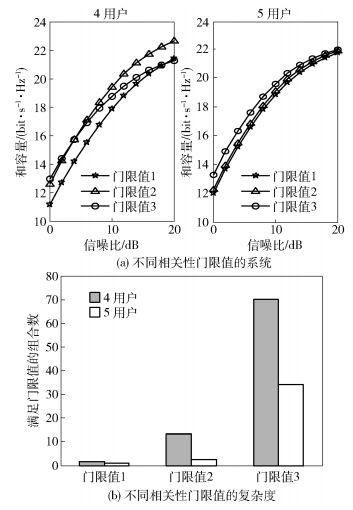
基于预编码向量相关性最大范数法的相关性门限值设置需要考虑系统性能和计算复杂度. 图 3(a)显示了系统分别为4和5个用户服务时设置不同相关性门限值所引起的系统和容量变化,图 3(b)显示了系统分别为4和5个用户服务时设置不同相关性门限值所需要付出的额外复杂度代价. 图 3中的门限值1为1+10-2、门限值2为1+10-1、门限值3为1+10-0.5.
|
图 3 不同相关性门限值性能比较 |
从图 3(a)中可以看出,对于同时为5个用户服务的系统来说,门限值设置为1+10-0.5时的系统和容量最大.虽然随着门限值的增大,满足门限值的用户组合数增加,但是对于5个用户能满足门限值的组合数并没有很多.对于同时服务4个用户的系统来说,门限值设置为1+10-1时的系统和容量最大.系统和容量并没有随着用户组合数的增大而增大的原因是,门限值的增大是削弱了用户间干扰消除的效果,而基站端是基于范数而不是容量来选择用户的,这样势必会降低系统的容量性能.
小区内同时服务的用户数也是多用户选择方法的关键参数之一.同时服务不同用户数目的多用户选择方法的性能比较如图 4所示.

|
图 4 不同用户数的系统和容量 |
由图 4所显示的结果可以看出,在同时调度4个用户时,所提出的2种方法性能都优于最小化预编码向量相关性法和1 bit反馈法.这是因为所提出的2种方法同时考虑了多用户干扰和用户信道质量,而原始的方法都只是从某一方面考虑的.由图 4所显示的结果可以看出,在同时调度5个用户时,所提出的基于预编码向量相关性的最大范数法性能优于传统的2种方法,但是基于1 bit反馈的最小化预编码向量相关性法性能劣于最小化预编码向量相关性的用户选择方法.这是因为随着同时调度的用户数目增加和信噪比的升高,多用户间的干扰成为影响系统性能的主要因素,最小化预编码向量相关性法可以更好地消除多用户间的干扰.基于1 bit反馈的最小化预编码向量相关性法由于首先考虑的是信道质量,因此会在一定程度上影响找到干扰最小的用户组.
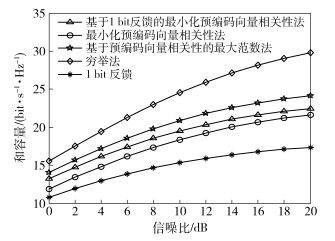
同时为4个用户服务时不同多用户选择方法随着信道信噪比变化的系统和容量如图 5所示.
|
图 5 系统和容量比较 |
由图 5所显示的结果可以看出,所提出的2种多用户选择方法的性能均优于最小化预编码向量相关性法和1 bit反馈法.但是与穷举法相比,所提出方法的性能较差,并且这种差距随着信道比的增加而变得更加明显.这是因为随着信噪比的增加,用户间的干扰成为影响多用户系统性能的主要因素,穷举法通过遍历所用可能的用户组合可以更加有效地降低多用户间的干扰.
4 反馈开销及复杂度分析相比于最小化预编码向量相关性法,基于1 bit反馈的最小化预编码向量相关性法增加了反馈开销,增加的反馈开销与小区内的用户数相关.每个用户在反馈的过程中需要反馈1 bit的用户信道质量信息,因此增加的反馈开销为Mbit.而基于1 bit反馈的最小化预编码向量相关性法相比最小化预编码向量相关性法,降低了基站端的计算复杂度.最小化预编码向量相关性法需要基站端计算F2=CMK组用户组合的预编码矩阵的相关性,并排序选择最小值.而基于1 bit反馈的最小化预编码向量相关性法只需要计算F1=CNK(N<M)组用户组合的预编码矩阵的相关性,并排序选择最小值.
相比于最小化预编码向量相关性法,基于预编码向量相关性的最大范数法增加了反馈开销和计算复杂度.每个用户在反馈的过程中需要反馈自己等效信道增益的F范数量化值,假设每个用户需要的反馈开销为Bbit,则增加的反馈开销为M×Bbit.基于预编码向量相关性的最大范数法中基站端需要计算待选用户组合的F范数二次方和,并比较其大小.假设待选用户组合数为D组,则基站端需要增加K×D次乘法,(K-1)×D次加法,并比较D个值的大小.
假设需要计算预编码矩阵相关性的多用户组合数为多用户选择算法的计算复杂度,所提出的基于1 bit反馈的最小化预编码向量相关性法与最小化预编码向量相关性法的计算复杂度比较如图 6所示.

|
图 6 计算复杂度比较 |
由图 6可以看出,最小化预编码向量相关性法的计算复杂度随着小区内用户数目的增加而极速增加,而所提出的方法很大程度上降低了计算复杂度.原因是通过将信道增益与门限值做比较,减少了作为备选用户的数目,低计算复杂度的优势随着小区内用户数目的增加而更加明显.
5 结束语针对基于码本的预编码系统的多用户选择问题,提出了2种同时考虑用户信道质量和用户干扰的多用户调度方法.仿真结果表明,基于1 bit反馈的最小化预编码向量相关性法提升了系统容量,同时可以有效地降低计算复杂度;基于预编码向量相关性的最大范数法可以有效地提升系统容量.
| [1] |
尤肖虎, 潘志文, 高西奇, 等. 5G移动通信发展趋势与若干关键技术[J]. 中国科学:信息科学, 2014, 44(5): 551–563.
You Xiaohu, Pan Zhiwen, Gao Xiqi, et al. 5G mobile communications and its promotion[J]. SCIENCE CHINA Information Sciences, 2014, 44(5): 551–563. |
| [2] | Aziz D, Mazhar M, Weber A. Impact of multi user selec-tion on the performance of transmit precoding in MU-MIMO cellular systems[C]//2013 IEEE Wireless Communications and Networking Conference (WCNC). Shanghai:[s. n.], 2013:3191-3196. |
| [3] | Floren F, Edfors O, Molin B A. The effect of feedback quantization on the throughput of amultiuser diversity scheme[C]//2003 IEEE Global Telecommunications Conference.[S. l.]:IEEE, 2003:497-501. |
| [4] | Sanayei S, Nosratinia A. Exploiting multiuser diversity with only 1-bit feedback[C]//2005 IEEE Wireless Communications and Networking Conference.[S. l.]:[s. n], 2005:978-983. |
| [5] | Huang Kaibin, Andrews J G, Heath R W. Performance of orthogonal beam-forming for SDMA with limited feedback[J]. IEEE Transactions on Vehicular Technology, 2009, 58(1): 152–164. doi: 10.1109/TVT.2008.925003 |
| [6] |
张翔, 李勇, 彭木根, 等. TD-HSUPA MU-MIMO室内调度及用户配对[J]. 北京邮电大学学报, 2012, 35(2): 64–67.
Zhang Xiang, Li Yong, Peng Mugen, et al. Indoor scheduling and user pairing for TD-HSUPA MU-MIMO system[J]. Journal of Beijing University of Posts and Telecommunications, 2012, 35(2): 64–67. |
| [7] | Fang Yan na, Su Xin, Zeng Jie. Effective user selection algorithm for quantized precoding in massive MIMO[C]//20138th International ICST Conference on Communications and Networking in China. Guilin:[s. n.], 2013:353-357. |
| [8] | Pekka K, Meinila J, Hentila L, et al. IST-4-027756_2007, winner Ⅱ D1. 1. 2 V1. 2 winner Ⅱ channel models[S].[S.l.]:Information Society Technologies, 2007:9-60. |
| [9] | Wu Xuewen, Jing Xiaorong, Liu Li. 3D MU-MIMO precoding method based on Khatri-Rao product[J]. Telecommunication Engineering, 2014, 54(11): 1510–1515. |


