2. 北京交通大学 软件学院, 北京 100044
特征融合方法是模式识别领域的一种重要方法.计算机视觉领域的图像识别问题作为一种特殊的模式分类问题,仍然存在很多挑战.特征融合方法能够综合利用多种图像特征,实现多特征的优势互补,获得更加鲁棒和准确的识别结果.笔者基于信息融合理论分析了特征融合方法的原理,介绍了特征融合方法的研究现状,讨论了特征融合与3类主流基础理论相结合的方法,其中基于贝叶斯理论的特征融合算法可以实现多特征的融合决策,基于稀疏表示理论的特征融合算法能够得到多特征的联合稀疏表示,基于深度学习理论的特征融合算法能够强化深度神经网络模型的特征学习过程.
2. School of Software Engineer, Beijing Jiaotong University, Beijing 100044, China
Feature fusion is an important method in pattern recognition. Image recognition problem in computer vision can be known as a special pattern classification problem, and it still have many challenges. To solve the problem, feature fusion method is able to use multi-feature of image, complement each other's advantages and get more robust and accurate results. Based on information fusion theory, analyze the theory of feature fusion and introduce the development of feature fusion methods. Besides, discuss three methods of feature fusion combining with other basic theories. Bayesian decision theory based feature fusion algorithm implements fusion decision of multi-feature. Sparse representation based feature fusion algorithm can get the joint sparse representation of multi-feature. Deep learning based feature fusion algorithm intensifies feature learning process of deep neural network model.
图像识别问题是计算机视觉领域要解决的基础问题,如果将图像看作一种模式,那么图像识别问题也是一种特殊的模式分类问题,包括早期的光学字符识别、生物特征识别中的人脸识别、指纹识别、虹膜识别,也包括场景识别、视频中的目标识别、动作识别等.基于传统的模式分类方法,这类问题已经得到一定程度的解决,例如支持向量机、人工神经网络、近邻法等方法,通过特征提取、分类器训练过程得到分类器,输出分类结果.但是,传统的模式分类方法通常基于人工设计的特征,经过特征提取算法得到原始图像的特征数据,例如颜色特征、SIFT特征、HOG特征、HOF特征、GIST特征等,而这些特征数据却存在类内方差较小而类间方差较大的问题.因为一种特征通常只对图像部分特性的变化较为敏感,而对其他特性的变化不敏感,所以,当两类图像的差异在某种特征敏感特性上的差异不大时,基于单一特征训练的分类器就无法输出正确的分类.除此之外,图像中复杂的背景噪声也会导致特征数据质量下降,既增加分类器训练的难度,又降低分类的准确性.
解决这种问题的一种思路就是使用特征融合方法,同时提取多种特征进行分类器训练,实现特征互补,降低单一特征固有缺陷的影响.特征融合方法的思想来源于早期的信息融合(information fusion)领域,它的数据主要来源于多种传感器,用于军事领域的多传感器融合.早期信息融合的基础理论主要包括模糊集、证据理论等,后来信息融合在民用领域得到了较快的发展,尤其是在生物安全认证方面[1],进行多生物特征的融合识别.目前在学术界被公认的信息融合层次划分为分类器级(决策级)、特征级和数据级,处理数据的维度和总量依次升高.在模式识别领域,受到计算机运算能力的限制,早期的研究主要集中在分类器级的融合算法,例如,Kittler等[2]提出的基于贝叶斯决策理论的分类器融合框架,为以后的研究奠定了良好的基础.近年来,随着人工智能技术的发展,特征融合成为研究热点,特别是在图像识别问题中得到了广泛的应用.
1 特征融合原理特征融合在信息融合中属于中间层次的融合,信息融合理论是特征融合的基础理论.信息融合是对多源异构数据进行综合处理,从而达到联合决策的目的.其实,人类对事物的认知过程就是对多源信息的融合过程[3],人们每时每刻都在通过视觉、听觉、触觉、嗅觉、味觉等多种感官接收各种各样的信息,这些信息转化成了神经脉冲信号传输到大脑皮层进行综合决策.实际应用中,由于多源数据的结构和含义不同,在处理时不能一概而论,必须经过融合算法处理.在计算机视频和模式识别领域,使用特征融合方法解决图像识别问题,就是基于信息融合思想,通过融合算法使用图像多角度、多层次的特征(图像的颜色、形状、梯度)、空间特征和时间特征、全局特征和局部特征等,来实现更智能的图像信息处理.
随着学术研究的推进,信息融合的数据来源更加多样,应用的领域也更加广泛,特别是CPU、GPU计算性能的显著提升,大规模分布式计算、并行计算模型进一步发展,人类能够对大数据进行快速处理,这使得信息融合的研究从分类器级推进到了特征级和数据级的层面.如果将图像识别问题看作模式分类问题,那么使用特征融合方法主要基于2个基本的经验性假设:1) 融合多特征通常比单一特征具有更好的分类性能;2) 进行融合的多种特征之间相关性较小.前者是应用该方法的出发点和基础思想,后者对于图像多特征的选择具有指导意义.应当从多个角度选择相关性尽量小的特征参与特征融合,才能发挥该方法的优点,实现特征互补.特征融合方法直接作用在特征上面,它的优点在于可以直接利用已有的特征提取算法提取特征,相对于重新设计特征和特征提取算法,其花费的代价更低.
模式分类问题的解决过程一般包括数据获取、预处理、特征提取、分类器设计与训练和分类决策等步骤,如图 1所示,信息融合的3个层次恰好可以与这个过程对应.特征保留了必要的、显著的信息,既降低原始数据的冗余性,减少数据噪声,又比分类器决策结果有更充分的数据信息,数据量和数据维度适中,因此在这个层次上进行融合是目前最优的选择.引入特征融合方法的模式分类问题可以表述为,定义模式空间Ω={ω1, ω2, …, ωc}和样本集合X,其中ωk表示一个模式类,X中每个元素Xj是一个样本的特征集合,其中j∈[1, P],P为样本总数;特征集合Xj={Xj1, Xj2, …, XjD}表示样本有D种特征,样本特征向量Xji={xj1i, xj2i, …, xijni}∈Xj,xjnii表示样本第种i特征的一个维度,ni是这种特征的维度,N=
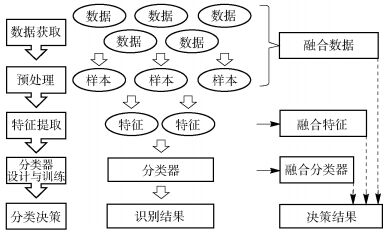
|
图 1 融合层次与模式分类 |
特征融合早期应用在生物特征识别方面,瑞士IDIAP研究所和格里菲斯大学的研究人员Sanderson和Pailwal[1]在2004年发布的研究报告中总结了信息融合在个体生物认证方面的理论和技术,并且将信息融合划分为先映射融合(pre-mapping fusion)和后映射融合(post-mapping fusion),即根据信息融合发生在分类器(classifier)处理之前还是之后来划分.通常文献中提到的数据级融合(data level fusion)和特征级融合(feature level fusion)属于前者,分值级融合(score level fusion)和分类器级融合(classifier level fusion)属于后者,分类级融合也被认为是决策级融合(decision level fusion).虽然在学术研究中,不同级别的融合概念早就被提出来,但是受到计算机处理能力的限制,直接进行特征级甚至数据级的信息融合往往不容易.因此,早期的研究主要集中于分值级融合和分类器级融合. Kittler[2]提出的基于贝叶斯决策理论的分类器融合框架,总结了乘法规则、加法规则、最大规则、最小规则、中位数规则、多数票规则等经典的融合规则,是分类器级融合良好的基础工作,也为特征融合奠定了基础. Kuncheva[4]在这个基础上进行了理论研究,对基于贝叶斯的融合方法的分类错误率进行了建模分析,论证了融合方法的优势.而Jain[5]在2005发表的论文中归纳总结了多模生物特征识别系统中各种分值规则化的方法,成为分值级融合的经典文献,受到研究人员的广泛关注,之后发展出了基于变换、基于分类器、基于概率密度的分值级融合等各个分支.在此基础上,Nandakumar等[6]使用高斯混合模型改进了原有的单纯基于高斯分布的分值级融合方法,重新定义了似然比融合规则(likelihood ration fusion rule),在人脸、指纹、虹膜、声音等生物特征识别中取得了良好的效果.随着学术研究的推进,特征融合的优势逐渐体现出来,Ma等[7]在线性融合模型的基础上分别提出了分类器级和特征级的线性依赖模型,通过增加依赖项来解决求解联合概率密度时独立同分布条件的限制问题,是对基于贝叶斯理论框架的融合方法的发展.与稀疏表示理论相结合,Shekhar等[8]提出基于联合稀疏表示的特征级融合方法,也应用于多模生物特征的识别中,通过优化一个正则的最小二乘问题求解多模生物特征的联合稀疏表示矩阵. Yan等[9]引入了稀疏的思想并结合特征融合方法,在原有的降秩回归模型(RRR, reduced-rank regression)基础上进行改进,提出了稀疏核降秩回归模型(SKRRR, sparse kernel reduced-rank regression),将人说话时的语音特征和面部表情特征的进行融合,实现双模的表情识别. Bai等[10]使用特征融合的方法解决图像检索中的重排序(re-ranking)问题,提出一种新的稀疏情景激活的图像特征. Zhang L等[11]提出半监督的多特征学习方法,使用全局标签一致分类器实现多特征的共享学习.视频作为增加了时序信息的图像数据,特征融合方法也被应用到解决基于视频的目标识别和动作识别问题中,应对视频数据本身所具有的复杂性.视频数据中图像的空间结构信息也通常被视为提高视频识别性能的有效信息,而SIFT、HOG、HOF等特征提取方法在提取图像特征之后,会丢失空间结构信息,Yu等[12]提出了一种基于局部能量特征的二元表示方法,能够保持原始图像的结构信息,进而提高视频识别的准确性. Demirkus等[13]通过与多特征融合的方法相结合,提出了一种层级式的时空概率图模型来提取二元的人脸特征,解决视频中的人脸识别问题. Hu等[14]在处理携带有景深信息的视频数据中,提出了一种联合学习模型,实现多通道异构特征的融合,解决动作识别问题.与融合思想相结合的融合深度学习方法也被应用在视频目标识别的任务中,Feichtenhofer等[15]在文献[16]的基础上,改进了针对卷积神经网络的双流融合方法,总结了在深度卷积神经网络中的时间融合算法和空间融合算法,从而解决视频中动作识别的问题. Zhang X等[17]将特征融合思想引入深度学习模型中,提出了一种深度融合的学习架构,用于学习多媒体视频中高层语义特征.
以上介绍的特征融合算法的研究, 分析其本质可以分为的3类:第1类是基于贝叶斯决策理论的算法,它的基础是统计推断和估计理论,这类算法目的在于求解联合概率密度;第2类是基于稀疏表示理论的算法,这类算法通常与最优化理论相结合,将特征融合问题转化为优化问题,进而求解联合稀疏表示来达到融合目的;第3类是基于深度学习理论的算法,这种算法的主要思想是在深度卷积神经网络中加入特征融合过程,以改进网络模型.
3 特征融合算法在模式识别领域对特征融合方法的研究包括基于贝叶斯理论的特征融合、基于稀疏表示理论的特征融合算法等.近年来,随着深度学习理论的发展,基于深度学习理论的特征融合算法也逐渐成为研究热点.前两者是在提取样本多特征的基础上提出融合算法,重点在于对多特征进行综合处理得到融合特征;后者是将融合的思想引入深度学习理论中,在深度神经网络模型中加入融合过程,从而对网络模型进行优化.
3.1 基于贝叶斯理论的特征融合算法基于贝叶斯理论的特征融合算法是在分类器融合算法基础上发展起来的.贝叶斯决策理论是一种经典的模式识别方法.已知模型空间Ω包含C种模式类,记为Ω=(ω1,…,ωC),未知样本x由N维实数特征组成,记为x=[x1, x2, …, xN]N.根据最小错误率的贝叶斯决策理论,若将样本x分为第j类,则该类就是在已知样本x条件下后验概率最大的模式类,这个决策过程表示为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{x}} \to {\omega _j},}\\ {{\rm{if}}\;F\left( {{\omega _j}} \right) = \mathop {\max }\limits_{k = 1, \cdots ,C} P\left( {{\omega _k}\left| \mathit{\boldsymbol{x}} \right.} \right)} \end{array} $ | (1) |
其中:P(ωk|x)表示第k类的后验概率,k∈[1, C].
3.1.1 分类器融合的乘法规则与加法规则在式(1) 所示的决策过程中,如果将x看作分类器的输出结果,就可以得到基于贝叶斯理论的分类器融合算法.假设有M个分类器,对于给定模式类每个分类器的输出结果都通过不同度量向量进行表示,用xi表示第i个分类器输出结果的度量向量.这里为了区分,用Z表示一个未知样本,那么将样本Z进行分类的决策过程可以表示为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{Z}} \to {\omega _j},}\\ {{\rm{if}}\;F\left( {{\omega _j}} \right) = \mathop {\max }\limits_{k = 1, \cdots ,C} P\left( {{\omega _k}\left| {{\mathit{\boldsymbol{x}}_1}, \cdots ,{\mathit{\boldsymbol{x}}_M}} \right.} \right)} \end{array} $ | (2) |
其中:P(ωk|x1, …, xM)表示在已知M个分类器输出结果条件下第k类的后验概率,k∈[1, C].在此基础上,引入分类器独立性假设并结合式(3),就可以将联合类条件表示为各个分类器的类条件概率相乘的形式,得到分类器融合的乘法规则,用式(4) 表示,见文献[2].等式(3) 右侧分子中p(x1, …, xM|ωk)表示分类器的联合类条件概率.
| $ P\left( {{\omega _k}\left| {{\mathit{\boldsymbol{x}}_1}, \cdots ,{\mathit{\boldsymbol{x}}_M}} \right.} \right) = \frac{{P\left( {{\mathit{\boldsymbol{x}}_1}, \cdots ,{\mathit{\boldsymbol{x}}_M}\left| {{\omega _k}} \right.} \right)p\left( {{\omega _k}} \right)}}{{P\left( {{\mathit{\boldsymbol{x}}_1}, \cdots ,{\mathit{\boldsymbol{x}}_M}} \right)}} $ | (3) |
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{Z}} \to {\omega _j},}\\ {{\rm{if}}\;F\left( {{\omega _j}} \right) = \mathop {\max }\limits_{k = 1, \cdots ,C} {P^{ - \left( {M - 1} \right)}}\left( {{\omega _k}} \right)\prod\limits_{i = 1}^M {P\left( {{\omega _k}\left| {{\mathit{\boldsymbol{x}}_i}} \right.} \right)} } \end{array} $ | (4) |
其中P(ωk)表示第k类的先验概率.分类器独立性假设各个分类器的输出结果所服从的概率分布是相互独立的.为了解决第k类后验概率P(ωk|xi)为0时导致的分类错误问题,在乘法规则的基础上,再引入先验概率和后验概率近似相等假设,可以推导出分类器融合的加法规则,表示为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{Z}} \to {\omega _j},}\\ {{\rm{if}}\;F\left( {{\omega _j}} \right) = \mathop {\max }\limits_{k = 1} \left[ {\left( {1 - M} \right)P\left( {{\omega _k}} \right) + \prod\limits_{i = 1}^M {P\left( {{\omega _k}\left| {{\mathit{\boldsymbol{x}}_i}} \right.} \right)} } \right]} \end{array} $ | (5) |
其中:后验概率P(ωk|xi)采用相加的形式替代了式(4) 中相乘的形式,可以解决后验概率为0时的分类错误问题.先验概率和后验概率近似相等假设认为在各个分类器条件下的后验概率不会显著偏离该类的先验概率,表示为
| $ P\left( {{\omega _k}\left| {{\mathit{\boldsymbol{x}}_k}} \right.} \right) = P\left( {{\omega _k}} \right)\left( {1 + {\delta _{ki}}} \right) $ |
其中δki为一个极小值.
3.1.2 基于线性特征依赖模型的特征融合算法由于分类器独立性假设与先验概率和后验概率近似相等假设都有相应的成立条件,在各种应用情景中不一定完全成立,尤其是分类器独立性假设在许多分类问题中都难以成立.因此,Ma等[7]在此基础上进一步研究了线性依赖模型,并且针对特征级融合提出了线性特征依赖模型(LFDM, linear feature dependency modeling),实现了特征级融合.该模型通过增加线性依赖项αikP(ωk)δik来对分类器间的依赖关系进行建模, 其中αik表示第i个分类器的依赖权重,δik是一个极小值.式(4) 的后验概率可以表示为式(6) 的形式.
| $ \begin{array}{*{20}{c}} {P\left( {{\omega _k}\left| {{\mathit{\boldsymbol{x}}_1}, \cdots ,{\mathit{\boldsymbol{x}}_M}} \right.} \right) = \frac{{{p_0}}}{{P{{\left( {{\omega _k}} \right)}^{M - 1}}}}\prod\limits_{i = 1}^M {P\left( {{\omega _k}\left| {{\mathit{\boldsymbol{x}}_i}} \right.} \right)} + }\\ {\left. {\alpha _i^kP\left( {{\omega _k}} \right)\delta _i^k} \right),i \in \left[ {1,M} \right]} \end{array} $ | (6) |
| $ {P_0} = \frac{{\prod\limits_{i = 1}^M {p\left( {{x_i}} \right)} }}{{p\left( {{x_1}, \cdots ,{x_M}} \right)}} $ | (7) |
这里需要将xi, i∈[1, M]仍看作样本的Ni维特征向量,表示为xi=[xi1, xi2, …, xiNi]Ni.若进一步将xi向量的每个维度都看作一个分类器,则式(6) 的后验概率可以表示为
| $ \begin{array}{*{20}{c}} {P\left( {{\omega _k}\left| {{\mathit{\boldsymbol{x}}_1}, \cdots ,{\mathit{\boldsymbol{x}}_M}} \right.} \right) = }\\ {P\left( {{\omega _k}\left| {{x_{11}}, \cdots ,{x_{1{N_1}}}, \cdots ,{x_{M{N_1}}}, \cdots ,{x_{M{N_M}}}} \right.} \right)} \end{array} $ | (8) |
LFDM的推导过程如式(9) 所示.推导过程中,在第4步将
| $ \begin{array}{*{20}{c}} {P\left( {{\omega _k}\left| {{x_{11}}, \cdots ,{x_{1{N_1}}}, \cdots ,{x_{M{N_1}}}, \cdots ,{x_{M{N_M}}}} \right.} \right)}\\ {\frac{{{{p'}_0}}}{{p{{\left( {{\omega _k}} \right)}^{ - \left( {1 - \sum\limits_{i = 1}^M {{N_i}} } \right)}}}}\prod\limits_{i = 1}^M {\prod\limits_{n = 1}^{{N_i}} {\left( {P\left( {{\omega _k}\left| {{x_{in}}} \right.} \right) + } \right.} } }\\ {\left. {\alpha _{in}^kP\left( {{\omega _k}} \right)\delta _{in}^k} \right) = }\\ {\frac{{{{p'}_0}}}{{p{{\left( {{\omega _k}} \right)}^{ - \left( {1 - \sum\limits_{i = 1}^M {{N_i}} } \right)}}}}\prod\limits_{i = 1}^M {\prod\limits_{n = 1}^{{N_m}} {\left( {P\left( {{\omega _k}} \right)\left( {1 + \delta _{in}^k} \right) + } \right.} } }\\ {\left. {\alpha _{in}^kP\left( {{\omega _k}} \right)\delta _{in}^k} \right) = }\\ {{{P'}_0}P\left( {{\omega _k}} \right)\prod\limits_{i = 1}^M {\prod\limits_{n = 1}^{{N_i}} {\left( {1 + \delta _{in}^k + \alpha _{in}^k\delta _{in}^k} \right)\mathop = \limits^{1 + \alpha _{in}^k = \gamma _{in}^k} } } }\\ {{{P'}_0}P\left( {{\omega _k}} \right)\prod\limits_{i = 1}^M {\prod\limits_{n = 1}^{{N_i}} {\left( {1 + \gamma _{in}^k\delta _{in}^k} \right) = } } }\\ {{{P'}_0}P\left( {{\omega _k}} \right)\left( {1 + \gamma _{11}^k + \delta _{11}^k + \cdots + \gamma _{in}^k\delta _{in}^k + \cdots } \right) \approx }\\ {{{P'}_0}P\left( {{\omega _k}} \right)\left( {1 + \sum\limits_{i = 1}^M {\sum\limits_{n = 1}^{{N_i}} {\gamma _{in}^k\delta _{in}^k} } } \right) = }\\ {{{P'}_0}P\left( {{\omega _k}} \right)\left( {1 + \sum\limits_{i = 1}^M {\sum\limits_{n = 1}^{{N_i}} {\gamma _{in}^k\left( {\frac{{p\left( {{\omega _k}\left| {{x_{in}}} \right.} \right)}}{{p\left( {{\omega _k}} \right)}} - 1} \right)} } } \right) = }\\ {{{P'}_0}\left( {P\left( {{\omega _k}} \right) + \sum\limits_{i = 1}^M {\sum\limits_{n = 1}^{{N_i}} {\gamma _{in}^l\left( {p\left( {{\omega _k}\left| {{x_{in}}} \right.} \right) - p\left( {{\omega _k}} \right)} \right)} } } \right)} \end{array} $ | (9) |
| $ {{P'}_0} = \frac{{\prod\limits_{i = 1}^M {\prod\limits_{n = 1}^{{N_i}} {P\left( {{x_{in}}} \right)} } }}{{P\left( {{x_{11}}, \cdots ,{x_{1{N_1}}}, \cdots ,{x_{M{N_1}}}, \cdots ,{x_{M{N_M}}}} \right)}} $ | (10) |
LFDM不需要分类器独立性假设成立,因此在实际应用中适用范围更广,但是该模型仍然需要在先验概率和后验概率近似相等假设成立的条件下才能使用. LFDM不受特征维度的影响,相对于分类器级的融合算法,特征级融合算法能够直接利用样本的特征数据,对多种特征进行融合处理,可以解决分类问题中类内方差较小而类间方差较大的问题,从而提高模型的分类准确率.但是,该算法将特征量的每个维度都看作一个分类器,致使运算时间复杂度较高,有待改进.
3.2 基于稀疏表示理论的特征融合算法稀疏表示理论是信号处理领域的一种基础理论,它的基本思想是使用数据稀疏性这一先验知识,从一个超完备字典中找到尽可能少的原子对目标信号进行线性表示.稀疏表示问题可以表示为,对于向量b∈
| $ \begin{array}{*{20}{c}} {\min {{\left\| \mathit{\boldsymbol{x}} \right\|}_0}}\\ {{\rm{s}}{\rm{.t}}{\rm{.}}\;\mathit{\boldsymbol{Ax}} = \mathit{\boldsymbol{b}}} \end{array} $ | (11) |
基于稀疏表示理论的特征融合算法是对样本提取多特征后建立特征联合稀疏表示矩阵,这个稀疏表示矩阵就是多特征的融合结果.
3.2.1 基于联合稀疏表示的特征融合算法对于训练样本,已知有C种模式类和D种特征,用pj表示属于第j类的样本数量,那么样本总数为
| $ p = \sum\limits_{j = 1}^C {{p_j}} $ |
Xi表示对所有样本提取第i种特征后得到的特征向量矩阵,记为Xi=[X1i, X2i, …, Xci],i∈[1, D]称为一个字典;矩阵Xi中的第j个元素是属于第j类样本的特征向量矩阵,记为Xji=[Xj, 1i, Xj, 2i…, Xij, pj],j∈[1, C]称为子字典;矩阵Xji中的每一列是一个样本的特征向量,称为一个原子.因此,D种特征对应D个字典,第i种特征的维度记为ni,如图 2所示.

|
图 2 训练样本 |
用Y表示测试样本特征向量组成的集合,表示为Y={Y1, Y2, …, YD}.集合Y中第i个元素Yi是第i种特征的测试样本特征向量组成的矩阵,表示为Yi=[Y2i, Y2i, …, Yidi]∈
| $ d = \sum\limits_{i = 1}^D {{d_i}} $ |
矩阵中的每一列是一个测试样本,如图 3所示.
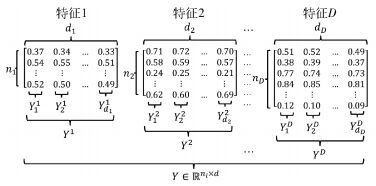
|
图 3 测试样本 |
根据稀疏表示理论,可以将测试样本矩阵Yi表示成字典Xi与稀疏矩阵Γi相乘的形式,记为
| $ {\mathit{\boldsymbol{Y}}^i} = {\mathit{\boldsymbol{X}}^i}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^i} + {\mathit{\boldsymbol{N}}^i},i = 1, \cdots ,D $ | (12) |
其中Ni是一个稀疏噪声矩阵.
因此,对于每种特征都有一个稀疏矩阵Γi与之对应,各个稀疏矩阵组合在一起可以得到联合稀疏表示矩阵Γ=[Γ1,Γ2, …, ΓD]∈
| $ \mathit{\boldsymbol{ \boldsymbol{\hat \varGamma} }} = \arg \mathop {\min }\limits_\mathit{\boldsymbol{ \boldsymbol{\varGamma} }} \frac{1}{2}\sum\limits_{i = 1}^D {\left\| {{\mathit{\boldsymbol{Y}}^i} - {\mathit{\boldsymbol{X}}^i}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^i}} \right\|_{\rm{F}}^2 + \lambda {{\left\| \mathit{\boldsymbol{ \boldsymbol{\varGamma} }} \right\|}_{1,q}}} $ | (13) |
| $ {\left\| \mathit{\boldsymbol{ \boldsymbol{\varGamma} }} \right\|_{1,q}} = \sum\limits_{k = 1}^p {{{\left\| {{\gamma ^k}} \right\|}_q}} $ | (14) |
得到矩阵Γ之后,通过式(15) 的分类判别函数可以对未知样本Y进行分类,输入D种特征,输出该样本的模式类标签.
| $ {\rm{identity}}\left( \mathit{\boldsymbol{Y}} \right) = \arg \mathop {\min }\limits_j \sum\limits_{i = 1}^D {\left\| {{\mathit{\boldsymbol{Y}}^i} - {\mathit{\boldsymbol{X}}^i}\delta _j^i\left( {{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^i}} \right)} \right\|_{\rm{F}}^2} $ | (15) |
其中δji是一个矩阵指示器函数,它对稀疏矩阵Γi中的值起到了选择的作用,即保持矩阵Γi与第j类相关行的值,而将其他行全部设置为0.
3.2.2 鲁棒的基于联合稀疏表示的特征融合算法对于图像中较严重的噪声,例如遮挡问题,可通过在式(12) 中增加噪声项来增强模型的鲁棒性,如式(16) 所示.在遮挡问题中,BiΛi是背景噪声项,Bi是基础遮挡样本,Λi是遮挡噪声稀疏矩阵.在得到Λi后,可以通过Yi-BiΛi来去除遮挡噪声.对于每种特征都有一个遮挡噪声稀疏矩阵与之对应,它们的联合稀疏表示矩阵记为Λ=[Λ1, Λ2, …, ΛD].
| $ {\mathit{\boldsymbol{Y}}^i} = {\mathit{\boldsymbol{X}}^i}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^i} + {\mathit{\boldsymbol{B}}^i}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^i} + {\mathit{\boldsymbol{N}}^i},i = 1,2, \cdots ,D $ | (16) |
增加了背景噪声项后,需要同时求解矩阵Γ和矩阵Λ,该问题可以表示为式(17),其中对施加l1范数的正则化,λ1和λ2是预设参数.在得到两个联合稀疏表示矩阵Γ和Λ后,通过式(18) 的分类判别函数可以对未知样本Y进行分类.
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{ \boldsymbol{\hat \varGamma} }},\mathit{\boldsymbol{ \boldsymbol{\hat \varLambda} }} = \arg \mathop {\min }\limits_{\mathit{\boldsymbol{ \boldsymbol{\varGamma} ,A}}} \frac{1}{2}\sum\limits_{i = 1}^D {\left\| {{\mathit{\boldsymbol{Y}}^i} - {\mathit{\boldsymbol{X}}^i}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^i} - } \right.} }\\ {\left. {{\mathit{\boldsymbol{B}}^i}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^i}} \right\|_{\rm{F}}^2 + {\lambda _1}{{\left\| \mathit{\boldsymbol{ \boldsymbol{\varGamma} }} \right\|}_{1,q}} + {\lambda _2}{{\left\| \mathit{\boldsymbol{ \boldsymbol{\varLambda} }} \right\|}_1}} \end{array} $ | (17) |
| $ {\rm{identity}}\left( \mathit{\boldsymbol{Y}} \right) = \arg \mathop {\min }\limits_j \sum\limits_{i = 1}^D {\left\| {{\mathit{\boldsymbol{Y}}^i} - {\mathit{\boldsymbol{X}}^i}\delta _j^i\left( \mathit{\boldsymbol{ \boldsymbol{\varGamma} }} \right) - {\mathit{\boldsymbol{B}}^i}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^i}} \right\|_{\rm{F}}^2} $ | (18) |
深度学习理论是在人工神经网络的基础上发展起来的机器学习理论,在多层神经网络中加入了更多隐层单元,得到了深度神经网络模型.其中深度卷积神经网络模型是该理论中的重要模型之一.使用该模型可以进行有监督地学习,将特征提取过程与分类器训练过程整合在一起,实现端到端的机器学习.基于深度学习理论的特征融合算法是将特征融合的思想引入深度神经网络模型,使用多特征输入到模型中进行训练,在模型中选择2个隐层进行特征融合.
Simonyan等[16]首先提出了一种使用双流架构的深度卷积神经网络模型,可解决视频中的动作识别问题.该模型分别建立一个空间流卷积神经网络和一个时间流卷积神经网络进行独立训练,在最终的Softmax分类输出层将这2个网络进行融合,属于分类器级的融合.而Feichtenhofer等[15]则在这个基础上改进了网络融合方法,提出了空间特征融合方法和时间特征融合算法,不仅可以在Softmax层进行融合,还可以在卷积层之后的ReLU层进行融合,实现特征级的融合.
3.3.1 空间特征融合算法空间特征融合算法可以对卷积层输出的2个特征图(feature map)进行融合,得到融合后的特征图,从而将2个深卷积神经网络模型连接在一起,这个连接点就是融合点.因此,引入特征融合方法之后,2个深卷积神经网络模型在融合点之前分别进行特征学习,并在融合点将独立学习的特征进行融合,最后开始共同学习.融合函数定义为
| $ f:\mathit{\boldsymbol{x}}_t^a + \mathit{\boldsymbol{x}}_t^b \to {\mathit{\boldsymbol{y}}_t} $ | (19) |
其中:xta和xtb表示t时刻的视频帧分别经过卷积运算得到的空间特征图,yt表示融合空间特征图,xa、xb、yt∈
加性融合函数ysum=fsum(xa, xb),是对2个特征图对应位置元素的值进行相加,如式(20) 所示,融合特征图的通道数不变,其中i∈[1, H],j∈[1, W],d∈[1, D].
| $ \mathit{\boldsymbol{y}}_{i,j,d}^{{\rm{sum}}} = \mathit{\boldsymbol{x}}_{i,j,d}^a + \mathit{\boldsymbol{x}}_{i,j,d}^b $ | (20) |
最大融合函数ymax=fmax(xa, xb)与加性融合函数相似,是将2个特征图对应的位置元素值较大的一个作为融合结果,即
| $ \mathit{\boldsymbol{y}}_{i,j,d}^{{\rm{max}}} = \max \left\{ {\mathit{\boldsymbol{x}}_{i,j,d}^a,\mathit{\boldsymbol{x}}_{i,j,d}^b} \right\} $ | (21) |
级联融合函数ycat=fcat(xa, xb)与前两者不同,它保留了2个特征图的结果,并将融合后特征图的通道数变为原始特征图的两倍,如
| $ \mathit{\boldsymbol{y}}_{i,j,2d}^{{\rm{cat}}} = \mathit{\boldsymbol{x}}_{i,j,d}^a,\mathit{\boldsymbol{y}}_{i,j,2d - 1}^{{\rm{cat}}} = \mathit{\boldsymbol{x}}_{i,j,d}^b $ | (22) |
其中y∈
卷积融合函数yconv=fconv(xa, xb),是将级联融合函数的融合结果与滤波器f进行卷积运算,并且引入偏差值b,从而实现融合特征图的降维处理.表示为
| $ {\mathit{\boldsymbol{y}}^{{\rm{conv}}}} = {\mathit{\boldsymbol{y}}^{{\rm{cat}}}}\mathit{\boldsymbol{f}} + \mathit{\boldsymbol{b}} $ | (23) |
其中f∈
双线性融合函数ybil=fbil(xa, xb),是对2个特征图对应的位置元素进行外积运算后求和,融合特征图的通道数是原始特征图通道数的平方,表示为
| $ {\mathit{\boldsymbol{y}}^{{\rm{bil}}}} = \sum\limits_{i = 1}^H {\sum\limits_{j = 1}^W {\mathit{\boldsymbol{x}}_{i,j}^{aT} \otimes \mathit{\boldsymbol{x}}_{i,j}^b} } $ | (24) |
其中ybil∈
时间特征融合算法主要作用在深度卷积神经网络的池化层.在进行池化处理之前,需要将空间特征图按照时序进行堆叠,使得输入池化层的特征图维度提高,表示为x1,…,T∈
3D池化方法是对深度卷积神经网络中通常使用的2D池化方法的直接扩展,使用HWT的3D池化立方代替原始池化层的计算方法,对输入的特征图x进行池化运算,从而将池化处理从空域扩展到时域. 3D池化立方可以使用最大池化方法,保留立方区域中的最大值作为池化结果.这种方法是对特征图的单通道进行处理,不进行跨通道的池化运算.
3D卷积+3D池化方法则是在3D池化方法基础上,再加入一个滤波器f∈
| $ {\mathit{\boldsymbol{y}}_{1, \cdots ,T}} = {\mathit{\boldsymbol{x}}_{1, \cdots ,T}} * f + \mathit{\boldsymbol{b}} $ | (25) |
计算得到的y1, …, T再进行3D池化处理.使用滤波器f可以在一个局部的时空邻域内对图像特征的组合,通过使用H′W′T′D的卷积核进行卷积运算,增加模型的连接权重数量.
在处理视频数据时,时间特征融合算法通常与空间特征融合算法同时使用,通过利用视频中的时序信息,提高基于视频的动作识别或者目标识别的准确率.
4 结束语随着人工智能研究的深入,特别是在解决图像识别问题中,特征融合方法受到广泛关注,无论是对特征融合方法本身的研究,还是结合特征融合方法改进现有方法,都成为目前研究的热点.笔者总结了近年来模式识别领域中特征融合方法的研究进展,基于信息融合理论介绍了特征融合方法的基本原理和发展现状,介绍和分析了基于叶贝斯理论的特征融合算法、基于稀疏表示理论的特征融合算法和基于深度学习理论的特征融合算法.
特征融合方法可以综合利用多种图像特征实现特征互补,在解决图像识别问题中,相对于单一特征而言,基于特征融合的图像识别方法具有更好的鲁棒性.笔者介绍的3种特征融合算法分别建立在不同的理论基础上,体现了特征融合思想的普适性.目前,对特征融合方法的研究主要集中在融合算法、融合模型等方面,在融合特征选择、基础理论等方面也会有进一步的研究.
| [1] | Sanderson C, Paliwal K K. Identity verification using speech and face information[J]. Digital Signal Processing, 2004, 14(5): 449–480. doi: 10.1016/j.dsp.2004.05.001 |
| [2] | Kittler J, Hatef M, Duin R P W, et al. On combining classifiers[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1998, 20(3): 226–239. doi: 10.1109/34.667881 |
| [3] | 韩崇昭, 朱洪艳, 段战胜, 等. 多源信息融合[M]. 北京: 清华大学出版社, 2010. |
| [4] | Kuncheva L I. A theoretical study on six classifier fusion strategies[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(2): 281–286. doi: 10.1109/34.982906 |
| [5] | Jain A, Nandakumar K, Ross A. Score normalization in multimodal biometric systems[J]. Pattern Recognition, 2005, 38(12): 2270–2285. doi: 10.1016/j.patcog.2005.01.012 |
| [6] | Nandakumar K, Chen Y, Dass S C, et al. Likelihood ratio-based biometric score fusion[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 30(2): 342. |
| [7] | Ma A J, Yuen P C, Lai J H. Linear dependency modeling for classifier fusion and feature combination[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(5): 1135–1148. doi: 10.1109/TPAMI.2012.198 |
| [8] | Shekhar S, Patel V M, Nasrabadi N M, et al. Joint sparse representation for robust multimodal biometrics recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36(1): 113–126. doi: 10.1109/TPAMI.2013.109 |
| [9] | Yan J, Zheng W, Xu Q, et al. Sparse kernel reduced-rank regression for bimodal emotion recognition from facial expression and speech[J]. IEEE Transactions on Multimedia, 2016, 18(7): 1319–1329. doi: 10.1109/TMM.2016.2557721 |
| [10] | Bai S, Bai X. Sparse contextual activation for efficient visual re-ranking[J]. IEEE Transactions on Image Processing, 2016, 25(3): 1056–1069. doi: 10.1109/TIP.2016.2514498 |
| [11] | Zhang L, Zhang D. Visual understanding via multi-feature shared learning with global consistency[J]. IEEE Transactions on Multimedia, 2016, 18(2): 247–259. doi: 10.1109/TMM.2015.2510509 |
| [12] | Yu M, Liu L, Shao L. Structure-preserving binary representations for RGB-D action recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(8): 1651–1664. doi: 10.1109/TPAMI.2015.2491925 |
| [13] | Demirkus M, Precup D, Clark J, et al. Hierarchical spatio-temporal probabilistic graphical model with multiple feature fusion for binary facial attribute classification in real-world face videos[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(6): 1185–1203. doi: 10.1109/TPAMI.2015.2481396 |
| [14] | Hu J F, Zheng W S, Lai J, et al. Jointly learning heterogeneous features for RGB-D activity recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016(99): 1–1. |
| [15] | Feichtenhofer C, Pinz A, Zisserman A. Convolutional two-stream network fusion for video action recognition[C]//CVPR 2016. Las Vegas:IEEE Computer Society, 2016:1933-1941. |
| [16] | Simonyan K, Zisserman A. Two-stream convolutional networks for action recognition in videos[J]. Advances in Neural Information Processing Systems, 2014, 1(4): 568–576. |
| [17] | Zhang X, Zhang H, Zhang Y, et al. Deep fusion of multiple semantic cues for complex event recognition[J]. IEEE Transactions on Image Processing, 2016, 25(3): 1033–1046. doi: 10.1109/TIP.2015.2511585 |


