2. 哈尔滨工业大学机器人技术与系统国家重点实验室, 哈尔滨 150001
根据仿人机器人协作运动的控制特点,构建2个仿人机器人进行球体搬运协作运动模型,并提出了一种基于二阶锥控制原理的多仿人机器人运动稳定性的控制方法.通过对协作运动过程中各种稳定性进行联合约束,构建二阶锥规划方程,将运动稳定性最优控制问题转换成二阶锥规划方程的优化问题.仿真与实验结果表明,该控制方法可以有效控制仿人机器人的协作运动并确保其稳定性.
2. State Key Laboratory of Robotics and System, Harbin Institute of Technology, Harbin 150001, China
According to the characteristics of cooperative motion control of humanoid robot, a cooperative motion model of two humanoid robot in ball handling was deduced and a control method based on second order cone principle was introduced to maintain the stability in movement for multi-robot.By deducing constraints of stability in cooperative movement, an equation of second-order cone programming was constructed, and the stability control problem was converted for solving equations of second order cone.Finally, the effectiveness of the proposed method is verified by simulation and experiment.
随着工业和服务业领域机器人的广泛应用,多机器人协作可以提高机器人系统的灵活性和有效性,同时为人机共融系统的研究提供有益帮助.
目前国内外对移动机器人的协作任务研究较多[1-3],在仿人机器人协作任务方面,机器人足球运动是比较典型的研究内容[4-5],Donner等[6]研究了人与仿人机器人协作完成一项任务的控制方式.然而,这些研究都建立在协作策略的层面[7],针对仿人机器人协作完成任务的运动规划层面展开的研究尚不多见. Choi等[8]认为机器人的零力矩点(ZMP,zero moment point)和重心的雅各比矩阵是平衡所需的基本因素,在机器人的运动过程中,可以通过嵌入重心矩阵的方式来控制其运动.由于多仿人机器人是一个多自由度的复杂联合控制系统,在运动控制中,单独的ZMP不能有效地对机器人的稳定性能进行优化,需要考虑重心和力矩等因素,引入其他稳定性判断准则,结合不同环境下的摩擦力等约束,共同达到有效控制机器人稳定的目的[9].
对2个仿人机器人的球体搬运协作任务进行运动学建模,采用二阶锥控制方法,对协作系统的稳定性进行联合约束,有效地控制了机器人的协作运动.
1 模型构建以2个仿人机器人共同协作搬运一个空心管子为任务,为了验证协作的有效性,在管子内部放置一个圆球,当管子两端高度不同时,该球会因为重力缘故做相应的滚动.为了使管内的球在B1和B2区间内滚动,确保能够顺利搬运管子,需要对2个仿人机器人的手臂运动进行协同控制.仿人机器人协作搬运管子的示意图如图 1所示.它以可任意移动的球体为模型,对仿人机器人的手臂可以实时进行运动控制,体现仿人特性,同时也具有搬运协作任务的普遍特性.

|
图 1 仿人机器人协作搬运管子示意图 |
假设仿人机器人R1在抬球运动过程中,2个仿人机器人的手部都处于同一水平线上,其中一个仿人机器人的手部距离地面的垂直高度为h,左右高度差为d,则另外一个仿人机器人R2的手部距离地面的垂直高度为h-d.设球为质点,其滚动速度为v0.其中,d、v0均可正可负,也可为零.机器人反应时间为t0,手部最低距离地面的垂直高度为h1,最高距离地面的垂直高度为h2,O为坐标系原点,管内球体活动的区间两端B1、B2分别对应于坐标系中的x1和x2.设坐标系向右方向为正,即x1 <0< x2.球所在位置为x,管子长度为L,球受到的摩擦力为f. R1、R2的手部沿竖直方向的速度分别为v1、v2.设v1、v2均以向上方向为正方向.
由于仿人机器人的手部高度受上下摆动的限制,任何时刻均需满足
| $ {h_1} - h \le \int_0^t {{v_1}} {\rm{d}}\mathit{t} \le {h_2} - h $ | (1) |
| $ {h_1} - \left( {h - d} \right) \le \int_{^{{t_0}}}^t {{v_2}} {\rm{d}}\mathit{t} \le {h_2} - \left( {h - d} \right) $ | (2) |
当t < t0时,R1、R2手部的高度差为
| $ \frac{{\int_0^t {{v_1}} {\rm{d}}\mathit{t} + d}}{{\sqrt {{L^2} + {{\left( {\int_0^t {{v_1}} {\rm{d}}\mathit{t} + d} \right)}^2}} }}mg $ |
其中:m为球的质量,g为重力加速度.
球体距离开始位置x的位移为
| $ \int_0^t {\left[ {{v_0} + \int_0^t {\left( {\frac{{\frac{{\int_0^t {{v_1}} {\rm{d}}\mathit{t} + d}}{{\sqrt {{L^2} + {{\left( {\int_0^t {{v_1}} {\rm{d}}\mathit{t} + d} \right)}^2}} }}mg - f}}{m}} \right)} {\rm{d}}\mathit{t}} \right]} {\rm{d}}\mathit{t} $ |
上述位移应满足以下约束条件
| $ \begin{array}{*{20}{c}} {{\mathit{x}_1} - x \le }\\ {\int_0^t {\left[ {{v_0} + \int_0^t {\left( {\frac{{\frac{{\int_0^t {{v_1}} {\rm{d}}\mathit{t} + d}}{{\sqrt {{L^2} + {{\left( {\int_0^t {{v_1}} {\rm{d}}\mathit{t} + d} \right)}^2}} }}mg - f}}{m}} \right)} {\rm{d}}\mathit{t}} \right]} {\rm{d}}\mathit{t} \le }\\ {{x_2} - x} \end{array} $ | (3) |
当t=t0时,R1、R2手部的高度差为
| $ {{d_{{t_0}}} = d + \int_0^{{t_0}} {{v_1}} {\rm{d}}\mathit{t}} $ | (4) |
| $ \begin{array}{*{20}{c}} {{x_{{t_0}}} = x + }\\ {\int_0^{{t_0}} {\left[ {{v_0} + \int_0^{{t_0}} {\left( {\frac{{\frac{{\int_0^{{t_0}} {{v_1}} {\rm{d}}\mathit{t} + d}}{{\sqrt {{L^2} + {{\left( {\int_0^{{t_0}} {{v_1}} {\rm{d}}\mathit{t} + d} \right)}^2}} }}mg - f}}{m}} \right)} {\rm{d}}\mathit{t}} \right]} {\rm{d}}\mathit{t}} \end{array} $ | (5) |
| $ {v_{{t_0}}} = {v_0} + \int_0^{{t_0}} {\left( {\frac{{\frac{{\int_0^{{t_0}} {{v_1}} {\rm{d}}\mathit{t} + d}}{{\sqrt {{L^2} + {{\left( {\int_0^{{t_0}} {{v_1}} {\rm{d}}\mathit{t} + d} \right)}^2}} }}mg - f}}{m}} \right)} {\rm{d}}\mathit{t} $ | (6) |
当t>t0时,R1、R2手部的高度差为
| $ \frac{{\int_{{t_0}}^t {\left( {{\mathit{v}_1} - {\mathit{v}_2}} \right)} {\rm{d}}\mathit{t} + {d_{{t_0}}}}}{{\sqrt {{L^2} + {{\left( {\int_{{t_0}}^t {\left( {{\mathit{v}_1} - {\mathit{v}_2}} \right)} {\rm{d}}\mathit{t} + {d_{{t_0}}}} \right)}^2}} }}mg $ |
球体距离开始位置x的位移为
| $ \int_{{t_0}}^t {\left[ {{v_{{t_0}}} + \int_{{t_0}}^t {\left( {\frac{{\frac{{\int_{{t_0}}^t {\left( {{\mathit{v}_1} - {\mathit{v}_2}} \right)} {\rm{d}}\mathit{t} + {d_{{t_0}}}}}{{\sqrt {{L^2} + {{\left( {\int_{{t_0}}^t {\left( {{\mathit{v}_1} - {\mathit{v}_2}} \right)} {\rm{d}}\mathit{t} + {d_{{t_0}}}} \right)}^2}} }}mg - f}}{m}} \right)} {\rm{d}}\mathit{t}} \right]} {\rm{d}}\mathit{t} $ |
上述位移应满足以下约束条件
| $ {\mathit{x}_1} - {x_{{t_0}}} \le \int_{{t_0}}^t {\left[ {{v_{{t_0}}} + \int_{{t_0}}^t {\left( {\frac{{\frac{{\int_{{t_0}}^t {\left( {{\mathit{v}_1} - {\mathit{v}_2}} \right)} {\rm{d}}\mathit{t} + {d_{{t_0}}}}}{{\sqrt {{L^2} + {{\left( {\int_{{t_0}}^t {\left( {{\mathit{v}_1} - {\mathit{v}_2}} \right)} {\rm{d}}\mathit{t} + {d_{{t_0}}}} \right)}^2}} }}mg - f}}{m}} \right)} {\rm{d}}\mathit{t}} \right]} {\rm{d}}\mathit{t} \le {\mathit{x}_2} - {x_{{t_0}}} $ | (7) |
在式(7) 中,代入已知的
| $ \begin{array}{*{20}{c}} {{x_1} - \left( {x + \int_0^{_{{t_0}}} {\left( {{v_0} + \int_0^{{t_0}} {\left( {\frac{{\frac{{\int_0^{{t_0}} {{v_1}} {\rm{d}}\mathit{t} + d}}{{\sqrt {{L^2} + {{\left( {\int_0^{{t_0}} {{v_1}} {\rm{d}}\mathit{t} + d} \right)}^2}} }}mg - f}}{m}} \right){\rm{d}}\mathit{t}} } \right)} {\rm{d}}\mathit{t}} \right) \\\le \int_{{t_0}}^t {\left[ {{v_0} + \int_0^{{t_0}} {\left( {\frac{{\frac{{\int_0^{{t_0}} {{v_1}} {\rm{d}}\mathit{t} + d}}{{\sqrt {{L^2} + {{\left( {\int_0^{{t_0}} {{v_1}} {\rm{d}}\mathit{t} + d} \right)}^2}} }}mg - f}}{m}} \right)} } \right.} {\rm{d}}\mathit{t} + }\\ {\int_{{t_0}}^t {\left[ {{v_{{t_0}}} + \int_{{t_0}}^t {\left( {\frac{{\frac{{\int_{{t_0}}^t {\left( {{v_1} - {v_2}} \right){\rm{d}}\mathit{t} + {\mathit{d}_{{\mathit{t}_0}}}} }}{{\sqrt {{L^2} + {{\left( {\int_{{t_0}}^t {\left( {{v_1} - {v_2}} \right){\rm{d}}\mathit{t} + {\mathit{d}_{{\mathit{t}_0}}}} } \right)}^2}} }}mg - f}}{m}} \right){\rm{d}}\mathit{t}} } \right]} {\rm{d}}\mathit{t} \le }\\ {{x_2} - \left( {x + \int_{00}^t {\left[ {{v_0} + \int_0^{{t_0}} {\left( {\frac{{\frac{{\int_0^{{t_0}} {{v_1}{\rm{d}}\mathit{t} + \mathit{d}} }}{{\sqrt {{L^2} + {{\left( {\int_0^{{t_0}} {{v_1}{\rm{d}}\mathit{t} + \mathit{d}} } \right)}^2}} }}mg - f}}{m}} \right){\rm{d}}\mathit{t}} } \right]} {\rm{d}}\mathit{t}} \right)} \end{array} $ | (8) |
可见,根据仿人机器人的手臂运动来控制球体的移动位置,可以确保2个仿人机器人的协作任务顺利完成.
2 构造仿人机器人协作运动的平衡约束与其他类型机器人相比较,仿人机器人具有重心高、足部支撑面小等特点.因此,在仿人机器人运动过程中,稳定性成为首要考虑的因素,尤其是2个机器人进行协作任务时,更需要对机器人之间的稳定性进行控制,才能确保任务顺利进行.目前,ZMP是仿人机器人运动中稳定性判断的最好依据之一[8],世界上大多数双足步行机器人系统都采用ZMP作为稳定行走的判据.综合ZMP、机器人运动时所受摩擦力以及机器人的手臂动能这3项因素,对仿人机器人施行运动约束,可有效提高仿人机器人运动中稳定性.
2.1 ZMP约束当仿人机器人的ZMP处于多边形A内部时,其足部的ZMP范围可以表示为[9]
| $ {p_{{\rm{zmp}}}} \in \left\{ {\sum\limits_{i = 1}^N {{\alpha _i}{p_i}\left| {{p_i} \in A\left( {i = 1,2, \cdots ,N} \right)} \right.} } \right\} $ | (9) |
其中:pi为机器人足部支持域内的点,pi∈A(i=1, 2, …N);αi为所在地面作用力的分量比,
设As为系数矩阵,bs为范围矢量,可得与式(9) 具有相同含义的式(10)
| $ {\mathit{\boldsymbol{A}}_s}{p_{{\rm{zmp}}}} + {\mathit{\boldsymbol{b}}_s} \le 0 $ | (10) |
一般情况下,在满足式(9) 的前提下,把理想ZMP轨迹
| $ \left\| {{p_{{\rm{zmp}}}} - p_{{\rm{zmp}}}^d} \right\| \le {\mathit{\varepsilon }_{{\rm{zmp}}}} $ | (11) |
仿人机器人足部与地面之间的摩擦力满足以下约束方程
| $ \left\| {{\mathit{\boldsymbol{P}}_{xy}}{F_0}} \right\| \le \mathit{\mu }{F_1} $ | (12) |
| $ \left\| {{\mathit{\boldsymbol{P}}_{mz}}{F_0} - {p_{{\rm{zmp}}}}{\mathit{\boldsymbol{P}}_{xy}}{F_0}} \right\| \le {\mathit{\mu }_r}{F_2} $ | (13) |
| $ {F_1} + {F_2} \le {\mathit{\boldsymbol{P}}_z}{F_0} $ | (14) |
其中:Pxy、Pmz和Pz是投影矩阵,分别表示x-y平面内的力向量、z坐标相切力和z坐标上的力向量;μ表示摩擦系数;μr表示机器人扭动摩擦系数;F0、F1和F2分别表示机器人在前向运动、切向运动和正常运动时受到的摩擦阻力.式(14) 表示机器人在行走过程中受力的约束情况.
2.3 手臂动能约束仿人机器人在手臂摆动转关节角度的时候,设角度向量q=
| $ T\left( t \right) = \sum\limits_{\iota = 1}^L {q\left( \iota \right)} p\left( \iota \right) = {\mathit{\boldsymbol{p}}^T}\left( \iota \right)\mathit{\boldsymbol{q}} $ | (15) |
其中:
在连续时间上分别进行采样,采样点为k=1,2,…,K,则求解仿人机器人动态平衡问题可以转化为求解式(16) 的误差加权范数最小问题.
| $ {\left\{ {\sum\limits_{k = 1}^K {{\lambda _k}{{\left| {{T_d}\left( {{t_k}} \right) - T\left( {{t_k}} \right)} \right|}^p}} } \right\}^{\frac{1}{p}}} $ | (16) |
其中Td(tk)为非负的加权系数,表示tk时刻的期望响应,其作用是协调不同参数之间拟合紧密程度.通常,求解该问题的误差范数时,取p=1,2或∞,则对应的动能控制问题可分别由以下范数准则表示
| $ \mathop {\min }\limits_q \sum\limits_{k = 1}^K {\left( {{\lambda _k}\left| {{T_d}\left( {{t_k}} \right) - {\mathit{\boldsymbol{p}}^T}\left( {{t_k}} \right)\mathit{\boldsymbol{q}}} \right|} \right)} $ | (17) |
| $ \mathop {\min }\limits_q {\sum\limits_{k = 1}^K {{\lambda _k}\left| {{T_d}\left( {{t_k}} \right) - {\mathit{\boldsymbol{p}}^T}\left( {{t_k}} \right)\mathit{\boldsymbol{q}}} \right|} ^2} $ | (18) |
| $ \mathop {\min }\limits_q \mathop {\max }\limits_k \left( {{\lambda _k}\left| {{T_d}\left( {{t_k}} \right) - {\mathit{\boldsymbol{p}}^T}\left( {{t_k}} \right)\mathit{\boldsymbol{q}}} \right|} \right) $ | (19) |
其中λk表示范数系数.
3 SOCP的构造与解法二阶锥规划(SOCP,second-order cone programming)理论是在20世纪70年代提出的,被证实为一种兼顾多个指标的优化设计方法[8-9].该方法已经在滤波器和波束形成器设计的优化方面得到了广泛的应用[10].基于该控制方法的优点,引入该方法用于对多仿人机器人协作运动控制和稳定性设计进行优化控制.
以式(18) 表示的范数准则为例[11].
对于一组非负的向量εk(k=1, 2, …, K),式(15) 改写为
| $ \begin{array}{*{20}{c}} {\mathop {\min }\limits_q \sum\limits_{k = 1}^K {\left( {{\lambda _k}{\mathit{\boldsymbol{\varepsilon }}_k}} \right)满足于} }\\ {{{\left| {{T_d}\left( {{t_k}} \right) - {\mathit{\boldsymbol{p}}^T}\left( {{t_k}} \right)\mathit{\boldsymbol{q}}} \right|}^2} \le {\mathit{\boldsymbol{\varepsilon }}_k},k = 1,2, \cdots ,K} \end{array} $ | (20) |
约束公式为式(8) 与式(21)~(25)
| $ {\mathit{\boldsymbol{A}}_s}{p_{{\rm{zmp}}}} + {\mathit{\boldsymbol{b}}_s} \le 0 $ | (21) |
| $ \left\| {{p_{{\rm{zmp}}}} - p_{{\rm{zmp}}}^d} \right\| \le {\mathit{\varepsilon }_{{\rm{zmp}}}} $ | (22) |
| $ \left\| {{\mathit{\boldsymbol{P}}_{xy}}{F_0}} \right\| \le \mathit{\mu }{F_1} $ | (23) |
| $ \left\| {{\mathit{\boldsymbol{P}}_{mz}}{F_0} - {p_{{\rm{zmp}}}}{\mathit{\boldsymbol{P}}_{xy}}{F_0}} \right\| \le {\mathit{\mu }_r}{F_2} $ | (24) |
| $ {F_1} + {F_2} \le {\mathit{\boldsymbol{P}}_z}{F_0} $ | (25) |
由式(20) 中的二次不等式约束|Td(tk)-pT(tk)q|2≤εk,可以得到
| $ \begin{array}{l} {\left\| {\begin{array}{*{20}{c}} {2{T_d}\left( {{t_k}} \right) - 2{\mathit{\boldsymbol{p}}^T}\left( {{t_k}} \right)\mathit{\boldsymbol{q}}}\\ {{\mathit{\boldsymbol{\varepsilon }}_k} - 1} \end{array}} \right\|^2} \le {\left( {{\mathit{\boldsymbol{\varepsilon }}_k} + 1} \right)^2}\\ \;\;\left\| {\begin{array}{*{20}{c}} {2{T_d}\left( {{t_k}} \right) - 2{\mathit{\boldsymbol{p}}^T}\left( {{t_k}} \right)\mathit{\boldsymbol{q}}}\\ {{\mathit{\boldsymbol{\varepsilon }}_k} - 1} \end{array}} \right\| \le {\mathit{\boldsymbol{\varepsilon }}_k} + 1 \end{array} $ | (26) |
给定y=[ε1, ε2, …, εK, qT]T,b=[λ1, λ2, …, λK, 01×L]T,使bTy=
| $ \begin{array}{*{20}{c}} {\mathop {\min }\limits_y {\mathit{\boldsymbol{b}}^\mathit{T}}满足于}\\ {\left\| {\left[ {\begin{array}{*{20}{c}} {2{T_d}\left( {{t_k}} \right)}\\ { - 1} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {{0_{1 \times K}}}&{2{\mathit{\boldsymbol{p}}^T}\left( {{t_k}} \right)}\\ { - {\mathit{\boldsymbol{m}}^\mathit{T}}\left( k \right)}&{{0_{1 \times L}}} \end{array}} \right]\mathit{\boldsymbol{y}}} \right\| \le 1 + }\\ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{m}}^\mathit{T}}\left( k \right)}&{{0_{1 \times L}}} \end{array}} \right]\mathit{\boldsymbol{y}}}\\ {k = 1,2, \cdots ,K} \end{array} $ | (27) |
其中m(k)=[m1, m2, …, mn, …, mK]T,
| ${m_i} = \left\{ {\begin{array}{*{20}{c}} {0,\quad n \ne k,}\\ {1,\quad n \ne k.} \end{array}} \right.$ |
对于式(27),可采用罚函数中的内点法[12]求解,在此不再赘述.
4 仿真与实验使用Matlab内嵌的SOCP工具包对稳定性控制问题的最优化进行仿真,并采用控制领域常用的最小均方(LMS,least mean square)自适应方法和SOCP方法进行比较.在优化效果方面,因粒子群算法(PSO,particle swarm optimization)在智能优化效果方面成绩突出,仿真中也将SOCP算法和PSO算法做了比较.
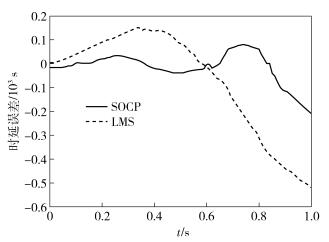
设每个仿人机器人运动时与地面之间的摩擦系数为μ=0.4,关节扭动摩擦系数μr=0.45.实验测试时间设定为1 s,对机器人的协作运动研究而言,这个时间已足够满足其瞬时运动的稳定性要求,时间片节点设置为0.1 s,仿人机器人运动速度设置为v=0.3 m/s,仿人机器人质量m=1 kg.经计算,该机器人的动能期望值为0.045 J,SOCP和LMS 2种方法在动能和时延误差方面的仿真对比结果如图 2和图 3所示.

|
图 2 动能比较 |
|
图 3 时延误差比较 |
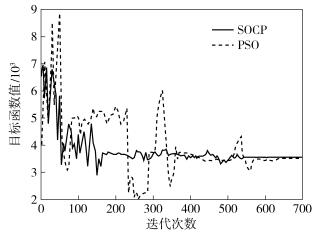
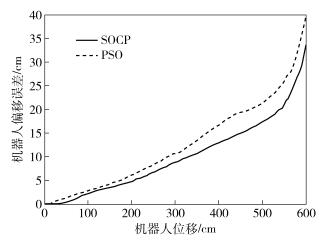
图 4和图 5分别为SOCP算法与PSO算法在迭代误差效果方面和位移误差效果方面的比较图.其中,粒子群的维数设为28,个数设为30,学习因子c1、c2取2,惯性权重w取0.7,迭代步数取700.设定2个仿人机器人在协作运动中都是沿直线运动,其距离设定为6 m.
|
图 4 迭代误差效果比较 |
|
图 5 位移误差效果比较 |
从图 4可以看到,PSO方法的震荡始终比较强烈,以至于在接近迭代580步的时候才趋于平稳,而SOCP的迭代最初收敛速度要比PSO快,并且在迭代步数到280左右的时候开始往最优值靠近.在2个机器人协作运动行走6 m的过程中,因缺乏必要的导航,使其偏离了一定的预期轨道,从图 5可以看到,针对式(27) 求解,SOCP控制方法要优于PSO方法.
实物实验时,采用2台NAO型仿人机器人进行协作运动实验. NAO的版本为V5.协作运动截图如图 6所示.

|
图 6 NAO机器人协作运动实物截图 |
打开NAO机器人的足部受力监控窗口,截取运动过程中的部分受力实时反馈曲线图,2台机器人脚部的实时受力情况如图 7和图 8所示,其中图 7为运动之前NAO机器人受力实时反馈曲线截图,图 8为运动时NAO机器人受力实时反馈曲线截图,虚线和实线分别表示不同的机器人足部受力情况.从图 7和图 8中可以看到,2台机器人足部的受力区别相差不是很多,在协作运动过程中波动也不是很大,说明机器人能较好完成协作运动.

|
图 7 运动前机器人受力实时反馈曲线截图 |

|
图 8 运动时机器人受力实时反馈曲线截图 |
仿人机器人协作运动控制系统是一个多自由度的非线性最优控制系统,针对其稳定控制的复杂性,用SOCP控制方法将运动稳定性最优化控制问题转换成SOCP的优化问题,并使用Matlab仿真软件内嵌SOCP工具包对机器人运动控制问题进行仿真测试,同时与各种常用方法进行了比较分析.仿真结果表明,该方法对于复杂的含约束的仿人机器人稳定性控制优化问题十分有效,特别是当优化参数减少时,该方法可以实现在线优化.实物实验结果也表明,该控制方法可以有效地控制仿人机器人的协作运动,并确保其运动的稳定性.
| [1] |
孟石, 戴先中, 甘亚辉. 多机器人协作系统轨迹约束关系分析及示教方法[J]. 机器人, 2012, 34(5): 546–552.
Meng Shi, Dai Xianzhong, Gan Yahui. Path constraint relation and trajectory teaching method for multi-robot cooperation system[J]. Robot, 2012, 34(5): 546–552. |
| [2] | Li Shuai, Guo Yi, Bingham B. Multi-robot cooperative control for monitoring and tracking dynamic plumes[C]//2014 IEEE International Conference on Robotics and Automation (ICRA). Hong Kong:IEEE, 2014:980-986. |
| [3] | Pippin C, Christensen H. Trust modeling in multi-robot patrolling[C]//2014 IEEE International Conference on Robotics and Automation (ICRA). Hong Kong:IEEE, 2014:1120-1126. |
| [4] | 郗俊杰. 多智能双足机器人的动作控制及协作研究[D]. 西安: 西安电子科技大学, 2012. |
| [5] |
蓝冬英, 丛杨, 程立英, 等. 基于仿人足球机器人协作定位技术研究[J]. 机器人技术与应用, 2012(6): 42–44.
Lan Dongying, Cong Yang, Cheng Liying, et al. Research on cooperation location based on humanoid soccer robot[J]. Robot Technology and Application, 2012(6): 42–44. |
| [6] | Donner P, Christange F, Martin Buss. Human-robot cooperative swinging of complex pendulum-like objects[C]//2013 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Tokyo:IEEE, 2013:467-472. |
| [7] | Ahmad A, Nascimento T, Conceição A G S, et al. Perception-driven multi-robot formation control[C]//2013 IEEE International Conference on Robotics and Automation (ICRA). Karlsruhe:IEEE, 2013:1122-1128. |
| [8] | Choi Y, Kim D, O h, Y. You B J. Walking control of humanoid robot based on the kinematic resolution of CoM Jacobian with embedded motion[J]. IEEE Transaction on Robotics, 2012, 23(6): 1285–1293. |
| [9] | Yan Shefeng, Ma Yuanliang. A unified framework for designing FIR filters with arbitrary magnitude and phase reponse[J]. Digital Signal Processing, 2004, 14(6): 510–522. doi: 10.1016/j.dsp.2004.08.003 |
| [10] | Bai Y Q. Ghami M EI, Roos C. A comparative study of kernel functions for primal-dual interior-point algorithms in linear optimization[J]. SIAM Journal on Optimization, 2005, 15(1): 101–128. |
| [11] | Vukobratovic M, Stepanenko J. On the stability of anthropomorphic systems[J]. Mathematical Biosciences, 1972, 15: 1–37. doi: 10.1016/0025-5564(72)90061-2 |
| [12] | Lobo M S, Vandenberghe L, Boyd S, et al. Applications of second-order cone programming[J]. Linear Algebra and its Application, 1998, 204(1-3): 193–22. |


