2. 西安交通大学 电子信息工程学院, 西安 710049
基于自适应滤波的传统稀疏信道估计方法大多基于高斯噪声模型的假设,当环境噪声包含冲击噪声时,信道估计性能将严重恶化.为了解决冲击噪声环境下的稀疏信道估计问题,提出了一种基于梯度向量混合范数的稳健变步长符号算法.仿真结果表明,提出的算法在高斯噪声和冲击噪声环境下达到了预期的效果.
2. School of Electronic and Information Engineering, Xi'an Jiaotong University, Xi'an 710049, China
In the broadband wireless communication system, the methods of adaptive sparse channel estimation can improve the accuracy of the channel estimation since it can make full use of the inherent sparseness of the channel. However, most of traditional sparse channel estimation methods are based on the hypothesis of Gaussian noise models, the channel estimation performance will be severely deteriorated when environmental noise contains impulsive noise. To deal with this problem, a robust variable step-size sign algorithm based on mixed norm of gradient vector was proposed. Simulations demonstrate that the proposed algorithm achieves the expected performance in Gaussian noise and impulsive noise environment.
随着近年来移动通信标准逐步向第五代通信系统演进,宽带通信技术,如超宽带技术等扮演着越来越重要的作用.由于无线通信系统受到多径传播以及环境噪声等影响,如何获得准确的信道状态信息成为了实现相干解调、信号检测等环节的关键[1-2].传统的线性信道估计方法,如最小二乘法等,是基于密集信道脉冲响应的前提下实现的.然而,相关研究[3]表明,宽带无线通信系统的多径信道往往具有显著的稀疏性,因此,稀疏信道估计方法成为近年来的研究热点.为了充分利用信道的稀疏性,相关研究提出了一些带有损耗函数的自适应信道估计方法,如在归一化最小均方(NLMS, normalized least mean square)算法的基础上提出的Lp范数及L0范数NLMS算法[4]、趋零NLMS(ZA-NLMS, zero-attracting NLMS)算法[5]以及加权ZA-NLMS(RZA-NLMS, re-weighted ZA-NLMS)算法[6]等.近年来又有一系列关于变步长算法的研究,如趋零变步长NLMS(ZA-VSS-NLMS, zero-attracting variable step-size NLMS)算法以及加权ZA-VSS-NLMS(RZA-VSS-NLMS, re-weighted ZA-VSS-NLMS)算法[7]等.这些方法具有更准确的收敛精度,但往往仅适用于高斯噪声环境,而忽视了环境中潜在的冲击噪声.这种冲击噪声通常由自然或人为产生的电磁波构成,具有长尾分布等特点[1-2],因而不满足高斯噪声的假设.因此,需要研究稳健的信道估计方法来克服冲击噪声的影响.
为了提高稀疏信道估计的精度并克服冲击噪声对信道估计的干扰,笔者将符号算法与损耗函数相结合,并通过使用一种基于混合范数的变步长方法进一步提高算法的估计精度及收敛速度.仿真结果表明,所提出的算法相较于传统算法具有更快的收敛速度,对冲击噪声具有较强的稳健性,并且当信道状态信息发生改变时仍能保持较好的估计性能.
1 系统模型假设存在这样一个宽带无线系统,系统信道在n时刻的有限脉冲响应为w=
| $ \mathit{\boldsymbol{y}}\left( n \right) = {\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{x}}\left( n \right) + \mathit{\boldsymbol{N}}\left( n \right) $ | (1) |
其中:导频信号x(n)=[x(n), x(n-1), …, x(n-N+1)]用于探测未知的信道向量;w为需要被预测的系统信道的N维列向量形式,研究表明,实际的多径信道在时域上具有分簇的特点[3],如图 1所示;N(n)为满足高斯混合模型的噪声信号,可以描述为
| $ p\left( {\mathit{\boldsymbol{N}}\left( n \right)} \right) = \left( {1 - \mathit{\varphi }} \right){\rm{CN}}\left( {0,\mathit{\sigma }_{{n_1}}^2} \right) + \mathit{\varphi }{\rm{CN}}\left( {0,\mathit{\sigma }_{{n_2}}^2} \right) $ | (2) |

|
图 1 多径信道分簇示意图 |
其中:CN(0,
| $ \mathit{\sigma }_n^2 = E\left( {{\mathit{\boldsymbol{N}}^2}\left( n \right)} \right) = \left( {1 - \mathit{\varphi }} \right)\mathit{\sigma }_{{n_1}}^2 + \mathit{\varphi \sigma }_{{n_2}}^2 $ | (3) |
当φ=0时,N(n)退化为高斯噪声.综上所述,自适应信道估计的目标就是根据接收到的y(n)以及x(n)得到信道参数的估计值w(n).
2 变步长符号算法 2.1 基于平滑梯度向量的变步长方法近年来,Li等[8]在综合比较了已有的多种变步长方法的基础上,提出了一种新的变步长方法,即通过平滑因子β(0 < β < 1) 进行加权平均得到梯度向量p(n):
| $\mathit{\boldsymbol{p}}\left( n \right) = \beta \mathit{\boldsymbol{p}}\left( {n - 1} \right) + \left( {1 - \beta } \right){\rm{sgn}}\left( {\mathit{\boldsymbol{e}}\left( n \right)} \right)\mathit{\boldsymbol{x}}\left( n \right)$ | (4) |
其中瞬时估计误差e(n)可以表示为
| $ \mathit{\boldsymbol{e}}\left( n \right) = \mathit{\boldsymbol{y}}\left( n \right) = {\mathit{\boldsymbol{w}}^{\rm{T}}}\left( n \right)\mathit{\boldsymbol{x}}\left( n \right) $ | (5) |
其中w(n)为在第n次迭代过程中对信道参数矩阵的估计值.从而,步长μv(n)可以表示为
| $ {\mathit{\mu }_v}\left( n \right) = \alpha {\mathit{\mu }_v}\left( {n - 1} \right) + {\mathit{\gamma }_s}{\left\| {\mathit{\boldsymbol{p}}\left( n \right)} \right\|^2} $ | (6) |
其中α、γs为定值参数.可以看出,步长μv(n)决定着算法的收敛速度,要使算法的收敛速度加快,则可以通过调节参数α、γs以及梯度向量p(n)来获得一个较大的步长值. p(n)通过以误差函数e(n)为自变量的符号函数来控制梯度向量收敛的正负极性,根据x(n)的取值大小来控制梯度向量p(n)收敛的幅值.因此,该算法可以在自适应迭代初期通过梯度向量获得较大的步长值来加快收敛速度,在自适应迭代稳定阶段调整p(n)获得较小的步长值来保证收敛的稳定性.为了进一步提高该方法的收敛速度,提出了一种基于混合范数的变步长方法.
2.2 基于混合范数的变步长符号算法首先,对式(4) 中的x(n)进行归一化得到
| $ \mathit{\boldsymbol{p}}\left( n \right) = \beta \mathit{\boldsymbol{P}}\left( {n - 1} \right) + \left( {1 - \beta } \right){\mathop{\rm sgn}} \left( {\mathit{\boldsymbol{e}}\left( n \right)} \right)\frac{{\mathit{\boldsymbol{x}}\left( n \right)}}{{\left\| {\mathit{\boldsymbol{x}}\left( n \right)} \right\|}} $ | (7) |
通过对梯度向量p(n)的二次范数与三次范数
形式进行加权求和,可以将式(6) 转化为
| $ {\mathit{\mu }_v}\left( n \right) = \alpha {\left\| {\mathit{\boldsymbol{p}}\left( n \right)} \right\|^2} + \mathit{\gamma }{\left\| {\mathit{\boldsymbol{p}}\left( n \right)} \right\|^3} $ | (8) |
即通过混合范数来使得步长μv(n)在迭代初期依靠梯度向量p(n)的三次范数来加快收敛速度;在迭代中后期,随着p(n)的减小,p(n)的二次范数将发挥更重要的作用.
在这种基于混合范数的变步长方法基础上,充分利用加权趋零的损耗函数在稀疏信道估计中的优点,与符号算法相结合,并采用改进的变步长方法,提出加权趋零混合范数变步长符号算法(RZA-MNVSS-SA, re-weighted zero-attracting mixed norm variable step-size sign algorithm),其迭代公式可以表示为
| $ \begin{array}{l} \mathit{\boldsymbol{\tilde w}}\left( {n + 1} \right) = \\ \mathit{\boldsymbol{\tilde w}}\left( n \right) + {\mathit{\mu }_v}\left( n \right){\mathop{\rm sgn}} \left( {\mathit{\boldsymbol{e}}\left( n \right)} \right)\mathit{\boldsymbol{x}}\left( n \right) - {\mathit{P}_{{\rm{RZA}}}}\left( n \right) \end{array} $ | (9) |
其中:
根据上一节的分析,所提出的基于梯度向量混合范数的变步长符号算法相较于传统的变步长NLMS算法在相同估计精度下具有更快的收敛速度,并且在冲击噪声环境下具有更好的稳健性.本节对相关算法在高斯白噪声以及冲击噪声下的性能以及当稀疏信道发生突变后的性能进行比较.算法性能由信道估计的均方偏差(MSD, mean square deviation)来衡量,即
| $ {\rm{MSD}}\left\{ {\mathit{\boldsymbol{w}}\left( n \right)} \right\} = E\left\{ {{{\left\| {\mathit{\boldsymbol{w}} - \mathit{\boldsymbol{w}}\left( n \right)} \right\|}^2}} \right\} $ | (10) |
其中:w和w(n)分别为实际信道参数矩阵以及对该信道第n次自适应信道估计值,‖·‖2表示2-范数.
仿真所用到的瑞利信道矩阵的长度L=16,稀疏度K=3,非零抽头的位置分别为1、9、13.导频信号x(n)通过四进制相移键控调制得到.噪声信号N(n)通过高斯混合模型生成,当混合度φ=0或φ=0.01时,分别表示所加噪声为高斯白噪声或包含高斯白噪声与冲击噪声的混合噪声;高斯白噪声的方差取值为
令混合度φ=0,使所加噪声为高斯白噪声,迭代次数N=1×104,仿真结果如图 2所示.
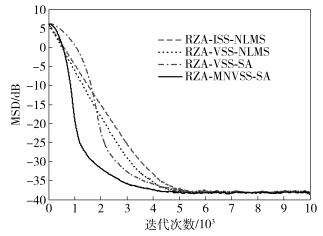
|
图 2 高斯白噪声下稀疏度为3的算法性能比较 |
由图 2可知,在环境噪声为高斯白噪声时,所提出的基于梯度向量混合范数变步长方法可以在迭代开始时通过‖p(n)‖2获得较大的步长值,加快算法的收敛速度;随着迭代的进行,梯度向量p(n)的值逐渐减小,‖p(n)‖2衰减较快,此时主要通过‖p(n)‖2获得一个适中的步长值以提高收敛精度.所以,图 2所示的4种算法在达到相同收敛精度的情况下,所提出算法的收敛速度快于其他3种算法.
令混合度取为φ=0.01,使所加噪声变为包含冲击噪声与高斯白噪声的混合噪声,其他参数保持不变,得到的仿真结果如图 3所示.
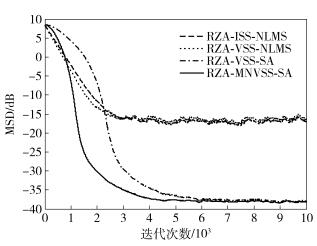
|
图 3 冲击噪声下稀疏度为3的算法性能比较 |
对比图 3与图 2可知,当所加噪声含有冲击噪声时,基于NLMS的算法由于其迭代公式中直接使用到的误差函数e(n)受到冲击噪声影响较大,从而使得信道估计精度受到极大的影响;而所提出的RZA-MNVSS-SA算法引入符号函数对e(n)进行处理,并且每次迭代中的梯度向量是由上次迭代的梯度向量与本次迭代的观测值加权求和得到,相当于进行了低通滤波处理,可以有效降低噪声对步长值的影响.因此,所提出的算法在冲击噪声中仍能保持较好的信道估计性能.
在自适应信道估计算法中,迭代公式中初始参数的选取对算法的性能有着较大的影响,因此还需要检验算法在信道参数发生改变而迭代公式中初始参数保持不变时的信道估计性能的稳定性.因此将总的迭代次数改为N=2×104,稀疏信道的稀疏度K=3保持不变,令前1×104次迭代时非零抽头的位置分别为1、9、13,令后1×104次迭代时非零抽头的位置分别为3、5、14,非零抽头的参数值也随之发生变化.在高斯白噪声环境下仿真结果如图 4所示.
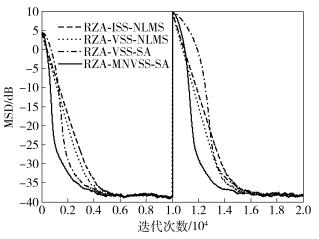
|
图 4 高斯白噪声下信道状态信息变化后的算法性能比较 |
由图 4可以看出,在前1×104次迭代时算法的性能与图 2所示的结果类似;当信道稀疏性发生改变时,由于所提出的变步长方法主要依靠梯度向量混合范数的加权平均确定步长值,对初始参数值选取的依赖性较小,所以仍能以较快的迭代速度使算法收敛.在冲击噪声环境下仿真结果如5所示.
对比图 5与图 4可以看出,在冲击噪声环境下,当信道状态信息发生突变时,所提出的算法仍然能保持较快的收敛速度.由图 4及图 5可知,所提出的算法在高斯白噪声及冲击噪声环境下均具有较强的追踪性能,即当信道状态信息发生突变时,能较快地恢复到最佳的信道估计精度.
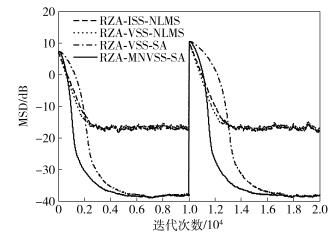
|
图 5 冲击噪声下信道状态信息变化后的算法性能比较 |
笔者以近年来对自适应稀疏信道估计算法的相关研究为基础,提出了加权趋零的梯度向量混合范数变步长符号算法.仿真结果表明,所提出的基于混合范数变步长符号算法相较于传统信道估计算法具有更快的收敛速度,在冲击噪声环境下仍能保持较好的信道估计性能,当信道参数发生变化时仍然能够在较短的时间内达到较好的信道估计精度.下一步将进一步研究变步长符号算法在大规模多输入多输出系统中稀疏信道估计的应用.
| [1] | Wang Weihua, Zhao Jihong, Qu Hua, et al. A switch kernel width method of correntropy for channel estimation[C]//International Joint Conference on Neural Networks.[S.l.]:IEEE, 2015:1-7. |
| [2] | Wang Weihua, Zhao Jihong, Qu Hua, et al. An adaptive kernel width update method of correntropy for channel estimation[C]//International Conference on Digital Signal Processing.[S.l.]:IEEE, 2015:916-920. |
| [3] | Bajwa W U, Haupt J, Raz G, et al. Compressed channel sensing[C]//Conference on Information Sciences and Systems 2008(CISS 2008).[S.l.]:[s.n.], 2008:5-10. |
| [4] | Gui Guan, Adachi F. Stable adaptive sparse filtering algorithms for estimating multiple-input-multiple-output channels[J]. IET Communications, 2014, 8(7): 1032–1040. doi: 10.1049/iet-com.2013.0665 |
| [5] | Gui Guan, Adachi F. Improved least mean square algorithm with application to adaptive sparse channel estimation[J]. Eurasip Journal on Wireless Communications & Networking, 2013, 2013(1): 1–18. |
| [6] | Chen Yilun, Gu Yuantao, Hero A O. Sparse LMS for system identification[C]//IEEE International Conference on Acoustics.[S.l.]:[s.n.], 2009:3125-3128. |
| [7] | Gui Guan, Xu Li, Shan Lin, et al. Adaptive MIMO channel estimation using sparse variable step-size NLMS algorithms[C]//IEEE International Conference on Communication Systems.[S.l.]:IEEE, 2014:605-609. |
| [8] | Li Yuanping, Lee T S, Wu Bingfei. A variable step-size sign algorithm for channel estimation[J]. Signal Processing, 2014, 102: 304–312. doi: 10.1016/j.sigpro.2014.03.030 |


