在路侧基础设施密集部署的车联网场景中,针对车载终端时延受限内容的下载需求,提出了一种调度算法.该算法基于李雅普诺夫优化方法,利用分组的等待时延建立李雅普诺夫方程,通过传输和丢包决策可以保证用户的时延需求,并保证系统稳定.仿真结果表明,相比于最早过期优先算法,提出的方法在满足用户时延需求的同时,进一步提升了系统的吞吐量.
A scheduling algorithm for the latency-constrained content dissemination in vehicular networks with dense deployment of Roadside Units was proposed based on Lyapunov optimization, which uses the explicit delay information from the head-of-line packet at each vehicle to stabilize the network. By proper scheduling and dropping packet, the network throughput is maximized while ensuring the delay requirement. Simulations show that the proposed algorithm can guarantee the demand of delay and improve the system throughput compared with the earliest expiration priority algorithm.
车联网技术的应用非常广泛,包括交通信息共享与智能驾驶,以及娱乐内容共享等[1].其中,车载终端的内容下载受到了广泛的关注,如车辆在运行过程中可以向服务器请求路况信息、娱乐信息等[2].为了提升车载终端的下载速率,可以通过密集部署路侧基础设施(RSU, road side unit)拉近终端和接入点之间的距离[3].然而,在RSU密集部署的场景中,相邻RSU干扰严重,车载终端运动速度快,传输速率会随着车辆的移动显著变化,因此,需要研究一种适应于该场景的内容下载调度算法.
针对车联网场景中的内容下载问题,彭军等[4]提出了车辆间协作从RSU下载内容的方案,这种方式适用于RSU稀疏部署,车辆有可能处在覆盖范围之外的情况. Ding等[5]提出了一种缓存方法,RSU预先缓存一些受欢迎的内容,这样可以减少内容下载时间,提高内容下载效率.
笔者考虑RSU密集部署的车联网场景中,车辆请求时延受限的内容传输方法,即车辆请求下载的内容有一个有效的期限[6],服务器需要在有效期内把内容传输给车辆,否则内容失效.最大速率优先算法总是调度当前信道条件最好的车辆[7],即优先调度数据速率最高的车辆,这种方法不适用于时延受限内容的下载.最早过期优先(EDD, earliest due date)算法优先调度最先过期的数据包,该机制不能最大化系统的吞吐量,因为有些数据包可能是以非常低的传输速率调度的[8].综上所述,研究一种高效的时延受限的内容调度方法是非常重要的.
笔者依据李雅普诺夫优化方法,利用分组的等待时延建立李雅普诺夫方程,保证系统稳定,在满足时延限制需求的同时,进一步提升系统的吞吐量.
1 系统模型与问题描述 1.1 系统模型在M个RSU密集部署的场景下,假设系统中共有V辆车随机请求下载内容,服务器为每辆车维持一个队列Qv,因此系统中共有V个队列.令向量A(t)=(A1(t), A2(t), …, AV(t))表示请求到达过程,即Av(t)表示时隙t到达队列Qv的分组数.假设A(t)是独立同分布的伯努利过程,其期望为E{A(t)}=λ,其中λ
| $ {Q_v}\left( {t + 1} \right) = \max \left[ {{Q_v}\left( t \right) - {\mu _v}\left( t \right) - {D_v}\left( t \right),0} \right] + {A_v}\left( t \right) $ | (1) |
其中:
令向量Sj(t)=(Sj1(t), Sj2(t), …, SjV(t))表示t时刻RSUj到所有车辆的传输速率,即Sjv(t)表示t时刻RSUj可以成功为车辆v传输的分组数.令向量xj(t)=(xj1(t), xj2(t), …, xjV(t))表示RSUj的调度动作向量,其中xjv(t)∈{0, 1},xjv(t)=1表示RSUj在t时隙给车辆v传输,如果限制每个RSU在同一时隙只能调度一辆车,那么向量xj(t)中最多只有一个分量为1.令χ表示所有可行的x(t)的集合.因此,μv(t)可表示为
| $ {\mu _v}\left( t \right) = \sum\limits_{j = 1}^M {{\mu _{jv}}\left( t \right) = \sum\limits_{j = 1}^M {{x_{jv}}\left( t \right){S_{jv}}\left( t \right)} } $ | (2) |
目标是满足用户时延需求的同时,提升系统的吞吐量性能.定义向量Y(t)=(Y1(t), Y2(t), …, YV(t))表示系统的吞吐量,即Yv(t)表示时隙t队列Qv的吞吐量,定义为
| ${Y_v}(t) \buildrel \Delta \over = {\lambda _v} - {D_v}(t)$ | (3) |
定义变量yv(t)表示Yv(t)的时间均值,即
| $ g\left( {\bf{ \pmb{\mathsf{ γ}} }} \right) = \sum\limits_{v = 1}^V {\left( {1{\rm{g}}\left( {1 + \max \left[ {{\gamma _v},0} \right]} \right) + \min \left[ {{\gamma _v},0} \right]} \right)} $ | (4) |
目标是最大化系统吞吐量,同时要保证用户的时延需求,最优化问题可以表述为
| $ \max :g\left( {\mathit{\boldsymbol{\bar \gamma }}} \right) $ | (5) |
| $ {\rm{s}}.{\rm{t}}.{{\bar Q}_v} < \infty ,v \in \left\{ {1,2, \cdots ,V} \right\} $ | (6) |
| $ {{\bar y}_v} \geqslant {{\bar \gamma }_{\rm{v}}},v \in \left\{ {1,2, \cdots ,V} \right\} $ | (7) |
| $ - 1 \leqslant {\gamma _{\rm{v}}}\left( t \right) \leqslant 1,v \in \left\{ {1,2, \cdots ,V} \right\} $ | (8) |
| $ \mathit{\boldsymbol{\bar Q}}和\mathit{\boldsymbol{\bar y}}\mathit{可确定} $ | (9) |
其中:向量Q={Q1, Q2, …, QV}表示系统队列平均长度,
| $ {Z_v}\left( {t + 1} \right) = \max \left[ {{Z_v}\left( t \right) - {\lambda _v} + {D_v}\left( t \right) + {\gamma _v}\left( t \right),0} \right] $ | (10) |
把Yv(t)的定义式(3) 代入式(10),并对τ∈{0, 1, …, t-1}累加求和再除以t可得
| $ \frac{{{Z_v}\left( t \right) - {Z_v}\left( 0 \right)}}{t} + \frac{1}{t}\sum\limits_{\tau = 0}^{t - 1} {{Y_v}\left( \tau \right) \geqslant } \frac{1}{t}\sum\limits_{\tau = 0}^{t - 1} {{\gamma _v}\left( \tau \right)} $ | (11) |
对不等式(11) 两边求期望,且Zv(0)=0,进一步可得
| $ \frac{{E\left\{ {{Z_v}\left( t \right)} \right\}}}{t} + {{\bar y}_v}\left( t \right) \geqslant {{\bar \gamma }_{\rm{v}}}\left( t \right) $ | (12) |
由式(12) 可知,如果E{Zv(t)}/t→0,即虚拟队列Zv(t)稳定,则约束条件(7) 成立.
1.3 分组等待时延的计算每个时隙,服务器首先决定调度变量,如果服务器决定调度队列Qv,则Qv中至少有一个分组被传输,如果队列Qv没有被调度,再根据时延决定是否要丢包.
令Hv(t)表示时隙t队列Qv队首分组的等待时延,如果队列Qv为空,则Hv(t)=0.如果在时隙t,有一个分组到达空队Qv,则该分组在t+1时隙才会变成队首分组,并设该分组的等待时延Hv(t+1)=1.定义指示变量αv(t),如果队列Qv(t)不为空,则αv(t)=1;否则αv(t)=0,则时延Hv(t)可按式(13) 计算.
| $ \begin{array}{*{20}{c}} {{H_v}\left( {t + 1} \right) = } \\ {{\alpha _v}\left( t \right)\max \left[ {{H_v}\left( t \right) + 1 - \left( {{\mu _v}\left( t \right) + } \right.} \right.} \\ {\left. {\left. {{D_v}\left( t \right)} \right){T_v}\left( t \right),0} \right] + \left( {1 - {\alpha _v}\left( t \right)} \right){A_v}\left( t \right)} \end{array} $ | (13) |
其中Tv(t)为连续2个分组到达的时间间隔.由式(13) 可知,当αv(t)=0时,即队列Qv为空,如果时隙t有分组到达,则Hv(t+1)=1.如果队首的分组既没有被传输也没有被丢弃,即μv(t)+Dv(t)=0,那么时延Hv(t)加1;否则,队首分组成功传输或者被丢弃,则后面的分组变成队首分组,时延为max[Hv(t)+1-(μv(t)+Dv(t))Tv(t), 0].
2 提出的调度算法 2.1 李雅普诺夫优化方法根据李雅普诺夫优化方法可知,可以依据系统队列长度设计调度算法来保证系统的稳定性并最大化系统的吞吐量[9].由式(13) 可知,对于所有的v∈{1, 2, …, V},队列长度总是小于等于该队首分组的等待时延,即Qv(t)≤Hv(t)成立,因此利用H(t)代替Q(t)设计调度方法来保证系统的稳定性,即保证H(t)有界,这样就可以满足时延要求,同时也保证了Q(t)有界,吞吐量最大.另外,为了满足约束条件(7),需要保证虚拟队列Z(t)稳定.因此,定义Θ(t) [Z(t); H(t)]作为队列Z(t)和H(t)的联合向量,不失一般性,假设λv>0,定义李雅普诺夫方程为
| $ L\left( {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}\left( t \right)} \right) = \frac{1}{2}\sum\limits_{v = 1}^V {Z_v^2} \left( t \right) + \frac{1}{2}\sum\limits_{v = 1}^V {{\lambda _v}} H_v^2\left( t \right) $ | (14) |
相应地,李雅普诺夫方程的偏移量Δ(Θ(t))可以表述为
| $\Delta \left( {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}\left( t \right)} \right) = E\left\{ {L\left( {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}\left( {t + 1} \right)} \right) - L\left( {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}\left( t \right)} \right)\left| {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}\left( t \right)} \right.} \right\}$ | (15) |
根据李雅普诺夫优化方法中的偏移加罚模型[10],每个时隙,算法应最小化边界值:
| $ \min \Delta \left( {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}\left( t \right)} \right) - {D_{\max }}E\left\{ {g\left( {\mathit{\boldsymbol{\gamma }}\left( t \right)} \right)\left| {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}\left( t \right)} \right.} \right\} $ | (16) |
其中:Δ(Θ(t))代表队列的稳定情况;g(γ(t))代表优化的目标,也就是系统吞吐量;Dmax是一个非负权重,用来影响性能的折中,这里Dmax是给定的,表示内容的最大时延要求,如果时延要求较小,则很多包会被丢弃,系统吞吐量下降,因此,该值的大小会影响系统性能.
根据李雅普诺夫方程的定义,可以得到下面2个定理,由于篇幅的限制,证明过程省略.
定理1 每个时隙t,对于任意的Θ(t),采用任意一种调度算法,李雅普诺夫方程偏移量满足
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}\left( {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}\left( t \right)} \right) \leqslant B - \sum\limits_v {{Z_v}} \left( t \right)E\left\{ {{Y_v}\left( t \right) - } \right.} \\ {\left. {{\gamma _v}\left( t \right)\left| {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}\left( t \right)} \right.} \right\} - \sum\limits_v {{\lambda _v}} {H_v}E\left\{ {\left( {{\mu _v}\left( t \right) + } \right.} \right.} \\ {\left. {\left. {{D_v}\left( t \right)} \right){T_v}\left( t \right) - 1\left| {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}\left( t \right)} \right.} \right\}} \end{array} $ | (17) |
其中B为常数.
定理2 每个时隙t,对于任意的Θ(t),采用任意一种调度算法,Tv(t)与Dv(t)、μv(t)和Θ(t)相互独立,可得
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{ \boldsymbol{\varDelta} \boldsymbol{\varTheta} }}\left( t \right) - {D_{\max }}E\left\{ {g\left( {\mathit{\boldsymbol{\gamma }}\left( t \right)} \right)\left| {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}\left( t \right)} \right.} \right\} \leqslant } \\ {B - {D_{\max }}E\left\{ {g\left( {\mathit{\boldsymbol{\gamma }}\left( t \right)} \right)\left| {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}\left( t \right)} \right.} \right\} - } \\ {\sum\limits_v {{Z_v}\left( t \right)E\left\{ {{\lambda _v} - {D_v}\left( t \right) - {\gamma _v}\left( t \right)\left| {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}\left( t \right)} \right.} \right\} - } } \\ {\sum\limits_v {{H_v}\left( t \right)E\left\{ {{\mu _v}\left( t \right) + {D_v}\left( t \right) - {\lambda _v}\left| {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}\left( t \right)} \right.} \right\}} } \end{array} $ | (18) |
其中B的值与定理1相同.
因为假设请求到达Av(t)是伯努利过程,所以到达间隔Tv(t)是均值为E{Tv(t)}=1/λv的几何过程.
2.2 算法步骤本节给出算法的具体步骤.根据定理1和定理2,最小化目标变成式(18) 中不等号的右边项.
每个时隙t,服务器根据Z(t)、H(t)和S(t)的值,通过决策控制变量γ(t)、D(t)、x(t)来最小化式(18) 中不等号的右边项,整理式(18) 中包括控制变量的项可得
| $ \begin{array}{*{20}{c}} {{D_{\max }}E\left\{ {g\left( {\mathit{\boldsymbol{\gamma }}\left( t \right)} \right)\left| {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}\left( t \right)} \right.} \right\} - } \\ {\sum\limits_{v = 1}^V {{Z_v}\left( t \right)E\left\{ {{D_v}\left( t \right) + {\gamma _v}\left( t \right)\left| {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}\left( t \right)} \right.} \right\}} + } \\ {\sum\limits_{v = 1}^V {{H_v}\left( t \right)E\left\{ {\left( {{\mu _v}\left( t \right) + {D_v}\left( t \right)} \right)\left| {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}\left( t \right)} \right.} \right\}} } \end{array} $ | (19) |
1) 选择辅助变量:γ(t)={γ1(t), γ2(t), …, γV(t)},每个时隙根据Θ(t)的值,通过求解下列问题,可得γ(t).
| $ \max :{D_{\max }}g\left( {\gamma \left( t \right)} \right) - \sum\limits_{v = 1}^V {{Z_v}\left( t \right)} {\gamma _v}\left( t \right) $ | (20) |
| $ {\rm{s}}{\rm{.t}}. - 1 \leqslant {\gamma _v}\left( t \right) \leqslant 1,v \in \left\{ {1,2, \cdots ,V} \right\} $ | (21) |
变量γ(t)的值影响队列Z(t)的更新,从而影响D(t)的值.
2) 选择传输变量:现在考虑服务器如何为RSUj选择传输动作向量xj(t)=(xj1(t), xj2(t), …, xjV(t)),其中变量xjv(t)∈{0, 1},重新整理式(19) 中的剩余项可得
| $ \begin{array}{*{20}{c}} {\sum\limits_{v = 1}^V {{H_v}\left( t \right)E\left\{ {{\mu _v}\left( t \right)\left| {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}\left( t \right)} \right.} \right\}} + } \\ {\sum\limits_{v = 1}^V {\left( {{H_v}\left( t \right) - {Z_v}\left( t \right)} \right)E\left\{ {{D_v}\left( t \right)\left| {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}\left( t \right)} \right.} \right\}} } \end{array} $ | (22) |
定义一个标志变量mv(t),当Hv(t)≥Zv(t)时,mv(t)=1;否则mv(t)=0.假设如果服务器调度了队列Qv,则至少可成功传输一个分组,服务器就不会再丢包,因此,如果服务器没有调度队列Qv,且mv(t)=1时,则Dv(t)=1,再由式(2) 可知,
| $ \begin{array}{*{20}{c}} {\sum\limits_{v = 1}^V {{H_v}\left( t \right){\mu _v}\left( t \right) + \sum\limits_{v = 1}^V {\left( {{H_v}\left( t \right) - {Z_v}\left( t \right)} \right){D_v}\left( t \right)} } = } \\ {\sum\limits_{v = 1}^V {{H_v}\left( t \right)\sum\limits_{j = 1}^M {{x_{jv}}\left( t \right){S_{jv}}\left( t \right) + \sum\limits_{v = 1}^V {{D_v}\left( t \right)\left( {{H_v}\left( t \right) - } \right.} } } } \\ {\left. {{Z_v}\left( t \right)} \right)\left( {1 - \sum\limits_{j = 1}^M {{x_{jv}}\left( t \right)} } \right){m_v}\left( t \right)} \end{array} $ | (23) |
整理式(23),只考虑包含控制变量的项,可得
| $ \begin{array}{*{20}{c}} {\max :\sum\limits_{v = 1}^V {{H_v}\left( t \right)\sum\limits_{j = 1}^M {{x_{jv}}} \left( t \right){S_{jv}}\left( t \right)} - }\\ {\sum\limits_{v = 1}^V {{m_v}\left( t \right)\left( {{H_v}\left( t \right) - {Z_v}\left( t \right)} \right)} \sum\limits_{j = 1}^M {{x_{jv}}\left( t \right)} } \end{array} $ | (24) |
| $ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\;\;\;\mathit{\boldsymbol{x}}\left( t \right) \in \mathit{\boldsymbol{\chi }} $ | (25) |
根据S(t)和Θ(t)的值最大化式(24) 求x(t).
3) 丢包决策:如果队列Qv的队首分组没有被调度,且满足Zv(t)≤Hv(t),则丢掉队首分组,即Dv(t)=1.
求出变量γ(t)后,要最大化表达式:
| $ \sum\limits_v {{H_v}\left( t \right){\mu _v}\left( t \right)} + \sum\limits_v {\left( {{H_v}\left( t \right) - {Z_v}\left( t \right)} \right)} {D_v}\left( t \right) $ |
因此当Zv(t)≤Hv(t)时,应令Dv(t)=1,即队列Qv丢包.
4) 队列更新:利用上述过程给出的控制变量γv(t)和Dv(t)的值更新虚拟队列Zv(t).同时,根据队首分组是否传输成功,更新队列Qv(t)和队首分组的时延Hv(t).
2.3 时延分析根据算法步骤1) 求解变量γv(t)时,如果满足Zv(t)>Dmax,则γv(t)=-1,由于Dv(t)≤1,所以此时γv(t)+Dv(t)≤0,根据Zv(t)的更新公式(10),Zv(t+1)≤Dmax,即该算法可以保证Zv(t)有上界.
下面分析提出的算法可以满足时延需求.对于任意队列Qv(t),首先在t=0时,队列为空,时延Hv(t)=0.然后,假设时隙t,时延满足Hv(t)≤Dmax-1,由时延更新公式(13) 可知,从时隙t到t+1最多增加1,所以,Hv(t+1)≤Dmax;反之,如果Hv(t)>Dmax-1,因为时延Hv(t)是整数,则Hv(t)=Dmax,又因为Zv(t)≤Dmax,所以此时Hv(t)≥Zv(t)成立,如果服务器没有调度队列Qv(t),根据算法步骤3) 丢包决策可得Dv(t)=1,此时Qv(t)的队首分组会被丢弃.因此,该算法可以保证时延的上界是Dmax.
3 仿真 3.1 仿真参数设置在仿真中首先使用VISSIM软件模拟车辆的运行过程[11],记录每个时隙车辆的位置信息.考虑直线型的高速场景,公路长度设为1 km.车辆由两端入口进入,到达过程服从泊松分布,达到率θ设为300车/h/入口.另外,车速在90~120 km/h之间变化. RSU密集部署,间距200 m,假设系统中共有3辆车.车辆的请求过程相互独立,服从参数为λv的伯努利分布.其他参数如表 1所示.
根据式(3) 给出的吞吐量的定义,在仿真中,通过统计车辆请求的包数和被丢弃的包数可以确定系统的平均吞吐率.
|
|
表 1 仿真参数 |
图 1所示为基于提出的算法和EDD算法下,系统吞吐量和请求到达率的关系.结果表明,当平均到达率小于0.3时,2种算法的吞吐量性能一样,都是最优的;当到达率大于0.3时,提出的算法性能优于EDD算法.
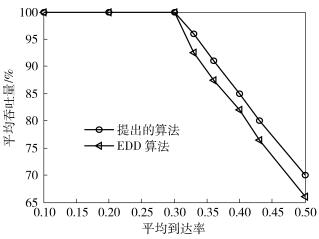
|
图 1 吞吐量随到达率的变化 |
图 2所示为基于提出的算法和EDD算法下平均等待时延和请求到达率的关系,其中Dmax是给定的时延要求. 图 2结果表明,采用提出的算法平均等待时延小于采用EDD算法的时延,当到达率较大时,即系统负荷重时,提出的算法仍然可以保证时延满足要求,而EDD算法的时延不满足要求.
图 3所示为基于提出的算法和EDD算法下系统丢包率和时延的关系.当Dmax值较小时,采用2种算法系统的丢包率都很高,但是提出的算法明显优于EDD算法;当时延Dmax增大时,丢包率明显下降;当时延很大时,丢包率的变化不再明显,因为所有数据包都有足够的时间可以被调度.
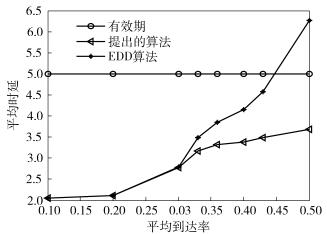
|
图 2 时延随到达率的变化 |
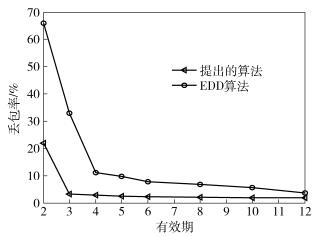
|
图 3 丢包率随时延的变化 |
提出了在密集部署RSU的车联网场景下,时延受限内容传输调度算法,利用分组的等待时延建立李雅普诺夫方程,保证系统稳定,最大化吞吐量的同时保证分组等待时延有界.仿真结果表明,相比于现有的算法,提出的算法可以保证时延需求,进一步提升了系统吞吐量性能.
| [1] |
李静林, 刘志晗, 杨放春. 车联网体系结构及其关键技术[J]. 北京邮电大学学报, 2014, 37(6): 95–100.
Li Jinglin, Liu Zhihan, Yang Fangchun. Internet of vehicles:the framework and key technology[J]. Journal of Beijing University of Posts and Telecommunications, 2014, 37(6): 95–100. |
| [2] | Malandrino F, Casetti C, Chiasserini C, et al. Content download in vehicular networks in presence of noisy mobility prediction[J]. IEEE Transactions on Mobile Computing, 2014, 13(5): 1007–1021. doi: 10.1109/TMC.2013.128 |
| [3] | Huang Pohan, Psounis K. Efficient mmwave wireless backhauling for dense small-cell deployments topology[C]//Annual Conference on Wireless On-demand Network Systems and Services (WONS). Jackson:IEEE, 2017:88-95. |
| [4] |
彭军, 马东, 刘凯阳, 等. 基于LTE D2D技术的车联网通信架构与数据分发策略研究[J]. 通信学报, 2016, 37(7): 62–70.
Peng Jun, Ma Dong, Liu Kaiyang, et al. LTE D2D based vehicle networking communication architecture and data distributing strategy[J]. Journal on Communications, 2016, 37(7): 62–70. |
| [5] | Ding Ruizhou, Wang Tianyu, Song Lingyang, et al. Roadside-unit caching in vehicular ad hoc networks for efficient popular content delivery[C]//IEEE Wireless Communications and Networking Conference. New Orleans:IEEE Press, 2015:1207-1212. |
| [6] | Giannini C, Calegari P, Buratti C, et al. Delay tolerant network for smart city:exploiting bus mobility[C]//2016 IEEE Aeit International Annual Conference (AEIT). Naples:IEEE Press, 2016:1-6. |
| [7] | Yang Shengbo, Yeo C K, Lee B S. MaxCD:maxrate based cooperative downloading for drive-thru networks[C]//International Conference on Computer Communications and Networks. Munich:IEEE Press, 2012:1-7. |
| [8] | Elhadad M, El-Rabaie E, Abd-Elnaby M. Resource allocation for real-time services using earliest due date mechanism in LTE networks[C]//International Japan-Egypt Conference on Electronics Communications and Computers (JEC-ECC). Cario:IEEE Press, 2016:9-12. |
| [9] | Georgiadis L, Neely M J, Tassiulas L. Resource allocation and cross-layer control in wireless networks[J]. Foundations and Trends in Networking, 2006, 1(1): 1–149. doi: 10.1561/1700000002 |
| [10] | Neely M J. Delay-based network utility maximization[J]. IEEE/ACM Transactions on Networking, 2013, 21(1): 41–54. doi: 10.1109/TNET.2012.2191157 |
| [11] | Zhou Haibo, Liu Bo, Tom H Luan, et al. ChainCluster:engineering a cooperative content distribution framework for highway vehicular communications[J]. IEEE Transactions on Intelligent Transportation System, 2014, 15(6): 2644–2657. doi: 10.1109/TITS.2014.2321293 |


