2. 广西信息科学实验中心, 桂林 541004;
3. 广西可信软件重点实验室, 桂林 541004
针对现有智能家居入侵检测算法收敛速度慢及抗干扰能力差进而导致决策系统实时性和鲁棒性差的缺陷,分析了时空域证据融合的特性,得出时域融合存在冲突融合、空域融合更存在去除冲突融合的结论.基于此,提出了基于证据理论的时域自适应加权算法及空域证据修正的3种证据融合入侵检测算法,并将提出的检测算法应用于智能家居入侵检测系统.检测结果表明,提出的算法能够加快融合结果的收敛速度,增强抗干扰能力,并能提高入侵检测系统决策的实时性和鲁棒性.
2. Guangxi Information Science Research Centre, Guilin 541004, China;
3. Guangxi Key Laboratory of Trusted Software, Guilin 541004, China
The existing smart home intrusion detection algorithm has the defects of slow convergence speed and weak anti-interference ability which can weaken the real-time and robustness of decision-making system. By analyzing the characteristics of time domain data and spatial domain evidence, it is concluded that the temporal fusion is focused more on conflict data but more attention is paid to remove conflict data fusion in the spatial domain. Therefore, an adaptive weighted algorithm for temporal fusion and three evidence fusion intrusion detection solution based on modified evidence were proposed. Further analysis is done by applying the algorithm in intelligent house intrusion detection system. Simulations verify that the fusion result of new proposed algorithms not only accelerate the convergence rate and enhance anti-jamming capability comparing with existing algorithms, but also improve the real-time and robustness of intrusion detection system decision-making.
在传统的家居安防领域,单一的传感器难以实现对入侵的准确检测,利用多传感器的信息融合可以提高入侵检测的实时性和准确性.当前,传感器的信息融合研究多集中在多传感器间的融合和单传感器多周期的融合上,并取得了很多研究成果[1-8],然而,对于多传感器多周期的时空域信息融合研究还不够深入. Hong等[9]较早地研究了基于Dempster-Shafer(D-S)证据理论的时空信息融合模型,总结了递归集中式结构和递归分布式结构的特点,但是其并未对高度冲突的证据进行处理,因而降低了D-S融合规则的有效性,并使得融合结果存在“一票否决”的缺陷,进而导致了决策系统缺乏鲁棒性而无法广泛应用. Yun等[10]在文献[9]的基础上将递归集中式结构和递归分布式结构应用于车辆的识别,在证据冲突程度不是很高的情况下取得了不错的效果,可是当证据间冲突程度很高时,其鲁棒性不足的缺陷逐渐显露.罗大庸等[11]提出了基于证据理论和模糊积分方法的信息融合算法,该算法主要用于目标检测,可是其检测的准确率依赖于检测的次数多少,这就使得时域融合在后续有利证据很少的情况下,收敛速度很慢,极大地影响了检测系统的实时性. Weeraddana等[12]在文献[13]的基础上提出了一种基于D-S信息过滤框架的时空域证据过滤器,引入了空间状态模型,采用加权滤波的方式削弱了干扰信息对融合结果的影响,并在火灾蔓延预测的应用中取得了不错的效果,但由于其本质是基于信任函数的加权融合,而权值由人为主观设定,因此其合理性不够且不利于推广到其他领域.
为了更好地发挥D-S规则以实现入侵检测,笔者在文献[8]和文献[12]的基础上将时域及空域下的融合拓展至时空二维,通过采用时域和空域的证据融合方法,构造基于证据理论的时空域信息融合模型,并进行了入侵检测仿真,验证了所提方法的可行性.
1 D-S理论及证据相关性度量方法 1.1 D-S证据理论基本概念[14-15]D-S证据理论用“识别框架Θ”表示所感兴趣的命题集{H1, H2, …, HN},它定义了一个幂集函数m:2Θ→[0, 1]且满足
| $\left. {\begin{array}{*{20}{c}} {m(\emptyset ) = 0}\\ {\sum\limits_{{H_i} \subseteq \Theta } {m({H_i}) = 1,i = 1,2, \cdots ,N} } \end{array}} \right\}$ | (1) |
则称m(Hi)为Hi的基本概率赋值函数或识别框架Θ上的基本可信度分配.基本可信度表征的是证据对焦元Hi本身的可信度大小.
D-S组合规则:假设mi表示识别框架Θ下第i组证据的概率分配函数,i=1, 2, …, N为证据的组数.那么,对于2组证据m1和m2的概率分配函数,用符号“⊕”来表示用D-S组合规则对其进行组合,即有
| $m(A) = {m_1} \oplus {m_2}(A) = \frac{1}{{1 - K}}\sum\limits_{{H_i} \cap {H_j} = A} {{m_1}({H_i}){m_2}} ({H_j})$ | (2) |
其中
时空域融合会对不同相关性的证据进行不同的处理,而经典D-S理论中的冲突系数K并不能很好地表征证据相关性[8].因此,为了更好地表征证据在时空域的融合,采用文献[8]中的方法来表征证据相关性,具体定义如下.
定义1[3-4] 单子集下的Pignistic概率函数.设Θ={H1, H2, …, HN}为识别框架,系统有N条相互独立的证据.识别框架Θ下的一条证据的焦元为Ak,则称
| ${\rm{Bet}}{P_m}({H_i}){\rm{ }} = \sum\limits_{{H_i} \in {A_k}} {\frac{1}{{|{A_k}|}}} m({A_k}),i = {\rm{ }}1,2, \cdots ,N$ | (3) |
为单子集Hi在基本概率赋值函数m下的Pignistic概率函数.经过Pignistic概率转换,它的基本概率赋值函数m′可以表示为
| ${m^′}{\rm{ = (Bet}}{P_m}({H_1}),{\rm{Bet}}{P_m}({H_2}), \cdots {\rm{Bet}}{P_m}({H_N}))$ | (4) |
定义2[8] 假定证据E1和E2经基础概率赋值函数Pignistic变换后为
| ${\rm{Sim}}({E_1},{E_2}) = \\\frac{{\sum\limits_{i = 1}^N {m_1^′({H_i}){\rm{ }}m_2^′({H_i})} }}{{\sum\limits_{i = 1}^N {m_1^′{{({H_i})}^2}{\rm{ + }}\sum\limits_{i = 1}^N {m_2^′{{({H_i})}^2} - \sum\limits_{i = 1}^N {m_1^′({H_i}){\rm{ }}m_2^′({H_i})} {\rm{ }}} } }}$ | (5) |
其中,相关性测度的取值范围为[0, 1],取值越大表明2个证据之间相关性就越大.
2 时空域信息融合入侵检测模型 2.1 基本思路入侵检测的目的是合理表征非法入侵者入侵前后的信息,入侵前后对传感器而言是2个完全冲突的过程,因此实现此目的的关键是明确时域和空域的证据中所表征的环境状态.时域证据表征的是变化的发生,而空域证据表征的是变化的程度,根据它们所表征的信息本质上的不同,可以确定它们的融合过程也不同,需要分别进行相应处理.基于此,提出了一种时空域信息融合入侵检测模型.
2.2 入侵检测模型时空域信息融合入侵检测模型如图 1所示,共分为3级,第1级为时域信息融合,第2级为空域信息融合,第3级为入侵决策级.
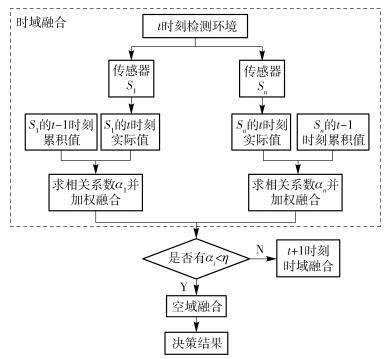
|
图 1 时空域融合入侵检测模型 |
第1级时域信息融合的关键在于既要表征时域证据在持续稳定环境中的关联性,又要表征其在骤然变化环境中的冲突性.为了达到这一目的,利用相关性系数为权值,加权融合时域证据.当环境处于相对稳定时,任何微小的变化都会因为加权操作而被削弱,使得融合结果更加平缓;当环境处于骤然变化时,冲突证据会进一步增强,融合结果更加突出变化的过程.为了降低网络中传感器节点的能源消耗,检测模型假设仅当实时证据与历史累积证据的相关性系数αi小于给定阈值η时,才触发空域融合.
第2级空域信息融合的关键在于表征证据之间的共性,即要把相关的证据保留下来,把不相关的信息排除出去.为了达到这一目的,就必须对冲突证据有一个很好的表征,准确识别不同原因造成的冲突证据,将其修正或去除.这样才能保证融合收敛的速度和检测结果的准确性.
第3级是决策级,最终决策的结果是根据空域融合结果与给定阈值进行比较,判定出当前是否遭到入侵.
3 时空域信息融合入侵检测方法 3.1 时域融合方法在实际应用中,所要检测的环境状态处于不断发展和变化中,当检测环境发生巨烈变化时,不同时刻采集到的传感器证据会产生较大冲突,时域上表现为证据之间弱相关性.若仅仅采用文献[12]的方法,为时域融合证据分配固定的权值,那么前后时刻信息完全矛盾的情况下,将不可能得到当前环境状态的客观描述.因此,如何分配合理的权值是表征时域信息关联性的关键.基于这一思想,为了客观合理地表征时域证据之间的关联性,笔者改进了文献[4]中的融合算法,提出了时域上采用自适应加权的时域融合方法,如方法1所示.
方法1 假定传感器Si在t时刻的基本可信度分配为mSi, t, p,在t-1时刻的累积可信度分配为mSi, t-1, c,则其在t时刻的累积可信度和融合得到的结果通过差分方程
| ${m_{{S_i},t,c}}(A) = {\alpha _{{S_i},t,t - 1}}{m_{{S_i},t - 1,c}}(A) + {\beta _{{S_i},t,t - 1}}{m_{{S_i},t,p}}(A)$ | (6) |
算得,则称传感器Si中的命题A在时域下的融合结果为mSi, t, c(A),其中αSi, t, t-1=Sim(ESi, t, p, ESi, t-1, c)为传感器Si在t时刻的实时证据与t-1时刻的累积证据的相关性系数,βSi, t, t-1=1-Sim(ESi, t, p, ESi, t-1, c)为传感器Si在t时刻的实时证据与t-1时刻的累积证据的冲突性系数.
3.2 空域融合方法与时域融合不同,空域融合更注重的是融合证据之间的关联性,具有强关联性的证据是对客观环境的一致性表征,而弱关联性证据很可能是因为自身故障或外界干扰、不同传感器精度不同等原因而产生的误差.如果将弱关联性证据不加处理就融合,不仅会影响证据融合的收敛速度,甚至还可能产生与事实相悖的结果,因此检测出弱相关性证据是解决该问题的关键.基于此,提出3种空域融合方案,3种方案检测环境相同,均满足在同一识别框架Θ下,有n个传感器S1, S2, …, Sn,且在同一时刻的累积证据记为E1, E2, …, En,对应的基本可信度分配为mS1, mS2, …, mSn. 3种方案中提到的相关概念定义见下文.
定义3 环形证据序列:假定证据E1, E2, …, En为由1到n按顺序排列的n个证据,则将证据E1和En首位相连,构成一个环,即称为环形证据序列.
定义4 证据Ei的权重ωi:环形序列中,任意证据Ei在所有证据中所拥有的权重ωi为
| ${\omega _i} = \frac{{{\rm{Sup}}({E_i})}}{{\sum\limits_{j = 1}^n {({E_j})} }},i = 1,2, \cdots ,n$ | (7) |
定义5 最弱相关性证据:若环形证据序列中,任意给定证据Ei与其在环中前一证据Ei-1和后一证据Ei+1的相关性Sim(Ei-1, Ei)和Sim(Ei, Ei+1)是所有证据中最小的,则称Ei为最弱相关性证据.
定义6 弱相关性证据:给定一个尽量小的阈值ηEIR,在环形证据序列中,任意证据Ei与其前一证据Ei-1和后一证据Ei+1的相关性Sim(Ei-1, Ei)和Sim(Ei, Ei+1)均小于ηEIR,则称Ei为弱相关性证据.
定义7 强相关性证据:给定一个尽量大的阈值ηER,在环形证据序列中,任意证据Ei与其前一证据Ei-1和后一证据Ei+1的相关性Sim(Ei-1, Ei)和Sim(Ei, Ei+1)均大于ηER,则称Ei为强相关性证据.
定义8 一般相关性证据:环形证据序列中,去除弱相关性证据和强相关性证据之后剩下的证据均称为一般相关性证据.
3.2.1 方案1:修正最弱相关性证据多传感器融合可以提高入侵检测的精度和准确率,但是由于干扰或故障的原因会产生最弱相关性证据,进而影响D-S融合的最终结果.基于此,提出用证据集期望值修正证据集中最弱相关性证据的空域融合方案,以减少最弱相关性证据对后续融合收敛速率的影响,进而保证D-S融合规则的有效性.具体步骤如下.
步骤1 计算出任意2条证据之间的相关性Sim(Ei, Ej),其中i, j=1, 2, …, n, 且i≠j.
步骤2 计算出每一条证据在所有证据中所占有的权值ωi.
步骤3 计算出证据集期望E,记为
| $\overline {E({A_i})} = \sum\limits_{j = 1}^n {{\omega _j}{m_j}({A_i}),} {A_i} \in \Theta $ | (8) |
步骤4 计算找到最弱相关性证据,记为Emin.
步骤5 用E替换Emin,以此来修正现有证据集合{E},形成新的证据集合{E}′.
步骤6 对新证据集{E}′使用D-S规则进行融合,得到空域融合结果.
3.2.2 方案2:丢弃弱相关性证据采用修正最弱相关性证据的空域融合方案在一定程度上提高了后续空域融合的收敛速率,并保证了D-S融合规则的有效性.然而,最弱相关性证据不能充分表征所有干扰和故障证据,进而导致出现这种情况时D-S融合规则的有效性难以保障.基于此,提出从环形证据序列中丢弃表征多个故障和干扰的弱相关性证据的融合方案,进而从根本上消除多个故障或干扰证据对空域融合的影响,并进一步加快融合收敛速率,保证D-S融合的有效性.具体步骤如下.
步骤1 设定一个尽量小的弱相关性判别阈值ηEIR.
步骤2 根据ηEIR找出环形证据序列中所有的弱相关性证据Ei,并将其丢弃,得到一个不完整的证据集{EResidual}.
步骤3 对不完整的证据集{EResidual}使用D-S规则进行融合,得到空域融合结果.
3.2.3 方案3:修正传感器间的证据误差虽然方案2能保证D-S融合规则的有效性,但没有合理表征和处理不同类型传感器间的证据误差,这使得该证据误差仍会影响D-S融合的收敛速度.基于此,提出修正表征传感器间证据误差的一般相关性证据,同时保留强相关性证据并丢弃弱相关性证据的融合方案,以期实现对存在各种相关性差异的证据进行表征和处理,力求保证D-S融合的有效性和收敛速度的同时,使融合结果更符合客观实际.具体步骤如下:
步骤1 设定一个强相关阈值和一个弱相关阈值分别为ηER和ηEIR,用于表征2条证据是强相关或弱相关.
步骤2 根据ηEIR找出所有的弱相关性证据并丢弃,根据ηER找出所有的强相关性证据并保留,将非强相关和弱相关外的其他证据都标记为一般相关性证据,最终得到一个不完整的证据集{EResidual}.
步骤3 计算出不完整的证据集{EResidual}中所有证据在证据集中所占有的权值ωi.
步骤4 计算出不完整的证据集{EResidual}的期望EResidual,计算方法与方案1一致.
步骤5 把不完整的证据集{EResidual}中所有标记为一般相关性证据用证据集期望EResidual进行替换,得到新的不完整的证据集{EResidual}′.
步骤6 对新的不完整的证据集{EResidual}′使用D-S规则进行融合,得到空域融合结果.
4 仿真实例由于所提方法主要用于入侵检测,所以为了验证时空域融合模型的有效性,首先介绍信息融合算法性能的评估标准;然后分3个阶段对模拟智能家居入侵检测系统的红外、声音、振动、微波传感器采集的证据的融合结果性能进行分析;最后对实际入侵进行模拟,进一步说明所提算法的有效性.
4.1 入侵检测系统融合性能体系的研究衡量入侵检测系统的指标体系如图 2所示.由于主要研究时空域信息融合入侵检测算法的能力和性质,所以主要从收敛速度和抗干扰能力2个方面来讨论系统的性能.

|
图 2 入侵检测系统性能评估指标体系 |
1) 收敛速度
对于入侵检测算法而言,理想情况下,当入侵事件发生时,信息融合所得到的检测结果应该与实际入侵发生时的值一致.但是实际上,由于不同传感器所能表征的事件可信度以及融合算法对时间证据处理的方式都不一样的因素,使得当前时刻融合所得到的结果与实际值之间在时间上存在一定的差距,而在后续有利证据不断出现的情况下,融合算法会不断地向实际值逼近,那么逼近实际值的速度,也就是融合结果到达峰值的速度即为收敛速度.收敛速度快,则系统的实时性强;反之,收敛的速度慢,则系统的实时性弱.
2) 抗干扰能力
家庭环境中时常会产生各种干扰观测环境参数的因素,如果对这些干扰因素不进行处理,它们就会对融合算法的结果产生影响,以至于不能得到与实际值近似的融合结果,从而干扰入侵检测系统的正常决策.衡量抗干扰能力主要从融合算法的全局收敛性和局部收敛性2个方面来考虑.全局收敛性表征的是在入侵检测系统整个运行过程中融合得到的结果与实际值之间的均方误差,而局部收敛性则表征的是在某个命题事件发生的时间周期内,融合得到的结果与实际值之间的均方误差.因此,均方误差越小,算法的收敛性越好,抗干扰能力就越强,反之亦然.
4.2 传感器的基本可信度分配设入侵检测的识别框架Θ={人、宠物、没人或没宠物}.各传感器的基本可信度分配如表 1所示.
|
|
表 1 基本可信度映射表 |
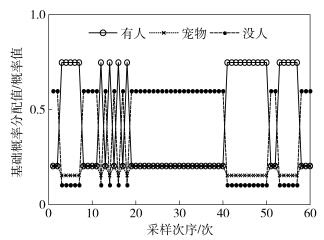
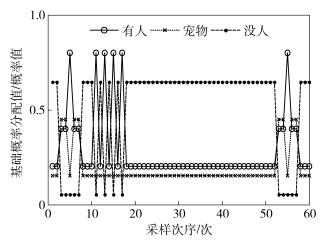
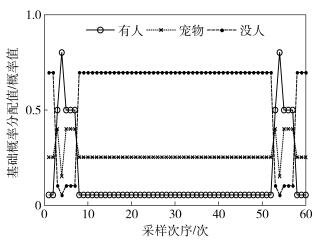
4类传感器采集到的证据如图 3~图 6所示,方案1~方案3的融合结果如图 7~图 9所示,文献[9]和文献[12]的融合结果如图 10~图 11所示.仿真实验过程分3个阶段,第1个阶段为模拟入侵者进入阶段,采样次序为1~10;第2个阶段为模拟干扰及故障阶段,采样次序为20~50,其中10~20为红外传感器和声音传感器受到不同时间间隔上的干扰,30~40为微波传感器受到不同程度的干扰,40~50为红外传感器完全故障检测结果数值一直持续处于最大值;第3个阶段为再次模拟入侵者进入阶段,采样次序为50~60.为叙述方便,采样次序用t表示.
|
图 3 红外传感器证据 |
|
图 4 声音传感器证据 |
|
图 5 振动传感器证据 |

|
图 6 微波传感器证据 |
|
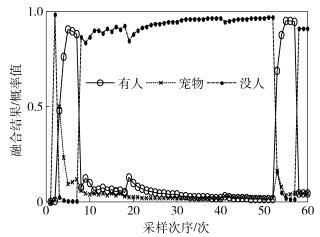
图 7 方案1融合结果 |
|
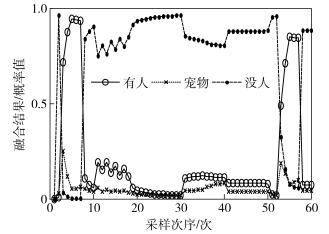
图 8 方案2融合结果 |
阶段1 比较图 7~图 11,文献[9]、文献[12]、方案3的收敛性比较好,而方案2、方案1略差,它们最终都能得到“有人”的收敛结果;从收敛速度上看,方案3最快在t=3的时候就已经收敛,方案1和方案2则是在t=4时才收敛,而文献[9]和文献[12]则需t=5时的证据才趋近于完全收敛,需要采集的证据更多,影响融合的时效性.由此可见,提出的方案3具有更快的收敛速度,融合结果能够更快地收敛于真实环境,具有很强的实时性.
阶段2 通过表 2计算了各个方案及文献在干扰模拟阶段的均方误差,可以看出文献[9]方法的抗干扰性最弱,究其原因是采用单纯的D-S算法融合时忽略了时空域的证据特点,因此会造成D-S融合算法“一票否决”的缺陷.方案1的均方误差最小,在第2个阶段的局部收敛性也是最好,抗干扰能力最强,其次是方案3,再次是方案2、文献[12].由此看以看出,在模拟入侵检测受到干扰方面,采用修正证据集的方式能够有效地识别干扰,并且起到了排除干扰的作用.
阶段3 比较图 7~图 11,方案1~方案3及文献[12]的方法均能检测到入侵者的再次进入,而文献[9]方法在阶段2融合收敛于“没人”的结果后就一直保持不变,以致于入侵者在阶段3再次进入时未能检测到.究其根本原因还是D-S算法的“一票否决”缺陷,当证据间的冲突太大时,融合规则已完全失效.对于文献[12],相同的证据在第1个阶段和第3个阶段融合的效果不同,收敛性也明显降低,进而说明文献[12]采用人为设定权值的情况下进行证据融合,无法合理地表征出历史证据与实时证据之间的联系,因此影响了融合结果.而于此同时,方案1~方案3则表现出了融合算法优良的鲁棒性,在经过干扰后,依然能够很好地收敛并识别出入侵.
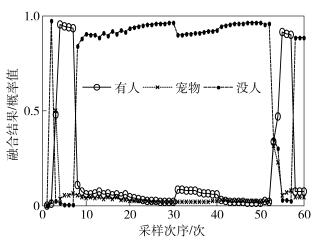
|
图 9 方案3融合结果 |
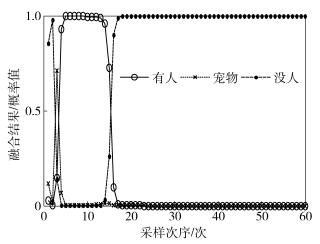
|
图 10 文献[9]融合结果 |
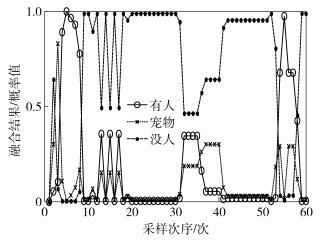
|
图 11 文献[12]融合结果 |
|
|
表 2 第2个阶段各方案的均方误差 |
通过分析仿真实例3个阶段的性能,可以看出所提出的时空域信息融合模型及相应的入侵检测算法能有效降低空域融合证据间的冲突,提高融合算法的收敛速度,增强融合算法的抗干扰能力,并加强决策系统的鲁棒性和实时性.
4.4 入侵行为模拟及分析为了对智能家居入侵检测系统的信息融合能力进行全面的测试和评估,参照信息融合性能测试基准,通过如下方式模拟入侵行为,进一步验证所提算法的性能.
家中部署的传感器节点如图 12所示,传感器每0.5 s采集一次环境参数信息,其中编号相同的各类传感器在空域进行融合.现有一个非法入侵者要进行入家中盗窃,其行动轨迹如图 12中的箭头所示.非法入侵者在t=2时以暴力手段打开大门进入家中,在破门而入时引起了门的振动并发出了声音;然后以步行方式静悄悄地进入室内,在t=52时打开主卧室门并进入行窃.在模拟这一过程中,第1组传感器与第2组传感器参照5个方案得到的“有人”事件的融合结果如图 13所示,相应衡量各方案抗干扰能力的局部均方误差如表 3所示.
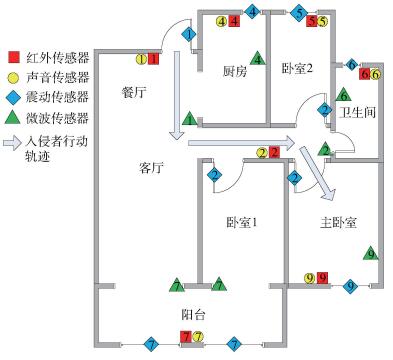
|
图 12 家中传感器节点部署方案 |
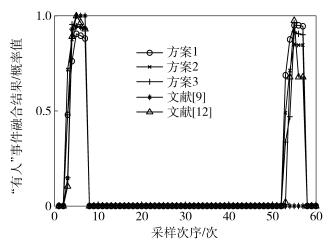
|
图 13 模拟入侵检测结果 |
|
|
表 3 模拟入侵的均方误差 |
由图 13可以看出,所提方案在入侵检测上具有一定的优势,在t=3时方案3就已经收敛于融合算法峰值,能够在入侵事件发生时快速识别入侵事件.此外,既便非法入侵者进入卧室时刻意规避声音传感器采集的信息或者缓慢移动以规避微波传感器的检测,提出的入侵检测系统依然能够检测到入侵事件.由表 3模拟入侵检测抗干扰能力的局部均方误差对比结果可以看出,所提方案与现有算法相比具有更好的收敛性,进一步证明了所提方案具有更好的抗干扰和规避故障的能力,从而能提升检测的准确性.
5 结束语笔者通过分析时域和空域证据融合的特点,提出了一种新的时空域信息融合入侵检测模型及方法.该方法能提高信息融合的收敛速度和抗干扰能力,并增强智能家居入侵检测系统的实时性和鲁棒性,同时还能提高入侵检测的准确率,保证融合结果在高度冲突情况下依然能够决策出符合客观实际的结果.仿真实例验证了所提方法的可行性,另外也为证据理论在时空域的研究提供了一种新的思路.
| [1] | Jousselme A L, Grenier D, Bosse E. A new distance between two bodies of evidence[J]. Information Fusion, 2001, 2(2): 91–101. doi: 10.1016/S1566-2535(01)00026-4 |
| [2] | Smets P. Decision making in the TBM:the necessity of the pignistic transformation[J]. International Journal of Approximate Reasoning, 2005, 38(2): 133–147. doi: 10.1016/j.ijar.2004.05.003 |
| [3] | Liu Weiru. Analyzing the degree of conflict among belief function[J]. Artificial Intelligence, 2006, 170(11): 909–924. doi: 10.1016/j.artint.2006.05.002 |
| [4] |
肖建于, 童敏明, 朱昌杰, 等. 基于pignistic概率距离的改进证据组合规则[J]. 上海交通大学学报, 2012, 46(4): 636–641, 645.
Xiao Jianyu, Tong Minming, Zhu Changjie, et al. Improved combination rule of evidence based on pignistic probability distance[J]. Journal of Shanghai Jiao Tong University, 2012, 46(4): 636–641, 645. |
| [5] |
熊彦铭, 杨战平, 屈新芬. 基于模型修正的冲突证据组合新方法[J]. 控制与决策, 2011, 26(6): 883–887.
Xiong Yanming, Yang Zhanping, Qu Xinfen. Novel combination method of conflict evidence based on evidential model modification[J]. Control and Decision, 2011, 26(6): 883–887. |
| [6] |
郭华伟, 施文康, 刘清坤, 等. 一种新的证据组合规则[J]. 上海交通大学学报, 2006, 40(11): 1895–1900.
Guo Huawei, Shi Wenkang, Liu Qingkun, et al. A new combination rule of evidence[J]. Journal of Shanghai Jiao Tong University, 2006, 40(11): 1895–1900. doi: 10.3321/j.issn:1006-2467.2006.11.018 |
| [7] |
赵秋月, 左万利, 田中生, 等. 一种基于改进D-S证据理论的信任关系强度评估方法研究[J]. 计算机学报, 2014, 37(4): 873–883.
Zhao Qiuyue, Zuo Wanli, Tian Zhongsheng, et al. A method for assessment of trust relationship strength based on the improved D-S evidence theory[J]. Chinese Journal of Computers, 2014, 37(4): 873–883. |
| [8] |
毕文豪, 张安, 李冲. 基于新的证据冲突衡量的加权证据融合方法[J]. 控制与决策, 2016, 31(1): 73–78.
Bi Wenhao, Zhang An, Li Chong. Weighted evidence combination method based on new evidence conflict measurement approach[J]. Control and Decision, 2016, 31(1): 73–78. |
| [9] | Hong Lang, Lynch A. Recursive temporal-spatial information fusion with applications to target identification[J]. IEEE Transactions on Aerospace & Electronic Systems, 1993, 29(2): 435–445. |
| [10] | Yun Lin, Gao Lipeng, Li Yibing, et al. The application of improving space-time DS evidence theory in distinguishing vehicle[C]//Asia Pacific Conference on Postgraduate Research in Microelectronics & Electronics.[S.l.]:IEEE, 2009:376-379. |
| [11] |
罗大庸, 张远. 多传感器信息时空融合模型及算法研究[J]. 系统工程与电子技术, 2004, 26(1): 36–39.
Luo Dayong, Zhang Yuan. Research of spatial-temporal architecture model and the algorithm for multisensory information fusion[J]. Systems Engineering and Electronics, 2004, 26(1): 36–39. |
| [12] | Weeraddana D M, Kulasekere C, Walgama K S. Dempster-Shafer information filtering framework:temporal and spatio-temporal evidence filtering[J]. IEEE Sensors Journal, 2015, 15(10): 5576–5583. doi: 10.1109/JSEN.2015.2442153 |
| [13] | Weeraddana D, Walgama K S, Kulasekere e C. Dempster-Shafer information filtering in multi-modality wireless sensor networks[C]//World Academy of Science, Engineering and Technology, 2013:871-877. |
| [14] | Shafer G. A Mathematical Theory of Evidence[M]. Princeton: Princeton University Press, 1976. |
| [15] | Dempster A P. Upper and lower probabilities-induced by a multivaluedmapping[J]. Annals of Mathematical Statistics, 1967, 38(2): 325–339. doi: 10.1214/aoms/1177698950 |


