为了解决当前车载网隐私保护机制的安全性和效率问题,基于安全多方计算理论和匿名认证协议,提出了一种新的车载网节点隐私保护方案.该方案利用线性方程组的求解理论,采用安全高效的茫然传输机制,避开了传统的计算复杂的公钥密码算法.对方案的安全性和效率分析的结果表明,新方案不仅能够解决车载网中发送者隐私、接收者隐私、匿名性、共谋攻击、重放攻击等多种安全问题,而且认证效率也得到了有效提高,在计算性能受限的物联网环境中,具有理论和应用价值.
To solve the security and efficiency problem of the existing privacy protection schemes in vehicular network, a new privacy protection scheme was proposed based on security multi-party computation and anonymous authentication. Because of linear equations and secure and efficient oblivious transfer mechanism, the traditional public key cryptography algorithm is avoided. It is shown that the proposed scheme not only can fulfill multiple security requirements, such as privacy of sender, privacy of receiver, anonymity, collusion attack, replay attack, etc, but also can improve the authentication efficiency. The scheme is of significance and application value in limited computational performance environments such as Internet of Things.
匿名认证是解决车载网隐私问题的重要方法之一. Raya等[1]首次提出了一种基于别名证书的车载网匿名认证协议. Lu等[2]设计了一种基于身份ID的车载网认证框架. Zeng等[3]提出了一种基于环签名的匿名认证方案,消息认证所需时间随证书更新列表呈线性增长. Lin等[4]提出了一种基于群签名的车载自组织网络(VANET, vehicular ad hoc network)认证方案,以降低密钥存储空间与证书更新列表传输消耗.文献[5-6]的方案能够实现新成员的加入.文献[7-10]的方案能够实现成员的更新(加入和撤销).但在文献[6]和文献[10]方案中,一个群成员退出会影响该组其他群成员的密钥,造成全局的变化,不能满足VANET的高动态需求.目前这些方案均采用传统的公钥密码机制设计而成,算法复杂,效率较低.然而,安全多方计算[11]在解决隐私问题方面具有明显的优势,并已经存在一些相关具体应用[12].笔者针对现存传统车载网隐私保护方法的不足,结合安全多方计算的优势,基于线性方程组的求解理论,设计了一种新的车载网隐私保护方案,有效地解决了车载网匿名认证过程中的计算瓶颈问题.
1 预备知识 1.1 符号说明本方案用到的相关符号含义如表 1所示.
|
|
表 1 符号说明 |
定理1 n元线性方程组Ax=b有解的充分必要条件是系数矩阵A的秩等于增广矩阵A的秩,即R(A)=R(A).
定理2 若n元线性方程组Ax=b有解,如果R(A)=n,那么方程组只有唯一解;如果R(A)<n,那么方程组有无穷多解.
1.3 安全性假设茫然传输协议的安全性基于决策性Diffie-Hellman(DDH, decisional Diffie-Hellman)假设. DDH假设:g为阶为素数q的群G的生成元,p=2q+1.任意g∈Gq/{1}及a, b, c属于有限域Zq,则Y1=(g, ga, gb, gab)和Y2=(g, ga, gb, gc) 2个分布是计算不可区分的.
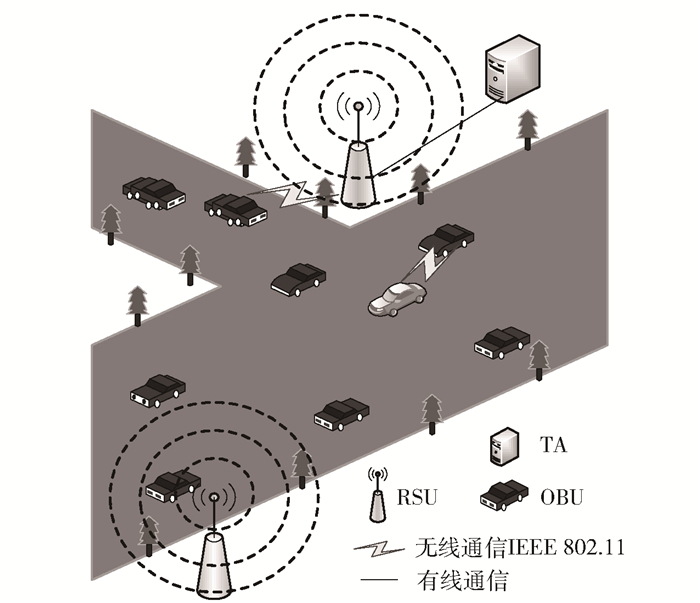
1.4 VANET结构与传统的互联网不同,VANET主要采用无线的通信方式,通信实体为车辆.系统模型包括3个部分:可信服务中心(TA, trust authority)、路侧单元(RSU, road side unit)和车辆单元(OBU, on board unit).通信主要由OBU与RSU之间的通信和车辆与车辆之间的通信2部分组成.系统网络模型如图 1所示.
|
图 1 典型VANET网络模型 |
1) TA
TA主要负责存储所有经过认证的车辆用户的隐私信息,为系统生成公私钥对和系统参数.
2) RSU
RSU是安装在道路两侧的基础设施,能够通过无线与车辆通信,类似无线传感网络的接入节点.
3) OBU
在VANET中每个车辆都配备了无线通信模块OBU,通过OBU使得车辆能够与RSU或者其他配备OBU的车辆进行通信.
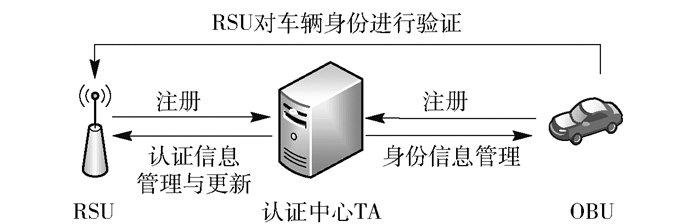
2 本文方案笔者提出的基于安全多方计算的车载网隐私保护方案包含3个阶段:注册阶段、认证阶段和更新阶段.总体认证框架如图 2所示.注册阶段:车辆节点Vp和RSU节点Rs在TA处进行注册登记,TA为它们颁发各自的认证信息.认证阶段:若Vp进入某个区域并需同Rs进行通信,Rs首先对Vp进行匿名认证.更新阶段:当有车辆节点加入或撤离后,Vp与Rs定期到TA更新认证信息.
|
图 2 车辆节点OBU与RSU的认证框架 |
方案具体过程如下:
1) 注册阶段
步骤1 TA随机生成一个m×n维的矩阵A(2≤m<n)和一个m维的列向量y,满足R(A)=R(A),且R(A)<n,即线性方程组Ax=y有无穷多解.
步骤2 TA为每个合法车辆节点生成唯一的n维向量xi,且xi满足Axi=y,即xi为线性方程组Ax=y的一个解. TA将向量xi颁发给相应的车辆节点Vp作为其身份信息,相应地,TA将矩阵A和向量y通过安全信道发送给每个Rs节点作为认证信息.
2) 认证阶段
当Vp进入Rs区域需要进行通信时,Vp向Rs发送身份认证请求,Rs对其身份进行认证,判定其是否为合法用户.
步骤1 Vp向Rs发送认证请求,并且Vp随机选择2个G的生成元g、h,并发送(g, h)给Rs.
步骤2 Rs收到车辆节点的认证请求之后,随机选择k∈Zq,产生k个随机矩阵D1, D2, …, Dk,使A=D1+D2+…+Dk. Rs产生一个秘密随机数t,令t>k,Rs发送(H1, H2, …, Ht)给Vp,其中Hi=Dj(这里i与j都是随机的),在(H1, H2, …, Ht)中,除Hi外,其余的均为随机矩阵.
步骤3 对所有的i=1, 2, …, t,Vp计算Hix+rj,这里rj是一个随机向量. Vp拥有t个消息m1, m2, …, mt,其中m1=H1x+r1, m2=H2x+r2, …, mt=Htx+rt. (δ1, δ2, …, δk)⊂(1, 2, …, t)表示Rs选择的k个消息mδ1, mδ2, …, mδk.利用茫然传输协议,Rs取回结果Hix+rj=Djx+rj.
① Rs计算f′(x)=(x-δ1)(x-δ2)…(x-δk)=b0+b1x+…+xk. Rs再随机选择一个多项式f(x)=a0+a1x+…+ak-1xk-1+xk,随机选取ai∈Zq(0≤i≤k),并计算A0=ga0hb0modp, A1=ga1hb1modp, …, Ak-1=gak-1hbk-1 modp发送给Vp.
② Vp随机选择l∈Zq并计算:
| $ \begin{array}{*{20}{l}} {{B_i}{\rm{ = }}{g^{lf(i)}}{h^{lf'(i)}}{\rm{ = }}{{({A_{\rm{0}}}A_1^i\mathit{A}_2^{{i^{\rm{2}}}}A_{k{\rm{ - 1}}}^{{i^{k{\rm{ - 1}}}}}{{\left( {gh} \right)}^{{i^k}}})}^l}{\rm{mod}}\;p}\\ {\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{C}}_i}{\rm{ = }}{\mathit{\boldsymbol{m}}_i}{B_i}{\rm{mod}}p}\\ {\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{r}}{\rm{ = }}\sum\limits_{j{\rm{ = 1}}}^k {{\mathit{\boldsymbol{r}}_j}} } \end{array} $ |
其中i=1, 2, …, t,然后发送(r, gl, C1, …, Ct)给Rs.
③ 对于i=δ1,δ2,…,δk,Rs计算m′δi=Cδi((gl)f(δi))-1,这里((gl)f(δi))-1(gl)f(δi)=1modp,则(m′δ1, m′δ2, …, m′δk)正是Rs所选择的k个消息Hix+rj=Djx+rj,其中i=1, 2, …, k.
步骤4 Rs计算:
| $ \begin{array}{l} \mathit{\boldsymbol{W}}{\rm{ = }}\sum\limits_{\mathit{j}{\rm{ = 1}}}^\mathit{t} {{\mathit{\boldsymbol{D}}_\mathit{j}}\mathit{x}} {\rm{ + }}\sum\limits_{\mathit{j}{\rm{ = 1}}}^\mathit{t} {{\mathit{\boldsymbol{r}}_\mathit{j}}} {\rm{ = }}\mathit{\boldsymbol{Ax}}{\rm{ + }}\mathit{\boldsymbol{r}}\\ \;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{y' = W - r}}{\rm{ = }}\mathit{\boldsymbol{Ax}}{\rm{}} \end{array} $ |
若y′=y则认证通过,否则拒绝该认证消息.
3) 更新阶段
由方程组
| $ \left. \begin{array}{l} \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}_{\rm{1}}}{\rm{ = }}\mathit{\boldsymbol{y}}\\ \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}_{\rm{2}}}{\rm{ = }}\mathit{\boldsymbol{y}}\\ \;\;\;{\rm{ \ldots }}\\ \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}_\mathit{n}}{\rm{ = }}\mathit{\boldsymbol{y}} \end{array} \right\} $ |
当x1, x2, …, xn已知时,可求A和y.其中,A是m×n阶矩阵,y是m维列向量.在VANET中,若有新节点加入或者节点撤销,可以利用现有的节点x,由注册服务器重新计算A和y的一个解,并作为认证信息发送给Rs.
3 方案分析 3.1 安全性分析1) 发送者的隐私
首先发送者的隐私是计算安全的.
在DDH假设的基础上,接收者都是半诚实的,则接收者接收到其他t-k个消息的概率是可以忽略的.
证明:如果接收者能通过算法β以不可忽略的概率ε接收到其他t-k个消息,则接收者能以不可忽略的概率区分作为DDH问题的2个分布Y1与Y2.
β的输入为(g, u, v, w)(可能属于Y1也可能属于Y2),β计算(g1, g2, h1, h2, Gq, p),其中g1=g,g2=u,h1=v,h2=w,然后β与接收者执行茫然传输协议.
① R选择2个多项式:
| $ \begin{array}{l} \mathit{f'}\left( \mathit{x} \right){\rm{ = (}}\mathit{x - }{\mathit{\delta }_{\rm{1}}}{\rm{)(}}\mathit{x - }{\mathit{\delta }_{\rm{2}}}{\rm{) \ldots (}}\mathit{x - }{\mathit{\delta }_\mathit{k}}{\rm{)mod}}\mathit{p}{\rm{ = }}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{b}_{\rm{0}}}{\rm{ + }}{\mathit{b}_{\rm{1}}}\mathit{x}{\rm{ + \ldots + }}{\mathit{x}^\mathit{k}}\\ \mathit{f}\left( \mathit{x} \right){\rm{ = }}{\mathit{a}_{\rm{0}}}{\rm{ + }}{\mathit{a}_{\rm{1}}}\mathit{x}{\rm{ + \ldots + }}{\mathit{a}_{\mathit{k}{\rm{ - 1}}}}{\mathit{x}^{\mathit{k}{\rm{ - 1}}}}{\rm{ + }}{\mathit{x}^\mathit{k}}{\rm{, }}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{a}_\mathit{i}} \in {\mathit{Z}_\mathit{q}}\left( {{\rm{0}} \le \mathit{i} \le \mathit{k}} \right){\rm{}} \end{array} $ |
② R→β:
| $ {\mathit{A}_{\rm{0}}}{\rm{ = }}\mathit{g}_2^{{\mathit{a}_{\rm{0}}}}\mathit{h}_2^{{\mathit{b}_{\rm{0}}}}{\rm{mod}}\mathit{p}{\rm{, \ldots, }}{\mathit{A}_{\mathit{k - }{\rm{1}}}}{\rm{ = }}\mathit{g}_2^{{\mathit{a}_{\mathit{k} - 1}}}\mathit{h}_2^{{\mathit{b}_{\mathit{k} - 1}}}{\rm{mod}}\mathit{p} $ |
③ β随机选择l∈Zq,对于i=1, 2, …, t,计算:
| $ \begin{array}{*{20}{l}} {{B_i}{\rm{ = }}g_2^{lf(i)}h_2^{lf'(i)}{\rm{ = }}{{({A_{\rm{0}}}A_1^i{\rm{A}}_2^{{i^{\rm{2}}}}A_{k{\rm{ - 1}}}^{{i^{k{\rm{ - 1}}}}}{{\left( {{g_{\rm{2}}}{h_{\rm{2}}}} \right)}^{{i^k}}})}^l}{\rm{mod}}p}\\ {\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{C}}_i}{\rm{ = }}{\mathit{\boldsymbol{m}}_i}{B_i}{\rm{mod}}p} \end{array} $ |
④ β→R:
g2l=g1al(al是有限域Zq中的随机数),C1, C2, …, Ct.
⑤ R→β:任何的k+1个消息{mβ1, …, mβk+1}⊆{m1, …, mt},如果这k+1个消息都正确,β输出1,否则输出0.很明显,如果R仅通过猜测去取得其他消息,β输出1的概率是1/q.
如果(g, u, v, w)来自Y1,则Bi=g2lf(i)h2lf′(i)=ulf(i)wlf′(i)=galf(i)gablf′(i)=(g1f(i)h1f′(i))al是一个有效的加密形式;如果(g, u, v, w)来自Y2,Bi=g2lf(i) h2lf′(i)=ulf(i)wlf′(i)=galf(i)ga′blf′(i)≠(g1f(i)h1f′(i))al不是一个有效的加密形式.因为r是随机选择的,Bi在Gq上呈均匀分布,所以接收者接收到其他消息的概率是1/q.很明显,接收者仍能接收到他所选择的k个消息.
如果β输出1的概率大于ε+1/q,则β能够计算出(g, u, v, w)是来自于分布Y1;如果β输出1的概率小于ε+1/q,则β能够计算出(g, u, v, w)是来自于分布Y2.这样,β能以不可忽略的概率区分DDH.所以,发送者的隐私在计算上是安全的.
2) 接收者的隐私
对于任意不同的(δ′1, δ′2, …, δ′k),都会确定一个k阶多项式f′1(x)=(x-δ′1)(x-δ′2)…(x-δ′k)=b′0+b′1x+…+xk,且存在一个k阶多项式f1(x)=a′0+a′1x+…+a′k-1xk-1+xk满足Ai=ga′ihb′i(0≤i≤k-1),所以根据接收者发出的消息Ai并不能获得接收者所选择的消息信息,即接收者的隐私是无条件安全的.根据此应用环境的具体问题,考虑到碰撞攻击,Vp猜对接收者消息的概率是1/Ctk,此概率和k和t相关.假设当发送者Vp成功实现碰撞攻击时,根据
3) 匿名性
本方案通过茫然传输协议实现车辆的匿名性.当Vp和Rs执行茫然传输协议时,Vp计算参数(r, gl, C1, …, Ct)并将其发送给Rs.然后,Rs计算y′ W-r,并判断y′
4) 共谋攻击
假定有n个车辆节点串谋,企图计算出Rs节点的秘密认证向量A和y,它们将各自的认证信息进行组合,建立方程组:
| $ \left. \begin{array}{l} \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}_{\rm{1}}}{\rm{ = }}\mathit{\boldsymbol{y}}\\ \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}_{\rm{2}}}{\rm{ = }}\mathit{\boldsymbol{y}}\\ \;\;\;{\rm{ \ldots }}\\ \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}_\mathit{n}}{\rm{ = }}\mathit{\boldsymbol{y}} \end{array} \right\} $ |
其中:A是未知的m×n阶矩阵,y是未知的m维列向量.显然,在上述方程组中,共有m×n+m个未知数,而只有m×n个等式.利用m×n个等式求解m×n+m个未知数,有无穷解,即矩阵A和向量y不唯一.所以,尽管n个共谋者可以建立方程组试图求解A和y,但由于解有无穷多个,不能以不可忽略的概率选出Rs的秘密认证向量A和y.
5) 重放攻击
假设某个恶意车辆节点截获了Vp发送给Rs的信息,并企图伪装成Vp向Rs申请认证.由于在每次Rs对Vp认证过程中,Rs均会生成新的(H1, H2, …, Ht),其中t-k个矩阵是随机的,t为秘密随机数,Hix+rj中的rj是Vp在生成验证信息时生成的随机向量.因此,若恶意车辆发送给Rs旧的验证过的消息Hix+rj请求认证,以不可忽略的概率通过验证请求是不可能的.
本方案与现有典型方案的安全性能对比如表 2所示.
|
|
表 2 安全性比较 |
为了便于跟文献[3]、文献[4]和文献[7]方案的计算开销进行比较,分别用Tmul表示执行一次乘法所需要的时间,Texp表示执行一次幂指数运算所需要的时间,Tin表示执行一次求逆运算所需要的时间,Tpar表示执行一次双线性映射操作所需要的时间,Th表示执行一次Hash操作所需要的时间.文献[3]方案中n表示组成员的个数,Ncrl表示证书更新列表的数目.本方案中:
Vp的计算开销为3mTmul+2mTexp;
Rs的计算开销为4kTmul+(4k-2)Texp+kTin.
算法复杂性比较结果如表 3所示.
|
|
表 3 算法复杂性比较 |
通过表 3可明显看出,其他典型方案均存在公钥密码体制中的双线性映射操作运算,而一次双线性对的运算所需时间远远大于表中其他类型的一次操作运算所需时间.尽管本方案中存在参数k和t(k表示在认证阶段步骤2中Rs生成的随机矩阵Di(i∈{1, 2, …, k})的个数,t表示步骤3中Vp拥有的消息个数),但是总计算开销相对于基于公钥密码的方案依然有较大的优势.此外,在通信过程中信息交互的次数方面,RSU节点与车辆节点之间仅需要交互4次.因此,本方案在效率方面有明显提高.
4 结束语针对现有车载网隐私保护方案的安全和效率问题,提出了一种基于安全多方计算的车载网隐私保护方案.该方案通过结合线性方程组理论、匿名认证思想与茫然传输协议,成功解决了车载网中的发送者隐私、接收者隐私、匿名性、共谋攻击和重放攻击等安全问题,并彻底避开了传统的计算复杂的公钥密码算法.因此,本方案在计算性能受限的车载网环境中,有着重要的理论意义和应用价值.
| [1] | Raya M, Hubaux J P. Securing vehicular ad hoc networks[J]. Journal of Computer Security, 2007, 15(1): 39–68. doi: 10.3233/JCS-2007-15103 |
| [2] | Lu Huang, Li Jie, and M. Guizani. A novel ID-based authentication framework with adaptive privacy preservation for VANETs[J]. Computing, Communications and Applications Conference IEEE, 2012: 345–350. |
| [3] | Zeng Shengke, Huang Yuan, Liu Xingwei. Privacy-preserving communication for VANETs with conditionally anonymous ring signature[J]. International Journal of Network Security, 2015, 17(2): 135–141. |
| [4] | Lin Xiaodong, Sun Xiaoting, Ho P H, et al. Gsis:a secure and privacy-preserving protocol for vehicular communications[J]. IEEE Transactions on Vehicular Technology, 2007, 56(6): 3442–3456. doi: 10.1109/TVT.2007.906878 |
| [5] | Liu Hui, Li Hui, Ma Zhanxin. Efficient and secure authentication protocol for VANET[C]//International Conference on Computational Intelligence and Security.[S.l.]:IEEE Computer Society, 2010:523-527. |
| [6] | Mamun M S I, Miyaji A, Takada H. A multi-purpose group signature for vehicular network security[C]//International Conference on Network-Based Information Systems.[S.l.]:IEEE, 2014:511-516. |
| [7] | Shao Jun, Lin Xiaodong, Lu Rongxing, et al. A Threshold Anonymous Authentication Protocol for VANETs[J]. IEEE Transactions on Vehicular Technology, 2016, 65(3): 1711–1720. doi: 10.1109/TVT.2015.2405853 |
| [8] | Zhu Xiaoyan, Jiang Shunrong, Wang Liangmin, et al. Privacy-preserving authentication based on group signature for VANETs[C]//Globecom Workshops.[S.l.]:IEEE, 2013:4609-4614. |
| [9] | Zhu Xiaoyan, Jiang Shunrong, Wang Liangmin, et al. Efficient privacy-preserving authentication for vehicular ad hoc networks[J]. IEEE Transactions on Vehicular Technology, 2014, 63(2): 907–919. doi: 10.1109/TVT.2013.2294032 |
| [10] | He Li, Zhu Wentao, Mitigating dos attacks against signature-based authentication in VANETs[C]//IEEE International Conference on Computer Science and Automation Engineering.[S.l.]:IEEE, 2012:261-265. |
| [11] |
刘文, 罗守山, 杨义先, 等. 安全两方圆计算协议[J]. 北京邮电大学学报, 2009, 32(3): 32–35.
Liu Wen, Luo Shoushan, Yang Yixian, et al. A study of secure two-party circle computation problem[J]. Journal of Beijing University of Posts and Telecommunications, 2009, 32(3): 32–35. |
| [12] | Sundari S, Ananthi M. Secure multi-party computation in differential private data with Data Integrity Protection[C]//International Conference on Computing and Communications Technologies.[S.l.]:IEEE, 2015:180-184. |
| [13] | Shi Runhua, Zhong Hong, Huang Liusheng. A novel anonymous authentication scheme without cryptography[J]. Transactions on Emerging Telecommunications Technologies, 2014, 25(9): 875–880. doi: 10.1002/ett.v25.9 |


