为了充分利用大规模多输入多输出(MIMO，multiple-input multiple-output)系统的多天线技术，需要配置与天线数目同样多的射频(RF, radio frequency)链路(RF链路包括低噪声放大器、混合器、模数/数模转换器等^[1])，这导致系统的硬件复杂度增加，同时天线单元消耗的能量也增加，成为大规模MIMO技术发展中一个不可忽视的限制因素.对此，天线选择^[2-4]是一个较为有效的技术解决方案，利用大规模MIMO多天线的空间选择性，提高系统分集增益，从而减少系统的硬件复杂度以及能量损耗，且基本不损害系统的性能.

提出一种适应于大规模MIMO系统下行链路的联合天线选择与递减用户调度(JAS-DUS，joint antenna selection and decremental user scheduling)方案.当系统RF链路数有限，通过同时删除对系统性能贡献较小的用户和基站天线，实现在天线选择的同时，调度小区内的最优用户进行通信，以最大化系统总速率，降低计算复杂度.

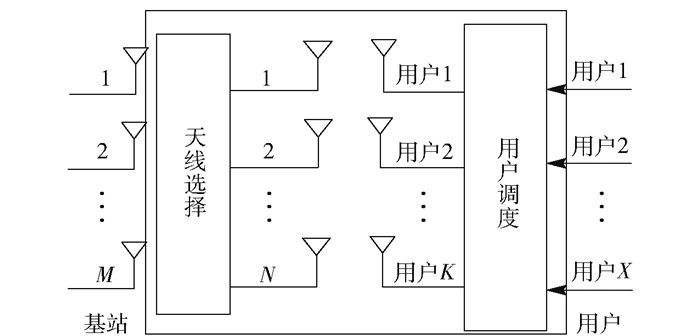
1 系统模型与问题公式化 1.1 系统模型

图 1为一个单小区大规模MIMO系统下行链路联合天线选择与用户调度框图.基站配置发射天线数为M，小区内有大量的单天线用户，总数为X，其中M≥X.从基站选择N个天线，并调度小区内K个用户，满足N≥K，进行同时通信，对应的集合分别定义为选择天线集A、调度用户集U.令H=[h₁^H, h₂^H, …, h_X^H]^H∈$ \mathbb{C}$^X×M表示全部信道状态矩阵，其中h_i=[h_i1, h_i2, …, h_iM]∈$ \mathbb{C}$^1×M.设联合天线选择与用户调度迭代过程中，天线集与用户集分别为A_t、U_t，|·|表示集合的势，则对应天线数与用户数分别为|A_t|、|U_t|，信道矩阵H=[h₁^H, h₂^H, …, h_|Ut|^H]^H∈ $ \mathbb{C}$^|U_t|×|A_t|，其中h_i=[h_i1, h_i2, …, h_i|At|]∈ $ \mathbb{C}$^1×|A_t|.假设信道传输环境为平坦衰落，系统工作在时分双工(TDD，time division duplexing)模式，基站可以获得全部的信道状态信息.

基站端发射信号x∈$ \mathbb{C}$^|A_t|×1为传输信号数据流s∈$ \mathbb{C}$^|U_t|×1与波束成形矩阵W=[w₁, w₂, …w_|Ut|]∈$ \mathbb{C}$^|A_t|×|U_t|的结合，即

$ \mathit{\boldsymbol{x = W}}{\mathit{\boldsymbol{P}}^{\frac{1}{2}}}\mathit{\boldsymbol{s = }}\sum\limits_{i = 1}^{\left| {{U_{\text{t}}}} \right|} {{\mathit{\boldsymbol{w}}_i}\sqrt {{p_i}} {s_i}} $

(1)

其中：p_i为功率分配因子，P=diag(p₁, p₂…, p_|Ut|).经过信道后接收到的信号为

$ \mathit{\boldsymbol{y = \bar Hx + n = \bar HW}}{\mathit{\boldsymbol{P}}^{\frac{1}{2}}}\mathit{\boldsymbol{s + n}} $

(2)

其中：n=[n₁, n₂, …, n_|Ut|]^H∈$ \mathbb{C}$^|U_t|×1是用户信道中的噪声，服从均值为0，方差为1的高斯分布.第i个选择用户所接收到的信号为

$ {y_i} = {{\mathit{\boldsymbol{\bar h}}}_i}{\mathit{\boldsymbol{w}}_i}\sqrt {{p_i}} {s_i} + \sum\limits_{l \ne i,l \in {{U_{\text{t}}}}} {{{\mathit{\boldsymbol{\bar h}}}_i}{\mathit{\boldsymbol{w}}_l}\sqrt {{p_l}} {s_l} + {n_i}} $

(3)

在这里公式右边第1项为用户i的目标信号，第2项为其他用户对用户i的干扰，最后一项表示噪声.其中w_i∈$ \mathbb{C}$^|A_t|×1表示波束成形矩阵的第i列，s_i表示发射到用户i的信号数据流.

假设采用迫零(ZF, zero forcing)波束成形，式(3) 的第2项用户干扰项为0，用户i∈U_t的接收信噪比(SNR，signal to noise ratio)为

$ {r_i}\left( {{A_{\rm{t}}},{U_{\rm{t}}}} \right) = {p_i}{\left| {{{\mathit{\boldsymbol{\bar h}}}_i}{\mathit{\boldsymbol{w}}_i}} \right|^2} $

(4)

满足

$ \sum\limits_{i \in {U_{\rm{t}}}} {\lambda _i^{ - 1}{p_i} \le P} $

其中：$ {\mathit{\lambda }_\mathit{i}}\frac{1}{{{{\left\| {{\mathit{\boldsymbol{w}}_\mathit{i}}} \right\|}^2}}}$表示用户i的有效信道增益^[5]，P为总传输功率.

所以系统总传输速率可以表示为

$ R\left( {{A_{\rm{t}}},{U_{\rm{t}}}} \right) = \sum\limits_{i \in {U_{\rm{t}}}} {\left( {1 + {r_i}\left( {{A_{\rm{t}}},{U_{\rm{t}}}} \right)} \right)} $

(6)

1.2 问题公式化

将联合天线选择与用户调度最优化问题进行公式化：

$ \mathop {\max }\limits_{{A_{\rm{t}}},{U_{\rm{t}}}} R\left( {{A_{\rm{t}}},{U_{\rm{t}}}} \right) = \mathop {\max }\limits_{{A_{\rm{t}}},{U_{\rm{t}}}} \sum\limits_{i \in {U_t}} {{\rm{lb}}\left( {1 + {r_i}\left( {{A_{\rm{t}}},{U_{\rm{t}}}} \right)} \right)} $

(7)

约束于

$ \left| {{\mathit{U}_{\rm{t}}}} \right| \le \left| {{A_{\rm{t}}}} \right| \le N $

(8)

$ \sum\limits_{m \in {A_{\rm{t}}}} {\sum\limits_{i \in {U_{\rm{t}}}} {\lambda _i^{ - 1}{p_i} \le P} } $

(9)

这里约束条件(8) 是确保选择天线数不超过限定RF链路数量，且调度的用户数不超过基站选择的天线数.约束条件(9) 则是功率约束条件.这里选用注水法求最优功率分配，满足

$ {p_i} = {\left( {\mu \lambda _i^{ - 1} - \frac{1}{{{{\left| {{{\mathit{\boldsymbol{\bar h}}}_i}{\mathit{\boldsymbol{w}}_i}} \right|}^2}}}} \right)^ + } $

(10)

其中(x)⁺=max{x, 0}. μ是注水法水位，满足下列条件：

$ \sum\limits_{m \in {A_{\rm{t}}}} {\sum\limits_{i \in {U_{\rm{t}}}} {{{\left( {\mu \lambda _i^{ - 1} - \frac{1}{{{{\left| {{{\mathit{\boldsymbol{\bar h}}}_i}{\mathit{\boldsymbol{w}}_i}} \right|}^2}}}} \right)}^ + } = P} } $

(11)

该公式化问题实际上是寻找2个二进制整数集，实现基站发射天线和小区用户的最优折中，减少系统硬件复杂度.关于此类联合天线选择与用户调度算法系统性能最优的为简单匹配(BFS, brute force search)算法，但当天线数目较大时，其计算复杂度过高，无法在系统中实现数据的实时处理，从而在现实中无法实施.所以针对此问题提出一种复杂度较低的能够更好地实现系统性能与硬件复杂度的折中，且计算复杂度较低的贪婪算法.

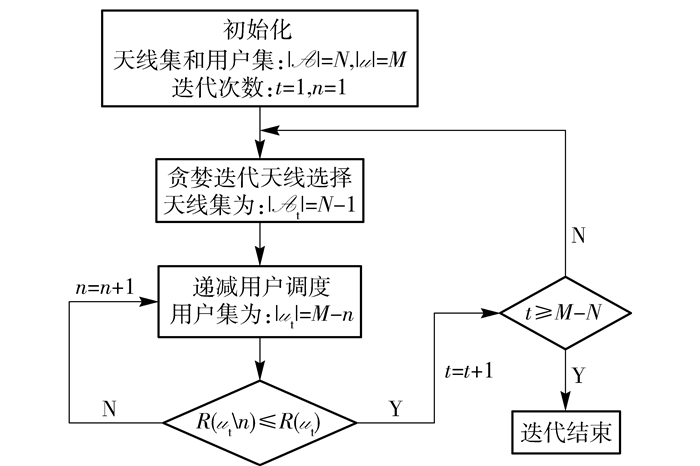
2 大规模MIMO系统联合算法

提出一种适用于大规模MIMO系统下行链路的联合天线选择和递减用户调度方案. 图 2为流程图.首先进行贪婪迭代天线选择，在该天线集的基础上进行递减用户选择，通过分别利用基站发射天线选择和用户调度提高的空间选择性增益和多用户分集增益实现.算法实现的关键是在每次迭代过程中删除一个最“差”的天线，该天线对系统性能贡献最小或者可能导致系统性能下降.在每次迭代时，小区端通信用户会发生变化，通过递减用户调度算法选择出一个最优的用户集以使系统能够达到更高的总速率.

2.1 天线选择

天线选择需要经过(M-N)次迭代处理，在每次迭代的过程中删除一个最“差”的天线，该天线的移除满足能够使系统的总速率达到最大.对于最“差”天线的选择为一个贪婪选择过程，计算出逐次删除一个天线后的总速率，选择使总速率最大时移除的天线，即为最“差”的天线.算法1如下.

算法1  联合天线选择与用户调度算法

输入：

信道状态矩阵H=[h₁^H, h₂^H, …, h_X^H]^H；

RF链路数量N；

初始化：t=1；A={1, 2, …, M}；

迭代过程：

1    for t=1:(M-N)

2    maxRate←0；

3   for each m in A do

4    U_t←a set of users from table 2 or 3 (A\{m}, N)；

5       R_-m=R_sum(A, U_t)；

6     If R_-m > maxRate then

7         maxRate←R_-m；

8         m_bad←m；

9         U←U_t

10      end

11    end

12  A←A\{m_bad}；

13   end输出：选择天线集A，调度用户集U.

该选择过程得到选择天线集A和调度用户集U两个集合.选择的天线数N是固定的，即RF链路数量已定，硬件复杂度较低.初始化选择天线集为全部天线，在每次迭代过程中依次移除一个天线，迭代完所有天线元素后，经比较，删除某天线能够使系统性能提高最明显，则定义该天线为最差天线，并删除，即A_t\{m_bad}.采用依次移除的贪婪迭代，次数为(M-N).当RF链路数有限时，通过用户选择算法调度系统中信道条件较好的用户，使系统能够达到更高的容量.

2.2 递减用户选择

ZF波束成形使得基站与用户之间信道相互正交，能够完全消除其他用户对目标用户的干扰.删除用户n后，待选择用户集U_t会发生变化，新的待选用户集更新为U_t\{n}，其对应的有效信道增益向量同样会随之更新. ZF波束成形矩阵由文献[6]中的有效信道增益向量v_i定义可得

$ {\mathit{\boldsymbol{v}}_i} = {\mathit{\boldsymbol{h}}_i}\mathit{\boldsymbol{P}}_i^ \bot $

(12)

$ {\mathit{\boldsymbol{w}}_i} = \frac{{\mathit{\boldsymbol{v}}_i^{\rm{H}}}}{{{{\left\| {{\mathit{\boldsymbol{v}}_i}} \right\|}^2}}} $

(13)

$ \mathit{\boldsymbol{P}}_i^ \bot = {\mathit{\boldsymbol{I}}_{\left| {{\mathit{A}}_\text{t}} \right|}} - \mathit{\boldsymbol{H}}_{_{{{A_{\rm{t}}}},{{U_{\rm{t}}}}\backslash \left\{ i \right\}}}^{\rm{H}}{\left( {{\mathit{\boldsymbol{H}}_{_{{{A_{\rm{t}}}},{{U_{\rm{t}}}}\backslash \left\{ i \right\}}}}\mathit{\boldsymbol{H}}_{_{{{A_{\rm{t}}}},{{U_{\rm{t}}}}\backslash \left\{ i \right\}}}^{\rm{H}}} \right)^{ - 1}}{\mathit{\boldsymbol{H}}_{_{{{A_{\rm{t}}}},{{U_{\rm{t}}}}\backslash \left\{ i \right\}}}} $

为子空间V_i=span{h_j|j∈U_t, j≠i}的正交投影算子，有效信道增益λ_i=‖v_i‖². I_|At|表示为|A_t|×|A_t|的单位矩阵，更新的有效信道增益向量为

$ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\tilde v}}}_i}\mathit{\boldsymbol{ = }}{\mathit{\boldsymbol{h}}_i}\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{v}}_i^{\rm{H}}}&{\mathit{\boldsymbol{v}}_n^{\rm{H}}} \end{array}} \right]{{\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{v}}_i}\mathit{\boldsymbol{v}}_i^{\rm{H}}}&{{\mathit{\boldsymbol{v}}_i}\mathit{\boldsymbol{v}}_n^{\rm{H}}}\\ {{\mathit{\boldsymbol{v}}_n}\mathit{\boldsymbol{v}}_i^{\rm{H}}}&{{\mathit{\boldsymbol{v}}_n}\mathit{\boldsymbol{v}}_n^{\rm{H}}} \end{array}} \right]}^{ - 1}}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{v}}_i}}\\ {{\mathit{\boldsymbol{v}}_n}} \end{array}} \right] = }\\ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{h}}_i}\mathit{\boldsymbol{v}}_i^{\rm{H}}}&0 \end{array}} \right]\frac{1}{{{{\left\| {{\mathit{\boldsymbol{v}}_i}} \right\|}^2}{{\left\| {{\mathit{\boldsymbol{v}}_n}} \right\|}^2} - {{\left\| {{\mathit{\boldsymbol{v}}_i}\mathit{\boldsymbol{v}}_n^{\rm{H}}} \right\|}^2}}} \times }\\ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{v}}_n}\mathit{\boldsymbol{v}}_n^{\rm{H}}}&{ - {\mathit{\boldsymbol{v}}_i}\mathit{\boldsymbol{v}}_n^{\rm{H}}}\\ { - {\mathit{\boldsymbol{v}}_n}\mathit{\boldsymbol{v}}_i^{\rm{H}}}&{{\mathit{\boldsymbol{v}}_i}\mathit{\boldsymbol{v}}_i^{\rm{H}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{v}}_i}}\\ {{\mathit{\boldsymbol{v}}_n}} \end{array}} \right] = }\\ {\frac{{{{\left\| {{\mathit{\boldsymbol{v}}_i}} \right\|}^2}{{\left\| {{\mathit{\boldsymbol{v}}_n}} \right\|}^2}}}{{{{\left\| {{\mathit{\boldsymbol{v}}_i}} \right\|}^2}{{\left\| {{\mathit{\boldsymbol{v}}_n}} \right\|}^2} - {{\left\| {{\mathit{\boldsymbol{v}}_i}\mathit{\boldsymbol{v}}_n^{\rm{H}}} \right\|}^2}}}\left( {{\mathit{\boldsymbol{v}}_i} - \frac{{{\mathit{\boldsymbol{v}}_i}\mathit{\boldsymbol{v}}_n^{\rm{H}}}}{{{{\left\| {{\mathit{\boldsymbol{v}}_n}} \right\|}^2}}}{\mathit{\boldsymbol{v}}_n}} \right)} \end{array} $

(14)

所以，有效信道增益及有效信道增益向量为

$ \begin{array}{l} {{\tilde \lambda }_i} = \mathit{\boldsymbol{\tilde v}}_i^2 = {\lambda _i}\frac{{{{\left\| {{\mathit{\boldsymbol{v}}_i}} \right\|}^2}{{\left\| {{\mathit{\boldsymbol{v}}_n}} \right\|}^2}}}{{{{\left\| {{\mathit{\boldsymbol{v}}_i}} \right\|}^2}{{\left\| {{\mathit{\boldsymbol{v}}_n}} \right\|}^2} - {{\left\| {{\mathit{\boldsymbol{v}}_i}\mathit{\boldsymbol{v}}_n^{\rm{H}}} \right\|}^2}}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\lambda _i^2{\lambda _n}}}{{{\mathit{\lambda }_i}{\lambda _n} - {{\left\| {{\mathit{\boldsymbol{v}}_i}\mathit{\boldsymbol{v}}_n^{\rm{H}}} \right\|}^2}}} \end{array} $

(15)

$ {{\mathit{\boldsymbol{\tilde v}}}_i} = \frac{{{\lambda _i}{\lambda _n}}}{{{\lambda _i}{\lambda _n} - {{\left\| {{\mathit{\boldsymbol{v}}_i}\mathit{\boldsymbol{v}}_n^{\rm{H}}} \right\|}^2}}}\left( {{\mathit{\boldsymbol{v}}_i} - \frac{{{\mathit{\boldsymbol{v}}_i}\mathit{\boldsymbol{v}}_n^{\rm{H}}}}{{{\lambda _n}}}{\mathit{\boldsymbol{v}}_n}} \right) $

(16)

将$ {\mathit{\boldsymbol{w}}_\mathit{i}}\frac{{\mathit{\boldsymbol{v}}_\mathit{i}^{\rm{H}}}}{{{{\left\| {{\mathit{\boldsymbol{v}}_\mathit{i}}} \right\|}^2}}}$，λ_i=‖v_i‖²代入式(15)(16) 可得

$ {{\tilde \lambda }_i} = \frac{{{\lambda _i}}}{{1 - {\lambda _n}{\lambda _i}{{\left| {\mathit{\boldsymbol{w}}_n^{\rm{H}}{\mathit{\boldsymbol{w}}_i}} \right|}^2}}} $

(17)

$ {{\mathit{\boldsymbol{\tilde w}}}_i} = {\mathit{\boldsymbol{w}}_i} - {\lambda _n}\mathit{\boldsymbol{w}}_n^{\rm{H}}{\mathit{\boldsymbol{w}}_i}{\mathit{\boldsymbol{w}}_n} $

(18)

递减用户选择算法步骤如下.

算法2  递减用户调度算法

输入：

由表 1得到的天线集A_t=A\{m}；

初始化：U←{1, 2, …, X}; W=H^H(HH^H)^-1；

$ \mathit{\lambda = }\left[ {\frac{1}{{{{\left\| {{\mathit{\boldsymbol{w}}_1}} \right\|}^2}}},\frac{1}{{{{\left\| {{\mathit{\boldsymbol{w}}_2}} \right\|}^2}}}, \cdots ,\frac{1}{{{{\left\| {{\mathit{\boldsymbol{w}}_X}} \right\|}^2}}}} \right]; $

迭代过程：

1    for i=1:X

2     for each k in U

3      $ \mathit{n}{\rm{ = arg}}\;\mathop {{\rm{min}}{\mathit{\lambda }_\mathit{k}}}\limits_{\mathit{k} \in \mathit{U}} $；

4    end

5   if ΔR=R(U\n)-R(U)≥0,

6      U←U\{n}；

7      for each k in U

8         $ {\mathit{\boldsymbol{w}}_\mathit{k}} \leftarrow {\mathit{\boldsymbol{\tilde w}}_\mathit{k}}{\rm{ = }}{\mathit{\boldsymbol{w}}_\mathit{k}}{\rm{ - }}{\mathit{\lambda }_\mathit{n}}\mathit{\boldsymbol{w}}_\mathit{n}^{\rm{H}}{\mathit{\boldsymbol{w}}_\mathit{i}}{\mathit{\boldsymbol{w}}_\mathit{n}}$；

9         $ {\mathit{\lambda }_\mathit{k}} \leftarrow {\mathit{\tilde \lambda }_\mathit{k}}{\rm{ = }}\frac{{{\mathit{\lambda }_\mathit{k}}}}{{{\rm{1 - }}{\mathit{\lambda }_\mathit{n}}{\mathit{\lambda }_\mathit{k}}{\rm{|}}\mathit{\boldsymbol{w}}_\mathit{n}^{\rm{H}}{\mathit{\boldsymbol{w}}_\mathit{k}}{{\rm{|}}^{\rm{2}}}}}$；

10    end

11   end

12  end

13   U_t←U；

输出：算法1所需的调度用户集U_t

首先选择全部用户，然后依次迭代删除使系统性能降低的用户.利用式(17) 和式(18) 更新被选用户集U_t、有效信道增益以及波束成形矩阵W.计算复杂度主要集中在波束成形向量的求解上，即信道矩阵的求逆，利用公式可以减少矩阵的求逆，从而减少计算复杂度.该算法计算复杂度较低，且性能相对较优，但性能略差于BFS.

算法3  半正交用户调度算法步骤

输入：

由表 1得到的天线集A_t=A\{m};

正阈值α;

初始化：

$ \begin{array}{l} U \leftarrow \left\{ {1,2, \cdots ,X} \right\};\\ {\mathit{U}_{\rm{t}}} = \varnothing ; \end{array} $

迭代过程：

1   for i=1: X

2    for each k in U do

3     $ {\mathit{\boldsymbol{g}}_{\mathit{k}{\rm{, }}\mathit{A}}}{\rm{ = }}{\mathit{\boldsymbol{\bar h}}_{\mathit{k}{\rm{, }}\mathit{A}}}{\rm{ - }}\sum\limits_{\mathit{j} = 1}^{\mathit{i} - 1} {\frac{{{{\mathit{\boldsymbol{\bar h}}}_{\mathit{k}{\rm{, }}\mathit{A}}}\mathit{\boldsymbol{\tilde g}}_\mathit{j}^{\rm{H}}{{\mathit{\boldsymbol{\tilde g}}}_\mathit{j}}}}{{{{\left\| {{{\mathit{\boldsymbol{\tilde g}}}_\mathit{j}}} \right\|}^2}}}} $;

4    end

5     $ {\mathit{i}_{{\rm{opt}}}} = \arg \;\mathop {\max }\limits_{\mathit{k} \in \mathit{U}} \left\| {{\mathit{\boldsymbol{g}}_{\mathit{k}{\rm{, }}\mathit{A}}}} \right\|$；

6    U_t←U_t∪{i_opt}；

7    U←U\U_t；

8     $ {{\mathit{\boldsymbol{\tilde g}}}_\mathit{i}}$=g_iopt；

9   if |U_t| < X

10     $ \mathit{U} \leftarrow \left\{ {\mathit{k} \in \mathit{U}{\rm{, }}\mathit{k} \ne {\mathit{i}_{{\rm{opt}}}}{\rm{|}}\frac{{\left| {{{\mathit{\boldsymbol{\bar h}}}_\mathit{k}}\mathit{\boldsymbol{\tilde g}}_\mathit{j}^{\rm{H}}} \right|}}{{\left\| {{{\mathit{\boldsymbol{\bar h}}}_\mathit{k}}} \right\|\left\| {{{\mathit{\boldsymbol{\tilde g}}}_\mathit{j}}} \right\|}}{\rm{ < }}\mathit{\alpha }} \right\}$

11   end

12  end

输出：算法1所需要的调度用户集U_t

算法3为半正交用户选择算法^[7]的改进.联合天线选择与半正交用户调度(JAS-SUS, joint antenna selection and semi-orthogonal user scheduling)^[7]算法要求RF链路数与小区调度用户数均已定，且保持相同的关系.为选择能够提高系统总速率的用户，对系统性能有负作用的用户则被移除，不固定用户数量.首先计算U_t集合内所有用户的g_i，比较其2-范数，选择出2-范数最大的一个用户为当前迭代过程的最优用户i_opt，然后利用第9~11行的阈值α排除部分信道条件较差的用户，缩小可选用户范围，减少迭代的次数.每次迭代过程选择出信道条件较好的用户组成调度用户集U.该过程初始化状态为g_i=h_i.

3 计算复杂度

联合天线选择与递减用户调度方案的计算复杂度主要在于贪婪天线选择的过程中.在删除天线的过程中，当准备删除第i个天线时，需要进行M-i+1次贪婪比较.而在用户调度的过程中计算复杂度主要在于波束成形矩阵的初始化过程中.

广义矩阵的求逆复杂度为O(M_tM_r²)^[8]，其中M_t表示发射天线数，M_r表示接收用户数.在第i次贪婪过程中要进行(M+1-i)次用户调度，而在用户调度过程中天线数为(M-i)，用户数为X，所以波束成形求逆中的复杂度为(M-i)X².此过程的计算复杂度为(M-i)(M+1-i)X².

另外在第i次迭代过程中，递减用户调度的复杂度在于初始化计算有效信道增益λ_i，为X个(M+1-i)×1的列向量的2-范数求解，复杂度为X(M+1-i)，以及|U_t|-1个向量相乘以及|U_t|-1个2-范数求解，每次迭代包括2(M+1-i)(|U_t|-1) 个乘法.其总的复杂度为

$ \begin{array}{*{20}{c}} {X\left( {M + 1 - i} \right) + \sum\limits_{n = \left| {\mathit{U}_{\rm{t}}} \right|}^K {2\left( {M + 1 - i} \right)\left( {n - 1} \right) \ll } }\\ {X\left( {M + 1 - i} \right) + \sum\limits_{n = 1}^K {2\left( {M + 1 - i} \right)\left( {n - 1} \right) \ll } }\\ {\left( {M + 1 - i} \right){X^2}} \end{array} $

因为要删除(M-N)个天线，故联合天线选择与用户调度算法的总计算复杂度

$ \sum\limits_{i = 1}^{M - N} {\left( {M - i} \right)\left( {M + 1 - i} \right){X^2}} $

表 1总结了当RF链路数与调度用户数一定情况下，不同的联合算法的计算复杂度.可明显地看出，相同情况下所需乘法器个数较大的为BFS，其复杂度数量级远远大于其他联合算法.而相对复杂度最低的即为JAS-DUS，其计算复杂度相对于JAS-SUS、联合天线选择与迫零调度(JAS-ZFS，joint antenna selection and zero-forcing scheduling)来说要低1~2个数量级，而相对于BFS来说，随着天线数与用户数的增加，JAS-DUS则降低了几十个数量级.由此可以看出，JAS-DUS更适用于实际大规模MIMO系统.

4 仿真结果

采用蒙特卡洛仿真对BFS、JAS-SUS、JAS-ZFS以及所提的JAS-DUS算法进行性能比较.假设场景为单小区，基站配置大规模天线，在小区内有大量单天线用户.由于BFS算法的计算复杂度较高，MATLAB较难处理，限制了参数，使基站天线数和小区用户数略低.

图 3为不同信噪比情况下的总速率，由图中可以看出BFS的性能最高. JAS-ZFS性能与所提JAS-DUS性能大致相同，但其计算复杂度较高.

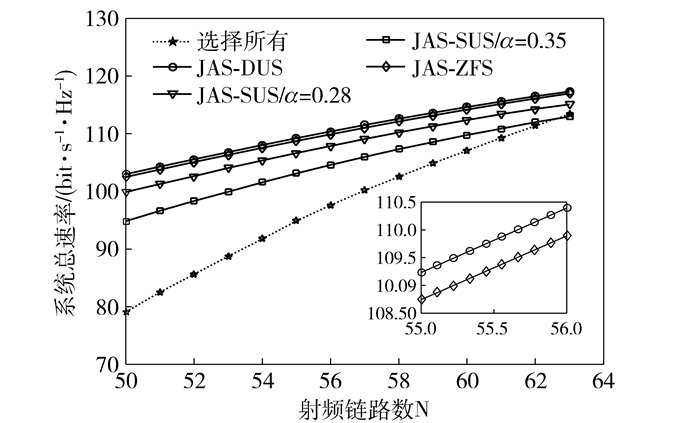
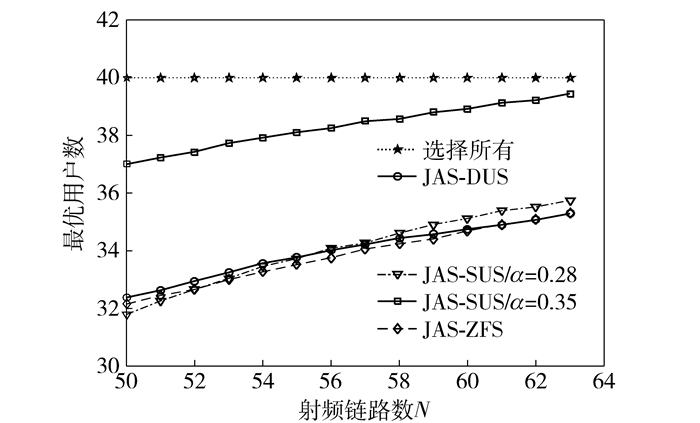
当RF链路数目已定，为了最大化系统总速率，需要同时移除较“差”的用户和天线，图 4、图 5场景参数相同，基站天线数M=64，用户数X=40，可以看出，经过天线选择和用户调度后，随着RF链路数的增加，系统性能有所增加.当RF链路数基本上等于基站天线数时，选择小区内信道状态较优的用户作为信号接收端，所提的基于联合天线选择和递减用户调度算法性能略高于JAS-ZFS，且明显高于JAS-SUS，而JAS-SUS与阈值α有很大的关系.由图可以看出随着α的增加，系统移除的“差”的用户较少，可调度用户比较多，导致性能较低.当RF链路数较大时，天线选择现象不明显，算法之间仅存在些许由用户调度算法的不同而引起的差异.

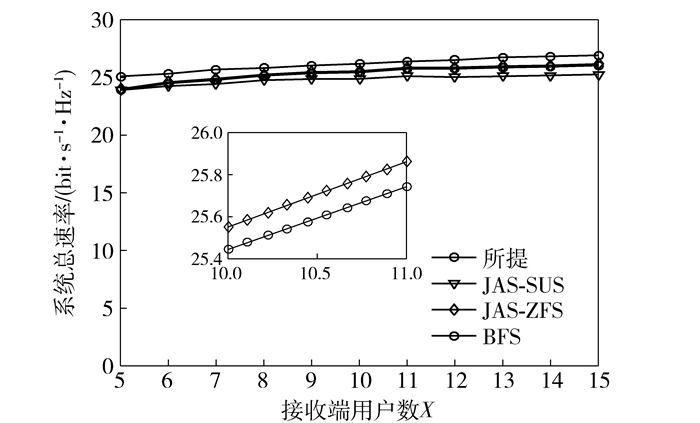
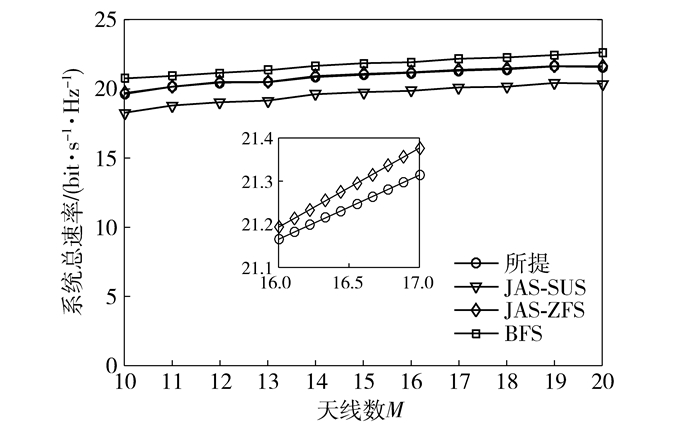
由图 6、图 7可以看出RF链路与调度用户数一定情况下天线数与用户数的变化，系统总速率变化较小.

5 结束语

在大规模MIMO系统中，基站天线数与用户数很大，系统硬件复杂度随之也较大，损耗的功率同样较大.联合天线选择与递减用户调度算法在RF链路一定的情况下，选出信道状态较好的天线以及用户，提高了系统的总速率.仿真结果证明，联合天线选择与用户调度算法能够在保证系统性能的前提下降低系统硬件复杂度.