2. 西安交通大学 软件学院, 西安 710049
在软件定义网络中提出了一种应用蚁群优化的负载均衡算法,以负载均衡度为目标函数重定义了蚁群算法中的参数和操作,对软件定义网络数据流和网络拓扑进行合理设置,规划出流传输的最优路径,从而提升了网络资源利用率和流传输质量.仿真结果表明,与其他算法相比,新算法在负载均衡度、流接受率、流丢包率、时延以及网络吞吐量方面的性能都有明显的提升.
2. School of Software Engineering, Xi'an Jiaotong University, Xi'an 710049, China
An ant colony optimization-based load balancing alogrithm was proposed in software defined network. This alogrithm defines the degree of load balancing as the objective function and redefines the parameters and operations in the ant colony algorithm. The software defined network flows and the network topology are designed reasonably. The optimal paths of software defined network flows are derived from thealogrithm, which promotes the network resource utilization and transmission quality. Simulations show that the proposed alogrithm outperforms the benchmark algorithm in terms of the degree of load balancing, flow acceptance rate, packet loss rate, delay and network throughput.
负载均衡通过合理的网络资源来扩展网络对数据的传输处理能力,从而避免网络拥塞,提高网络的性能和鲁棒性[1].与传统IP网络相比,软件定义网络(SDN, software defined network)负载均衡具有对全局拓扑进行感知,动态实施负载均衡,可编程扩展的优势.
现有文献对SDN负载均衡的研究存在如下问题:1) 网络拓扑规模小或结构单一,流划分粒度粗,设置缺乏合理性[2-4];2) 未充分利用SDN集中控制和可编程性优势[5-6];3) 负载均衡时,每次可供选择的路径少,不能达到最优效果[7-8].
笔者对上述问题做出改进,提出了蚁群优化的负载均衡(LB-ACO, ant colony optimization-based load balancing)算法,① 对流的到来和离开以及种类进行合理设置,应用场景广泛;② 充分利用SDN集中控制的全局视图,实时获取网络状态并通过调整时间窗来控制算法调用频率;③ 通过SDN可扩展性优势,将算法移植到开源控制器上,来验证算法的实用性.
1 问题描述和评价指标 1.1 问题描述现有的OpenFlow控制器系统提供了简单的完成数据流转发的模块,如FloodLight中的路由算法使用Dijstra算法通过计算源节点到目的节点的最短跳数,来规划路径控制数据流的转发.前k条最短路径(KSP,top-k shortest path distance)算法的目的是寻找起点到终点的多条路径,形成最短路径组,以满足对路径的需求[9],KSP算法是Dijkstra算法的延伸,k值越大,最短路径组规模越大,算法的复杂度也越高,当k=1时,退化为Dijkstra算法[10].当网络拓扑比较简单或以找到路径为目标时,k最短路径有较好的效果.而当网络拓扑较复杂,求解目标为全局的负载均衡度时,由于KSP算法路径选择多样性差.随着网络流的增加,链路负载不均衡性越来越严重,进而造成网络流丢包率和延迟上升以及吞吐量下降等网络性能问题.为此,以提高网络链路均衡和流传输质量为目标,设计了针对网络流的路径分配策略.蚁群优化算法在寻路问题上应用广泛,同时其自组织性和正反馈性也使得算法具有环境适应能力强、收敛性佳的优点.将蚁群算法用于控制器的路径选择,利用其群体智能性来规划路径,可提高网络链路的负载均衡度和流传输质量.
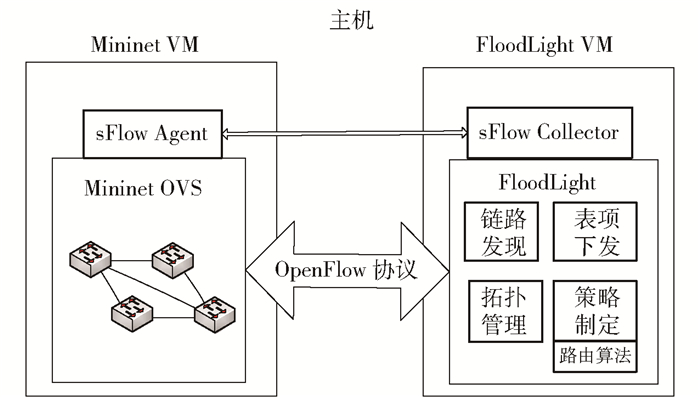
1.2 设计框架使用开源控制器FloodLight和底层网络设备Mininet分别模拟数据平面和控制平面,控制器通过sFlow流量采集工具和链路发现协议获取底层拓扑状态,由LB-ACO算法制定转发策略来指导数据流的传输,从而达到提升网络性能的目的.设计框架如图 1所示.
|
图 1 设计框架 |
底层网络设备Mininet是由Stanford大学Nick McKeown研究小组基于Linux Container架构研究开发的一个轻量级软件定义网络研发和测试平台[3]. FloodLight是支持Apache协议的企业级OpenFlow控制器,与NOX、POX等其他控制器类似,也使用了“层次化”架构来实现控制功能,同时提供了丰富的应用,可直接在网络中部署数据转发、拓扑发现等基本功能,通过向OpenFlow交换机下发流表等方式来实现数据分组转发决策,以达到对交换设备集中控制的目的.流量采集工具sFlow是一种以设备为基本数据单元的数据流随机采样流量监控技术,能详细、实时地分析网络传输流的性能、趋势及问题.其由嵌入到交换机负责周期数据采样的sFlow Agent和负责对采样数据分析、汇总的sFlow Collector组成. sFlow功能如下:对底层网络进行周期性数据采样,感知当前网络的链路状态;为负载均衡算法和路径选择提供数据支持.
设置流表项存活时间,决定控制器规划路径的频率,对到来的数据流进行处理,步骤如下.
1) 数据流到来时,解析数据包信息来匹配Mininet OVS中流表项,进行转发;
2) 若不匹配,通过OpenFlow协议,将其数据包信息发送给FloodLight控制器;
3) 控制器调用路由算法,根据实时链路信息和数据包信息,来制定转发策略,确定流表项;
4) 通过OpenFlow协议将流表项下发到数据平面来指导流的传输.
1.3 评价指标从网络性能和流传输质量两个方面对算法进行评估,评估指标如下:
1) 链路负载均衡度
| $ {\mathit{L}_{\rm{B}}}\left( \mathit{t} \right){\rm{ = }}\sqrt {{{\sum\limits_{\mathit{i} = 1}^\mathit{n} {\sum\limits_{\mathit{j} = \mathit{i}}^\mathit{n} {\left( {{\mathit{l}_{\mathit{cij}}}{\rm{ - }}\frac{{\sum\limits_{\mathit{i} = 1}^\mathit{n} {\sum\limits_{\mathit{j} = \mathit{i}}^\mathit{n} {{\mathit{l}_{\mathit{cij}}}} } }}{\mathit{m}}} \right)} } }^2}} $ | (1) |
其中:n为节点数,lcij为链路(i, j)的当前带宽,m为拓扑中链路数.
2) 网络流接受率
| $ {\mathit{F}_{\rm{A}}}\left( \mathit{t} \right){\rm{ = }}\frac{{{\mathit{f}_{\rm{s}}}\left( \mathit{t} \right){\rm{}}}}{{{\mathit{f}_{\rm{c}}}\left( \mathit{t} \right)}} $ | (2) |
其中:fs(t)为截止到当前时刻,成功接受的流数,fc(t)为截止到当前时刻,共发送的流数.
3) 网络带宽占用率
| $ {\mathit{B}_{\rm{P}}}{\rm{ = 1 - }}\frac{{\sum\limits_{\mathit{i} = 1}^\mathit{n} {\sum\limits_{\mathit{j} = \mathit{i}}^\mathit{n} {{\mathit{l}_{\rm{c}}}} } }}{{\sum\limits_{\mathit{i} = 1}^\mathit{n} {\sum\limits_{\mathit{j} = \mathit{i}}^\mathit{n} {{\mathit{l}_{\rm{p}}}} } }} $ | (3) |
其中lp, ij为初始时链路(i, j最大带宽容量).
4) 网络吞吐量
| $ {\mathit{T}_{\rm{R}}}{\rm{ = }}\mathop {\lim }\limits_{\mathit{t} \to \infty } {\mathit{f}_{\rm{s}}}\left( \mathit{t} \right) $ | (4) |
其中TR为网络流持续时间无限长时,网络拓扑能成功发送的最大流数目.
5) 流丢包率和流时延.即网络流在传输过程中的丢包率和延迟的时间.
2 应用LB-ACO算法 2.1 蚁群算法基础ACO算法是一种模拟蚂蚁觅食行为的模拟优化算法,由DorigoM等[11]首先提出.该算法对自然界蚂蚁的寻径方式进行模拟,蚂蚁在运动过程中,能够在其经过的路径上留下外激素进行信息传递,且在运动过程中能够感知之中物质,以此指导自身的运动方向.因此,大量蚂蚁组成的蚁群集体行为表现出一种信息正反馈现象,某条路径上走过的蚂蚁越多,后者选择该路径的概率就越大.基本蚁群算法描述如下.蚂蚁的状态转移概率为
| $ \mathit{p}_{\mathit{ij}}^\mathit{k}\left( \mathit{k} \right){\rm{ = }}\frac{{{{{\rm{[}}{\mathit{\tau }_{\mathit{ij}}}\left( \mathit{t} \right){\rm{]}}}^\mathit{\alpha }}{{{\rm{[}}{\mathit{\eta }_{\mathit{ik}}}\left( \mathit{t} \right){\rm{]}}}^\mathit{\beta }}}}{{\sum\limits_{\mathit{s} \in {\rm{allowe}}{{\rm{d}}_\mathit{k}}} {\left[{{\mathit{\tau }_{\mathit{is}}}{{\left( \mathit{t} \right)}^\mathit{\alpha }}{{\left[{{\mathit{\eta }_{\mathit{is}}}\left( \mathit{t} \right)} \right]}^\mathit{\beta }}} \right]} }} $ | (5) |
其中:α为信息素启发因子,值越大表示蚂蚁越倾向于选择之前蚂蚁选择的路径,蚂蚁之间的协作性越强;β为期望启发式因子,值越大表示启发信息越受重视,τij(t)为路径(i, j)上信息素;ηik(t)为第k只蚂蚁下一跳的创新因子;allowedk为第k只蚂蚁的下一跳的候选节点集.蚂蚁的信息素更新公式为
| $ {\mathit{\tau }_{\mathit{ij}}}\left( {\mathit{t}{\rm{ + }}\mathit{n}} \right){\rm{ = }}\left( {{\rm{1 - }}\mathit{\rho }} \right){\mathit{\tau }_{\mathit{ij}}}\left( \mathit{t} \right){\rm{ + }}\sum\limits_{\mathit{k} = 1}^\mathit{m} {{\rm{\Delta }}\mathit{\tau }_{\mathit{ij}}^\mathit{k}\left( \mathit{t} \right)} $ | (6) |
其中:ρ为信息素的挥发系数,以防止信息素的无限积累.信息素的Ant-Cycle更新策略为
| $ {\rm{\Delta }}\mathit{\tau }_{\mathit{ij}}^\mathit{k}{\rm{ = }}\frac{\mathit{Q}}{{\sum {{\mathit{L}_\mathit{k}}} }}{\rm{, }}\;{\rm{0 < }}\mathit{k} \le \mathit{A} $ | (7) |
其中:Lk为第k只蚂蚁在本次循环中所走路径的总长度,A为蚁群规模.
2.2 蚁群算法参数及操作的重定义定义1(信息素更新) 信息素定义为网络链路空闲率和路径跳数的均衡值,保证蚂蚁倾向于选择链路空闲率更高和路径跳数更少的路径;信息素的更新策略可保证蚂蚁群体的互相影响,通过群体智能性选择最优路径. ρ=0.3,经测试在0.2~0.4范围内,算法的路径搜索能力和收敛性能都比较好.
定义2(启发函数) 启发函数根据路径信息素的值设置,在一定范围内随机选择数值,保证蚂蚁在选择路径时不单纯依靠信息素,而是有一定的“创新性”,防止算法陷入局部最优.
定义3(启发因子) α=3,β=2;在启发因子的选择过程中,当α/β过大时,蚂蚁在进行路径选择时会高度依赖信息素,容易陷入局部最优;当α/β过小时,蚂蚁选择路径的随机性较大,没有更好的汲取其他蚂蚁的“经验”,收敛速度下降,且不容易找到最优解.
2.3 蚁群算法解决负载均衡问题LB-ACO算法以网络拓扑的负载均衡度为适应度函数,对源节点每次到达的流进行路径选择,蚂蚁的路径优化选择即为确定流由源地址到目的地址的最佳路径算法步骤如下.
步骤1 初始化网络拓扑和流事件.网络拓扑节点数为N,链路数为L,链路带宽最大值和最小值分别为Lmax和Lmin,流事件单流数为X,多流数为Y,到来的泊松分布参数为λ,流持续的寿命分布参数为γ,每条流的源地址为S,目的地址为D.
步骤2 初始化蚁群算法参数.蚂蚁规模为A,蚂蚁初始位置为L, 网络拓扑初始信息素为τ,最大寻找次数为Fmax,算法迭代数为I.
步骤3 对到来的流事件使用蚁群算法,蚂蚁根据状态转移式(5),选择下一个节点.
步骤4 判断选择的节点是否在D中,若是则将源节点到此节点的路径存储在路径序列R中;否则判断寻找次数是否小于Fmax,是则选择下一个节点,否则执行步骤6.
步骤5 根据式(1),选择最合适的路径,根据式(6) 和式(7) 更新信息素.
步骤6 检查迭代数,如果小于I,执行步骤3,否则执行步骤7.
步骤7 输出本次流事件路径,更新网络拓扑负载.
3 实验性能分析和评估从负载均衡度、流接收率、带宽占用率、吞吐量、时延和丢包率6个方面对算法性能进行分析,并与参考文献[3-4]中的所使用的KSP算法进行对比. KSP算法中k=5,其中多流时延和丢包率仿真数据为本次流数据的均值.
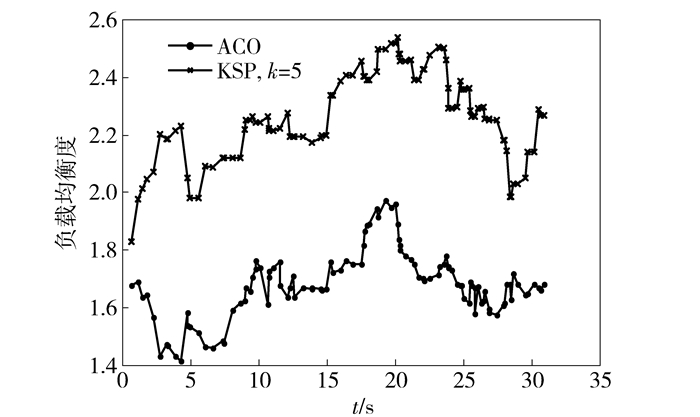
网络流传输过程中负载均衡度如图 2所示.负载均衡值越低表示网络中链路负载越均衡.由图 2可见,LB-ACO算法在负载均衡方面明显优于KSP算法.初始时刻,网络拓扑中链路带宽不均等,负载均衡度约为1.81,随着网络流的到来,LB-ACO算法的负载均衡值降低,表示算法在规划流路径时优先考虑带宽值较大的链路,使链路可用负载值趋向均等,从而使网络链路负载更均衡;而KSP算法在规划路径时对链路负载均衡性考虑不到位,造成负载均衡值上升,使得链路更加不均衡.随着时间的增加,流事件的离开,网络中的负载均衡值逐渐恢复到初始时刻.流事件的到来和离开是离散的过程,因此负载均衡值的改变会发生突变,当遇到多流时突变值会更大.
|
图 2 负载均衡度 |
网络流在传输过程中流接收率的变化如图 3所示.由图 3可见,LB-ACO算法的性能比KSP算法高13.1%.当某条流到来时,通过算法不能规划出合适的路径时,就将该流舍弃.当曲线突然下降时,表示此流被舍弃;之后由于成功接受的流数和网络流的总数增加值相同,曲线值略微增加.整个网络流的传输过程中,LB-ACO算法共丢失5条流,而KSP丢失13条流.

|
图 3 流接受率 |
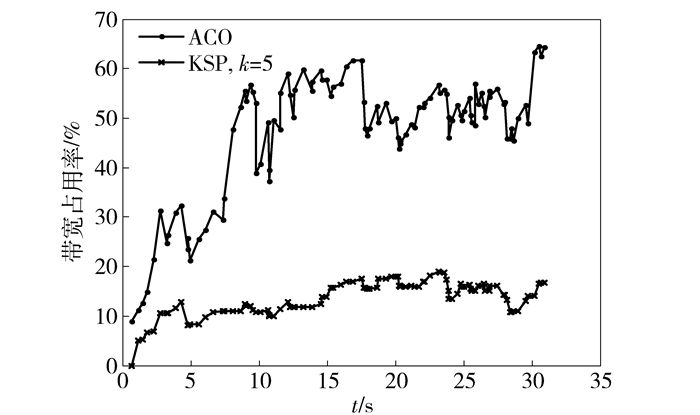
网络流的传输过程中,网络流链路占用率如图 4所示. LB-ACO算法占用更多的带宽,原因主要有:负载均衡算法是将流的传输分散在不同路径上,避免集中造成拥堵,流的分散必然导致流传输路径跳数增加,占用更多带宽;与LB-ACO算法相比,KSP算法丢失更多流,且这些流多为占用带宽较多的流,因此其带宽占用率更低.
|
图 4 带宽占用率 |
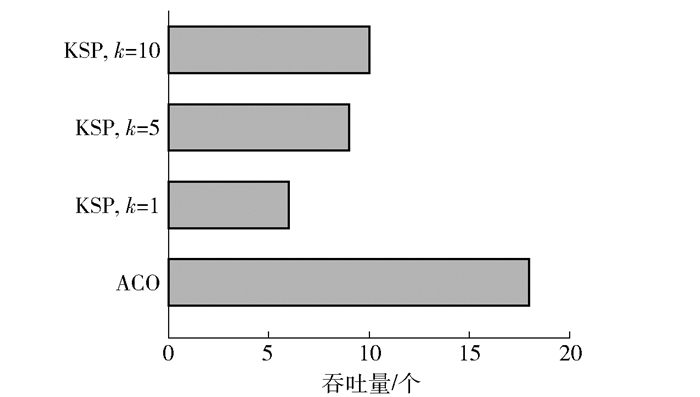
网络流在传输过程中,网络拓扑的吞吐量如图 5所示.由图 5可见,随着k值的增加,KSP算法吞吐量也有所上升,但上升的速度减缓.而由于路径选择的多样性,LB-ACO算法能够极大增加网络拓扑的吞吐量.
|
图 5 吞吐量 |
网络流在传输过程中,每条流的时延和丢包率对比分别如图 6和图 7所示.开始时,两者相差不大,随着流不断增加,LB-ACO算法对网络流的路径规划更加合理,因此拥堵的情况更少,从而降低了流的时延和丢包率.

|
图 6 时延 |

|
图 7 丢包率 |
负载均衡是提高网络资源利用率的重要手段,其目标值需要在全局网络拓扑下进行优化,而SDN的全局性优势为负载均衡性能的提升提供了契机. KSP算法在全局最优路径选择上,由于只选择前k条最短路径,随机性和多样性受限,通过增加算法的k值,固然能使性能有所提升,但同样也会增加算法的复杂度.相比之下,ACO算法由于自组织性和正反馈性的优点,能够在较低的时间复杂度下,向全局最优值收敛,是解决网络负载均衡的较好选择.
4 结束语以提高SDN中网络传输性能和流传输效率为目标,重定义ACO算法的参数、操作和适用度函数,实现基于蚁群算法的负载均衡优化.通过设计基于Mininet实验平台的网络模型,对流信息合理设置和分类,更新FloodLight控制平台的传统路由算法,来实现SDN平台下改进路由算法控制流传输的仿真.仿真结果表明,该算法能够充分利用SDN的集中控制和可扩展性优点,提高SDN下的链路负载均衡性、网络吞吐率和流接受率,并有效降低网络中的流时延和丢包率.
| [1] | 吴舢. 一种基于SDN的网络负载均衡方案的设计与实现[D]. 复旦大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10246-1015412360.htm |
| [2] |
曹傧, 刘勰, 孙奇. 软件定义网络架构下的动态自适应负载均衡策略研究[J]. 重庆邮电大学学报(自然科学版), 2015, 27(4): 460–465.
Cao Bin, Liu Xie, Sun Qi. Dynamically adaptive load balancing strategy under the software defined network structure[J]. Journal of Chongqing University of Posts and Telecommunications (Natural Science Edition), 2015, 27(4): 460–465. doi: 10.3979/j.issn.1673-825X.2015.04.005 |
| [3] | Dobrijevic O, Santl M, Matijasevic M. Ant colony optimization for QoE-centric flow routing in software defined networks[C]//International Conference on Network and Service Management.[S.l.]:IEEE, 2015:274-278. |
| [4] | Cui Chenxiao, Xu Yabin. Research on load balance method in SDN[J]. International Journal of Grid and Distributed Computing, 2016, 9(1): 25–36. doi: 10.14257/ijgdc |
| [5] | Long Hui, Shen Yao, Guo Minyi, et al. LABERIO:dynamic load-balanced routing in OpenFlow-enabled networks[C]//AINA 2013. Barcelona:IEEE, 2013:290-297. |
| [6] | Wang Yong, Tao Xiaoling, He Qian, et al. A dynamic load balancing method of cloud-center based on SDN[J]. China Communications, 2016, 13(2): 130–137. |
| [7] |
赵梦亚, 龙昭华, 蒋贵全, 等. 基于OpenFlow的负载均衡机制[J]. 计算机工程与设计, 2015, 36(9): 2356–2360.
Zhao Mengya, Long Zhaohua, Jiang Guiquan, et al. Load balancing mechanism based on OpenFlow[J]. Computer Engineering and Design, 2015, 36(9): 2356–2360. |
| [8] | Jain S, Kumar A, Mandal S, et al. B4:Experience with a globally-deployed software defined WAN[J]. ACM SIGCOMM Computer Communication Review, 2013, 43(4): 3–14. |
| [9] |
徐涛, 丁晓璐, 李建伏. K最短路径算法综述[J]. 计算机工程与设计, 2013, 34(11): 3900–3906.
Xu Tao, Ding Xiaolu, Li Jianfu. Review on K shortest paths algorithms[J]. Computer Engineering and Design, 2013, 34(11): 3900–3906. doi: 10.3969/j.issn.1000-7024.2013.11.036 |
| [10] |
白轶多, 胡鹏, 夏兰芳, 等. 关于k次短路径问题的分析与求解[J]. 武汉大学学报(信息科学版), 2009, 34(4): 492–494.
Bai Yiduo, Hu Peng, Xia Lanfang, et al. A kth-shortest path algorithm based on k-1 shortest paths[J]. Geomatics and Information Science of Wuhan University, 2009, 34(4): 492–494. |
| [11] | 段海滨. 仿生智能计算[M]. 北京: 科学出版社, 2011. |


