2. 北京科技大学 数理学院, 北京 100083
为了解决实际误差分布与假设误差分布不匹配导致最小二乘三维定位算法精度较低的问题,提出一种基于测距值优化的最小二乘室内三维定位算法.结合残差修正、Cayley-Menger行列式及空间四面体几何约束,利用非线性规划方法优化测距值,使测距误差符合高斯分布特性,从而提高最小二乘三维定位算法的定位精度.实验对比分析结果显示,所提算法具有较高的定位精度及稳定性.
2. School of Mathematics and Physics, University of Science and Technology, Beijing 100083, China
Least Square is a typical three-dimensional location algorithm for time of arrival based indoor positioning system. The precondition of traditional LS algorithm is that the measurement error meets the zero mean and the equal variance. However, the multipath and non-line of sight significant in realistic indoor environment leads TOA ranging error to be non-Gaussian distribution and cannot meet the hypothesis. This conflict leads low localization accuracy. This article presents a distance optimization based least square 3-D indoor localization algorithm. The nonlinear programming method with Cayley-Menger determinant and tetrahedral geometry constraints was adopted by the proposed algorithm to optimize measured distance, which makes the ranging error fit Gaussian distribution and thus improves the localization accuracy of least square. Experiments demonstrate that the proposed distance optimization based least square 3-D localization algorithm achieves better localization accuracy and stability.
无线室内定位技术在军事[1]、安防[2]、消防[3]、流程工业、健康监护、智能家居[4]等领域具有广泛应用.常用的无线定位技术包括基于接收信号强度(RSS, received signal strength)的室内定位技术、基于信号传播时间(TOA, time of arrival)的室内定位技术、基于信号传播时间差(TDOA,time difference of arrival)的室内定位技术、基于接收信号角度(AOA,angle of arrival)的室内定位技术.其中,TOA测距技术在超宽带(UWB,ultra-wide band)通信的基础上实现,具有较高的测量精度.
基于TOA的室内三维定位受到越来越多关注.常见的三维定位算法包括基于几何关系的三边测量算法[5],极大似然(ML, maximum likelihood)估计算法[6-8],最小二乘(LS, least squares)算法等.其中LS算法是最为常用的室内三维定位算法,其假设的测距误差模型为高斯分布,但实际室内TOA测距受到非视距传输和多径传输影响,测距误差总体上呈现非高斯性,这种非高斯误差导致原始的LS算法定位精度较差.因此,对LS算法的改进成为室内三维定位算法的一项重要研究内容.最常见的解决方式是对LS算法进行改进,从而适用于非高斯误差模型, 如加权最小二乘(WLS, weighted least squares)算法[9]、递归最小二乘定位算法[10].这类方法的挑战在于算法参数设置的依据较难确定.另一种方式是对测距值进行优化,减小实际误差分布和算法假设误差模型之间的差异,进而降低LS算法的定位误差,如文献[11]提出了利用Cayley-Menger行列式约束条件和非线性规划算法优化的测距值,然后使用LS算法求解位置坐标,该方法能提高定位精度.
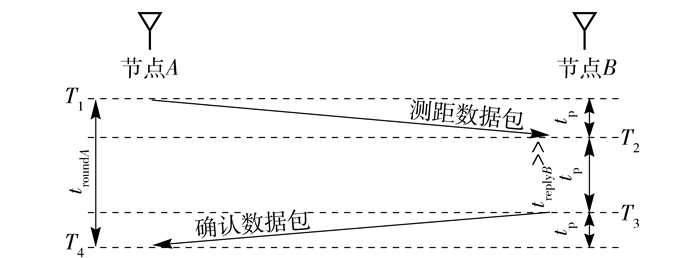
1.1 异步TOA测距原理TOA测距有同步和异步两种实现方式.同步方式要求发送和接收之间进行高精度的时钟同步,实现困难.而异步方式无需高精度的时钟同步,易于实现,是目前实现TOA测距的主要方法.异步TOA测距原理如图 1所示,节点A和节点B为进行TOA测距的两个节点. T1为节点A向节点B发送测距数据的时刻;T2为节点B收到测试数据的时刻;T3为节点B向节点A发送确认数据包的时刻;T4为节点A收到确认数据包的时刻.节点A和节点B通过本地时钟分别测量节点A发送测距数据包到收到确认数据包的时间长度(troundA)和节点B收到测距数据包到发出确认数据包的时间长度(treplyB),计算出信号在2个设备之间的传输时间tp.设备之间的测距值为
| $ \begin{array}{l} \hat d = {t_{\rm{p}}}C = \frac{{{t_{{\rm{round}}\mathit{A}}} - {t_{{\rm{reply}}\mathit{B}}}}}{2}C = \\ \;\;\frac{{\left( {{T_4} - {T_1}} \right) - \left( {{T_3} - {T_2}} \right)}}{2}C \end{array} $ | (1) |
|
图 1 异步TOA测距原理 |
其中C为光速.
1.2 室内TOA测距误差非高斯性TOA测距误差包括两方面:检测误差(εd),来自于硬件引入的脉冲波峰到达时间检测不准确;信号误差,来自于实际接收信号与理想接收信号之间的差异.其中室内环境造成的信号误差是TOA测距误差的主要来源.
视距传输(LOS, line of sight)和非视距传输(NLOS, non-line of sight)是室内环境中TOA测距的两种典型信号传输场景.在LOS场景中,发送端和接收端之间不存在遮档,测距误差主要由多径叠加导致脉冲波峰偏移造成;在NLOS场景中,发送端和接收端之间存在遮挡物,主要测距误差来自遮挡造成的直视路径信号不可测(UDP, undetectable direct path)的信道状况.因此,信号误差可看作由多径误差(εm)和UDP误差(εu)构成. εm来自于第一个可检测路径(FDP, first detectable path)脉冲与邻近路径脉冲叠加导致脉冲波峰偏移所引起的测距误差. εu来自于UDP状况,导致FDP不直视路径(DP, direct path)所产生的测距误差. UDP误差定义为
| $ {\varepsilon }_\text{u} = \left( {{t_{{\rm{FDP}}}} - {t_{\rm DP}}} \right)C $ | (2) |
其中:tFDP为FDP到达时间,tDP为DP理论到达时间.
根据上述分析,室内TOA测距误差可表示为
| $ {e_{{\rm{TOA}}}} = {\varepsilon} _\text{d} + {\varepsilon }_\text{m} + \delta \left( {{X_{{\rm{UDP}}}} - 1} \right){\varepsilon _{\rm{u}}} $ | (3) |
其中δ为冲击响应函数,定义如下:
| $ \delta \left( x \right) = \left\{ \begin{array}{l} 1,\;\;\;x = 0\\ 0,\;\;\;x \ne 0 \end{array} \right. $ | (4) |
当信道处于直视路径信号可测(DDP, detectable direct path)状况时,XUDP=0;当信道处于UDP状况时,XUDP=1.
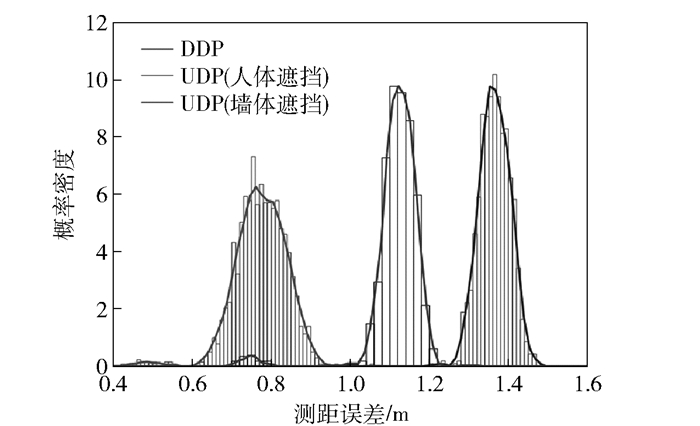
研究表明,DDP测距误差符合高斯分布;UDP测距误差通常比DDP误差大,而且由于遮挡物的不确定性,UDP测距误差的分布具有很大的不确定性. 图 2显示了通过DW1000射频芯片设计的UWB TOA测距节点测量的DDP误差分布,人体遮挡造成的UDP误差分布和墙体遮挡造成的UDP误差分布.从图 2可知,虽然3种测距误差都呈现高斯特征,但是由于三者同时存在而且各自所占的比例不可预测,测距误差总体上不符合零均值和同方差的假设.
|
图 2 DDP和UDP状态下的TOA测距误差分布 |
非线性规划是局部优化算法,因此初始值的设置对优化结果影响较大.首先利用最小二乘残差对原始测距值进行修正.将修正后的距离值作为非线性规划的初始值.
根据TOA测距结果,利用最小二乘法对定位目标节点位置进行初步估计.根据初步估计结果与基站位置坐标,可计算得到“计算距离”;根据“计算距离”与测距值,可得到“计算测距误差”.假设目标定位节点实际坐标为(x0, y0, z0),基站坐标为(xi, yi, zi), i=1, 2, …, n,可知
| $ d_i^2 = {\left( {{x_0} - {x_i}} \right)^2} + {\left( {{y_0} - {y_i}} \right)^2} + {\left( {{z_0} - {z_i}} \right)^2},\mathit{i} \text{= 1,2,} \cdots \mathit{,n} $ | (5) |
其中di为定位目标节点与第i个基站间实际距离;n为基站数.
| $ {d_i} = {{\hat d}_i} - {\varepsilon _i},i\text{ = }{\rm{1}}\mathit{,}{\rm{2}}\mathit{,} \cdots \mathit{,n} $ | (6) |
其中:
将式(6) 代入式(5),可得线性模型
| $ \mathit{\boldsymbol{AX = D + e}} $ | (7) |
其中,
| $ \mathit{\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} {\hat d_1^2 - \hat d_2^2 + x_2^2 - x_1^2 + y_2^2 - y_1^2 + z_2^2 - z_1^2}\\ {\hat d_1^2 - \hat d_3^2 + x_3^2 - x_1^2 + y_3^2 - y_1^2 + z_3^2 - z_1^2}\\ \vdots \\ {\hat d_1^2 - \hat d_n^2 + x_n^2 - x_1^2 + y_n^2 - y_1^2 + z_n^2 - z_1^2} \end{array}} \right] $ |
ei=(2d1ε1-2diεi+ε12-εi2),X=(x, y, z)′.利用最小二乘原理对式(7) 求解,使得‖e‖2最小,解得定位目标节点初步估计坐标为
| $ {\mathit{\boldsymbol{X}}^{\left( 0 \right)}} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{D}} $ |
计算X(0)与各定位基站的欧氏距离,结合TOA测距结果,可得到“计算测距误差”为
| $ {\varepsilon ^{\left( 1 \right)}} = \left( {\varepsilon _1^{\left( 1 \right)},\varepsilon _2^{\left( 1 \right)}, \cdots ,\varepsilon _n^{\left( 1 \right)}} \right) $ |
假设εm(1)=maxε(1),则优化后的测距值为
| $ {\mathit{\boldsymbol{d}}^{\left( 1 \right)}} = \left( {d_1^{\left( 1 \right)},d_2^{\left( 1 \right)}, \cdots ,d_n^{\left( 1 \right)}} \right),\left\{ \begin{array}{l} d_i^{\left( 1 \right)} = {{\hat d}_i} - \varepsilon _m^{\left( 1 \right)},i = m\\ d_i^{\left( 1 \right)} = {{\hat d}_i},i \ne m \end{array} \right. $ |
将d(1)作为非线性规划的初始值.
为了进一步对测距结果进行总体优化,最小化定位目标节点与基站间的测距误差,定义目标函数为
| $ \min J\left( \varepsilon \right) = \sum\limits_{i = 1}^n {\varepsilon _i^2} $ | (8) |
在三维定位中,需要获取定位目标节点与至少4个基站的测距信息.引入Cayley-Menger行列式及空间四面体几何约束作为求解式(8) 的约束条件.
2.2.1 Cayley-Menger行列式定义 在m维欧氏空间中,给定两组各有n个点组成的点列分别为{a1, a2, …, an}和{b1, b2, …, bn},则称矩阵
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{M}}\left( {{a_1},{a_2}, \cdots ,{a_n};{b_1},{b_2}, \cdots ,{b_n}} \right) \buildrel \Delta \over = }\\ {\left( {\begin{array}{*{20}{c}} {{d^2}\left( {{a_1},{b_1}} \right)}&{{d^2}\left( {{a_1},{b_2}} \right)}& \cdots &{{d^2}\left( {{a_1},{b_n}} \right)}&1\\ {{d^2}\left( {{a_2},{b_1}} \right)}&{{d^2}\left( {{a_2},{b_2}} \right)}& \cdots &{{d^2}\left( {{a_2},{b_n}} \right)}&1\\ \vdots & \vdots & \ddots & \vdots & \vdots \\ {{d^2}\left( {{a_n},{b_1}} \right)}&{{d^2}\left( {{a_n},{b_2}} \right)}& \cdots &{{d^2}\left( {{a_n},{b_n}} \right)}&1\\ 1&1& \cdots &1&0 \end{array}} \right)} \end{array} $ | (9) |
为两个点列的Cayley-Menger矩阵[12].其中,d(ai, bj)为点ai与bj之间的欧氏距离,i, j∈(1, 2, …, n).
定理 如果n≥m+2,则在m维空间中任意给定点列{a1, a2, …, an},都有
| $ \det \left[ {\mathit{\boldsymbol{M}}\left( {{a_1},{a_2}, \cdots ,{a_n};{a_1},{a_2}, \cdots ,{a_n}} \right)} \right] = 0 $ | (10) |
即该m维空间中n个点之间的距离并不是相互孤立的,而是满足式(10).因此,在三维空间中,当节点数目n≥5(至少4个基站)时,存在
| $ \begin{array}{l} \det \left[ {\mathit{\boldsymbol{M}}\left( {{p_1},{p_2}, \cdots ,{p_k},{p_0};{p_1},{p_2}, \cdots ,{p_k},{p_0}} \right)} \right] = 0\\ \buildrel \Delta \over = \left| {\begin{array}{*{20}{c}} 0& \cdots &{{d^2}\left( {{p_1},{p_k}} \right)}&{{d^2}\left( {{p_1},{p_0}} \right)}&1\\ \vdots & \ddots & \vdots & \vdots &1\\ {{d^2}\left( {{p_k},{p_1}} \right)}& \cdots &0&{{d^2}\left( {{p_k},{p_0}} \right)}&1\\ {{d^2}\left( {{p_0},{p_1}} \right)}& \cdots &{{d^2}\left( {{p_0},{p_k}} \right)}&0&1\\ 1& \cdots &1&1&0 \end{array}} \right| \end{array} $ | (11) |
其中:k≥4,p1, p2, …, pk为基站,p0为定位目标节点.
因此,在基于TOA测距的三维定位中,将式(6) 代入式(11),可得
| $ \begin{array}{l} G\left( \varepsilon \right) = \det \left[ {\mathit{\boldsymbol{M}}\left( {{p_1},{p_2},.\;.\;.,{p_k},{p_0};{p_1},{p_2},.\;.\;.,{p_k},{p_0}} \right)} \right]\\ \buildrel \Delta \over = \left| {\begin{array}{*{20}{c}} 0& \cdots &{{d_{1k}}}&{{{\left( {{{\hat d}_{10}} - {\varepsilon _{10}}} \right)}^2}}&1\\ \vdots & \ddots & \vdots & \vdots &1\\ {d_{k1}^2}& \cdots &0&{{{\left( {{{\hat d}_{k0}} - {\varepsilon _{k0}}} \right)}^2}}&1\\ {{{\left( {{{\hat d}_{01}} - {\varepsilon _{01}}} \right)}^2}}& \cdots &{{{\left( {{{\hat d}_{0k}} - {\varepsilon _{0k}}} \right)}^2}}&0&1\\ 1&1&1&1&0 \end{array}} \right|=0 \end{array} $ | (12) |
其中:dij(i, j≠0) 为基站间距,εij为对应基站与节点的测距误差.
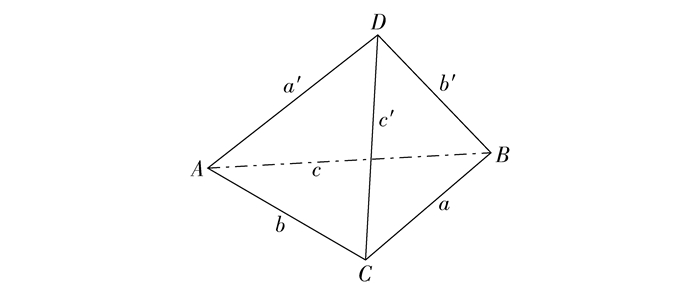
2.2.2 空间四面体定理定理 假设在三维空间中存在6条长度分别为a、a′、b、b′、c、c′的线段,那么这6条线段构成如图 3所示的四面体6条棱的重要条件[13]是
| $ \begin{array}{*{20}{c}} {F\left( {a,a',b,b',c,c'} \right) = }\\ {{a^2}{a^{'2}}\left( { - {a^2} - {a^{'2}} + {b^2} + {b^{'2}} + {c^2} + {c^{'2}}} \right) + }\\ {{b^2}{b^{'2}}\left( {{a^2} + {a^{'2}} - {b^2} - {b^{'2}} + {c^2} + {c^{'2}}} \right) + }\\ {{c^2}{c^{'2}}\left( {{a^2} + {a^{'2}} + {b^2} + {b^{'2}} - {c^2} - {c^{'2}}} \right) - }\\ {\left( {{a^2}{b^2}{c^2} + {a^2}{b^{'2}}{c^{'2}} + {a^{'2}}{b^2}{c^{'2}} + {a^{'2}}{b^{'2}}{c^2}} \right) > 0} \end{array} $ | (13) |
|
图 3 空间四面体 |
其中:长度分别为a与a′、b与b′、c与c′所对应的线段互为该四面体的一组对棱.
将四面体几何应用在三维定位系统中,则目标定位节点p0与任意3个定位基站可形成空间四面体,以1、2、3号基站(p1, p2, p3)为例,
| $ \begin{array}{*{20}{c}} {F\left( {{p_0},{p_1},{p_{2,}}{p_3}} \right) = }\\ {d_{13}^2d_{02}^2\left( { - d_{13}^2 - d_{02}^2 + d_{23}^2 + d_{01}^2 + d_{12}^2 + d_{03}^2} \right) + }\\ {d_{23}^2d_{01}^2\left( {d_{13}^2 + d_{02}^2 - d_{23}^2 - d_{01}^2 + d_{12}^2 + d_{03}^2} \right) + }\\ {d_{12}^2d_{03}^2\left( {d_{13}^2 + d_{02}^2 + d_{23}^2 + d_{01}^2 - d_{12}^2 - d_{03}^2} \right) - }\\ {\left( {d_{13}^2d_{23}^2d_{12}^2 + d_{13}^2d_{01}^2d_{03}^2 + d_{02}^2d_{23}^2d_{03}^2 + d_{02}^2d_{01}^2d_{12}^2} \right) > 0} \end{array} $ | (14) |
将式(6) 代入式(14),可以得到四面体约束条件为
| $ \begin{array}{*{20}{c}} {{F_1}\left( \varepsilon \right) = F\left( {{p_0},{p_1},{p_{2,}}{p_3}} \right) = }\\ {d_{13}^2{{\left( {{{\hat d}_{02}} - {\varepsilon _{02}}} \right)}^2}\left[ { - d_{13}^2 - {{\left( {{{\hat d}_{02}} - {\varepsilon _{02}}} \right)}^2} + } \right.}\\ {\left. {d_{23}^2 + {{\left( {{{\hat d}_{01}} - {\varepsilon _{01}}} \right)}^2} + d_{12}^2 + {{\left( {{{\hat d}_{03}} - {\varepsilon _{03}}} \right)}^2}} \right] + }\\ {d_{23}^2 + {{\left( {{{\hat d}_{01}} - {\varepsilon _{01}}} \right)}^2}\left[ {d_{13}^2 + {{\left( {{{\hat d}_{02}} - {\varepsilon _{02}}} \right)}^2} - d_{23}^2 - } \right.}\\ {\left. {{{\left( {{{\hat d}_{01}} - {\varepsilon _{01}}} \right)}^2} + d_{12}^2 + {{\left( {{{\hat d}_{03}} - {\varepsilon _{03}}} \right)}^2}} \right] + d_{12}^2\left( {{{\hat d}_{03}} - } \right.}\\ {{\varepsilon _{03}}^2\left[ {d_{13}^2 + {{\left( {{{\hat d}_{02}} - {\varepsilon _{02}}} \right)}^2} + d_{23}^2 + {{\left( {{{\hat d}_{01}} - {\varepsilon _{01}}} \right)}^2} - } \right.}\\ {\left. {d_{12}^2 - {{\left( {{{\hat d}_{03}} - {\varepsilon _{03}}} \right)}^2}} \right] - \left[ {d_{13}^2d_{23}^2d_{12}^2 + d_{13}^2\left( {{{\hat d}_{01}} - } \right.} \right.}\\ {{\varepsilon _{01}}^2{{\left( {{{\hat d}_{03}} - {\varepsilon _{03}}} \right)}^2} + {{\left( {{{\hat d}_{02}} - {\varepsilon _{02}}} \right)}^2}d_{23}^2\left( {{{\hat d}_{03}} - } \right.}\\ {\left. {{\varepsilon _{03}}^2 + {{\left( {{{\hat d}_{02}} - {\varepsilon _{02}}} \right)}^2}{{\left( {{{\hat d}_{01}} - {\varepsilon _{01}}} \right)}^2}d_{12}^2} \right] > 0} \end{array} $ | (15) |
同理,目标定位节点通过与不同的基站组合构成四面体,可得到各四面体约束条件Fk(ε),其中k=1, 2, …, Cn3,n为基站总数.
最终,建立带有约束条件的最优化问题
| $ \min J\left( \varepsilon \right) = \sum\limits_{i = 1}^n {\varepsilon _i^2}\\ {\rm{s}}{\rm{.}}\;{\rm{t}}{\rm{.}}\left\{ \begin{array}{l} G\left( \varepsilon \right) = 0\\ \mathit{F}\left( \varepsilon \right) > 0\\ \varepsilon > 0 \end{array} \right. $ | (16) |
利用迭代搜索方法求解式(16),并将ε(1)=(ε1(1), ε2(1), …, εn(1))设置为算法初始解,最终解得优化测距误差为ε(2)=(ε1(2), ε2(2), …, εn(2)).
2.2 定位根据测距误差优化结果,对TOA测距值进行优化得到优化测距值
| $ \mathit{\boldsymbol{AX = \bar D + e}} $ | (17) |
其中
| $ \mathit{\boldsymbol{\bar D}} = \left[ {\begin{array}{*{20}{c}} {\bar d_1^2 - \bar d_2^2 + x_2^2 - x_1^2 + y_2^2 - y_1^2 + z_2^2 - z_1^2}\\ {\bar d_1^2 - 2_3^2 + x_3^2 - x_1^2 + y_3^2 - y_1^2 + z_3^2 - z_1^2}\\ \vdots \\ {\bar d_1^2 - \bar d_n^2 + x_n^2 - x_1^2 + y_n^2 - y_1^2 + z_n^2 - z_1^2} \end{array}} \right] $ |
再次利用最小二乘法对式(17) 求解,解得定位目标节点最终估计位置
对算法进行实际场景下的测试,并对优化后的测距误差和定位精度与最小二乘算法和距离几何的定位算法(DGL, distance geometric location)[5]进行对比分析.
测试场景如图 4所示,在10 m×17 m的办公楼大厅中布置定位系统,使用基于DW1000射频芯片设计的UWB TOA测距节点,共采集1 549组测试数据,进行实际场景下的性能测试.在进行测试时,大厅中有正常的较为密集的人员走动.

|
图 4 实际测试场景 |
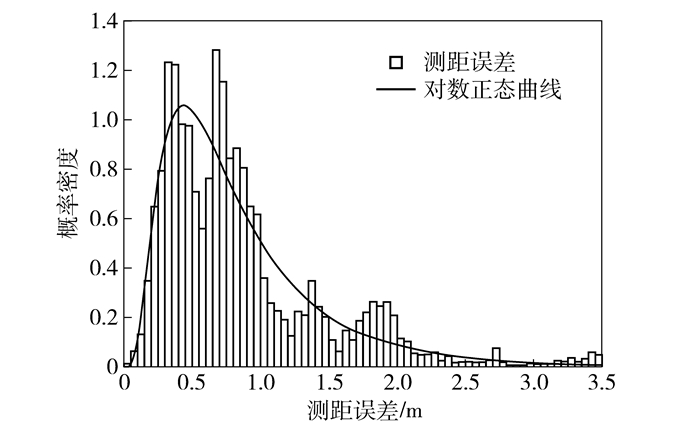
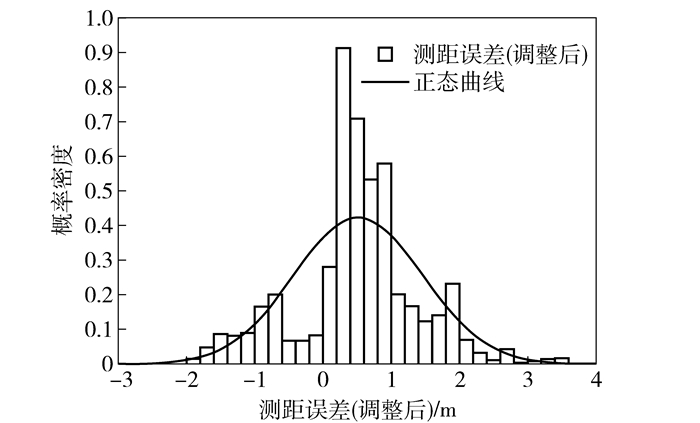
在测试环境中,存在着钢筋混凝土的墙体支柱以及一些金属的宣传牌和较为密集的人员走动.受到多径效应及遮挡的影响,测距误差呈现非高斯分布,如图 5所示.而且相对于正态分布而言,室内环境下的测距误差更多地呈现对数高斯分布.经过基于测距值优化的室内三维定位算法(DOLS, distance optimization based least square)对测距误差的优化后,测距误差的分布更加接近于零均值和同方差的分布特征,如图 6所示.此时使用最小二乘算法,可以取得较高的定位精度.
|
图 5 优化前的测距误差分布 |
|
图 6 优化后的测距误差分布 |
相比于平均绝对误差(MAE, mean absolute error),均方根误差(RMSE, root mean square error)对数据中异常点较敏感,更适合用于算法性能评估[14].这里使用定位误差的RMSE作为算法定位精度评估指标:
| $ {e_{{\rm{RMSE}}}} = \sqrt {E\left[ {\left( {\mathit{\boldsymbol{\hat X}} - {\mathit{\boldsymbol{X}}_0}} \right){{\left( {\mathit{\boldsymbol{\hat X}} - {\mathit{\boldsymbol{X}}_0}} \right)}^{\rm{T}}}} \right]} $ |
其中
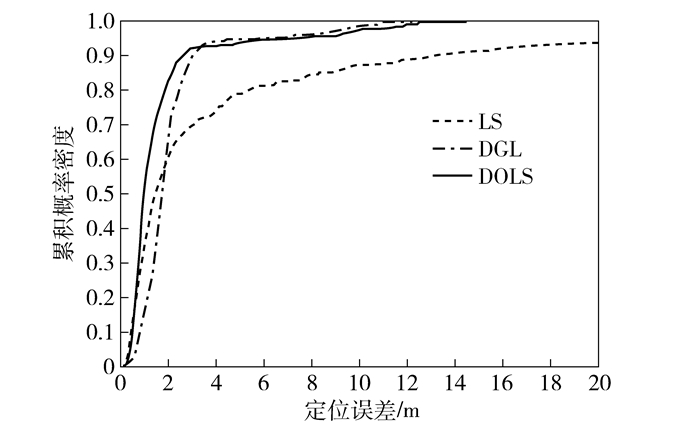
将笔者提出的DOLS算法与最小二乘算法和DGL算法进行定位精度比较,定位误差累积分布比较如图 7所示,各个算法的定位误差均值及其均方根误差如表 1所示.从图 7和表 1的对比结果可知,在实际场景的三维定位中,由于测距误差呈非高斯分布,最小二乘算法在实际应用中存在着误差很大的异常点,不适用于实际的应用. DOLS算法通过对测距误差进行调整使其更加接近零均值和同方差,然后利用最小二乘算法进行定位,在定位精度和稳定性方面均优于最小二乘算法和几何约束算法.
|
图 7 定位误差累计分布 |
|
|
表 1 定位误差均值及其均方根误差 |
在三维定位算法相关研究中,多数研究采用最小二乘法实现目标节点的三维定位.但由于传统最小二乘算法假设误差符合零均值和同方差的分布特征,而实际定位系统中TOA测距由于受到多径效应和非视距传输的影响,导致TOA测距结果具有非高斯特性,不满足上述假设.因此,直接利用最小二乘法的定位精度较差.
提出一种基于测距值优化的三维室内定位算法,结合残差修正、Cayley-Menger行列式及空间四面体理论,通过非线性规划方法,修正原始TOA测距值,使测距误差分布更接近与零均值和同方差的假设,提高算法定位精度.最后,通过在典型室内环境的定位实验,将DOLS算法与经典最小二乘算法、DGL算法进行对比.实验结果显示,DOLS算法具有较高的定位精度.
| [1] | Rantakokko J, Rydell J, Strömbäck P, et al. Accurate and reliable soldier and first responder indoor positioning:multisensor systems and cooperative localization[J]. IEEE Wireless Communications, 2011, 18(2): 10–18. doi: 10.1109/MWC.2011.5751291 |
| [2] |
王鹏, 张晓彤, 徐丽媛, 等. 基于自适应时延估计的室内近场测距算法[J]. 计算机学报, 2016, 39(32): 1–19.
Wang Peng, Zhang Xiaotong, Xu Liyuan, et al. Indoor near field ranging algorithm based on adaptive time delay estimation[J]. Chinese Journal of Computers, 2016, 39(32): 1–19. |
| [3] | Gandhi S R, Ganz A, Mullett G. FIREGUIDE:firefighter guide and tracker[C]//EMBC 2010. Buenos Aires:IEEE, 2010:2037-2040. |
| [4] | Ghidary S S, Nakata Y, Takamori T, et al. Localization and approaching to the human by mobile home robot[C]//RO-MAN 2000. Osaka:IEEE, 2000:63-68. |
| [5] | Li Zeyuan. Constrained weighted least squares location algorithm using received signal strength measurements[J]. China Communications, 2016, 13(4): 81–88. doi: 10.1109/CC.2016.7464125 |
| [6] | Akgul F O. Modeling the behavior of multipath components pertinent to indoor geolocation[M]. [S.l.]: Worcester Polytechnic Institute, 2010. |
| [7] | Bialer O, Raphaeli D, Weiss A J. Efficient time of arrival estimation algorithm achieving maximum likelihood performance in dense multipath[J]. IEEE Transactions on Signal Processing, 2012, 60(3): 1241–1252. doi: 10.1109/TSP.2011.2174055 |
| [8] | Erkmen B I, Moision B. Maximum likelihood time-of-arrival estimation of optical pulses via photon-counting photodetectors[C]//2009 IEEE International Symposium on Information Theory.[S.l.]:IEEE, 2009:1909-1913. |
| [9] | Liang S C, Liao L H, Lee Y C. Localization algorithm based on improved weighted centroid in wireless sensor networks[J]. Journal of Networks, 2014, 9(1): 183–189. |
| [10] | Chu Y, Ganz A. A UWB-based 3D location system for indoor environments[C]//2nd International Conference on Broadband Networks. Boston:IEEE, 2005:1147-1155. |
| [11] | Cao Ming, Anderson B D O, Morse A S. Sensor network localization with imprecise distances[J]. Systems & control letters, 2006, 55(11): 887–893. |
| [12] | Crippen G M, Havel T F. Distance geometry and molecular conformation[M]. Taunton: Research Studies Press, 1988. |
| [13] |
曾中君. 六正数构成四面体六棱长的充要条件.数学教学通讯[J]. 教师阅读, 2008(12): 38–39.
Zhongjun Zeng. A sufficient and necessary condition for six positive numbers to form six sides of a tetrahedron, mathematics teaching communication[J]. Teacher Reading, 2008(12): 38–39. |
| [14] | Chai T, Draxler R R. Root mean square error (RMSE) or mean absolute error (MAE)-arguments against avoiding RMSE in the literature[J]. Geoscientific Model Development, 2014, 7(3): 1247–1250. doi: 10.5194/gmd-7-1247-2014 |


