2. 清华大学 电子工程系, 北京 100084
针对盲干扰对齐机制平均功率分配导致功率利用率低的问题,提出了一种半盲干扰对齐功率分配算法.在功率受限场景下,该算法能够提高整体性能,同时保障个体性能.首先,分析了功率分配对盲干扰对齐性能的影响;其次,建立了功率受限的盲干扰对齐模型,提出了最大化传输速率同时保护用户个体性能的功率分配目标;最后,为满足目标函数的约束,提出基于回溯梯度下降的功率分配算法.仿真结果表明,相比于平均功率分配,所提算法可以将系统性提高约53%.
2. Department of Electronic Engineering, Tsinghua University, Beijing 100084, China
A power allocation algorithm was proposed to improve the power efficiency in semi-blind interference alignment. In the power-limited scenario, the proposed algorithm can improve the overall performance with individual performance guarantee. First, the impact of power allocation on the performance of blind interference alignment was analyzed. Second, the model of semi-blind interference alignment in the limited-power scenario is built and the optimal objective was proposed to maximize the transmission rate with individual performance guarantee. Finally, the retrospective gradient descent scheme based power allocation algorithm was designed and analyzed. Extensive simulations demonstrate that the performance of the proposed algorithm is about 53% higher than the average power allocation scheme.
盲干扰对齐[1]可以大幅提高多用户通信系统的自由度,已成为提高系统容量的有效手段.现有的盲干扰对齐机制[2]大都在发送功率无穷的场景下进行系统容量理论推导,只考虑简单的平均功率分配.实际场景中用户的信道状态不同,平均功率分配导致系统功率利用率较低,降低了系统传输速率[3].
为了解决上述问题,笔者分析了功率分配对盲干扰对齐性能的影响,建立了半盲干扰对齐功率分配优化目标,在功率受限的场景下优化系统传输速率,并在保证高速率用户性能的同时,提高低速率用户的性能.针对优化目标中的约束条件,提出基于用户对的梯度下降功率分配算法.
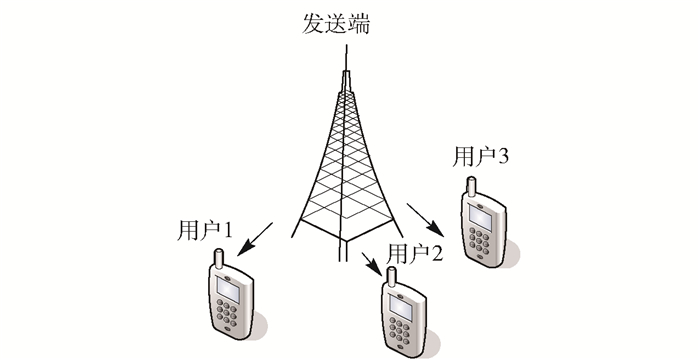
1 半盲干扰对齐功率分配模型 1.1 功率受限下的盲干扰对齐模型如图 1所示,以多输入单输出广播信道(MISO-BC, multiple-input single-output broadcast channel)为例,在传输过程中发送端没有信道状态信息,用户接收端可以获得完整的信道状态信息.发送端和不同用户间的信道是独立同分布的,且在传输过程中保持不变[1].发送端有M根天线,K个用户每人配备1根可重构天线,具有M个独立模式.用qk(t),qk(t)=1, 2, …, M表示用户k在时隙t的天线模式,用hk(·)(1×M的向量)表示用户k与发送端M根天线间的信道.在任意两个时隙t与t′中,当用户天线模式相同时,用户与发送端的信道状态相同,即qk(t)=qk(t′)时,hk(qk(t))=hk(qk(t′));当用户天线模式不同时,用户与发送端的信道状态独立,即qk(t)≠qk(t′)时,hk(qk(t))与hk(qk(t′))独立.
|
图 1 MISO BC盲干扰对齐模型 |
发送端发送给用户k的数据流(EDS, encoded data stream)为用户k的期望EDS,发送给其他用户j的EDS为用户k的干扰EDS.用xk=[xk1, xk2, …, xkM]H(M×1的向量)表示用户k的M个期望EDS.发送端在每个时隙中同时广播所有用户的期望EDS.用Pk(t)=E[‖xk‖2]表示时刻t分配给用户k每个期望EDS的功率,则用户k在时隙t的接收方程为
| $ \begin{array}{*{20}{c}} {{y_k}\left( t \right) = {\mathit{\boldsymbol{h}}_k}\left( {{q_k}\left( t \right)} \right)\left( {\sqrt {{P_k}\left( t \right)} {\mathit{\boldsymbol{x}}_k} + } \right.}\\ {\sum\limits_{j \ne k} {\left. {\sqrt {{P_j}\left( t \right)} {\mathit{\boldsymbol{x}}_j}} \right) + n\left( t \right)} } \end{array} $ | (1) |
其中,
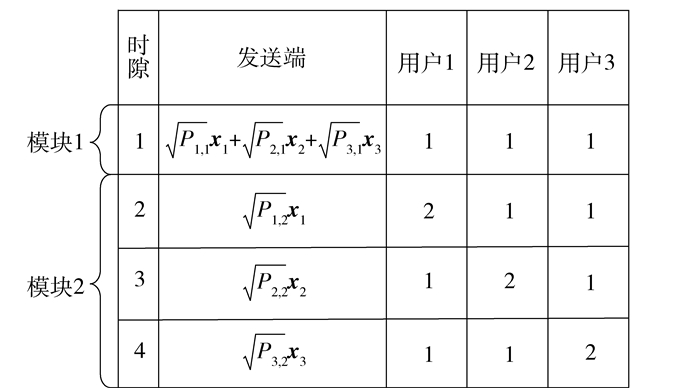
功率受限的盲干扰对齐的发送与接收机制如图 2所示.
|
图 2 功率受限场景下的盲干扰对齐发送机制与接收机制 |
以M=2,K=3为例.发送端首先发送所有用户EDS的和(这部分时隙称为模块1),然后单独发送每个用户的EDS(这部分时隙称为模块2).发送端在模块1内以Pk, 1的功率发送期望EDS给用户k,在模块2内以Pk, 2的功率发送期望EDS给用户k.发送功率满足
| $ \begin{array}{*{20}{c}} {{y_1}\left( 1 \right) = }\\ {{\mathit{\boldsymbol{h}}_1}\left( 1 \right)\left( {\sqrt {{P_{1,1}}} {\mathit{\boldsymbol{x}}_1} + \sqrt {{P_{2,1}}} {\mathit{\boldsymbol{x}}_2} + \sqrt {{P_{3,1}}} {\mathit{\boldsymbol{x}}_3}} \right) + n\left( 1 \right)} \end{array} $ | (2) |
| $ {y_1}\left( 2 \right) = {\mathit{\boldsymbol{h}}_1}\left( 2 \right)\sqrt {{P_{1,2}}\left( 2 \right)} {\mathit{\boldsymbol{x}}_1} + n\left( 2 \right) $ | (3) |
| $ {y_1}\left( 3 \right) = {\mathit{\boldsymbol{h}}_1}\left( 3 \right)\sqrt {{P_{2,2}}} {\mathit{\boldsymbol{x}}_2} + n\left( 3 \right) $ | (4) |
| $ {y_1}\left( 4 \right) = {\mathit{\boldsymbol{h}}_1}\left( 4 \right)\sqrt {{P_{3,2}}} {\mathit{\boldsymbol{x}}_3} + n\left( 4 \right) $ | (5) |
用户1的天线在第1、3、4个时隙均为模式1,用户1可以通过联合式(2)、式(4) 和式(5) 将用户1在式(1) 中接收到的其他用户的干扰EDS(x2,x3)消除.消除干扰后用户1的接收方程为
| $ \begin{array}{*{20}{c}} {{y_1}\left( 1 \right) - \sqrt {\frac{{{P_{1,1}}}}{{{P_{2,2}}}}} {y_1}\left( 3 \right) - \sqrt {\frac{{{P_{1,1}}}}{{{P_{3,2}}}}} {y_1}\left( 4 \right){\rm{ = }}}\\ {{\mathit{\boldsymbol{h}}_1}\left( 1 \right)\sqrt {{P_{1,1}}} {\mathit{\boldsymbol{x}}_1} + \mathit{n}\left( 1 \right) - \sqrt {\frac{{{P_{1,1}}}}{{{P_{2,2}}}}} n\left( 3 \right) - \sqrt {\frac{{{P_{1,1}}}}{{{P_{3,2}}}}} n\left( 4 \right)} \end{array} $ | (6) |
| $ {y_1}\left( 2 \right) = {\mathit{\boldsymbol{h}}_1}\left( 2 \right)\sqrt {{P_{1,2}}} {\mathit{\boldsymbol{x}}_1} + n\left( 2 \right) $ | (7) |
式(6) 与式(7) 中2个独立方程中含有2个未知量(x1=[x11, x12]H),用户1可以解码2个期望EDS.同理,用户2和用户3也可以解码其期望EDS.发送端在4个时隙中传输2×3个EDS.由于盲干扰对齐中1个EDS对应1个自由度,系统的自由度为
盲干扰对齐机制会使噪声在用户端叠加.式(6) 中噪声功率增加至式(2) 中的
为了反映盲干扰对齐机制带来的噪声叠加,将用户直接接收到的信噪比称为接收信噪比(rSNR, received signal-noise-ratio),将用户在模块1中消去干扰后的信噪比(在盲干扰对齐机制中,模块2时隙中的噪声没有叠加,因此只考虑模块1中的fSNR)称为最终信噪比(fSNR, final signal noise ratio).根据式(1),用户k的fSNR为
| $ {\mathit{\gamma }_k} = \frac{{{P_k}}}{{{P_z}}}E\left[ {{{\left\| {{\mathit{\boldsymbol{h}}_k}\left( {{q_k}\left( t \right)} \right)} \right\|}^2}} \right] $ | (8) |
其中Pk为信号功率.由于n(t)~CN(0, 1),Pz=1为噪声功率.由于用户天线不同模式对应的信道独立同分布[1],设αk=E[‖hk(qk(t))‖2],则
| $ {\mathit{\gamma }_k} = {P_k}{\alpha _k} $ | (9) |
用户k的fSNR为
| $ {\mathit{\Gamma }_k} = \frac{{{\mathit{\boldsymbol{\gamma }}_k}}}{{1 + \sum\limits_{j \ne k} {\frac{{{P_{k,1}}}}{{{P_{j,2}}}}} }} = 1 + \frac{{{P_{k,1}}{\alpha _k}}}{{\sum\limits_{j \ne k} {\frac{{{P_{k,1}}}}{{{P_{j,2}}}}} }} $ | (10) |
根据文献[6]中Theorem 2,当采用平均分配发送功率时,盲干扰对齐中用户k的可达传输速率为
| $ {R_k} = \frac{1}{{M + K - 1}}E\left[ {{\rm{lbdet}}\left( {{\mathit{\boldsymbol{I}}_M} + \frac{{{\mathit{\boldsymbol{H}}_k}\mathit{\boldsymbol{H}}_k^\text{H}}}{{{\alpha _k}}}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_k}} \right)} \right] $ | (11) |
其中IM为M×M的单位矩阵,Hk=[hk(1), …, hk(M-1), hk(M)],
| $ {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_k} = \left[ {\begin{array}{*{20}{c}} {\frac{{\frac{P}{{MK}}{\alpha _k}}}{{1 + \frac{{K - 1}}{K}}}{\mathit{\boldsymbol{I}}_{M - 1}}}&\boldsymbol{0}\\ \boldsymbol{0}&{\frac{\mathit{P}}{M}{\alpha _k}} \end{array}} \right] $ | (12) |
其中Γk为M×M对角矩阵,对角线上每个元素代表对应方程中的fSNR.
在功率受限的实际场景中,由式(11) 可知系统容量由用户的fSNR和信道状态决定.尽管盲干扰对齐技术可以达到自由度的上限,但由于盲干扰对齐中用户fSNR的降低及用户间信道的差异,当采用平均功率分配时,系统的实际传输速率不一定随着自由度的增加而上升.因此,不同于盲干扰对齐中优化自由度的目标,在进行功率分配时,选择以最大化系统总速率为优化目标.
1.2 半盲干扰对齐功率分配模型将用户的传输速率按照其fSNR分为N+1档,其中第n+1档表示用户的fSNR介于γth, n-1~γth, n,其对应的传输速率为rk, n,如表 1所示.根据式(10) 和表 1,在功率分配调整的过程中,用户只需在初始化阶段反馈1次信道的统计特征值αk,之后发送端可以直接查表得到功率调整后对应的传输速率,无需用户端进行多次反馈.
|
|
表 1 用户k传输速率与fSNR的对应关系 |
具体而言,半盲干扰对齐功率分配算法处理过程如下.
步骤1 发送端首先发送导频给用户.
步骤2 用户根据导频进行信道估计.
步骤3 用户k向发送端反馈自己的信道统计值γk, ∀k.
步骤4 发送端根据用户反馈的信道统计值进行半盲干扰对齐功率分配算法.
在传统的盲干扰对齐机制中,仍需要执行步骤1和步骤2的信道估计过程[1],从而使用户获取信道状态信息.在半盲干扰对齐功率分配算法中,用户端需要的额外开销仅需要在步骤3中向发送端反馈信道统计值,占用带宽较小.同时,半盲干扰对齐功率分配算法在发送端实现,不会造成用户端计算复杂度的增加.
以传输速率作为衡量实际场景中评价盲干扰对齐的指标,则功率受限的传输速率最大化问题可以描述为
| $ \mathop {\max }\limits_{{P_{k,1}},{P_{k,2}},\forall k} \sum\limits_k {{r_k}} $ | (13) |
满足
单纯优化目标函数式(13) 虽然能够保证提高系统整体性能,但不能保证每个用户的个体性能,即优化该目标函数可能牺牲一部分用户的个体性能.用户选择加入盲干扰对齐机制中协作进行干扰消除,盲干扰对齐机制的功率分配应该保护用户的个体性能,同时兼顾整体性能的优化.
为了在保证个体性能的同时协同优化整体性能,选取表 1中的一个传输速率门限γth, n,1≤n≤N,将用户分为两类(γth, n可根据实际信道情况选取).在平均功率分配的机制下,用户k的fSNR称为初始fSNR,表示为Γkori.如果Γkori≥γth, n,则用户k为高速率用户,反之则用户k为低速率用户.为了在保证高速率用户的性能的前提下优化低速率用户的性能,功率分配的算法应尽量提高低速率用户的传输速率,同时保证高速率用户的传输速率仍在γth, n以上.上述约束可表示为
| $ {\mathit{\Gamma }_k} \ge {\mathit{\gamma }_{{\rm{th,}}\mathit{n}}},\mathit{\Gamma }_k^{{\rm{ori}}} \ge {\mathit{\gamma }_{{\rm{th,}}\mathit{n}}}\\ {\mathit{\Gamma }_k} \ge \mathit{\Gamma }_k^{{\rm{ori}}},\mathit{\Gamma }_k^{{\rm{ori}}} < {\mathit{\gamma }_{{\rm{th,}}\mathit{n}}} $ | (14) |
综上,半盲干扰对齐中的功率分配优化目标函数可表示为
| $ \mathop {\max }\limits_{{P_{k,1}}{P_{k,2}},\forall k} Q = \sum\limits_k {{r_k}}\\ {\rm{s}}{\rm{.t}}{\rm{.}}{\mathit{\Gamma }_k} \ge {\gamma _{{\rm{th,}}\mathit{n}}},\mathit{\Gamma }_k^{{\rm{ori}}} \ge {\gamma _{{\rm{th,}}\mathit{n}}}\\ \;\;\mathit{\Gamma }_k \ge \mathit{\Gamma }_k^{{\rm{ori}}},\mathit{\Gamma }_k^{{\rm{ori}}} < {\gamma _{{\rm{th,}}\mathit{n}}}\\ \;\;\;\sum\limits_k {{P_{k,1}} = P}\\ \;\;\;{P_{k,2}} = P,\forall k $ | (15) |
通过发送端调整不同用户期望EDS的发送功率,提高系统的总传输速率,同时兼顾用户个体的传输速率.梯度下降法能够以平均功率分配的结果作为初始解,不断寻找满足约束条件且目标函数增长最快的方向,快速迭代收敛到局部最优解.然而,典型的梯度下降方法在第一次寻找到的局部最优解后停止搜索,无法在更大的可行解空间范围内搜索其他局部最优解.为此,提出一种基于回溯的梯度下降算法,通过回溯梯度下降过程,搜索更多的可行解的分支,增强寻找性能更好的局部最优解的概率.具体步骤如下.
步骤1 初始化.令A0(t)={P1, 1(t), P2, 1(t), …, Pk, 1(t), …, PK, 1(t)}表示第t次迭代时模块1中的功率分配.其中Pk, 1(t)为发送端在第t次迭代向用户k发送期望EDS的功率.在初始状态(t=1),发送端缺少用户反馈的信道状态统计信息,每个时隙中所有EDS的功率相同,即A0(1)={P1, 1(1), P2, 1(1), …, Pk, 1(1), …, PK, 1(1)},
步骤2 生成当前解A0(t)的可行邻居解的集合F(A0(t)).首先,发送端基于每个用户反馈的信道统计特征值γk、∀k和式(10),得到每个用户的fSNRk, ∀k, 并根据式(14) 确定每个用户为高速率用户或低速率用户.
在总发送功率一定的约束下
步骤3 梯度下降搜索局部最优解.基于表 1,选择F(A0(t))中目标函数Q的增量最大的功率分配方式作为下一个当前解.重复该步骤直至在第T0次迭代目标函数Q不再变化,则算法找到一个局部最优解A0(T0).
步骤4 回溯梯度下降过程.设回溯过程包括N轮,不失一般性,考虑第i, i=1, 2, …, N轮回溯过程.
1) 获得第i-1轮的每个局部最优解的梯度下降过程.假设第i-1轮回溯过程包括Si-1个局部最优解,针对第s个局部最优解,其梯度下降的过程可以表示为:
| $ \underbrace {{\mathit{A}_{i - 1,s}}\left( 1 \right) \to {A_{i - 1,\mathit{s}}}\left( 2 \right) \to \cdots {\mathit{A}_{i - 1,s}}\left( t \right) \to {\mathit{A}_{i - 1,s}}\left( {Ti - 1,s - 1} \right) \to {\mathit{A}_{i - 1,s}}\left( {Ti - 1,s} \right)}_{Ti - 1,s{\rm{次迭代}}} $ |
当i=1时,只回溯局部最优解A0(T0)(S0=1) 的梯度下降过程:
| $ \underbrace {{A_0}\left( 1 \right) \to {A_0}\left( 2 \right) \to \cdots {A_0}\left( t \right) \to {A_0}\left( {{T_0} - 1} \right)\to {A_0}\left( {{T_0}} \right)}_{{T_0}{\rm{次迭代}}} $ |
2) 针对第i-1轮的任意一个梯度下降过程经过的点Ai-1, s(t), i=1, 2, …, N; s=1, 2, …, Si-1; t=1, 2, …, Ti-1, s,在其可行邻居解F(Ai-1, s(t))中随机选择一个解作为初始解,重复步骤2和步骤3,得到以Ai-1, s(t)作为初始点的局部最优解,并将该局部最优解作为第i轮的一个局部最优解.
步骤5 在N轮回溯得到的所有局部最优解集合中选择目标函数Q最大的局部最优解作为功率分配方式,算法结束.
随着回溯轮数N的增加,回溯的梯度下降算法计算复杂度非线性增加.同时,回溯轮数的增加更有利于算法性能的提升.在实际中,应在计算复杂度的约束下选择最大的回溯轮数.其次,由于功率分配算法在发送端进行,其用户只需要在第一次迭代中反馈信道的统计特征值,不需要用户随着迭代次数的增加反馈更多的信道信息.
2.2 系统可达传输速率根据式(10),当发送端在模块1内以Pk, 1的功率发送期望EDS给用户k,在模块2内以Pk, 2的功率发送期望EDS给用户k时,用户k在M个方程中的fSNR为
| $ {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_k}{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {\frac{{{P_{k,1}}{\alpha _k}}}{{1 + \sum\limits_{j \ne k} {\frac{{{P_{k,1}}}}{{{P_{j,2}}}}} }}{\mathit{\boldsymbol{I}}_{M - 1}}}&{\bf{0}}\\ {\bf{0}}&{{P_{k,2}}{\alpha _k}} \end{array}} \right] $ | (16) |
根据式(11),用户k的可达传输速率为
| $ {R_k} = \frac{1}{{M + K - 1}}E\left[ {{\rm{lbdet}}\left( {{\mathit{\boldsymbol{I}}_M} + \frac{{{\mathit{\boldsymbol{H}}_k}\mathit{\boldsymbol{H}}_k^{\rm{H}}}}{{{\alpha _k}}}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_k}} \right)} \right] $ | (17) |
其中Hk=[hk(1), …, hk(M-1), hk(M)].则该系统的系统可达传输速率为
| $ R = \sum\limits_k {{R_k}} $ | (18) |
在仿真场景中,M=3,K=15个用户随机分布在距发送端半径为20 m的圆形区域内. P=-10 dBm,噪声功率为-104 dBm.发送端与用户k间信道的路径损耗公式为PL(dk)=32.5+20lgdk,小尺度衰落服从CN(0, 1).区分用户高低速率的SNR门限选为γth, 3=15 dB.根据实际信道选定Γk与所对应的速率如表 2所示. ΔP=-30 dBm.回溯梯度算法中N=10.每个仿真场景重复200次以统计数据分布.
|
|
表 2 仿真场景中用户k传输速率与fSNR的对应关系 |
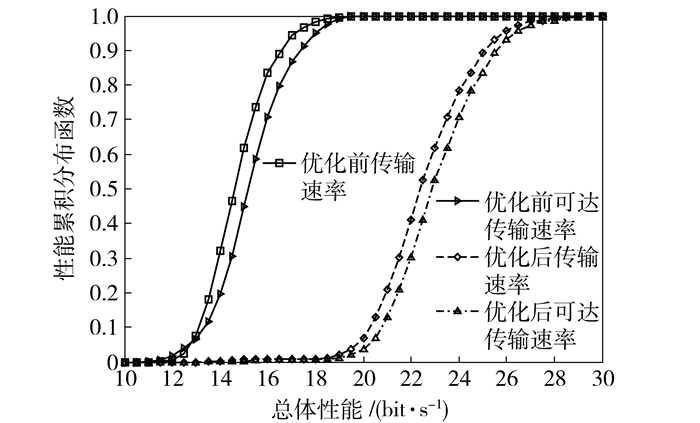
系统优化前和优化后的总体性能累积分布函数(CDF, cumulative distribution function)如图 3所示.系统优化前可达传输速率的80%分位数约为16 bit/s,优化后约为24.5 bit/s.由于所提算法可以搜索到性能较好的局部最优解,系统性能提高约53%.同时,优化过程中根据用户fSNR档位估计传输速率,优化后的传输速率更接近于可达传输速率.
|
图 3 总体性能CDF |
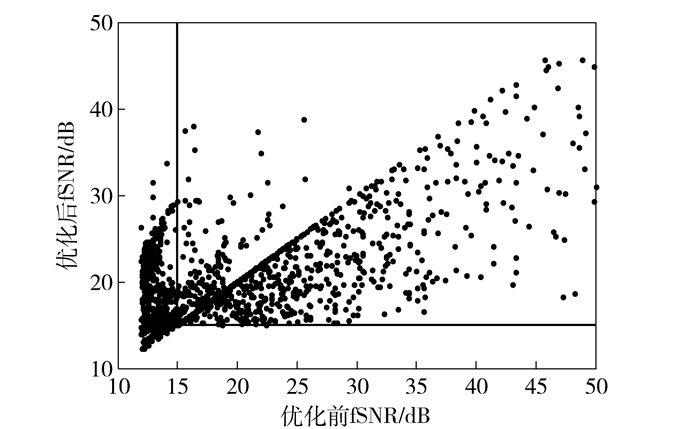
图 4给出了每个用户优化前后fSNR的对比.由图 4可以看出,原本的低速率用户(原始fSNR小于15 dB)性能有所提高,高速率用户(原始fSNR大于15 dB)性能下降以提高整体性能,但仍保持在15 dB以上,即在保证高速率用户性能的基础上提高低速率用户性能,满足优化目标中的约束.
|
图 4 个体性能 |
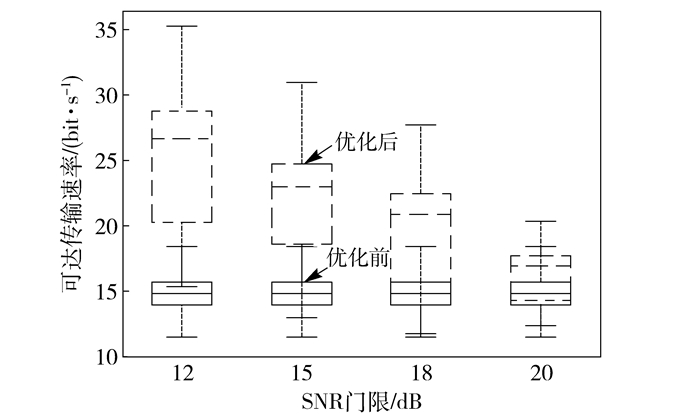
图 5描述了SNR门限对可达传输速率的影响.实线箱式图和虚线箱式图分别表示优化前和优化后的性能.优化前系统性能不受SNR门限的影响,其性能不变.优化后性能随SNR门限增高而降低.这是由于当SNR门限较低时,所有用户都为高速率用户,其功率可以在很大范围内调节均满足约束.当SNR门限较高时,大部分的用户为低速率用户,其优化后的性能只能增加不能减少.功率可调节范围很小,导致性能提升变小.
|
图 5 SNR门限对可达传输速率的影响 |
分析了功率受限场景下功率分配对盲干扰对齐性能的影响,建立了半盲干扰对齐功率分配模型.提出了基于回溯梯度下降法的半盲干扰对齐功率分配算法.该算法提高了系统的整体性能,同时在保证高速率用户性能的前提下提高低速率用户的性能.仿真表明,功率分配优化后的可达传输速率较平均功率分配的可达传输速率提高约53%.
| [1] | Gou Tiangao, Wang Chenwei, Jafar S A. Aiming perfectly in the dark-blind interference alignment through staggered antenna switching[J]. IEEE Transactions on Signal Process, 2011, 59(6): 2734–2744. doi: 10.1109/TSP.2011.2129517 |
| [2] |
章扬, 周正, 石磊, 等. 基于严格势博弈的干扰对齐[J]. 北京邮电大学学报, 2013, 36(2): 50–54.
Zhang Yang, Zhou Zheng, Shi Lei, et al. Interference alignment based on exact potential game[J]. Journal of Beijing University of Posts and Telecommunications, 2013, 36(2): 50–54. |
| [3] | Wang Chenwei, Papadopoulos H C, Ramprashad S A, et al. Improved blind interference alignment in a cellular environment using power allocation and cell-based clusters[C]//ICC 2011. Kyoto:IEEE, 2011:5-9. |
| [4] | Yang Qing, Jiang Ting, Jiang Chunxiao, et al. Joint optimization of user grouping and transmitter connection on multi-cell SNR blind interference alignment[J]. IEEE Access, 2016, 54: 4974–4988. |


