大多数用户相似性算法在计算用户相似性时只考虑了用户间的共同评分项,而忽略了用户其他评分中可能隐藏的有价值信息.为了准确评估用户间的相似性,提出了一种基于KL散度的用户相似性协同过滤算法.该算法不仅利用了共同评分项,还考虑了其他非共同评分信息的影响.该算法充分利用了用户的所有评分信息,提高了用户相似性度量的可靠性和准确性.实验结果表明,该算法优于当前主流的用户相似性算法,且在没有共同评分信息的条件下,仍能有效地完成用户相似性度量,解决了对共同评分项的完全依赖问题,具有更好的适应性.
User similarity based collaborative filtering algorithm is one of most widely used technologies. Most of user similarity algorithms only consider the co-rated items between two users, but ignore other ratings that probably hide valuable information. To evaluate user similarity accurately, a user similarity collaborative filtering algorithm based on Kullback-Leibles (KL) divergence was proposed. The proposed algorithm utilizes both the co-rated items and the influence of other no co-rated items. Since the algorithm makes full use of all rating information, it improves the accuracy and reliability of user similarity. Experiments show that the proposed algorithm outperforms other user similarities. Moreover, it can still measure the user similarity effectively, even if no co-rated items exist. Therefore, the presented algorithm solves the problem of full dependence on co-rated items and gains better flexibility.
协同过滤算法利用用户已有的偏好去预测未来对某产品的偏好,以满足用户的个性化需求.数据稀疏性问题是该领域的常见问题之一,为解决此问题,许多相似性度量方法被提出[1~3].然而,这些算法普遍存在的问题是,只使用了共同评分信息,忽略了其他非共同评分信息的影响.笔者借助KL(Kullback-Leibles)散度提出了一种新的用户相似性协同过滤算法.该算法既能有效处理共同评分项中的信息,还能充分利用其他的非共同评分项信息,具有更好的客观性与全面性,且能有效地应对数据集稀疏的问题,具有很好的应用价值.
1 预备知识协同过滤推荐算法通常是利用已有的评分数据来预测用户对未评价项目的偏好程度.已有的评分数据可表示为表 1所示的User-Item评分矩阵,其中用户集合为U={u1, u2, …, um},项目计划为I={i1, i2, …, in},ruj为用户u对项目j的评分.
|
|
表 1 User-Item评分矩阵 |
值得注意的是,User-Item评分矩阵通常是一个非常稀疏的矩阵.如何设计相似性计算方法以解决评分矩阵的稀疏性问题,是该领域的研究热点之一.
1.1 用户相似性模型用户相似性计算是协同过滤推荐算法中极其重要的部分,对推荐结果有至关重要的影响.常见的具有代表性的用户相似性计算模型包括修正余弦相似性(ACOS,adjusted cosine similarity)、皮尔逊相关系数(PC,Pearson correlation coefficient)和约束皮尔逊相关系数(CPC,constrained Pearson’s correlation)等,对应的计算式如下[1].
ACOS:

|
(1) |
PC:
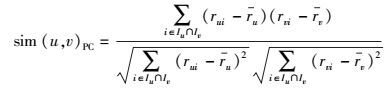
|
(2) |
CPC:
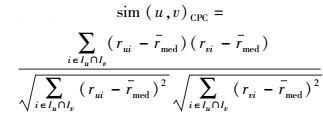
|
(3) |
其中:Iu为用户u已评分的项目集合,ru为用户u对所有已评项目的评分均值,rmed为评分区间中值.
上述用户相似性方法在计算过程中只考虑了用户的共同评分项,而忽略了非共同评分的价值.当共同评分项少或不存在时,这些方法将会出现较大的偏差或不可用,从而影响最后的推荐效果.
1.2 最近邻居集最近邻居集Nu是针对目标用户u,计算用户u与其他用户间的相似性值,然后按照相似性值从大到小的筛选规则,选取出前n个用户.这n个用户组成的集合就是用户u的最近邻居集.
1.3 评分预测规则根据用户u的最近邻居集合Nu,可得用户u对未评分项目i的预测评分pui,其计算式为[1]

|
(4) |
传统方法在计算2用户间相似性时,通常只考虑了2用户的共同评分项.在实际应用中,由于数据集的稀疏性会导致共同评分项十分稀少,从而造成用户间相似性测量的误差偏大,影响推荐效果.笔者希望在计算用户相似性时能充分利用2个用户的所有评分信息,而不只是共同评分项.为此,提出如下的用户相似性计算模型.
设用户u,v对项目i,j的评分分别为(rui, -)和(-, rvj).由于用户间没有共同评分,采用1.1节中的公式无法计算用户u和v的相似性.这样的情况在评分矩阵中广泛存在.如果能利用非共同评分计算出用户的相似性,将极大地提升用户相似性计算式的应用范围.通常用户u和v会对多个项目进行评分,因而在计算用户相似性时应综合考虑所有评分组合.为此,引入的计算公式为

|
(5) |
其中:Iu为用户u的所有评分项集合;ru和σu分别为用户u的平均评分和标准差.设s=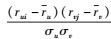

|
(6) |
由式(6) 知,当s值较大,且项目i和j相似,则sim(i, j)items值较大,计算的结果是增强用户u和v的相似性;相反,当s值较大,且项目i和j不相似时,则sim(i, j)item的值较小,导致sim(i, j)items的值也较小,从而削弱用户u和v的相似性.当s值较小时,可得类似的结果.式(6) 是所有可能的评分对的加权和,是一个累积的统计结果,不容易受局部评分的影响,因此具有更好的客观性和全面性.
此外,由式(6) 可知,sim(i, j)item对计算结果有重要影响.在设计sim(i, j)item的计算式时希望能满足如下要求:1) 不受共同评分项的限制,具有良好的适应性;2) 可利用所有的评分信息,具有良好的全面性.笔者采用基于KL散度的项目相似性来计算sim(i, j)item,可满足上述要求.
2.2 基于KL散度的项目相似性1) KL散度
KL散度又称KL距离,从概率分布的角度去衡量2个变量间的距离[4~5].假设ρ1和ρ2分别为2个不同的概率密度函数,对于离散数据集D,KL距离定义为[4]

|
(7) |
其中ρ1(x)>0和ρ2(x)>0.
2) 项目相似性计算
基于上述定义,在Uses-Item评分矩阵中,对任意2项目i和j,将所有用户对它们的评分视作2个变量序列,可得项目i与j的KL距离D(i, j)的计算式为[2]

|
(8) |
其中:ρi为项目i的密度函数,rmax为评分区间的最大值;ρir
根据KL距离,可得基于KL的全局项目相似性计算公式为[2]
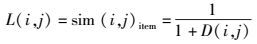
|
(9) |
由于KL距离不具有对称性,而度量2项目间的距离时需要具有对称性,笔者采用式(10) 代替式(9) 中的D(i, j).
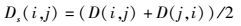
|
(10) |
将式(6) 中的项目相似性sim(i, j)item替换为式(9),可得最终的基于KL散度的用户相似性计算公式为
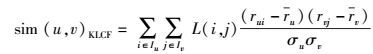
|
(11) |
利用2.1~2.3节中用户相似性计算的关键步骤和1.3节中的评分预测规则,得到基于KL散度的用户相似性协同过滤算法(KLCF,Kullback-Leibles collaborative filtering)如下.
输入:Uses-Item评分矩阵.
输出:用户u对未评分项目的预测评分值.
① 利用式(8) 和式(10) 得到项目i和j的KL距离Ds(i, j);
② 利用式(9) 计算项目i和j的KL相似性L(i, j);
③ 重复步骤①②,计算所有项目间的相似性;
④ 利用式(11) 计算用户u和其他用户间的相似性,并筛选出前n个相似性值最高的用户作为用户u的最近邻居集合;
⑤ 利用式(4) 得到最终的预测评分值.
3 算法分析1) 充分利用所有评分信息
传统的相似性度量方法,如余弦相似性等,是完全依赖于共同评分项的.若用户间不存在共同评分项,则这类方法将无法进行相似性计算.在稀疏数据集中,用户通常只对万千项目中的一小部分评分,所以用户间的共同评分项极度稀少.例如MovieLens数据集中,2用户间的共同评分数量平均仅占他们总评分数量的4%.若仅依靠共同评分项,则可利用的信息很少,容易造成较大的误差.笔者的方法同时利用了共同评分信息和其他的非共同评分信息,解决了上述不足,且使算法具有更好的适应性.由于笔者方法更充分的利用了所有评分项信息,因此提高了计算的准确性.
2) 充分利用了KL散度优势
式(11) 中项目相似性是基于KL散度设计的.将评分矩阵中2个项目的所有评分视作2条序列时,由于评分范围有限(常为5级或10级),所以2条序列之间必然存在大量重叠点. KL散度是利用评分值的概率分布去度量项目间的相似程度.已有研究[5]表明,KL散度的优势在于它能高效区分欧式距离难以区别的对象,尤其是当2个数据集中的数据出现大量重叠时,优势更为明显.基于KL散度的项目相似性从统计角度使用了所有的评分信息,结果不容易受特殊情况影响,具有更好的客观性.此外,该方法对用户所评项目的数量没有要求,即使在极为稀疏的数据集中也能很好的测量项目的相似性,具有很好的适应性.
3) 利用绝对评分值区别不同用户
Jaccard系数相似性方法[1]虽然也利用了用户的所有评分值,但它只考虑了共同评分项目的比例,而忽略了绝对评分值对计算结果的影响.这导致Jaccard方法难以区分不同的用户,该结论在文献[1]中已有验证.笔者的方法同时考虑了用户评分绝对值和它在项目所有评分中的比例,所以可有效克服Jaccard方法存在的不足,更好地区分用户.
4 实验结果与分析4.1 数据集采用公开数据集MovieLens①中最新公布的ML-Lastest-Small和Yahoo Music②作为笔者算法测试和验证的数据集.各数据集的描述如表 2所示,其中稀疏度
② http://research.yahoo.com/Academic_Relations
|
|
表 2 实验数据集相关信息描述 |
为测试算法,将每个数据集划分为2部分,随机筛选出的80%数据作为训练集,余下的20%作为测试集.
4.2 评价指标预测准确性是衡量协同过滤算法性能的一个重要参考标准,常用平均绝对误差(MAE,mean absolute error)来进行度量,计算式为

|
(12) |
其中:m为目标用户的个数,n为用户u预测的项目数;rui和pui分别为用户u对项目i的实际评分值和预测评分值.
推荐准确性是衡量推荐算法性能的另一重要参考标准,常用准确率P、召回率C和F1值来进行评估,对应计算式为[6]

|
(13) |
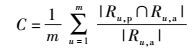
|
(14) |

|
(15) |
其中Ru, p和Ru, a分别为预测推荐的项目集合和真实推荐的项目集合. F1值为P和C的综合评价指标,F1值越大,推荐效果越好.
4.3 结果分析为了与笔者方法进行对比,在相同的数据集中,对协同过滤方法皮尔森相关系数(PCC,Pearson correlation coefficient)[1],约束的皮尔森相关系数(CPCC,constrained Pearson correlation coefficient)[1],平均平方差(MSD,mean squared difference)[3],接近-影响-普及(PIP,proximity-impact-popularity)[1],新的启发式相似性模型(NHSM,new heuristic similarity model)[1]和Bhattacharyya系数协同过滤(BCF,Bhattacharyya coefficient in collaborative filtering)[3]进行了测试.最终得到的实验结果如图 1、图 2所示.
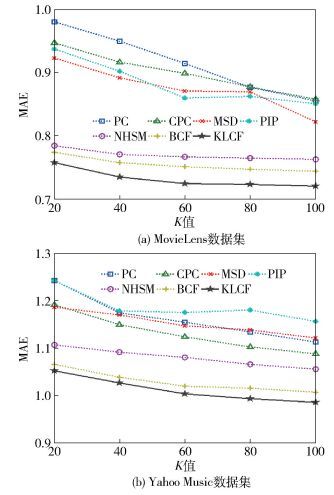
|
图 1 MAE测试结果 |

|
图 2 F1值结果比较 |
MAE反映的是预测评分值与用户实际评分值之间的平均差异程度. 图 1(a)中,笔者提出KLCF算法的MAE值总体范围为0.718≤E≤0.745,对于最接近的BCF算法,精确度提高了约2%;图 1(b)中,当K值为100时,KLCF的MAE值最小,为0.986. 图 1整体反映出KLCF算法的MAE值最小,具有良好的预测精度,且明显优于其他算法.
4.3.2 F1值比较在此处的实验中,将预测值大于用户平均评分的项目作为推荐项目,并以此为基础计算F1值. 图 2(a)中,KLCF算法的F1值比BCF算法提高了6.6%;图 2(b)中,当K值大于40时,只有KLCF的F1值超过0.6. 图 2中的结果表明,KLCF算法在2个数据集上均有良好的推荐效果,且优于其他算法.
5 结束语为解决用户相似性计算依赖于共同评分项的问题,提出了一种基于KL散度的用户相似性协同过滤算法.该算法同时利用了共同评分信息和非共同评分信息,克服了已有方法受制于共同评分项的限制,对稀疏数据集具有更好的适应性.在计算项目相似性时,基于KL散度从所有评分信息的概率分布角度进行测量,由于充分利用了所有的信息,故增强了算法的可靠性和准确性.数据实验及其对比的结果表明,该算法具有良好的性能,且优于已有的常用协同过滤算法,具有很好的应用潜力.
| [1] | Liu Haifeng, Hu Zheng, Mian Ahmad, et al. A new user similarity model to improve the accuracy of collaborative filtering[J].Knowledge Based Systems, 2014, 56(11): 156–166. |
| [2] |
王永, 邓江洲, 邓永恒, 等. 基于项目概率分布的协同过滤推荐算法[J]. 现代图书情报技术, 2016, 32(6): 73–79.
Wang Yong, Deng Jiangzhou, Deng Yongheng, et al. A collaborative filtering recommendation algorithm based on item probability distribution[J].New Technology of Library and Information Service, 2016, 32(6): 73–79. doi: 10.11925/infotech.1003-3513.2016.06.09 |
| [3] | Patra B K, Launonen R, Ollikainen V, et al. A new similarity measure using Bhattacharyya coefficient for collaborative filtering in sparse data[J].Knowledge-Based Systems, 2015, 82(3): 163–177. |
| [4] | Kullback S, Leibler R A. On information and sufficiency[J].The Annals of Mathematical Statistics, 1951(22): 79–86. |
| [5] | Huang Anna. Similarity measures for text document clustering[C]//the New Zealand Computer Science Research Student Conference(NZCSRSC). New Zealand:[s.n.], 2008:49-56. |
| [6] | Zhang Jing, Peng Qinke, Sun Shiquan, et al. Collaborative filtering recommendation algorithm based on uses preference derived from item domain features[J].Physica A, 2014, 396(2): 66–76. |




