采用带精英策略的非支配排序遗传算法(NSGA-Ⅱ)对通信电缆的绞合节距进行优化,以通信电缆的导体用量和近端串音衰减为优化目标,获得一组多样化的Pareto解集,为绞合节距的设计提供了优选空间.以25线对通信电缆的绞合节距为优化对象,结果表明,经优化获得157个Pareto解,其目标函数导体用量位于区间[55.93 kg/km,56.74 kg/km],近端串音衰减位于区间[58.11 dB/km,94.77 dB/km];与粒子群算法(PSO)相比,在收敛时长相似的情况下,NSGA-Ⅱ的优化结果支配度100%优于PSO,其解集分布均匀程度也显著优于PSO.
Lay length of communication cable was optimized using non-dominated sorting genetic algorithm-Ⅱ (NSGA-Ⅱ). Two object functions of communication cable dosage and near-end cross talk attenuation were designed. The solutions over diversified Pareto front were obtained. Lay length of communication cable with 25 pairs was studied as the optimization object. It is shown that 157 solutions are obtained and the dosage is in the range of[55.93 kg/km, 56.74 kg/km], the near-end cross talk attenuation is in the range of[58.11 dB/km, 94.77 dB/km]. The superiority of NSGA-Ⅱ is verified compared with particle swarm optimization. The convergence time of NSGA-Ⅱ and PSO are similar, the solutions of NSGA-Ⅱ are 100% better than PSO and distribute more evenly.
随着信息时代的到来,信息传输量呈爆炸式增长.作为信息传输的载体,通信电缆的需求量不断提高.通信电缆是指用于近距音频通信和远距高频载波数字通信及信号传输的电缆,是中国的五大电缆产品之一.绞合节距是指单线沿轴线旋转一周所前进的距离.在传输各种通信信号的过程中,近端串音干扰是影响通信电缆通信质量的重要因素之一[1].在同一根通信电缆中,通过合理选择各线对的绞合节距可以降低线对间的串音影响,然而,绞合节距的变化又直接影响到通信电缆的导体用量,即通信电缆的制造成本.因此,研究同时满足近端串音和导体用量要求的绞合节距优化方法具有重要的意义.
为降低近端串音干扰对通信电缆通信质量的影响,国内外已有关于绞合节距设计的标准.国内,如行业标准YD/T 322—2013和国家标准GB/T 13849.1—2013;国外,如美国标准ANSI/ICEA S-84-608-2002和ANSI/ICEA S-85-625-2002.其中,国内行业标准YD/T 322—2013和国家标准GB/T 13849.1—2013均指出对于长度大于3 m的线对,其平均绞合节距最大不应超过150 mm.
目前,绞合节距的选取没有明确的计算公式,国家标准GB/T 3956—2008给出了节距比的设计范围,在节距比设计范围内对绞合节距进行设计,但未考虑绞合节距对导体用量的影响.笔者根据绞合节距对近端串音干扰和导体用量的影响,提出了一种基于带精英策略的非支配排序遗传算法(NSGA-Ⅱ, non-dominated sorting genetic algorithm-Ⅱ)的通信电缆绞合节距优化方法.该方法以通信电缆的导体用量和近端串音衰减为优化目标,设计了优化目标函数,并采用NSGA-Ⅱ获取绞合节距Pareto解集,为通信电缆绞合节距的设计提供了优选空间.
1 优化模型以25线对通信电缆的绞合节距为优化对象,25线对做3+9+13三层绞合,通信电缆的排列方式如图 1所示,图中数字为线对编号[2].通信电缆的长度L=1 km,线芯(铜芯)的直径d=0.4 mm,线对中心到导线中心的距离ρd=0.35 mm.

|
图 1 25线对排列方式 |
作为绞合工艺的主要参数,绞合节距的确定既要考虑其对通信质量(近端串音衰减)的影响,同时也要考虑其对生产成本(导体用量)的影响.因此,绞合节距的优化属于多目标优化问题,即

|
(1) |
其中:FW为目标函数导体用量;FN为目标函数近端串音衰减;hi为线对i的绞合节距,绞合节距最大值150 mm依据国家标准GB/T 13849.1—2013给出.
2 NSGA-Ⅱ非支配排序遗传算法(NSGA, non-dominated sorting genetic algorithm)由Srinivas等于20世纪90年代提出,主要用于求解多目标优化问题. Deb等[3]于2002年在NSGA的基础上进行了改进,提出了NSGA-Ⅱ,解决了NSGA的高计算复杂度以及多样性保持等问题.
2.1 优化目标函数1) 导体用量
导体用量,即在通信电缆制造过程中,线芯导体的使用量.绞合节距越小,绞入系数越高,导体用量越大,即绞合节距与导体用量成反比.导体用量φW和绞入系数λ的计算公式分别为
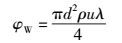
|
(2) |

|
(3) |
其中:d为单根导体直径,ρ为导体密度,u为导体绞合根数,D=1.71d为绞合外径.
2) 近端串音衰减
近端串音的计算通常使用近端串音衰减进行量化,近端串音衰减值越大则线对间的近端串音干扰越小.本研究中,由于通信电缆中有25线对,相应的有C252组线对间的近端串音衰减,取其最小值为目标函数.近端串音衰减的计算公式为
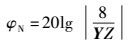
|
(4) |
其中:Z为线对的特性阻抗,Y为近端串音耦合矢量.近端串音耦合矢量的计算公式为

|
(5) |

|
其中:ε=ε0εr,ε0为真空介电常数,εr为通信电缆的相对介电常数;μ=μ0μr,μ0为真空磁导率,μr为通信电缆的相对磁导率;η(0<η<1) 为主被串线对间存在的其他导线屏蔽作用所需的修正系数;r0为导线半径;γ为主被串线对的传播常数;x为沿通信电缆轴端的距离;L1(x)和L2(x)为线芯间距离函数.
由式(5) 可以看出,近端串音耦合主要与L1(x)和L2(x)相关,且L1(x)和L2(x)是x的函数,呈周期性变化.通信电缆中线对及其镜像的位置如图 2所示. L1(x)和L2(x)的计算公式分别为

|
图 2 通信电缆中线对及其镜像位置 |
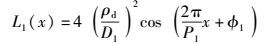
|
(6) |

|
(7) |
其中:φ1、φ2为不含x的常数,其数值可忽略;D1为线对a的中心与线对b的中心之间的距离;D2为线对a的镜像中心与线对b的中心之间的距离;R为通信电缆半径;a,b为电缆内任意两线对;P1、P2分别为L1(x)和L2(x)的空间波动周期,P1、P2的计算公式为

|
(8) |
研究所设计的优化目标函数包括导体用量FW和近端串音衰减FN,属于多目标优化问题,通过采用非支配排序方法可以获得一组Pareto解集,该解集各解向量具有非劣性,即对于解集中任意一个解向量Hj1,在该解集中不存在解向量Hj2可同时满足:① FW(Hj2)≤FW(Hj1)且FN(Hj2)≥FN(Hj1);② FW(Hj2)<FW(Hj1)或FN(Hj2)>FN(Hj1)[6~8].
2.3 NSGA-Ⅱ优化过程采用NSGA-Ⅱ对通信电缆绞合节距进行优化前,首先确定计算所需的各项参数.相对介电常数εr=1.62 F/km,相对磁导率μr=1 H/km,则
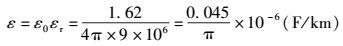
|
(9) |
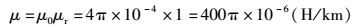
|
(10) |
计算导体用量FW时,导体密度取8.9 g/cm3;计算近端串音衰减FN时,选取近端耦合频率fN=1 024 kHz,这时阻抗Z≈110 Ω,修正系数η取1.
根据国家标准GB/T 13849.1—2013,确定绞合节距的优化范围(≤150 mm),设定近端串音衰减的最小值(≥58 dB/km).
完整的NSGA-Ⅱ步骤如下.
步骤1 设置种群规模Np=800,初始迭代次数t=0,最大迭代次数Tmax=10 000.
步骤2 随机产生规模为Np的初始解集Ht=[Ht, 1, …, Ht, j, …, Ht, Np]T,其中Ht, j=[h1t, j, …, hit, j, …, h25t, j],t=0,(t为迭代次数,i为绞合线对编号,j为当前解集中解的编号).
步骤3 计算每次迭代过程中的目标函数导体用量FW和近端串音衰减FN.
步骤4 按非支配排序规则对解集Ht排序,确定Ht所有非劣层(F1t, F2t, …, Fnt).
步骤5 在Ht中随机选择2个个体,比较其非劣层号和拥挤距离,选择较好的一个放入父代种群Pt,Pt规模为Np/2.
步骤6 进行交叉和变异操作产生子代解集Qt,Qt规模为Np.
步骤7 合并Pt和Qt,Mt=Pt∪Qt.
步骤8 按非支配排序规则对解集Mt排序,确定Mt所有非劣层(F1t, F2t, …, Fnt).
步骤9 计算Fkt(k=1, 2, …, n)拥挤距离,执行Ht+1=Ht+1∪Fkt,直到|Ht+1|+|Fkt|≤|Ht|,并从Fk+1t中选取拥挤距离最大的(|Ht|-|Ht+1|)个解加入Ht+1.
步骤10 判断是否满足终止条件(t=Tmax),若满足,则输出F1t(Pareto解集);若不满足,则t=t+1,转步骤3.
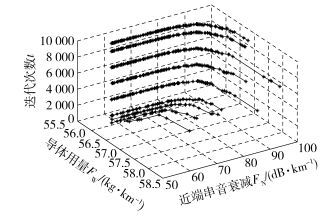
3 NSGA-Ⅱ优化结果通过NSGA-Ⅱ对通信电缆绞合节距进行优化,并获得了其迭代过程及Pareto解集,如图 3所示.
|
图 3 NSGA-Ⅱ迭代过程 |
图 3中由下到上分别为NSGA-Ⅱ第1、100、500、1 000、3 000、5 000、7 000、9 000和10 000次迭代中获得的Pareto解集,X、Y轴分别为目标函数FW、FN,Z轴为迭代次数.结果表明如下:
1) 随着迭代次数增加,NSGA-Ⅱ算法逐渐趋于收敛,FW呈减小趋势,FN呈增大趋势,与目标函数优化方向一致;
2) 算法运行至1万代时,迭代终止. Pareto解集的FW最终稳定在区间[55.93 kg/km,56.74 kg/km],FN稳定在区间[58.11 dB/km,94.77 dB/km];
3) 随着迭代次数增加,Pareto解集个数逐渐增加,NSGA-Ⅱ解集个数由8增至157,且在区间内的分布越来越均匀.
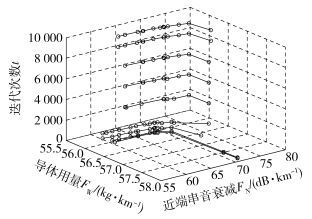
4 NSGA-Ⅱ优化性能分析为验证NSGA-Ⅱ优化性能,将NSGA-Ⅱ与粒子群算法(PSO, particle swarm optimization)进行了对比研究[9~10]. PSO的基本参数设置:学习因子c1=2、c2=1,惯性权重wt+1=wt×0.99、w0=0.5,其他相应参数与NSGA-Ⅱ一致. PSO的迭代过程如图 4所示.
|
图 4 PSO迭代过程 |
从图 4中可以看出,PSO的运行结果与NSGA-Ⅱ相比,总体趋势是一致的.随着迭代次数增加,Pareto解集个数逐渐增加,由7增至13,且最终FW稳定在区间[55.97 kg/km,56.62 kg/km],FN稳定在区间[61.95 dB/km,75.67 dB/km].
对NSGA-Ⅱ和PSO结果进行比较分析,主要包括:① Pareto解集之间的支配关系,即解的优劣;② Pareto解集分布的均匀程度;③ Pareto解集的收敛时长.
4.1 Pareto解集的支配关系不同解集之间的支配关系是评价解集优劣的重要标准,首先采用2种算法分别获得了Pareto解集,如图 5所示.其次,对2个解集进行非支配排序,并通过分析第一非劣层中,NSGA-Ⅱ和PSO解集所占的比例(PNSGA-Ⅱ和PPSO),实现2个解集整体的优劣程度的判断,对比结果表明,NSGA-Ⅱ和PSO的占比分别为PNSGA-Ⅱ=100%和PPSO=0,显然,采用NSGA-Ⅱ算法获得的解集显著优于PSO.

|
图 5 NSGA-Ⅱ和PSO优化结果 |
Pareto解集分布的均匀程度表征了解集的多样性(非劣解的选择空间).采用平均距离s对Pareto解集的均匀程度进行评价,计算公式为

|
(11) |
其中:φ为目标函数FW或FN,v为Pareto解集的规模.平均距离s越短,表明Pareto解集分布越均匀.结果表明:① 以FW进行评价,NSGA-Ⅱ和PSO的分布均匀程度分别为0.008 2和0.054 1;② 以FN进行评价,NSGA-Ⅱ和PSO的分布均匀程度分别为0.239 0和1.143 2. NSGA-Ⅱ的Pareto解集分布更均匀.
4.3 Pareto解集的收敛时长NSGA-Ⅱ和PSO运行10 000代的时长分别为29 560 s和29 008 s,2种算法的收敛时长相差不大,PSO略占优.
5 结束语针对通信电缆绞合节距的优化问题,研究设计了近端串音衰减FW和导体用量FN 2个目标函数,并采用NSGA-Ⅱ对其进行优化.优化结果表明:
1) 采用NSGA-Ⅱ优化方法可以得到一组有效的Pareto解集,该解集的FW最终稳定在区间[55.93 kg/km,56.74 kg/km],FN稳定在区间[58.11 dB/km,94.77 dB/km],且在区间内分布均匀,为通信电缆绞合节距的选取提供了优选空间.
2) 随着迭代次数增加,NSGA-Ⅱ的Pareto解集个数由8增至157,且逐渐收敛,说明采用该方法求解通信电缆绞合节距问题是有效可行的.
3) 通过与PSO的优化结果进行对比,结果表明2种算法在收敛时长相似的情况下,NSGA-Ⅱ的优化结果支配度100%优于PSO;以FW和FN进行解集分布均匀程度评价,NSGA-Ⅱ均占优.
| [1] |
高瑶, 李有明, 洪顺利, 等. 用户下线时抑制串音的自更新算法[J]. 电子学报, 2012, 40(7): 1368–1371.
Gao Yao, Li Youming, Hong Shunli, et al. Crosstalk cancellation self-updating algorithm in changing interference environment when old users getting offline[J].Acta Electronica Sinica, 2012, 40(7): 1368–1371. |
| [2] |
杨黎明, 朱智恩, 杨荣凯, 等. 柔性直流电缆绝缘料及电缆结构设计[J]. 电力系统自动化, 2013, 37(15): 117–124.
Yang Liming, Zhu Zhien, Yang Rongkai, et al. Insulation material and structure design of HVDC flexible cables[J].Automation of Electric Power Systems, 2013, 37(15): 117–124. doi: 10.7500/AEPS20130607005 |
| [3] | Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm:NSGA-Ⅱ[J].IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182–197. doi: 10.1109/4235.996017 |
| [4] | |
| [5] |
肖飚. 关于对绞型通信电缆串音问题的探讨[J]. 电线电缆, 2007, 2(2): 6–12.
Xiao Biao. On the crosstalk of the pair-twisted telecom cables[J].Electric Wire & Cable, 2007, 2(2): 6–12. |
| [6] |
王茜, 张粒子. 采用NSGA-Ⅱ混合智能算法的风电场多目标电网规划[J]. 中国电机工程学报, 2011, 31(19): 17–24.
Wang Qian, Zhang Lizi. Multi-objective transmission planning associated with wind farms applying NSGA-Ⅱ hybrid intelligent algorithm[J].Proceedings of the CSEE, 2011, 31(19): 17–24. |
| [7] | Li Peng, Wang Yuhua, Hu Jingru, et al. Sensors distribution optimization for impact localization using NSGA-Ⅱ[J].Sensor Review, 2015, 35(4): 409–418. doi: 10.1108/SR-02-2015-0028 |
| [8] |
盛万兴, 叶学顺, 刘科研, 等. 基于NSGA-Ⅱ算法的分布式电源与微电网分组优化配置[J]. 中国电机工程学报, 2015, 35(018): 4655–4662.
Sheng Wanxing, Ye Xueshun, Liu Keyan, et al. Optimal allocation between distributed generations and microgrid based on NSGA-Ⅱ algorithm[J].Proceedings of the CSEE, 2015, 35(018): 4655–4662. |
| [9] |
石文孝, 范绍帅, 王楠, 等. 基于PSO模糊神经元的异构无线网络接入选择[J]. 北京邮电大学学报, 2011, 34(2): 58–62.
Shi Wenxiao, Fan Shaoshuai, Wang Nan, et al. A PSO-fuzzy neuron based access selection in heterogeneous wireless networks[J].Journal of Beijing University of Posts and Telecommunications, 2011, 34(2): 58–62. |
| [10] |
王晶, 陈骏宇, 蓝恺. 基于实时电价的微网PSO最优潮流算法研究[J]. 电力系统保护与控制, 2013, 41(16): 34–40.
Wang Jing, Chen Junyu, Lan Kai. PSO optimal power flow algorithm for a microgrid based on spot power prices[J].Power System Protection and Control, 2013, 41(16): 34–40. doi: 10.7667/j.issn.1674-3415.2013.16.005 |


