2. 广东工业大学 信息工程学院, 广东 510075
在经典Jerk混沌系统和现有多涡卷混沌系统最新研究成果的基础上,引入符号函数构建了一个能够产生立体网格多涡卷混沌吸引子的新型混沌系统模型.该模型的动力学分析和Matlab数值仿真结果表明,该系统能够产生立体网格2×2×2多涡卷混沌吸引子.最后,设计了硬件电路,并且给出了立体网格2×2×2多涡卷的硬件电路实验结果.硬件实验结果与理论分析、仿真结果一致,从而验证了该系统的物理可实现性.
2. School of Information Engineering, Guangdong University of Technology, Guangdong 510075, China
Based on the classical Jerk chaotic system and the latest research of multi-scroll chaotic system, a model of the new chaotic system was constructed to produce 3-D grid multi-scroll chaotic attractors with the sign function in the modified Jerk's circuit. Both model analysis and Matlab simulation show that the system generates 3-D 2×2×2-grid multi-scroll chaotic attractors. Finally, the design of the hardware circuit was made at 3-D 2×2×2-grid multi-scroll hardware experiments. Hardware experiments. Analysis and simulation are full matched that is proven the physical realization of the system.
20世纪70年代,美国气象专家Lorenz提出了著名的Lorenz系统,并揭示了混沌运动的基本特征,为混沌应用奠定了基础[1]. 2000年,Sprott提出了三阶Jerk系统[2~4],引起了国内外混沌研究者的关注.研究表明,利用低维简单混沌加密的系统可以被破译,而性态复杂的高维多涡卷混沌系统难以被破译,因此围绕多涡卷混沌系统的研究成为一个热点.
2007年以来,Yalcin、Suykens和Vandewalle研究小组提出了使用分段线性函数等产生多涡卷混沌吸引子的方法,并且给出了最多6涡卷混沌吸引子的电路实验结果[5~7].近年来,学者们提出利用分段线性函数、阶梯波函数、符号函数、正弦波函数、时滞函数、三角波函数、锯齿波函数等多种方法产生多涡卷混沌吸引子[8~14].从现有文献报道来看,多涡卷混沌吸引子的研究主要集中在单向多涡卷,关于网格多涡卷混沌系统的研究较少,并且从实际硬件电路中产生网格多涡卷的混沌吸引子并非易事.
1 立体网格2×2×2多涡卷混沌系统1.1 经典Jerk混沌系统经典Jerk混沌系统的表示形式为
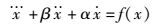
|
(1) |
其中: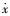
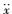
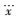
Jerk系统是一类满足Poincare-Bendixson定理[15]的数学形式非常简单的三阶自治混沌系统. Jerk混沌系统的特点是数学方程形式简洁,便于电路实现,可以通过时间尺度变换所需的频谱范围,广泛应用于保密通信领域.
1.2 系统构造笔者在经典Jerk混沌系统的基础上,引入符号函数作为非线性函数,同时对经典Jerk混沌电路中的参数进行修正,构造了立体网格2×2×2多涡卷混沌系统的无量纲状态方程:

|
(2) |
其中:a=1.4,b=1.4,c=1.5,d=0.8,e=3.9,非线性函数f1、f2、f3为
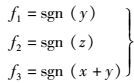
|
(3) |
提出的系统做(x, y, z)→(-x, -y, -z)变换后,保持不变,即系统关于原点对称,且这种对称性对所有的参数均成立.
1.3.2 系统散度提出的系统是一个耗散系统,其散度∇V为
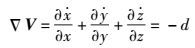
|
(4) |
提出系统的收敛速率为
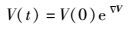
|
(5) |
因为d>0,所以提出的系统是耗散的,当t→∞时,包含系统轨线的每一个体积元都以指数率-d的速度收缩,体积元即系统的外微分形式,初始体积元V(0) 的体积元在时间t时收缩为体积元V(0) e-d,即一个吸引子上.
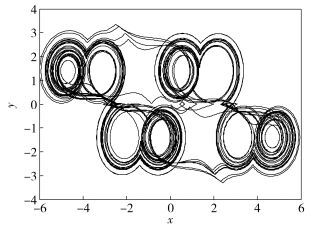
2 系统仿真分析对式(2) 所示系统采用龙格-库塔法积分,初始值(x, y, z)=(0.01, -0.01, -0.01),系统混沌吸引子的Matlab仿真结果如图 1所示.
|
图 1 立体网格2×2×2多涡卷混沌吸引子的Matlab仿真结果 |
由图 1可以看出,该系统产生了立体网格2×2×2多涡卷混沌吸引子.与单向多涡卷混沌系统相比,立体网格多涡卷混沌系统相轨在更多方向上分离,具有更为复杂的非线性动力学行为,可以抵御常规破译方法.
3 硬件电路设计与实现根据模块化电路设计思想,对式(2) 进行微分-积分变换,得到
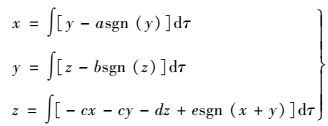
|
(6) |
其中:a=1.4,b=1.4,c=1.5,d=0.8,e=3.9.根据式(6),设计出如图 2所示电路. 图 2中的运算放大器型号为TL082,所有有源器件的电源电压均为±15 V,所有电阻均采用精密可调电阻或精密可调电位器.

|
图 2 硬件电路 |
对图 2所示电路进行硬件实验可得如图 3所示的实验结果,该实验结果是通过数码相机从模拟示波器上获得的.

|
图 3 硬件电路实验结果 |
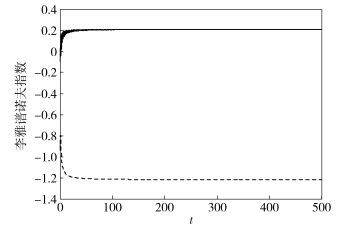
对式(2) 所示系统采用龙格-库塔法积分,时间t=(0, 600),初始值(x, y, z)=(0.01, -0.01, -0.01),系统李雅谱诺夫指数谱的Matlab仿真结果如图 4所示.
|
图 4 系统李雅谱诺夫指数谱 |
由图 4可以看出,系统李雅谱诺夫指数l1=0.209 816,l2=0.208 915,l3=-1.218 731.混沌系统统计特性由轨道拉伸折叠变换决定,一个正李雅谱诺夫指数的混沌系统有一个方向的拉伸折叠变换和发散度,而所提出的混沌系统有多个正李雅谱诺夫指数,所以该系统具有多个不同方向的拉伸折叠变换.
Garcia-Martinez等[12]提出的混沌系统能够产生10涡卷混沌吸引子,系统正李雅谱诺夫指数分别为0.136 181和0.135 918.正李雅谱诺夫指数越大,系统的运动越复杂,因为所提出的混沌系统正李雅谱诺夫指数均大于Garcia-Martinez等提出的混沌系统,所以提出的混沌系统混沌化程度更高,混沌序列统计特性更好,更利于提高混沌保密通信和混沌信息加密的安全性,具有更重要的理论意义和实际应用价值.
5 结束语基于经典Jerk混沌系统,使用符号函数作为非线性函数构建了一个能够产生立体网格多涡卷混沌吸引子的新型混沌系统模型.给出了Matlab数值仿真结果,并设计了硬件电路和进行了相应的硬件实验.硬件实验结果与理论分析和仿真结果完全吻合,证实了该系统不仅是一个立体网格多涡卷混沌系统,而且是物理可实现的系统.值得注意的是,笔者给出了立体网格2×2×2多涡卷的硬件电路实验结果,该实验结果是目前不可多得的实验成果.随着多涡卷混沌理论在科学和工程技术领域中的应用研究不断深入,以多涡卷混沌理论为基础的保密通信将逐渐取代低维混沌加密机制而日趋完善.
| [1] | Lorenz E N. Deterministic nonperiodic flow[J].Journal of the Atmospheric Sciences, 1963, 20(2): 130–141. doi: 10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2 |
| [2] | Sprott J C. Simple chaotic systems and circuits[J].American Journal of Physics, 2000, 68(8): 758–763. doi: 10.1119/1.19538 |
| [3] | Sprott J C. A new class of chaotic circuit[J].Physics Letters A, 2000, 266(1): 19–23. doi: 10.1016/S0375-9601(00)00026-8 |
| [4] | Shaik K B, Mandal M K. Chaos from Jerk circuit[J].National Institute of Technology, 2010: 257–267. |
| [5] | Yalcin M E. Multi-scroll and hypercube attractors from a general Jerk circuit using josephson junctions[J].Chaos Solitons & Fractals, 2007, 34(5): 1659–1666. |
| [6] | Kilinc S, Yalcin M E, Ozoguz S. Multiscroll chaotic attractors from a hysteresis based time-delay differential equation[J].International Journal of Bifurcation and Chaos, 2010, 20(10): 3275–3281. doi: 10.1142/S0218127410027660 |
| [7] | Yeniceri Ramazan, Yalcin M E. Multi-scroll chaotic attractors from a generalized time-delay sampled-data system[J].International Journal of Circuit Theory and Applications, 2016, 44(6): 1263–1276. doi: 10.1002/cta.v44.6 |
| [8] | Henry Alombah N, Hilaire Fotsin, Megam Ngouonkadi E B, et al. Dynamics, analysis and implementation of a multiscroll memristor-based chaotic circuit[J].International Journal of Bifurcation and Chaos, 2016, 26(8): 16501281–20. |
| [9] | He Shaobo, Sun Kehui, Wang Huihai. Modified multiscale permutation entropy algorithm and its application for multiscroll Ccaotic systems[J].Complexity, 2016, 21(5): 52–58. doi: 10.1002/cplx.v21.5 |
| [10] | Sajad Jafari, Viet-Thanh Pham, Tomasz Kapitaniak. Multiscroll chaotic sea obtained from a simple 3D system without equilibrium[J].International Journal of Bifurcation and Chaos, 2016, 26(2): 1–7. |
| [11] | Wu Xianming, He Yigang. A systematic design method for 3D grid multiscroll chaotic attractors and its circuit implementation employing CFOAs[J].International Journal of Bifurcation and Chaos, 2015, 25(3): 1–10. |
| [12] | Garcia-Martinez M, Ontanon-Garcia L J, Campos-Canton E, et al. Hyperchaotic encryption based on multi-scroll piecewise linear systems[J].Applied Mathematics and Computation, 2015(270): 413–424. |
| [13] | Hu Xiaoyu, Liu Chongxin, Liu Ling, et al. Multi-scroll hidden attractors in improved sprott a system[J].Nonlinear Dynamics, 2016, 86(3): 1725–1734. doi: 10.1007/s11071-016-2989-5 |
| [14] | Yuan Fang, Wang Guangyi, Wang Xiaowei. Extreme multistability in a memristor-based multi-scroll hyper-chaotic system[J].Chaos, 2016, 26(7): 1–10. |
| [15] | Sprott J C, Linz S J. Algebraically simple chaotic flows[J].Chaos Theory and Applications, 2000(5): 3–20. |


