提出两种事件约束的时间不确定事件流查询处理方法.基于可能世界的查询处理方法,根据事件约束的不确定事件查询语义,通过对可能世界的遍历获取查询结果.基于事件约束优先的查询处理方法中,根据事件约束计算其所涉及事件发生时间的联合分布律,进而获得复合查询所涉及事件的边缘分布律,最后利用时间不确定事件查询处理技术进行后续的查询处理.实验证明了2种方法对时间不确定约束事件查询有效.基于事件约束优先查询处理方法的可能世界集规模更小,比基于可能世界的查询处理方法更高效.
Two approaches are proposed to process the constraint event stream with uncertain timestamps. The query processing approach based on possible worlds can obtain the results by scanning the possible worlds according to the semantic of the constraint events. The query processing approach based on constraint event priority calculates the joint probability density of event timestamps, furtherly, calculates the marginal probability density of events in the composited query, and finally processes the query according to the query processing technology for the uncertain timestamp events. Experiments verify that both the query processing approaches for constraint event streams with uncertain timestamps are effective, and due to the smaller possible worlds, the query processing approach based on constraint event priority is more efficient than the query processing approach based on possible worlds.
事件是RFID(radio frequency identification devices)系统的数据采集和管理形式,是CPS(cyber-physical system)及物联网中物理数据到逻辑语义的重要元素.随着RFID、CPS、物联网技术研究的不断深入,复杂事件处理技术研究也获得了广泛关注[1-3].目前,很多应用要求处理带有约束事件的复杂事件流.约束事件是指事件不是随机产生而是按照预定义的业务逻辑或规则产生,事件之间存在着约束关系[4].
很多系统[5-7]针对发生时间确定的事件流进行处理,通常假设事件流中的事件发生时间是精确的,并且来自不同事件源的事件能够汇集成一个全序或者偏序流.但是,数据的漏读和错读、系统采样时间粒度不匹配、分布式系统事件采集时间戳时钟同步等原因,都可能导致查询处理中事件发生时间未知或不精确.系统需考虑每个事件发生时间的所有可能情况,增加了查询复杂度. Zhang等[8]建立了基于时间不确定模型、模式查询语义及处理框架.有研究将时间戳不确定与空间不确定结合起来在事件流上进行序列模式的匹配[9].文献[10]提出了基于概率时间数据库模型用来清洗不确定时间事件.
本文研究的核心问题是在时间戳不确定的事件流中查询满足一定约束关系的事件处理,提出了基于可能世界的查询处理方法和基于事件约束优先的查询处理方法,利用实验验证这两个算法效率.
1 问题描述定义1 不确定原子事件.简称为不确定事件,本文的不确定事件特指发生时间不确定的原子事件.不确定事件可用元组(EventType, ID, UI:[lower, upper], (p: UI→[0, 1])?)表示,其中EventType为事件对应的类型;ID为事件唯一的识别信息;UI:[lower, upper]为事件提供者指定的事件发生的可能时间区间,lower为其左边界,upper为其右边界;p: UI→[0, 1]?为发生时间在区间UI上的可选的概率分布函数,默认的是均匀分布,此概率分布函数主要由事件源所决定.
通过UI和p可知,每个事件的发生时间有若干可能性,即在连续时间点,有如下关系式成立,{(tj, p(tj))∣j=1, …, |UI|, 0≤p(tj) ≤1, ∑p(tj)=1},其中,p(tj)是某一事件e发生在时刻tj的概率.
定义2 概率原子事件.简称为概率事件,是由不确定事件按照其所有可能发生的时刻及其概率转化而成的事件.概率事件可以用元组(ID, EventType, T, p)表示,其中p是不确定事件在T时刻发生的概率.
定义3 不确定事件流.由一系列不确定事件形成的组合,即UncertainS=(e1, e2, …, en),其中,下标为事件ID号.
定义4 概率事件流.由一系列概率事件按时间顺序形成的组合,即ProbabilityS=(e1t1, e2t2, …, entn),其中,下标为事件ID号,上标为事件发生的可能时刻.本文概率事件流是由不确定事件流转化而来. 图 1展示了不确定事件流转化成概率事件流.具体来说,图 1(a)是含有4个不确定事件的不确定事件流,而图 1(b)是由图 1(a)转化而来的,是含有16个概率事件的概率事件流.

|
图 1 获得概率事件流的过程 |
定义5 匹配事件集MES(matching event set).在事件流中,与指定复合事件模式Pa=(E1, E2, …, En)匹配的事件序列集.例如,MES(seq(E1, and(E2, E3), E4), S1))指的是在事件流S1中与嵌套事件模式(嵌套查询), seq(E1, and(E2, E3), E4)相匹配的事件序列集.
定义6 特征序列.特征序列是针对一个概率事件序列定义的,其定义为一个事件序列中具有的唯一的事件ID号序列.例如,概率事件序列(r11, s22, d33, w54, o66)的特征序列为(r1, s2, d3, w5, o6);同理,概率事件序列(r14, s26, d37, w58, o611)的特征序列同样为(r1, s2, d3, w5, o6).
定义7 事件约束(EC, event constraints).描述前、后事件间的依赖关系的规则,这种规则用于限制在某一事件发生后发生其它事件的可能性.这里包括两种EC,分别是发生约束(occurrence constraints)和顺序约束(order constraints).
这里使用的事件约束集为ECs.
ECs1:prior(Ei, Ej, he):=∀he, ¬(Ej[he]<Ei[he]),规定在任意事件序列中, Ej一定在Ei之后发生总是有效的.此约束属于顺序约束.
ECs2:exclusive(Ei, Ej, he):=∀he, Ei[he]→¬Ej[he], 规定在任意事件序列中, 如果Ei发生,Ej没有发生总是有效的.此约束属于发生约束.
ECs3:require(Ei, Ej, he):=∀he, Ei[he]→Ej[he], 规定在任意事件序列中, 如果Ei发生,Ej一定发生总是有效的.此约束属于发生约束.
EC的不确定事件查询QC是指在不确定事件流UncertainS中,查询并返回与事件模式Pa=(E1, E2, …, En)相匹配并满足ECs=(ECs1, ECs2, …, ECsm),而且其发生概率于ξ的事件序列及其概率值.即QC(Pa∧ECs,UncertainS,ξ) ={(d1, d2, …, dn),p(d1, d2, …, dn)| (d1t1, d2t2, …, dntn) ∈MES(Pa∧ECs, ProbabilityS), ∑p(d1t1, d2t2, …, dntn)=p(d1, d2, …, d2)>ξ}.其中,(d1t1, d2t2, …, dntn)为概率事件序列,(d1, d2, …, dn)为(d1t1, d2t2, …, dntn)等概率事件序列通过特征序列分组后对应的不确定事件序列(特征序列),∑p(d1t1, d2t2, …, dntn)为将对应相同特征序列(d1, d2, …, dn)概率事件序列的概率和.
2 基于可能世界优先的约束事件查询处理方法基于可能世界优先的查询处理方法(possibleF_QP),根据EC的不确定事件查询语义,通过对可能世界的遍历,获取查询结果.详细过程如下.
首先,根据目标不确定事件流UncertainS获得其概率事件流ProbabilityS,然后通过概率事件流ProbabilityS获得其可能世界集PWD(S),对每一个可能世界链pwdi进行EC检测和模式查询处理,获取满足EC且与查询模式Pa相匹配的概率事件序列seqi.最后计算每个满足条件的概率事件序列seqi发生的概率pi,将概率大于0的概率事件序列选择出来,形成概率事件序列候选结果集(CandResult).并扫描候选结果集中的所有概率事件序列seqi并按照其特征序列对候选结果集进行分组.将每组的概率事件序列的概率相加,若最终得到的概率值大于等于查询阈值ξ,则该分组的特征序列为查询结果,并记录下该序列的概率值;若最终得到的概率值小于查询阈值ξ,则舍弃该分组.
例如,针对图 2中的不确定事件流UncertainS=(d1, a2, b3, c4),进行复合模式Pa=seq(A, B, C)的查询,假定相关的ECs是prior(D, A, S).因为prior(D, A, S)所涉及的事件集为{A, D},复合模式Pa=seq(A, B, C)所涉及的事件集为{A, B, C},由此可求得两者的交集为{A},满足进行EC不确定事件查询的条件.然后,采用possibleF_QP对其进行EC的不确定事件查询处理.

|
图 2 事件流 |
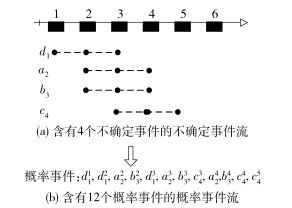
首先根据每个不确定事件的时间区间,进行流扩展,获得与不确定事件流相对应的概率事件流.即由含有4个不确定事件的不确定事件流转化成含有12个概率事件的概率事件流.转化过程见图 3.
|
图 3 获得概率事件流的过程 |
接下来,通过图 3(b)的概率事件流获得其对应的PWD(S)={pwd0, pwd1, pwd2, …, pwd79, pwd80}.对于∀pwdi∈PWD(S),进行模式Pa=seq(A, B, C)的匹配处理,同时,进行prior(D, A, S)的检测处理.获取满足EC且与查询模式Pa相匹配的概率事件序列seqi.最后计算每个满足条件的概率事件序列seqi的发生概率pi,将概率大于0的概率事件序列选择出来,形成概率事件序列候选结果集.例如,可能世界pwd4=(d11, a22, b33, c44)与模式Pa=seq(A, B, C)匹配,且满足prior(D, A, S),因此被放入候选结果集中;可能世界pwd1= (d11, a22, b32, c44)虽然满足prior(D, A, S),但是与事件模式Pa=seq(A, B, C)不匹配,因此不会被放入候选结果集中;可能世界pwd62= (d13, a22, b34, c45)虽然与事件模式Pa=seq(A, B, C)匹配成功,但是不满足prior(D, A, S),因此不会被放入候选结果集中;依次对可能世界进行模式Pa=seq(A, B, C)查询和prior(D, A, S)检测处理,最终获得候选结果集.由PWD(S)获得候选结果集的具体过程见图 4.

|
图 4 获得候选结果集的过程 |
获得候选结果集之后,计算其中每个候选结果的概率.根据与此查询相关的EC,计算出相关事件发生时间的联合分布.此例的相关事件是d1和a2,计算2个事件发生时间的联合分布律.为了计算事件d1和a2发生时间的联合分布律,首先根据prior(D, A, S)和事件d1和a2发生时间的概率质量函数计算其条件概率.获得条件概率P(a2.T|d1.T)的过程如下.
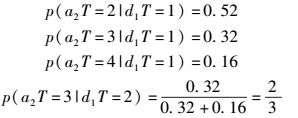
|

|
(1) |
然后根据联合概率计算的式(1) 和事件d1和a2发生时间的条件概率结果计算其联合概率分布.获得a2.T和d1.T的联合分布过程如下.
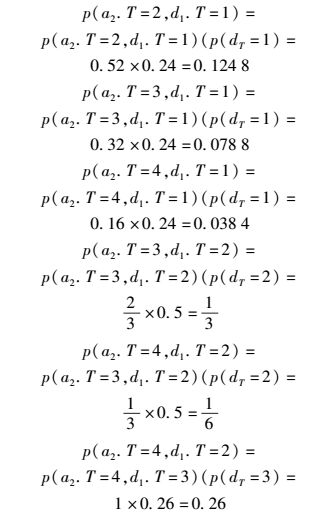
|
由上述计算结果形成事件d1和a2发生时间的联合分布律见表 1.得到事件d1和a2发生时间的联合分布律之后,计算候选结果集中每个候选结果的概率.由于事件d1、a2与事件b3、c4之间不存在EC,因此如果将事件d1、a2看作一个事件时,其与事件b3、c4三者之间就是彼此独立的,则可用式(2) 计算其概率.
|
|
表 1 a2.T和d1.T的联合分布律 |
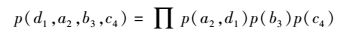
|
(2) |
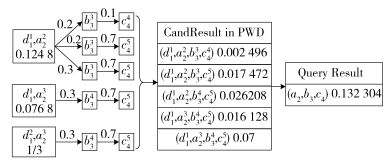
最后根据式(2) 计算每个候选结果的概率.例如候选结果(d11, a22, b33, c44)的概率为p(d11, a22, b33, c44)=0.124 8×0.2×0.1=0.002 496,同理,候选结果(d11, a22, b33, c45)的概率为p(d11, a22, b33, c44) =0.124 8×0.2×0.7=0.017 472.最终获得所有候选结果的概率.具体计算过程详见图 5.
|
图 5 获得查询结果的过程 |
接下来,计算模式查询结果的概率值.计算方法分两步,首先将候选结果按照其特征序列进行分组,然后按照式(3) 计算每个分组的特征序列的概率值.
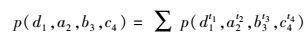
|
(3) |
其中,p(d1t1, a2t2, b3t3, c4t4)是一个分组中一个候选结果的概率值.按照特征序列可以将本例中候选结果集分成一个组,其特征序列(特征序列中只包含查询模式所涉及的事件)为(a2, b3, c4),其概率为p(a2,b3,c4)=p(d11,a22,b33,c44)+ p(d11,a22,b33,c45)+ p(d11,a22,b34,c45) + p(d11,a23,b34,c45) + p(d12,a23,b34,c45)=0.132 304.
最后,将每个分组的概率值和用户给定的查询阈值进行比较.该查询阈值由用户根据实际应用的精度要求以及实用经验给出.如果其概率值大于等于查询阈值,返回这个分组的特征序列及其概率值.如果其概率值小于查询阈值,淘汰该分组.至此,图 2中的事件流用possibleF_QP完毕.
possibleF_QP中,如果EC所涉及的事件和复合查询所涉及的事件的交集不为空,需要枚举此查询所涉及事件与EC所涉及事件发生时间的所有可能情况,假设EC所涉及的事件数为M,复合查询所涉及的事件数为N,事件的时间戳区间的平均大小为U,那么PWD(S)的大小是指数级的,即O(UN+M).如果在其上直接进行模式查询处理和EC检测,则计算的开销较大,为提高处理效率,需要对PWD(S)进行适当的约减,因此提出基于事件约束优先的查询处理方法.
3 基于事件约束优先的查询处理方法事件约束优先的查询处理方法(constraintsF_QP),即优先考虑复合查询所涉及的EC.该方法主要分三步完成.第1步,根据EC,计算其所涉及事件发生时间的联合分布律;第2步,基于事件发生时间的联合分布律,获得复合查询所涉及事件的边缘分布律,因为复合查询所涉及事件集和EC所涉及事件集的交集中的事件其发生时间的概率分布会有所改变,需要使用其边缘分布律;第3步,按照时间不确定事件查询处理技术进行后续的查询处理.下面以一个例子对constraintsF_QP进行详细的说明.
为了进行对比说明,同样以图 2中的事件流为例,用constraintsF_QP进行处理.首先进行第一步,根据prior(D, A, S),计算事件d1和a2发生时间的联合分布律,计算结果见表 1.

|
(4) |
然后,进行第二步,根据表 1中事件d1和a2发生时间的联合分布律和式(4),得到事件a2发生时间的边缘分布律,其边缘分布律见图 6.

|
图 6 事件a2发生时间的边缘分布律 |
复合查询所涉及事件集和EC所涉及事件集的交集中的事件,本例中即a2,其发生时间的概率质量函数会改变,变为其边缘分布律,然后将使用其边缘分布律作为其概率分布,事件a2发生时间的概率质量的改变详见图 7.

|
图 7 考虑事件约束的事件流 |
最后,进行第三步,按照两种时间不确定事件查询处理技术进行后续的查询处理.一种是基于点(point-based)的评估框架;一种是基于事件(event-based)的评估框架.首先使用第一种基于点的评估框架进行查询处理.
1) 基于点的评估框架,因为经典的复杂事件处理系统处理针对的是发生在确定的时间点的事件,因此在基于点的评估框架中,先将目标的时间不确定事件转化成带有概率的点事件,然后再用经典系统SASE[5]进行查询匹配处理,最后查询匹配候选结果按照特征序列进行分组,计算各组特征序列的发生概率,形成最终的查询匹配结果.
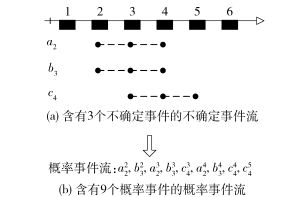
对于本例,首先对图 8(a)中的目标事件流进行流扩展,将含有3个不确定事件的事件流转化成含有9个概率事件的事件流,其转化过程见图 8,转化而成的概率事件流详见图 8(b).然后针对转化而成的概率事件流,获得PWD(S),见图 8(b). 图 9(a)为利用possibelF_QP得到的PWD(S),含有可能世界的数目是81,图 9(b)为利用constraintsF_QP得到的PWD(S), 含有可能世界的数目是27,通过图 9(a)和(b)比较可知,constraintsF_QP使得要进行复合查询处理的可能世界数比possibelF_QP要处理的可能世界数大大减少了,提高了处理效率.
|
图 8 获得概率事件流的过程 |

|
图 9 可能世界集的比较 |
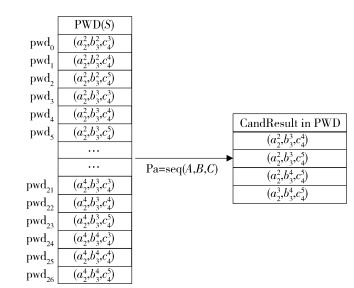
接下来,对图 9(b)的PWD(S)进行查询匹配处理.对于∀pwdi∈PWD(S),进行模式Pa=seq(A, B, C)的匹配处理,因为通过constraintsF_QP优先考虑EC,因此对PWD(S)进行处理不用进行EC检测.例如,可能世界(a22, b33, c45)与模式Pa=seq(A, B, C)匹配成功,会被放入候选结果集中;可能世界(a22, b32, c44)与事件模式Pa=seq(A, B, C)匹配不成功,不会被放入候选结果集中;对PWD(S)遍历,并进行模式查询,获得候选结果集.具体见图 10.
|
图 10 获得候选结果集的过程 |
得到查询的候选结果集后,需要计算候选结果集中每个候选结果的概率.由于事件a2与事件b3、c4之间不存在EC,因此如果事件a2、b3、c4三者之间彼此独立,则可用式(5) 计算其概率.

|
(5) |
最后根据式(5) 计算每个候选结果的概率.例如候选结果(a22, b33, c44)的概率为p(a22, b33, c44)=0.124 8×0.2×0.1=0.002 496,同理,候选结果(a22, b33, c45)的概率为p(a22, b33, c44)=0.124 8×0.2×0.7 =0.017 472.最终获得所有候选结果的概率.具体计算过程见图 11.
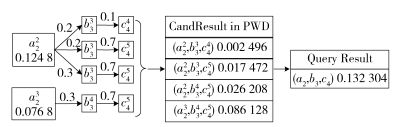
|
图 11 获得查询结果的过程 |
2) 基于事件的评估框架进行查询处理.首先对事件的发生区间进行约减,根据指定查询,确定每个时间不确定事件其时间区间的下界(lower endpoints);根据指定查询,确定每个时间不确定事件其时间区间的有效的上界;根据指定的查询窗口的约束,最后确定时间的上、下界.经过3次事件遍历,目标查询所涉及的事件,其时间区间的上、下界进行了重新确定.下面对图 2的事件流中的事件a2、b3和c4的时间区间进行上、下界的重新确定,具体过程如图 12所示.

|
图 12 获得事件发生区间的有效的上下界 |
对于本例,首先根据图 12中剪枝后的目标事件流进行流扩展,将含有3个不确定事件的事件流转化成含有6个概率事件的事件流,其转化过程见图 13(a),转化而成的概率事件流见图 13(b).
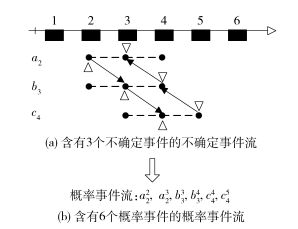
|
图 13 获得概率事件流的过程 |
图 14显示constraintsF_QP使得要进行复合查询处理的PWD(S)大大减少,降低了处理开销,提高了处理效率.

|
图 14 可能世界集的比较 |
实验评估查询长度、事件约束数目、事件数目、时间区间对所提出的基于possibleF_QP和基于constraintsF_QP的处理时间的影响.实验使用C++语言实现,运行环境为Intel(R) Core(TM) i7 3.07 GHz CPU、8.00 G内存和运行64位Windows7操作系统.仿照文献[8]模拟测试的做法,实现了一个事件流产生器,用事件流产生的事件对算法进行验证.
查询长度的影响.在事件约束数为1,时间区间为3,事件数为200时,评价查询长度(查询中包括的事件数量)对算法处理时间的影响,如图 15所示,查询长度的增长对possibleF_QP的影响较大,因为possibleF_QP在获取PWD(S)阶段,查询长度的增长使PWD(S)迅速增大,事件约束检测和复合查询的处理时间会显著增长.而constraintsF_QP的PWD(S)比较小,而且在查询处理的第3步,可以使用剪枝的方法进一步缩减可能世界的数目,因此处理时间的变化较possibleF_QP变化不大.

|
图 15 查询长度对处理时间的影响 |
事件数的影响.在事件约束为1,时间区间为3,查询长度为3时,评价事件数算法处理时间的影响.如图 16所示,事件数的增长,对possibleF_QP影响较大,而对constraintsF_QP影响较小,原因与查询长度影响实验相同.

|
图 16 事件数对处理时间的影响 |
事件约束数的影响.在时间区间为3,查询长度为5,事件数为200时,评价EC的数目对算法处理时间的影响.如图 17所示,随着EC数的增长,两种方法的处理时间都在增长,因为EC数目的增长可以导致概率计算代价增大. EC数的增长对possibleF_QP影响更大,因为possibleF_QP在获取PWD(S)阶段和候选集阶段,由于EC数的增长,EC检测时间会显著增长.而constraintsF_QP,只需进行查询处理,处理时间较possibleF_QP小.
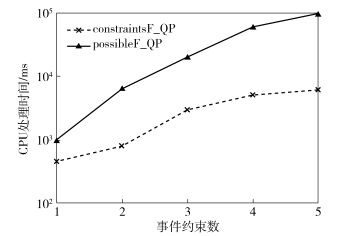
|
图 17 事件约束数对处理时间的影响 |
时间区间的影响.在EC为3时,查询长度为3,事件数为300时,评价时间区间对算法处理时间的影响.如图 18所示,时间区间的增长,对possibleF_QP影响较大,constraintsF_QP增长的幅度小于possibleF_QP.原因与EC数影响实验相同.

|
图 18 时间区间对处理时间的影响 |
本文研究了时间不确定模型下,具有约束的事件流查询问题.提出了基于可能世界优先的查询处理方法和基于事件约束优先的查询处理方法,并且实验证明两种方法对于处理事件约束查询都是有效的,事件约束优先的查询处理方法比基于可能世界优先的查询处理方法效率更高.
| [1] | Zhang H, Diao Y, Immerman N. On complexity and optimization of expensive queries in complex event processing[C]//SIGMOD2014. New York:ACM, 2014:217-228. |
| [2] | Ray M, Lei C, Rundensteiner E A. Scalable pattern sharing on event streams[C]//SIGMOD 2016. New York:ACM, 2016:495-510. |
| [3] | Poppe O, Lei C, Rundensteiner E A, et al. Context-Aware event stream analytics[C]//EDBT 2016. Konstanz:University Library, 2016:413-424. |
| [4] | Ding L, Chen S, Rundensteiner E A, et al. Runtime semantic query optimization for event stream processing[C]//ICDE2008. Washington, DC:IEEE Computer Society, 2008:676-685. |
| [5] | Gyllstrom D, Wu E, Chae H J, et al. SASE:complex event processing over streams[C]//CIDR2007. New York:ACM, 2007:407-411. |
| [6] | Welbourne E, Khoussainova N, Letchner J, et al. Cascadia:A system for specifying, detecting, and managing RFID events[C]//Proceedings of the 6th International Conference on Mobile Systems. New York:ACM, 2008:281-294. |
| [7] | Wang D, Rundensteiner E A, Iii R T E. Active complex event processing over event streams[J].Proceedings of the VLDB Endowment, 2011, 4(4): 634–645. |
| [8] | Zhang H, Diao Y, Immerman N. Recognizing patterns instreams with imprecise timestamps[J].Information Systems, 2013, 38(3): 244–255. |
| [9] | Yongluan Zhou, Chunyang Ma, Qingsong Guo, et al. Sequence Pattern Matching over Event Data with Temporal Uncertainty[C]//EDBT2014. Konstanz, Germany:University Library, 2014:205-216. |
| [10] | Maximilian Dylla, Iris Miliaraki, Martin Theobald. A temporal-probabilistic database model for information extraction[J].Proceedings of the Vldb Endowment, 2013, 6(14): 1810–1821. doi: 10.14778/2556549 |



