提出了一种新的基于非合作博弈的动态频谱分配方案,考虑多个蜂窝用户服务中心和具有认知能力的设备到设备(D2D)通信用户组,利用伯川德(Bertrand)博弈理论来解决用户频谱分配问题,分别对D2D对用户组和蜂窝用户服务中心的效用函数进行了改进,并给出了蜂窝用户服务中心的最优定价和D2D对用户组的动态价格调整策略,进一步证明了纳什均衡解的存在性和算法的收敛性.通过仿真实验,分析了不同蜂窝用户数和学习因子对所提出方案性能的影响.与现有结果进行比较显示,新方案在频谱利用率和系统公平性方面均有改进.
The author develops a new non-cooperative game dynamic spectrum allocation scheme. This scheme considers multiple cellular service providers and D2D service group which have the cognitive ability, and uses the Bertrand game theory to solve the problem of user spectrum allocation. The utility function of D2D service group and cellular service providers are improved respectively. This article also puts forward optimal pricing of cellular service providers and dynamic price adjustment strategy of D2D service group. Furthermore, the existence of a Nash equilibrium state and the convergence of the algorithm are proved. By simulation and experiment, the impact of different numbers of cellular users and different learning factors on the performance of the proposed scheme is analyzed. Compared with existing ones, this scheme improves both the spectrum utilization and system fairness.
设备到设备(D2D,device to device)通信模式允许在传统蜂窝网络中距离较近的移动设备直接进行通信[1],正在成为未来无线通信网络的发展方向.博弈论作为一种高效的资源分配工具,近几年来被广泛地应用于解决D2D通信网络中的资源分配问题[2-5].
针对认知D2D通信网络,最近,Kebriaei等[6]提出了一种基于买卖双方频谱的动态博弈模型,但是对博弈的稳定性分析不够充分,同时,没有考虑服务提供者之间出售频谱资源时的公平性问题.
笔者考虑多个蜂窝用户服务中心(CSP,cellular service providers)和具有认知能力的D2D对用户组,利用伯川德(Bertrand)博弈理论来解决用户频谱分配问题,分别对D2D对用户组和CSP的效用函数进行了改进,并给出了CSP的最优定价和D2D对用户组的动态价格调整策略.进一步,分析了博弈的稳定性,证明了纳什均衡解存在性和算法的收敛性.与文献[6]相比,考虑了D2D对用户组的满意程度和CSP频谱租借的公平性.其次与现有结果比较显示,提出方案在频谱利用率和系统公平性方面均有改进.
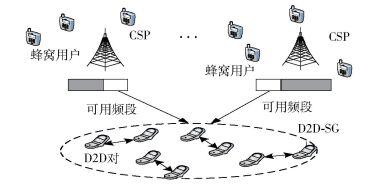
1 系统模型系统模型如图 1所示.假设系统中有N个CSP,1个D2D对用户组(D2D-SG,D2D service group). CSP有Mn个频谱数量,其工作频段为fn. D2D对用户组可以在对CSP不产生干扰时共享空闲频谱,CSP以价格pn单位带宽租出空闲频谱μn给D2D对用户组.
|
图 1 频谱共享的网络模型 |
在D2D对用户组选择了传输模式后,可以根据信道的参数来调节传输速率.误码率为
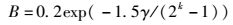
|
其中,γ为信噪比,频带利用率为k,且k为正值.为了保证信息的传输质量,比特的错误概率的门限值为Btar.假设采用的是正交振幅调制(QAM,quadrature amplitude modulation)方式则频带利用率
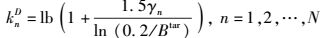
|
(1) |
由于D2D对用户组会向周围的所有CSP发起频谱租赁的请求,CSP结合自身的利益,竞相租借频谱给D2D对用户组,在CSP间形成了频谱价格博弈.当到达纳什均衡的时候,CSP就获得了额外的效益,而服务中的蜂窝用户的通信不会受到干扰,D2D对用户组也实现了自身通信,利用租借的频谱实现了频谱共享,并且更好地提高了利用率.
2 基于博弈论的频谱共享算法2.1 D2D对用户组的效用函数CSP要价和D2D对用户组的需求频谱数量相关,Huang等[7-8]给出了相应博弈效用函数,但未考虑到D2D对用户组自身频谱需求量对效用函数的影响.
首先介绍频谱利益Φ(bn),它与D2D对用户组租借的频谱量呈现对数关系,表达式为
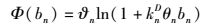
|
(2) |
其中:bn为CSPn的空闲频谱大小,knD为D2D对用户组租借频谱的利用率.

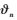
θn(0≤θn≤1) 为满意度参数,表示D2D对用户组租借CSP的频谱资源时满意程度.如果D2D对用户组在CSPn上所预期获得的频谱μn比CSP n+1上所获得的μn+1多,则此时满意水平为θn>θn+1.
以频谱利益为基础,提出了新的D2D对用户组频谱需求的二次效用函数为
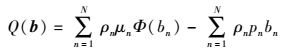
|
(3) |
其中:b为D2D对用户组在各个CSP租借的频谱量. pn为CSPn的租借频谱价格,ρn表示D2D对用户组是否租借CSPn上的频谱资源,ρn=1表示选择租借,否则不购买此中心频谱(ρn=0).
2.2 CSP的效用函数和最优定价在该系统中,CSP的策略是各自的出价pn,其效用函数的公式为
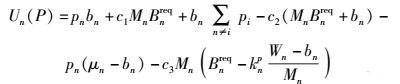
|
(4) |
其中:c1为CSP租借空闲频谱的价格;c2为CSP频谱成本价格;c3为其未满足蜂窝用户频谱要求的惩罚因子;Bnreq为使得蜂窝用户能够连接到服务器时需要的频谱带宽,Wn、Mn以及knp为CSPn的带宽、蜂窝用户数目和频带利用率,knp受基站位置、采用的调制技术和基站分布密度共同影响,knp=Bnreq/(Wn/Mn),bn是共享给D2D用户的频谱数量. P是博弈方售出空闲频谱价格的集合,P={p1, p2, …, pN}.
式(4) 中,第1、2项主要是服务D2D和蜂窝用户的时候获得的收益,第3项是CSPn和其他CSP价格差异的收益,第4项代表此服务中心自身频谱的成本,最后两项主要是对不能满足D2D对用户频谱需求和蜂窝用户服务质量要求的惩罚.
纳什均衡用最大反应函数来获得,当其他CSP出价P-n时,CSPn的策略是
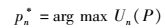
|
(5) |
策略集合P*={p1*, …, pN*}是竞价博弈的纳什均解,求解过程如下:
假设D2D对用户组购买CSPn的频谱. Q(b)对bn求偏导得
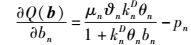
|
(6) |
令式(6) 为0,得Q(b)最大时最优频谱租借量为
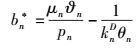
|
(7) |
将式(7) 代入式(4),让Un(P)只含变量参数pn,然后,将Un(P)对pn求一阶导数,可得
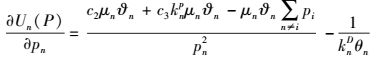
|
(8) |
令
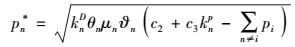
|
(9) |
假设定义pn(t)为CSPn在第t次迭代后的频谱租借价格,类似定义集合Pn(t)和P-n(t).接下来介绍CSP策略选择的两种情况.
情况1 在前几次迭代过程中,CSP之间是知道彼此的价格策略的,第t次采取的策略为Pn(t),所以CSPn在第t+1次迭代时有
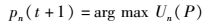
|
(10) |
情况2 在多种情况下,某一个CSP不知道其他用户的策略信息,为了使自身的利益最大化,只能通过频谱需求和相关信息来调整自己的策略.使用迭代方法,则CSP的策略调整为

|
(11) |
其中αn为学习速率调节因子(简称学习因子).
2.4 纳什均衡分析纳什均衡解存在性定义:有N个参与者参加了博弈,令P=P1×P2×…×PN为所有参与用户的行为空间,当任意x、y∈P,使得下列条件成立:
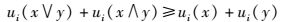
|
(12) |
则其效益函数ui(·)就符合此博弈的要求,式(12) 中x∨y=max (x, y),x∧y=min (x, y).特别地,当u(·)二次可微,其在x∈P情况下,满足

|
(13) |
那么此博弈有一个纳什均衡.
根据式(8) 可知Un(P)对pn的一阶导数,对式(8) 继续求pn的偏导有

|
(14) |
由于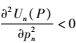
动态博弈算法的稳定性能使博弈算法最终收敛于纳什均衡.博弈的稳定性需要通过对雅克比(Jacobian)矩阵的特征值进行分析得到,式(11) 所对应的Jacobian矩阵表示为

|
(15) |
在有2个CSP的博弈系统中,情况1中算法的Jacobian矩阵为
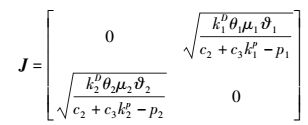
|
(16) |
在情况1中,令矩阵中元素的分母大于分子,就可以使Jacobian矩阵中的行、列元素分别都小于1,最终趋于平稳.
在情况2中,每个CSP不可知其他CSP的策略信息,价格调整的速度直接受学习因子影响,并且变化趋势相同.对2个蜂窝用户的Jacobian矩阵分析如下.
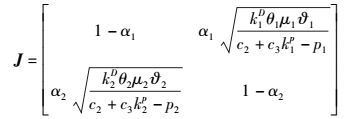
|
(17) |
由于,式(17) 中的Jacobian矩阵不是对角矩阵,也不是上三角矩阵或者下三角矩阵,所以,根据特征方程来求得相应的特征值.特征方程为
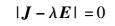
|
(18) |
即

|
(19) |
可求得其特征值分别为
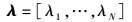
|
(20) |
由定义可知,如果Jacobian矩阵的特征值都在复平面的单位圆内,即满足|λn|<1,就能确定这个自映射函数满足动态博弈的稳定性条件.因此,由学习因子αn、满意水平度θn、向CSP租借的频谱μn和频谱平均值相似度μ共同决定情况2中的频谱共享算法.当已知以上的参数时,就可以根据纳什均衡状态来确定学习速率调整因子αn的值.
3 仿真结果及分析考虑认知D2D网络中存在3个CSP和1个D2D对用户组的情况,每个服务器都有多个正在服务的蜂窝用户或者D2D对. 3个CSP在频谱市场上可以租借的最大频谱资源分别是150 MHz、200 MHz和300 MHz,假设每个蜂窝用户在以上的3个服务器预订需要的频谱带宽分别是10 MHz、15 MHz和20 MHz,也就是Breq=(10; 15; 20). D2D对用户的目标误比特率为Btar=10-4. CSP出租单位的频谱所得到利益以及付出代价的因子参数分别为c1=10和c2=15.另外,定义网络中的频谱利用率为

|
其中:Bnp和Bnd代表CSPn中所有蜂窝用户和D2D对用户组的频谱带宽,Bn为其可以提供最大的频谱带宽资源,假设满意水平θ1=θ2=θ3=θ.
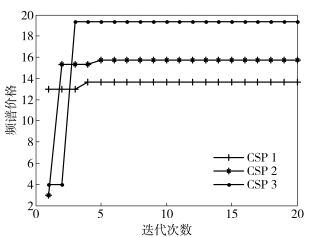
图 2显示了3个CSP的售价迭代收敛的过程.可知,3个CSP的频谱索要的市场价格随着迭代次数的增多而渐趋于平稳,最后达到纳什均衡.
|
图 2 价格纳什均衡的收敛 |
从图 3中可知,随着服务中心中正在服务蜂窝用户的数目增多,3个服务中心租借给D2D对用户组的市场价格也随着增大.这是由于蜂窝用户的增多会加大对服务中心频谱资源的需求,而现有的频谱资源有限,使得服务器为了满足蜂窝用户的频谱需求而减少对D2D对用户组的出租,同时提高市场租借的价格.另外,由图 3也可以看出,CSP对D2D对用户组出售频谱价格和D2D对用户组的满意度有关.当满意度降低时,D2D对用户组会减少对频谱的购买,CSP就会通过降低市场出售价格来激励D2D对用户组租用和购买频谱,进而提升自身的收益.

|
图 3 不同蜂窝用户数目下的价格变化 |
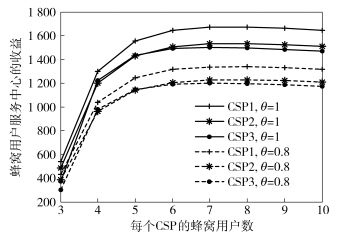
由图 4可知,3个CSP的收益会随着蜂窝用户数目的增大逐渐得到提升,最终逐渐平稳.这是因为一开始蜂窝用户的数目不是很多,CSP可以满足蜂窝用户频谱的需求量,使得其受到的惩罚不很明显,所以会给服务中心带来更多的收益.然而,随着蜂窝用户的大量增多,蜂窝用户需要大量的频谱,此时,CSP因为租借频谱给D2D对用户组,而不能满足蜂窝用户频谱量的需求,就会受到相应的惩罚.所以,服务中心的收益会达到饱和状态.同时,由图 4可知,如果D2D对用户组对租用频谱的满意度不高,就会减少购买频谱的数量,使得CSP收益降低.
|
图 4 不同蜂窝用户数目下的收益变化 |
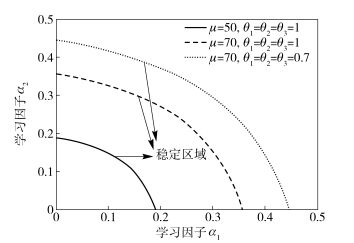
根据式(15) 和式(17) 分析可知学习因子α1和的α2关系,仿真得到它们的稳定域,这里只针对其中的2个CSP进行分析.分析图 5可知,学习因子所处的稳定范围和D2D对用户组预期借用的频谱数量和满意程度有关.如果预期要租用的频谱越多,就会出现较大稳定的范围;对服务中心的满意程度越高,稳定性就越小.
|
图 5 学习因子稳定范围 |
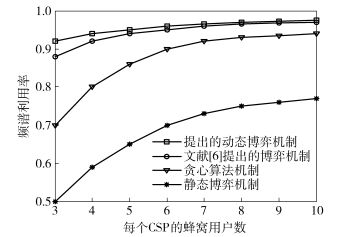
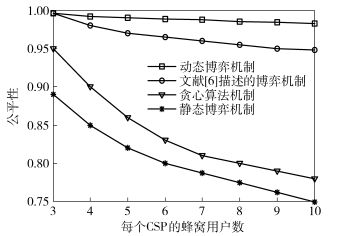
图 6和图 7给出所提出算法与文献[6]、贪心算法、静态博弈3种方案的频谱利用率和公平性随着蜂窝用户数目的变化趋势.由图 6可知,提出的博弈模型在不同蜂窝用户数目下都能保持较高的频谱利用率,相比其他3种模型有较好的性能.由图 7可知,随着蜂窝用户数目增多,其他3种方案的公平性下降较快,而所提出算法能保持较好公平性,这是由于所提出代价函数的惩罚因子可以很好地降低CSP盲目地出售频谱.由此可知,提出的博弈方案的公平性要优于其他方案,且鲁棒性好,更适用于蜂窝用户数目多的网络.
|
图 6 4种博弈算法的频谱利用率 |
|
图 7 4种博弈算法的公平性 |
针对目前认知D2D通信中多个CSP竞争共享频谱资源给D2D用户的频谱分配算法研究较少的问题,运用非合作博弈模型分析了认知D2D通信中蜂窝用户间和D2D对用户组之间的博弈,提出了一种新的基于非合作博弈的动态频谱分配方案.考虑到不同蜂窝用户数情况下的要价及利润所产生的影响,改进了蜂窝用户和D2D对用户组的收益函数,讨论了在不同学习因子影响下动态博弈算法的收敛速度和博弈的稳定性,分析了不同蜂窝用户数目下的频谱利用率和公平性性能,仿真实验验证了所提出改进方案的有效性.
| [1] | Xu Chen, Song Lingyang, Han Zhu, et al. Efficiency resource allocation for device-to-device underlay communication systems:are verse iterative combinatorial auction based approach[J].IEEE Journal on Selected Areas in Communications, 2012, 31(9): 348–358. |
| [2] | Xu Chen, Song Lingyang, Han Zhu, et al. Interference-aware resource allocation for device-to-device communications as an underlay using sequential second price auction[C]//2012 IEEE International Conference on Communications (ICC). Ottawa, Canada:IEEE, 2012:445-449. |
| [3] | Yin Rui, Yu Guanding, Zhong Caijun, et al. Distributed resource allocation for D2D communication underlaying cellular networks[C]//2013 IEEE International Conference on Communications (ICC). Budapest, Hungary:IEEE, 2013:138-143. |
| [4] | Huang Jun, Yin Ying, Sun Yi, et al. Game theoretic resource allocation for multicell D2D communications with incomplete information[C]//2015 IEEE International Conference on Communications (ICC). London, UK:IEEE, 2015:3039-3044. |
| [5] | Niyato D, Hossain E. Competitive pricing for spectrum sharing in cognitive radio networks:dynamic game, inefficiency of Nash equilibrium, and collusion[J].IEEE Journal on Selected Areas in Communications, 2008, 26(1): 192–202. doi: 10.1109/JSAC.2008.080117 |
| [6] | Kebriaei H, Maham B, Niyato D. Double sided bandwidth-auction game for cognitive device-to-device communication in cellular networks[J].IEEE Transactions on Vehicular Technology, 2016, 65(9): 7476–7487. doi: 10.1109/TVT.2015.2485304 |
| [7] | Huang Jun, Sun Yi, Chen Qianbin. Gallery:a game-theoretic resource allocation scheme for multicell device-to-device communications underlaying cellular networks[J].IEEE Internet of Things Journal, 2015, 2(6): 504–514. doi: 10.1109/JIOT.2015.2419632 |
| [8] | Huang B Y, Su S T, Wang C Y, et al. Resource allocation in D2D communication-a game theoretic approach[C]//2014 IEEE International Conference on Communications (ICC). Sydney, Australia:IEEE, 2014:483-488. |


