为了研究在各向同性散射和非各向同性散射中信道的传输特性,建立一种椭圆散射信道模型,同时在发射端和接收端设置均匀线性阵列以研究多输入多输出系统性能.假设波达信号到达角服从Von Mises分布,在定量给出到达角和发射角关系的条件下分析了参考模型的相关函数和信道容量.另外,在精确多普勒扩展法的基础上提出一种改进的参数计算方法,在参考模型的基础上得到了仿真模型,模型的数值结果阐明了Von Mises分布下信道的相关特性.理论分析和仿真结果表明,信道仿真器和参考模型有近乎一致的时间相关性,同时该模型的提出也拓展了空间统计信道模型的研究.
To study the transmission characteristics of the channel under isotropic and non-isotropic scattering environments, a geometric elliptical scattering model was established. Both the transmitter and receiver are adapted uniform linear array to research multiple-input multiple-output performance. First, assume that the angle of arrival (AOA) obey Von Mises density distribution. In the quantitative analysis of the relationship between AOA and angel of departure, the time auto correlation function, the spatial correlation function of the reference model are analyzed, so as the channel capacity. In addition, a parameter calculation method based exact doppler spread was proposed, and a simulation model was obtained based on a reference model. The statistics of the proposed model illustrates the influence of the characteristic of the channel model under the Von Mises distribution. Analysis and simulation show that the channel simulator and the reference model have almost the same time correlation function, and this model also extends the research of spatial statistical channel model.
建立准确真实的多输入多输出(MIMO, multiple-input multiple-output)信道模型对于设计和评估MIMO无线通信系统的性能十分重要,特别是运用MIMO技术的宽带无线通信系统,就需建立适当的信道模型研究其时间、空间及频率相关特性.过去提出的单环模型[1-2]和双环模型[3]主要适用于建立窄带MIMO信道模型.与单环模型、双环模型相反,椭圆散射模型是专门用于建模宽带MIMO信道的一类经典模型.因此,在椭圆散射信道模型的基础上提出一种MIMO信道模型.
信道仿真器能够通过产生多个不相关的瑞利衰落波来仿真MIMO信道[4]、宽带衰落信道[5]和组合衰落信道,易于实现.在过去的研究中已经提出了一些参数计算法[6-8]如Jakes法[8],精确多普勒扩展法(MEDS, exact Doppler spread)[6, 8],但是Jacks法得到的统计特性并不是很理想,而MEDS法的一个缺点就是当需要产生4个以上不相关的瑞利衰落过程时就需要大量的正弦波,这增加了模型的复杂性也限制了信道仿真器的运用[8].确定性信道仿真器能够产生多个不相关的瑞利衰落波形避免使用大量的正弦波,据此提出一种基于MEDS法的新的参数计算方法.
在椭圆散射模型中,通过假设波达信号的到达角服从Von Mises分布,笔者研究了散射体的各向同性散射和非各向同性散射对信道传输特性的影响,然后利用发射角和达到角之间的关系得到了参考模型的相关函数;最后在MEDS法的基础上提出一种改进的参数计算方法,得到确定性信道仿真器.与随机信道仿真器相比[7]确定性信道仿真器有更好的仿真效率且与参考模型的理想时间特性相似.
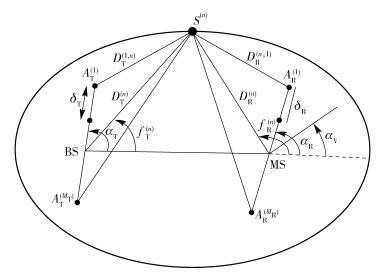
1 几何椭圆散射模型从图 1所示的几何椭圆散射模型导出MIMO信道模型,具有相同传播路径长度的所有散射体S(n)(n=1, 2, …, N)都分布在一个椭圆上,基站(BS, base station)和移动台(MS, mobile station)分别是椭圆的2个焦点,椭圆的长半轴和短半轴分别是a和b,BS和MS之间的距离是2f.假设发射端BS和接收端MS分别由MT和MR个均匀线性天线阵列组成. αT(αR)分别表示发射(接收)天线阵列的倾斜角度,δT(δR)分别表示发射(接收)天线元素之间的间距,考虑到天线尺寸远远小于模型参数a和f,所以有不等式(MT-1)δT≪a-f,(MR-1)δR≪a-f成立,x轴和运动方向之间的夹角用αV表示,发射角(AOD, angel of departure)用φT(n)表示,到达角(AOA, angle of arrival)用φR(n)表示(n=1, 2, …, N).
|
图 1 几何椭圆散射模型 |
根据图 1所示的几何椭圆散射模型导出MIMO参考信道模型,参考模型是在假设局部散射体S(n)趋于无穷的情况下得到的,因此第k个接收天线AR(k)是由无穷多数量的平面波叠加而成.根据图 1,BS端AT(l)与MS端AR(k)之间的传输链路的复增益可表示为

|
(1) |
其中:En和θn分别表示由于局部散射体S(n)的相互作用引起的增益和相位,KR(n)表示指向第n个接收平面波的传播方向的波矢向量,rR表示接收机的空间平移向量,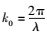

相位KR(n)rR表示由于接收机的移动引起的相位,可表示为

|
(2) |
其中fmax表示最大多普勒频移.
k0Dn表示总的传输距离引起的相位,可表示为

|
(3) |
其中:DT(l, n)表示从AT(l)到S(n)之间的距离,DR(n, k)表示S(n)到AR(k)之间的距离,由于(MT-1)δT≪a-f,
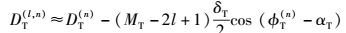
|
(4) |

|
(5) |
如图 1所示,DT(n)和DR(k)分别表示BS到S(n)距离和S(n)到MS的距离.
把式(2)~式(5) 代入式(1) 中就可以得到参考模型第l根发射天线AT(l)到第k根接收天线AR(k)传输链路的复信道增益gkl(t):

|
(6) |
其中
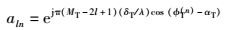
|
(7) |

|
(8) |

|
(9) |
分析式(6) 中复信道增益gkl(t),根据中心极限定理gkl(t)服从均值为零方差为1的复高斯随机过程.因此,gkl(t)的包络|gkl(t)|服从瑞利分布.
在参考模型中,定量给出AOA和AOD之间的关系,AOD(φT(n))可用AOA(φR(n))表示为[8]

|
(10) |
其中
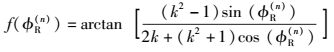
|
(11) |

传输链路AT(l)-AR(k)和链路AT(l′)-AR(k′)的空间-时间互相关函数定义为信道增益gkl(t)和gk′l′*(t)之间的相关性,即
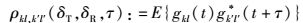
|
(12) |
其中E{·}表示求期望,将式(6) 代入式(12) 中并对随机变量θn求平均,可以得到空间-时间互相关函数:

|
(13) |
其中

|
(14) |

|
(15) |
接着要计算随机变量φT(n)的统计均值,当散射体的数量接近于无穷时,离散随机变量φT(n)和φR(n)就会变成连续随机变量φT和φR,φT仍然是φR的函数.微分角度dφR无穷小的能量与PφR(φR)dφR是成比例的,PφR(φR)表示φR的概率分布,当N→∞时,这个无穷小分布就趋向于1/N,即1/N=PφR(φR)dφR.根据式(13) 参考模型三维空间-时间互相关函数可表示为

|
(16) |
其中
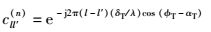
|
(17) |
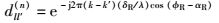
|
(18) |

|
(19) |
为了研究在各向同性和非各向同性两种环境中参考模型的时间自相关函数rkl(τ)和空间互相关函数ρkl, k′l′(δT, δR),假设波达信号AOAφR服从Von Mises分布[9],Von Mises分布函数的表达式为
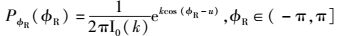
|
(20) |
其中:I0(·)表示第一类零阶修正的贝塞尔函数[9-10],u∈(-π, π]表示到达角度φR的均值,参数k≥0控制角度谱的形状,用k的不同取值来分别表示各向同性散射和非各向同性散射:在各向同性散射中k=0,PφR(φR)=1/2π,此时Von Mises退化成均匀分布;用参数k≠0的Von Mises分布表示非各向同性散射.
复信道增益的时间自相关函数(ACF, auto correlation function)rkl(τ)定义为rkl(τ):=E{gkl(t)gkl*(t+τ)},时间ACFrkl(τ)可通过设置天线阵列间距δT和δR为零得到,即rkl(τ)=ρkl, k′l′(0, 0, τ),所以rkl(τ)可表示为
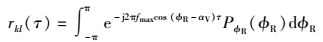
|
(21) |
对所有满足k=1, 2, …, MR和l=1, 2, …, MT传输链路AT(l)-AR(k)都具有相同的时间自相关函数,在各向同性散射环境中角度P(φR)服从均匀分布,即PφR(φR)=1/2π,此时时间自相关函数可表示为rkl(τ)=I0(2πfmaxτ).
同样空间互相关函数ρkl, k′l′(δT, δR)定义为ρkl, k′l′(δT, δR):=E{gkl(t)gk′l′*(t+τ)},也等于互相关函数ρkl, k′l′(δT, δR, τ)当τ等于零时候的值,即ρkl, k′l′(δT, δR, τ)=ρkl, k′l′(δT, δR, 0),因此空间互相关函数ρkl, k′l′(δT, δR)可表示为

|
(22) |
信道容量通常是衡量MIMO系统的重要指标之一,为使信道容量最大化,最优的策略是将功率平均分配到各天线阵元上,此时信道的平均容量可表示为[11]

|
(23) |
其中:INr表示Nr维的单位矩阵,p/σ2表示信噪比,Nt表示发射天线的数量,MIMO信道矩阵H可表示为H=Rr1/2Hw(Rt1/2)T,Rr表示接收端阵元间相关矩阵,Rt表示发射端阵元间相关矩阵,在不考虑发射端相关性的条件下,Rt可认为是单位矩阵,Hw是同分布的复高斯随机矩阵.
3 确定性信道仿真器在各向同性散射环境中,复信道增益gkl(t)服从均值为0方差为1的复高斯过程,因此|gkl(t)|服从瑞利分布,此时参考模型的时间自相关函数为rkl(τ)=J0(2πfmaxτ),信道仿真器的目的就是要尽可能产生接近参考模型时间自相关函数的理想统计特性.
根据中心极限定理[9],一个高斯随机过程可近似为大量正弦波的叠加.根据这个定理,信道仿真器的第l条瑞利衰落过程可表示为

|
(24) |
其中
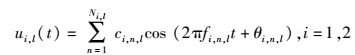
|
(25) |
其中:Ni, l表示正弦波的叠加数量,ci, n, l,fi, n, l和θi, n, l分别表示增益、离散频率和相位.模型的参数在仿真时必须是定值,这就意味着ui, l(t)是一个确定性的函数,ui, l(t)自相关函数的时间平均值可表示为

|
(26) |
根据精确多普勒扩展法提出一种改进的参数计算方法来确定离散频率分量fi, n, l值.在MEDS法中,离散频率分量可表示为

|
(27) |
改进的MEDS法的离散频率分量可表示为
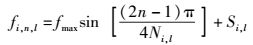
|
(28) |
其中:Si, l应该选取无穷小的正数,增益ci, n, l=σ0
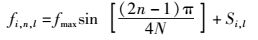
|
(29) |
接下来讨论Si, l值对近似等式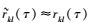
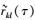

|
(30) |
其中τmax表示最大的时间间隔,根据参考文献[11],τmax=N/(2fmax)是一个合适的值.
4 仿真结果用MS端AOAφR服从Von Mises分布,通过数值计算和仿真,给出散射体在各向同性和非各向同性中时间自相关函数rkl(τ)和空间互相关函数ρkl, k′l′(δT, δR)的仿真结果.
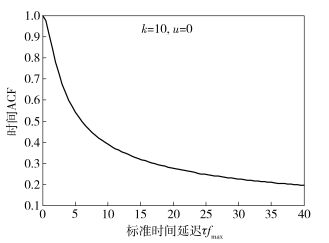
图 2所示为k=0时,Von Mises分布退化为均匀分布,即各向同性散射环境中时间自相关函数rkl(τ). 图 3所示为φR服从参数为k=10,u=0的Von Mises分布,即非各向同性散射环境中时间ACFrkl(τ).通过图 2和图 3比较可发现,在各向同性散射中时间ACF震动下降趋于0,而在非各向同性散射中时间ACF平稳下滑最终稳定在0.2左右.

|
图 2 各向同性散射中参考模型时间自相关函数 |
|
图 3 各向异性散射中参考模型时间自相关函数 |
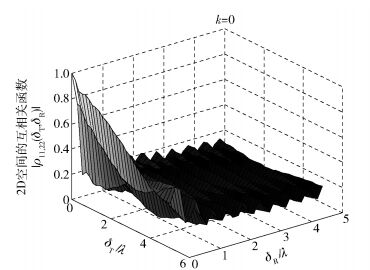
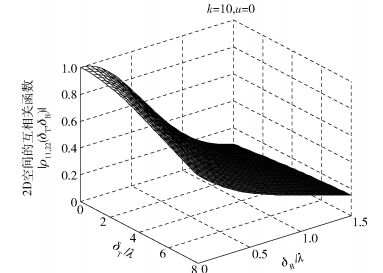
图 4所示为φR服从k=0时的Von Mises分布,即各向同性散射环境中空间互相关函数ρkl, k′l′(δT, δR);图 5所示为φR服从参数k=10,u=0的Von Mises分布,即非各向同性散射环境中空间互相关函数ρkl, k′l′(δT, δR).由图 4可发现,空间互相关函数ρkl, k′l′(δT, δR)在δT=δR=0时最大为1,随着阵元间距δT和δR的增加,空间相关性减少并趋于0.比较图 4和图 5可发现,和时间自相关函数变化规律一样,参数k影响角度谱的形状,均匀分布时即各向同性散射中空间互相关函数震荡快速衰减为0,非各向同性散射中2D空间互相关函数平滑衰减到0.
|
图 4 各向同性散射中空间互相关函数 |
|
图 5 各向异性散射中参考模型空间互相关函数 |
在计算MIMO信道容量时,假设发射端和接收端是由4×4的均匀线性阵列组成. 图 6给出了参数k对信道容量的影响.从图 6中可看出,当0≤d/λ≤0.4时,信道容量几乎呈线性上升,当d/λ≥0.4时,信道容量在某个稳定的范围内保持不变,这是因为随着阵元间距的变大,阵元间的相关系数变小,从而使信道容量快速增大,当阵元间距增加到一定范围时,相关系数不再明显变化,使得信道容量也基本保持不变,这一结论与文献[12]的研究结果一致,从而验证了信道模型特性的正确性.图中还表示了k=0时,Von Mises退化为均匀分布,此时信道容量最大,随着值增加,信道容量减小,这说明散射体在各向同性散射环境中的信道容量要大于在非各向同性散射环境中的信道容量.

|
图 6 参数k对MIMO信道容量的影响 |
图 7所示为正弦波叠加数量N对均方根误差的影响,均方根误差Ei, l是关于Si, l的函数,对于给定的正弦波叠加数量N,Ei, l随着Si, l绝对值的增加而增加,当Si, l=0时,均方根误差最小为0.当增加正弦波叠加数量N时,相应的均方根误差也会减小.

|
图 7 不同叠加数量N下的均方误差函数 |
由图 7的仿真结果可看出,为了得到较小的均方值误差,Si, l应该选择尽量小的值. 图 8所示为不同的Si, l值对参考模型和用改进的多普勒扩展法得到的仿真模型的时间自相关函数值的对比,从比较结果可看出,当Si, l=0时,仿真模型和参考模型具有很好的一致性,当Si, l=±16×10-7时,用改进的多普勒扩展法计算得到的仿真模型具有相同的时间自相关函数.图中显示当fmaxτ<10时,参考模型和仿真模型具有相同的时间特性,当fmaxτ>10时,参考模型和仿真模型的时间自相关函数会逐渐分离,并不再重合.所以在时间延迟比较长的情况下,为了使仿真模型的时间相关特性与参考模型的理想特性一致,应当增加正弦波叠加数量N.

|
图 8 参考模型和信道仿真器的时间自相关函数曲线 |
从几何椭圆散射模型出发,假设有无穷多数量的散射体位于椭圆上,得到了参考信道模型,推导出了空间-时间互相关函数、时间自相关函数、空间互相关函数的解析表达式,用MS端AOAφR服从Von Mises分布来描述散射体的各向同性散射和非各向同性散射.在各项同性散射中,Von Mises退化为均匀分布,用参数k=10的Von Mises分布刻画非各向同性散射,同时比较了在两种散射环境中的相关函数.比较结果发现,各向同性散射环境中相关函数震荡衰落趋于稳定,非各向同性散射环境中相关函数平缓下降趋于稳定.同时在参考模型的基础上用改进的多普勒扩展法得到了仿真模型,并且在各向同性散射中比较了参考模型和仿真模型的时间自相关函数,仿真结果表明得到的信道仿真器的相关特性与理想参考模型的相关特性近乎一致.提出的椭圆散射信道模型特别适合于基站天线位置较低的微蜂窝通信系统,同时此模型的提出拓展了空间统计信道模型的研究,也是得出确定性信道仿真模型的基础.
| [1] | Byers G, Takawira F. Spatially and temporally correlated MIMO channels:modeling and capacity analysis[J].IEEE Transactions on Vehicular Technology, 2004, 53(3): 634–643. doi: 10.1109/TVT.2004.825766 |
| [2] | Mecklenbrauker C F, Molisch A F, Karedal J, et al. Vehicular channel characterization and its implications for wireless system design and performance[J].Proceedings of the IEEE, 2011, 99(7): 1189–1212. doi: 10.1109/JPROC.2010.2101990 |
| [3] | Zajic A G, Stuber G L. Space-time correlated mobile-to-mobile channels:Modelling and simulation[J].IEEE Transactions on Vehicular Technology, 2008, 57(2): 715–726. doi: 10.1109/TVT.2007.905591 |
| [4] | Sterian C E D, Wang C X, Johnsen R, et al. Rotationally invariant space-time trellis codes with 4-D rectangular constellations for high data rate wireless communications[J].Journal of Communications and Networks, 2004, 6(3): 258–268. doi: 10.1109/JCN.2004.6596582 |
| [5] | Yip K W, Ng T S. Karhunen-Loeve expansion of the WSSUS channel output and its application to efficient simulation[J].IEEE Journal on Selected Areas in Communications, 1997, 15(4): 640–646. doi: 10.1109/49.585774 |
| [6] | Patzold M, Hogstad B, Youssef N. Modeling, analysis, and simulation of MIMO mobile-to-mobile fading channels[J].IEEE Transactions on Wireless Communications, 2008, 7(2): 510–520. doi: 10.1109/TWC.2008.05913 |
| [7] | Gutierrez C A, Patzold M. The design of sum-of-cisoids rayleigh fading channel simulators assuming non-isotropic scattering conditions[J].IEEE Transactions on Wireless Communications, 2010, 9(4): 1308–1314. doi: 10.1109/TWC.2010.04.091198 |
| [8] | Zajic A G, Stuber G L. Efficient simulation of Rayleigh fading with enhanced de-correlation properties[J].IEEE Transactions on Wireless Communications, 2006, 5(7): 1866–1875. doi: 10.1109/TWC.2006.1673098 |
| [9] | Abdi A, Kaveh M. A space-time correlation model for multielement antenna systems in mobile fading channels[J].IEEE Journal on Selected Areas in Communications, 2006, 20(3): 550–560. |
| [10] | Cheng X, Wang C X, Laurenson D I, et at. An adaptive geometry-based stochastic model for non-isotropic MIMO mobile-to-mobile channels[J].IEEE Transactions on Wireless Communications, 2009, 8(9): 4824–4835. doi: 10.1109/TWC.2009.081560 |
| [11] |
周杰, 王亚林, 罗宏, 等. MIMO阵元方向性对系统性能影响的研究[J]. 华中科技大学学报(自然科学版), 2015, 43(1): 116–121.
Zhou Jie, Wang Yalin, Luo Hong, et al. Study on performance of MIMO system with directional antenna elements[J].Journal of Huazhong University of Science and Technology (Natural Science Edition), 2015, 43(1): 116–121. |
| [12] |
周杰, 曹志钢, 菊池久和. 非对称空间统计信道模型及其MIMO多天线系统[J]. 东南大学学报:自然科学版, 2014, 44(2): 232–238.
Zhou Jie, Cao Zhigang, Kikuchi H. Asymmetric geometrical statistical channel model and MIMO wirelss communications[J].Journal of Southeast University:Natural Science Edition, 2014, 44(2): 232–238. |


