在假设用户均匀分布的场景中,联合优化小区范围扩展(CRE)和增强型小区间干扰协调(eICIC)不适用用户分布非均匀的实际场景.考虑到用户非均匀分布的特点,提出了相应的CRE和eICIC联合优化方案.考虑到建模的复杂性,使用了斯坦伯格博弈建模CRE和eICIC的联合优化过程,将宏基站作为领导者决定eICIC策略,将pico基站作为跟随者决定CRE策略,进而提出一种求解算法,以获得斯坦伯格博弈均衡解.仿真结果表明了所提出的斯坦伯格均衡解算法的收敛性及有效性.
As the effective methods to solve the load balance and interference control problem in heterogeneous cellular networks (HCN), cell range expansion (CRE) and enhanced inter-cell interference (eICIC) attract the attention of many researchers. However, most of the current works are under the assumption of uniform user distribution for simplicity, which is not applicable for the non-uniform user distribution scene. We intend to jointly optimize CRE and eICIC in HCN with non-uniform user distribution. Due to the complexity of the optimization problem, Stackelberg Game is used to model the optimization process of CRE and eICIC where macro base station (MBS) decides the eICIC strategy as leader and small cell base stations decide the respective CRE scheme as followers. Moreover, a solution algorithm is proposed to achieve the Stackelberg equilibrium (SE). The simulation results show the convergence of our proposed algorithm of SE and the effectiveness of our proposed solution.
异构蜂窝网络(HCN,heterogeneous cellular networks)在3GPP的LTE-A中,作为一种有效提升系统吞吐量的方案被广泛研究[1].其中一个热点问题是设计小区范围扩展(CRE, cell range expansion)以及增强型小区间干扰协调(eICIC,enhanced inter-cell interference coordination)[1-2].基于CRE和eICIC的异构蜂窝网络性能取决于范围扩展偏置因子(REB,range expansion bias)和几乎空白子帧(ABS,almost blank subframes)的配置.大量工作进行了相关研究[3-9],包括给定REB的情况下研究了ABS的配置问题[3],以及应用不同的方法联合优化CRE及eICIC来改善系统性能[4-8].然而现有研究在设计资源配置时统一假设用户为均匀分布,并未考虑用户分布特性的影响.因此,在假设用户分布非均匀的条件下,联合优化eICIC和CRE配置;考虑用户非均匀分布场景的复杂度,使用斯坦伯格博弈建模优化问题,并计算网络中最优的ABS密度及pico基站最优的REB配置.
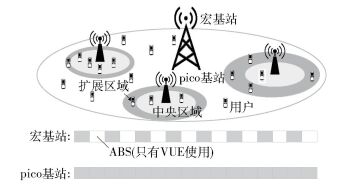
1 系统模型1.1 系统架构异构蜂窝网络架构如图 1所示,Npico个pico基站以频谱共享模式部署在一个宏基站(MBS,macro cellular base station)覆盖范围内,即pico基站及宏基站可以在相同频段同时传输.假设所有的pico基站发送功率相同,pico基站及MBS发送功率分别为Pp,Pm.系统用户数为N,连接到MBS的用户为Nm,连接第i个pico基站的用户数为Np, i.由于pico基站的小区范围扩展,pico基站用户分为易受干扰的用户(VUE,victim user equipments)及普通用户类型,且为两个互补子集合,分别表示为Np, iv和Np, in. Np, iv的值取决于偏置值bi及用户分布密度ρi. ABS密度表示为α. pico基站在没有宏蜂窝干扰的情况下使用ABS给VUE发送数据.剩余的子帧供宏蜂窝用户(MUE, macro user equipments)及pico基站普通用户使用.分别定义umj,up, ij,
|
图 1 网络架构 |
对于MUE umj,受到来自所有pico基站的干扰,其信干噪比表示为

|
(1) |
其中:hij为基站i到用户j间的平均信道增益,σ2为噪声功率.同理,pico基站的普通用户受到来自MBS和其他pico基站的干扰,其信干噪比表示为

|
(2) |
pico基站中VUE使用ABS消除干扰,所以仅受到来自其他pico基站的干扰,其信干噪比表示为
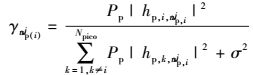
|
(3) |
由香农公式可得用户的传输速率

|
(4) |
为了最大化异构蜂窝网络系统吞吐量,实现负载均衡,因此联合设计最优的eICIC和CRE方案.进而需要得到1) 最优的ABS密度α;2) 每个pico基站对应的最优的REB值,即β=[β1, β2, …, βNpico].
为了改善系统吞吐量,MBS将服务质量低的用户VUE分给pico基站从而减轻负载;同时,为了鼓励pico基站扩展覆盖范围实现分流,MBS通过增加ABS密度α作为对pico基站的回报.该过程可以建模为斯坦伯格博弈.斯坦伯格博弈是一个策略博弈,包括一个领导者及多个跟随者互相竞争资源.建模MBS为领导者,pico基站为跟随者. MBS根据效用函数给出一个ABS密度值α. pico基站根据MBS的决策及效用函数计算REB值β,并且假设所有的pico基站理性且自私,其目标是最大化各自的效用函数.
由于MBS及pico基站的同频部署,临近pico基站的MUE受到严重的跨层干扰,极大地降低了系统性能,通过将信道条件差的用户分配到pico基站,系统平均吞吐量增加,并且为MBS分流.因此,定义所有用户平均吞吐量为MBS效用函数.具体表示为
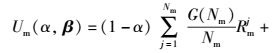
|
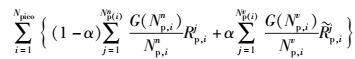
|
(5) |
其中,G函数表示多用户分集增益,可以表示为[9]

|
(6) |
Nm取决于向量β,βi的值越大表示更多的MUE被分配到第i个pico基站,MUE数量较少.另外,在斯坦伯格博弈中,对∀i,βi是关于α的增函数;因为仅当ABS密度增加时,pico基站才愿意接纳更多的VUE并提供更好的服务,进而表明pico基站的小区范围扩展取决于ABS密度.然而,当过分增大ABS密度时,MUE可用资源减少,导致MBS效用函数下降.因此,MBS必须确定最优的ABS密度值最大化效用函数,具体通过解决以下问题实现.
问题1:

|
(7) |
同理,在pico基站侧,定义其效用函数为
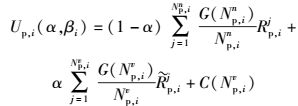
|
(8) |
为了鼓励pico基站扩展小区范围,定义C函数为激励函数,且C函数关于Np, iv为递增的凸函数,表示为
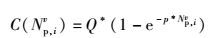
|
(9) |
其中Q和p是常数.
由式(8) 可知,对于pico基站改善REB的回报主要体现在两方面:一是ABS密度的增加带来平均吞吐量的收益;二是激励函数的收益.固定ABS密度的条件下,当pico增加扩展偏置数值时,更多的MUE分配到pico基站,其回报将会增加.然而,随着偏置数值增加,过多的MUE接入到pico基站,由于通信距离增加及干扰,VUE的信道质量降低,导致VUE的平均吞吐量下降.因此,有必要选择最优的CRE偏置因子,最大化pico基站的效用函数.其问题建模为
问题2:
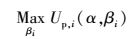
|
(10) |
问题1与问题2联合构成了斯坦伯格博弈.博弈的目标是找到斯坦伯格博弈均衡解(SE,Stackelberg equilibrium),从而保证领导者(MBS)及跟随者(pico基站)无法单方面脱离SE.
2 问题求解2.1 算法设计对于上述斯坦纳伯格博弈,SE定义如下:取α*为问题1的一个可行解,βi*为问题2的一个可行解,当满足如下条件时,对于所有的可行解(α, β),(α*, β*)是斯坦伯格博弈的SE.
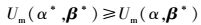
|
(11) |

|
(12) |
为了求得SE,使用倒推法分析斯坦伯格博弈:领导者(MBS)首先变化,跟随者(pico基站)相应做出变化.首先,MBS决定一个ABS密度α的策略,下一步每个pico基站调整偏置因子βi,决定扩展范围并优化效用函数.
对于一个给定的ABS密度α,通过求解问题2,每个pico基站选择一个最优的REB.由于Np, in是离散的,导致函数Up, i非线性.因此,不能得到βi的闭式解.但是,由于MBS接入的用户数量是固定的,且REB最大值为15 dB[10],pico基站通过研究所有可能的策略,可以发现最优的βi.令βi*表示问题2的最优解.即
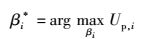
|
(13) |
由于MBS通过X2接口得知pico基站的情况.基于所有pico基站的最佳响应β*=[β1*, β2*, …, β*Np],从而MBS确定ABS密度α.策略α通过求解问题1最大化效用函数来得到.
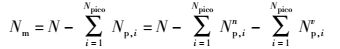
|
(14) |
式(14) 表示pico基站小区扩展之后的MUE数量.除了变量α外其他变量均已知,容易求得变量α的值.表示问题1的最优α值为α*.则MBS的最优策略表示为

|
(15) |
在获得α*后,pico基站根据α*值继续调整REB获得最优的β*,继而MBS继续依据β*,重新计算新的α*.在一定时间范围内,直到MBS和pico基站的效用函数不再增加时,博弈结束.
2.2 算法步骤SE求解算法步骤
步骤1 MBS根据历史信息寻找一个确定的α值.
步骤2 迭代
while(Um值增加)
初始化β=[0, …, 0]
while(Up, i值增加)
βi=βi+δ
更新Up, i
end while
根据α得到最优的β*
根据β*得到Um
计算当下最优值α
end while
步骤3 得到最优的α*和β*.
3 仿真结果在仿真部分,所有系统参数及假设均参考LTE标准[10]. 表 1总结了重要的仿真参数,采用文献[10]中郊区部署下的路径损耗模型.所有pico基站可以选择各自最优的REB,而非同一个数值,更符合场景中用户非均匀分布的特点.
|
|
表 1 关键仿真参数 |
图 2仿真了一个pico基站在不同的ABS密度中的效用函数值.如图 2所示,起初pico基站的效用值随着REB增加而增加,后随着REB的进一步增加而下降.并且α的值越大,效用函数值也越大. pico基站效用函数最大值随着α增加而增加.该结果可以理解为:pico基站基于偏置因子扩展小区范围,更多的MUE成为VUE,激励函数的存在使pico基站的效用函数增加.然而,如果太多用户接入pico基站,导致更多的VUE信道条件变差,降低了pico基站的性能.而ABS密度α增大,VUE可以使用更多的ABS资源,因此,pico基站效用值更好,且最大值变慢.

|
图 2 不同α和β值下的pico基站效用值 |
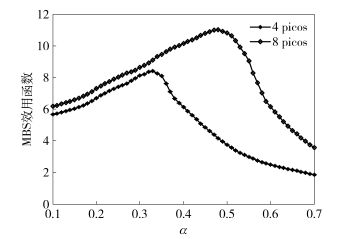
图 3揭示了MBS的效用值与α及pico基站数量的关系.当α值较低时提高α值,导致pico基站增加REB,进而临近pico基站的MUE接入pico基站.然而,当α过分增大时,MBS的效用值下降.由分析知剩余的非ABS密度太低,不能满足MUE的需求.另外,可以看出在不同pico基站数量下的最优值α*不同,8基站的α*大于4基站的α*,因为当MUE数量较多时,pico基站越多时,可以接入MUE的数量越多,作为回报MBS释放更多的时隙资源.
|
图 3 不同pico基站数量和α值的MBS效用值 |
图 4表明了SE求解算法的收敛性.设定4个pico基站用户密度逐渐增加,如图所示,MBS及所有pico基站在120 ms之后达到收敛,并且得到α=0.32,β=[3, 5, 8, 10].在仿真中,MBS每10 ms调整一次α值,pico基站相应地从0开始调整β,导致pico基站的非线性增长.另外,用户密度高的pico基站的效用值及最优REB值胜于用户密度低的pico基站.因为用户分布密度高的平均信道质量更好.

|
图 4 MBS和pico基站效用函数的收敛性 |
研究了在用户非均匀分布的异构蜂窝网络中,联合优化CRE及eICIC的问题.通过分析在CRE中的参数REB及eICIC中的参数ABS密度,构建了斯坦伯格博弈的联合优化问题,并且在博弈中,MBS作为领导者决定ABS密度,pico基站作为跟随者决定REB.另外,提出了迭代的求解算法获得SE.最终,仿真结果表明了提出的SE算法的有效性,并验证了针对用户非均匀分布场景下联合优化CRE及eICIC方案性能的优越性.
| [1] | Pedersen K I, Wang Y, Strzyz S, et al. Enhanced inter-cell interference coordination in co-channel multi-layer LTE-advanced networks[J].IEEE Wireless Communications, 2013, 20(3): 120–127. doi: 10.1109/MWC.2013.6549291 |
| [2] | Pang Jiyong, Wang Jun, Wang Dongyao, et al. Optimized time-domain resource partitioning for enhanced Inter-cell interference coordination in heterogeneous networks[C]//2012 IEEE Wireless Communications & Networking Conference (WCNC2012). Shanghai:IEEE Press, 2012:1613-1617. |
| [3] | Singh S, Andrews J G. Joint resource partitioning and offloading in heterogeneous cellular networks[J].IEEE Transactions on Wireless Communications, 2014, 13(2): 888–901. doi: 10.1109/TWC.2013.120713.130548 |
| [4] | Yamamoto K, Ohtsuki T. Parameter optimization using local search for CRE and eICIC in heterogeneous network[C]//2014 IEEE 25th Annual International Symposium on Personal, Indoor, and Mobile Radio Communication. Washington DC:IEEE Press, 2014:1536-1540. |
| [5] | Deb S, Monogioudis P, Miernik J. Algorithms for enhanced inter-cell interference coordination (eICIC) in LTE HetNets[J].IEEE/ACM Transactions on Networking, 2014, 22(1): 137–150. doi: 10.1109/TNET.2013.2246820 |
| [6] | Zhou Hao, Ji Yusheng, Wang Xiaoyan. ADMM based algorithm for eICIC configuration in heterogeneous cellular networks[C]//2015 IEEE Conference on Computer Communications. Kowloon:IEEE Press, 2015:343-351. |
| [7] | Grøndalen O, Mahmood K, Østerbø O N. On attachment optimization and muting pattern selection in eICIC[C]//2016 IEEE 27th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications. Valencia:IEEE Press, 2016:1-6. |
| [8] | Zhou Hao, Ji Yusheng, Wang Xiaoyan, et al. eICIC configuration algorithm with service scalability in heterogeneous cellular networks[J].IEEE/ACM Transactions on Networking, 2017, 25(1): 520–535. doi: 10.1109/TNET.2016.2588507 |
| [9] | Bu T, Li L, Ramjee R. Generalized proportional fair scheduling in third generation wireless data networks[C]//25th IEEE International Conference on Computer Communications. Barcelona:IEEE Press, 2006:1-12. |
| [10] | 3GPP TSG RAN WG4. R4-092042-2009, Simulation assumptions and parameters for FDD HeNB RF requirements[S]. San Francisco:Alcatel-Lucent, picoCHip Designs, Vodafone, 2009. |



