为了实现多项式数据通路的高层次综合,采用有序、简化和正则的带权值广义表模型表达该多项式。首先对该带权值广义表进行线性化处理;然后提出了基于带权值广义表的多项式数据通路的高层次优化方法。该方法以自底向上的方式遍历带权值广义表中的节点,并迭代地析取该带权值广义表中的乘法和加法项,进而将该带权值广义表转换为不可简化的有层次的带权值广义表集合,最终将该集合转换为更适于高层次综合的可调度数据流图。实验结果表明,与传统的方法相比,采用该方法得到的数据流图转化为寄存器传输级结构具有更小的延迟和面积。
In order to implement high level synthesis for polynomial datapaths, the ordered, reduced and canonical weighted generalized list was used to represent for the polynomials. The weighted generalized list was linearized firstly. And based on the weighted generalized list, a high level optimization method for polynomial datapaths was given, which traverses the nodes of the weighted generalized list in a bottom-up fashion and extracted the product terms and sum terms from the weighted generalized list iteratively, and then transformes weighted generalized list into a set of irreducible hierarchical weighted generalized lists, and finally transformes the set of irreducible hierarchical weighted generalized lists into corresponding schedulable data flow graphs which are better suited for high level synthesis. Experiments show that the register transfer level structure which obtained from the schedulable data flow graphs generated by the proposed method had smaller latency and less datapth area than those obtained using traditional methods.
算术密集型设计的初始化设计规范往往可以抽象成多项式描述[1],对该设计的高层次综合,需要采用有效的方法对初始的算术规范进行优化.而传统的优化方法包括:基本代数性质的方法[2-5]、基于多项式符号代数的方法[6]、基于因子分解和公共子表达消去方法[1, 7],均没有提供一种正则的表达方式对相应的多项式进行描述,严重缩小了优化的范围.由于带权值广义表[8](WGL,weighted generalized list) 可有效地表达多项式,笔者提出一种基于WGL的方法来实现初始设计规范的优化.通过对WGL进行线性化处理,然后迭代地对该线性WGL进行分解,最终可产生适用于高级综合的优化数据流图 (DFG,data flow graph).采用传统的综合工具可将该DFG综合成时延和面积更优化的硬件实现.
1 WGL表达多项式对于多元整系数多项式f(x0, x1, …, xn-1),变量x0在x0=0时的泰勒展开结果为
| $ \begin{array}{*{20}{c}} {f\left( {{x_0},{x_1}, \cdots ,{x_{n - 1}}} \right) = f\left( {0,{x_1}, \cdots ,{x_{n - 1}}} \right) + }\\ {{x_0}\frac{\partial }{{\partial {x_0}}}f\left( {0,{x_1}, \cdots ,{x_{n - 1}}} \right) + }\\ {\frac{{x_0^2}}{{2!}}\frac{{{\partial ^2}}}{{\partial x_0^2}}f\left( {0,{x_1}, \cdots ,{x_{n - 1}}} \right) + \cdots + }\\ {\frac{{x_0^i}}{{i!}}\frac{{{\partial ^i}}}{{\partial x_0^i}}f\left( {0,{x_1}, \cdots ,{x_{n - 1}}} \right) + \cdots } \end{array} $ | (1) |
其中:
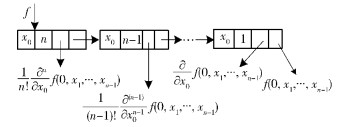
式 (1) 中的其他变量按一定的顺序并按同样的方法迭代地进行泰勒展开,其结果可采用如图 1所示的WGL表示.其中,WGL的节点表达泰勒展开的单个项,且WGL的每个节点用分解变量的名字标记.每条边用w标记,其中w为边的权.可对WGL进行简化和标准化操作[8],对于一个固定变量顺序、简化、标准化的WGL是正则的.
|
图 1 WGL分解规则 |
定理1[8] 对于任意整系数多项式f(x0, x1, …, xn-1),存在一个唯一、有序、简化的WGL表达f(x0, x1, …, xn-1),且任何其他与该WGL有相同变量顺序的WGL表达f(x0, x1, …, xn-1) 会包含更多的节点.换言之,一个有序、简化WGL是最小的和正则的.
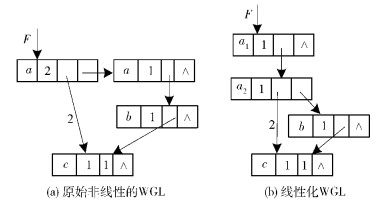
对于线性多元多项式的因式分解,采用WGL的结构是有效的.例如,WGL表达变量顺序为 (a, b, c) 的多项式F=ab+ac,可表达为因子分解形式F=a(b+c).然而,当涉及非线性表达时,WGL表达就失去其有效性.例如,WGL表达多项式F=2a2c+abc,如图 2(a)所示,节点a应该继续因子分解,形成更紧凑的形式F=a(2a+b)c,但图 2(a)所示的WGL不允许这样的因子分解.不过可将其转换为线性形式,并支持因子分解.对于xk(k>1),可将其转化为xk=x1x2…xk,其中∀i, j,xi=xj.如式 (2) 所示的非线性表达.把每次出现的xk替换为x1x2…xk,可将其转换为线性表达,形成如式 (3) 所示的Horner型. Horner型的特点为包含的乘法数最少,因此适合于最少硬件资源数的实现.
|
图 2 WGL表达F=2a2c+abc |
| $ F\left( x \right) = {f_0} + x{f_1} + {x^2}{f_2} + \cdots + {x^n}{f_n} $ | (2) |
| $ F\left( x \right) = {f_0} + {x_1}\left( {{f_1} + {x_2}\left( {{f_2} + \cdots + {x_n}{f_n}} \right)} \right) $ | (3) |
通过该规则,函数F=2a2c+abc可看作为F=2a1a2c+a1bc,可简化为F=a1(2a2+b)c,等价于F=a(2a+b)c,如图 2(b)所示. WGL的线性化可通过迭代把高次方节点分裂,直到每个节点表达变量的次方为1.
引理1 对一个有序、简化的WGL进行线性化,得到的线性WGL是唯一、正则和最小的.
证明 唯一性.一个有序、简化的线性WGL是由有序、简化的WGL通过线性化得到的,根据定理1可知有序、简化的WGL是唯一的,那么相应的线性WGL中无冗余的节点,同时该线性WGL中不包含任何同构的子表,因此一个有序、简化的线性WGL中的所有节点是唯一的.
正则性.由于一个有序、简化的WGL是正则的,那么该WGL进行线性化后每个节点对应的分解是唯一的,因此该WGL进行线性化后得到相应的线性WGL是正则的.
最小性.若L为一个有序、简化、正则的WGL通过线性化后得到的线性WGL,假设存在另一个线性WGL,L′也是由该WGL通过线性化后得到的,且L′的节点数比L少,那么,说明L还可通过简化操作简化为L′.然而由于L是正则的线性WGL,且不包含冗余的节点,那么,L′的节点数不可能比L少,因此L是最小的和正则的.
下面提到的WGL都为线性的WGL.
2 迭代的WGL分解代数分解的主要目标是使表达中代数运算 (加法和乘法) 数最少.例如,F=ab+ac可通过因子分解转化为F=a(b+c),并把乘法数量由2减少到1.同时,若代数表达中的某个子表达在该代数表达中出现超过1次,那么可析取该子表达,并用新的变量来替换它,该过程称之为公共子表达消去.通过因式分解和公共子表达消去把某个代数表达化简的方式称之为分解.
笔者利用WGL紧凑的正则表达,在WGL上直接进行代数分解,通过析取一些简单的项,并用新的变量来替换这些项,然后在更高层次图上按照同样的方式进行分解.分解的最终结果为一系列层次的不可简化的WGL.分解算法以式 (4) 为例进行说明为
| $ F = def + dg + ijl + dhl + kl $ | (4) |
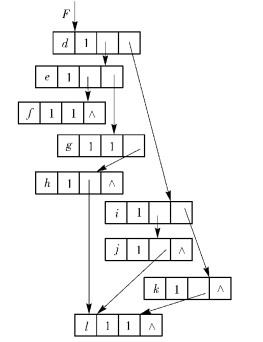
其中包含8个乘法和4个加法.通过执行WGL分解可把该表达进行简化,并得到1个含有较少乘法运算的DFG. 图 3所示为式 (4) 的WGL表达.
|
图 3 WGL表达F=def+dg+ijl+dhl+kl |
可析取积项为WGL中变量的积,即∏xi,且该积在WGL中仅出现1次.积项析取的主要任务是识别仅由一系列乘法边相连的WGL节点的子集,该子集中的中间节点仅有1条父亲边和1条孩子边,且这2条边必须为乘法边,只有子集中的开始和结束节点有其他的加法边.然后,采用单个WGL节点来替换每个这样的子集,且它的功能由新的变量Pi表达.具体的积项析取算法如算法1所示.
算法1 积项析取,在WGL中化简所有的积项,并把这些积项添加到不可简化的WGL列表.
Procedure ProductTerm (){
result=false;
LV=WGL中自底向上出现变量的列表;
while (LV≠∅){
lvf=LV的头节点;
LV=LV-{lvf};
LPT=∅; (积项节点的列表)
LPT=LPT∪{lvf };
if (∃!节点lvf的乘法父节点p) then{
LPT=LPT∪{p};
while (p≠∅){
if (∃!节点p的乘法父节点k,且节点k不存在加法子节点) then{
p=k;
LPT=LPT∪{p};
productFount=true;
} else
p=∅;
}
If productFount then{
产生变量Vi;
产生积项Ti=∏n∈LPT;
LEW=LEW∪{Ti}; (不可简化的WGL列表)
用Vi替换Ti;
result=true;
}
}
}
return result;
}
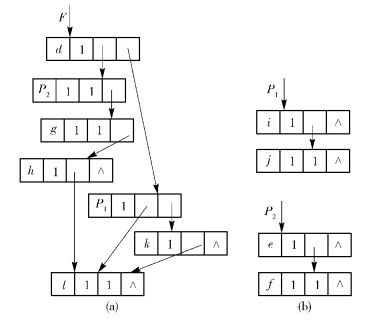
由算法1可知,以自底向上的方式遍历WGL,对于每个节点按照深度优先的方式遍历所有与它相连的节点,如果这些节点满足积项的条件,就把这些节点列入积项节点的列表中.如图 3所示的WGL,从终节点开始首先访问节点l.该节点有多个扇入乘法边,因此不能构造积项,接着访问节点j,由于节点j仅有乘法父节点i,且节点i只有加法父节点,所以产生了一个可析取积项ij,并把该积项加入到列表LEW中;然后用变量P1替换积项ij,并在WGL中对相应的节点进行替换.按照同样的方法,在图 3中还可析取积项ef,并用变量P2替换,如图 4所示,其中图 4(a)为简化的WGL,节点P1和P2分别替换积项ij和ef.由于积项kl、jl和hl的析取需要重复的节点l,所以这些项不是可析取积项.
|
图 4 对图 3WGL进行积项析取的结果 |
可析取和项为WGL中变量的和,即∑xi.与可析取积项相似,WGL中和项以节点集出现,该节点集中所有节点的乘法边连接1个公共节点或未连接任何节点,且这些节点由加法边相连.具体的和项析取算法如算法2所示.
算法2 和项析取,化简WGL中的和项并把这些和项添加到不可约WGL列表中
Procedure SumTerm (){
result=false;
LV=WGL中自底向上出现的变量列表;
while (LV≠∅) {
lvf=LV的头节点;
LV=LV-{lvf};
if (∃节点lvf的乘法父节点) then
LP=节点lvf的乘法父节点列表;
else
LP={lvf}∪节点中无乘法边的节点列表;
sumFound=false;
while (LP≠∅) {
LST=∅;(和项节点的列表)
lpf=LP的头节点;
LP=LP-{lpf};
LST=LST∪{lpf};
for (每个节点p∈LP){
if (p∈LP的加法边存在) then{
LST=LST∪{p};
sumFound=true;
}
}
if sumFound then{
产生变量Vi;
产生Ti=∑n∈LST;
LET=LET∪{Ti};
用变量Vi替换Ti;
result=true;
}
}
}
return result;
}
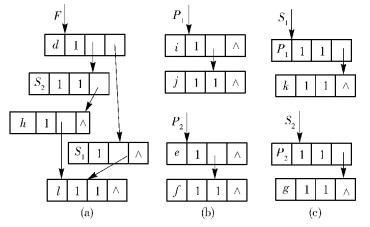
由算法2可知,通过自底向上的方式遍历该WGL,且对于每个节点v,存在2种情况:1) 若存在多个节点的乘法边都连接节点v,且这些节点都以加法边相连接,那么把这些节点加入到可析取和项的列表中;2) 若不存在节点的乘法边与节点v相连接,则把WGL中所有无乘法边相连的节点找出,然后再验证这些节点是否由加法边相连,进而析取相应的和项.如图 4(a)所示,从节点l开始的可达节点的列表为{h, P1, k},其中{k, P1}由加法边连接.因此,形成一个加法项 (P1+k).用新的变量S1替换该和项,并把该和项表达为一个不可简化的WGL;由算法2可知,在图 4(a)中还可析取和项 (P2+g),并用变量S2替换.直到从简化的WGL中不能再析取出其他的和项,最终得到层次化的WGL集合,如图 5所示,其中图 5(a)为顶层的WGL.如果WGL中没有和项,那么应用算法1描述的积项析取后可能会得到额外的和项,例如图 3中没有和项,然而析取积项后,包含和项S1=P1+k和S2=P2+g,如图 4所示.
|
图 5 对图 4WGL进行和项析取的结果 |
迭代地进行积项和和项析取,最终形成的顶层WGL是不可简化的,即采用算法1和算法2不能将该WGL进一步化简,如图 5(a)所示的顶层WGL.从该WGL根节点开始,按照一定的拓扑顺序遍历该WGL.根据泰勒分解规则,访问节点xi,相应的表达F(xi) 为
| $ F\left( {{x_i}} \right) = {x_i}{F_1}\left( {{x_{i + 1}}} \right) + {F_0}\left( {{x_{i + 1}}} \right) $ | (5) |
其中:F0(xi+1) 为从节点xi开始的由加法边相连的子WGL,F1(xi+1) 为从节点xi开始的由乘法边相连的子WGL.
如图 5(a)相应的表达式为
| $ F = d\left( {{S_2} + hl} \right) + {S_1}l $ | (6) |
其中:和项S1=P1+k和S2=P2+g以及积项P1=ij和P2=ef均为不可简化的WGL.
迭代地执行WGL分解最终会产生一种简化的因式形式的代数表达,通过对表达中的变量顺序实施附加规则,得到的表达形式是唯一的.
定义 如果因式形式表达中的变量顺序与WGL中的变量顺序一致,那么该因式形式表达称为WGL的标准因式形式.
式 (6) 中变量出现的顺序与顶层WGL中的变量顺序一致.由于d为WGL中的第1个变量,所以项d(S2+hl) 首先出现,接着项S1l位于较下面的位置.同样,项 (S2+hl) 中的变量顺序与WGL中的变量顺序一致,因此子表达P1、P2和S1、S2中的变量顺序与积项和和项的析取相关.
定理2 从线性WGL中得到的标准因式形式是唯一的.
证明 标准因式形式迭代的定义为代数表达的积之和或和之积.在最低层的分解中,积项 (和项) 为变量的乘积 (变量的和),其中每个变量仅出现1次,且该变量的顺序是与WGL中的变量顺序一致.因此,描述该项的表达是唯一的.随后WGL的积项或和项析取相对应新的表达会产生新的变量.根据WGL的正则性,每个这样的变量是唯一的,且在当前WGL中的位置也是唯一的,因此相对应的表达也是唯一的.所以,对于任何分解点,每个子表达是唯一的,最终的标准因式形式表达也是唯一的.
3 数据流图的构建一旦WGL被分解,并产生相应的标准因式形式,那么就可构建该表达相应的DFG.首先,采用标准因式形式的基本性质是把每个不可简化的WGL转化成1个简单的DFG,即将WGL中的每条加法边和每条乘法边分别映射为DFG中相应的加法运算和乘法运算,DFG的每个节点仅有2条扇入边,分别连接的是相关运算的2个操作数.在构建DFG的过程中,将DFG的每个节点存储在哈希表中,并以相应的WGL函数为键值.在构建DFG的任一节点时,如果相应DFG节点的表达在该哈希表中,那么需要重用该表达.例如,当构建节点f=abc时,首先构建子表达节点z=ab,接着构建节点f=zc.如果子表达节点z=ab已经构建,那么节点f=zc可重用该子表达.这从DFG中消除了潜在的冗余,且该冗余无法通过因子分解而捕获到.
图 6所示的DFG是从图 5所示WGL的分解中得到.与标准因式形式不同,DFG表达是不唯一的.当运算数保持一定时,可采用逻辑综合和高级综合的方法将DFG进一步的重建并平衡最小延迟.
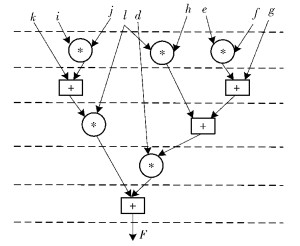
|
图 6 从图 5中得到的DFG |
笔者针对滤波器和计算机图形算法来测试提出算法的有效性,分别对5次样条函数、4次样条函数、Savitzky-Golay滤波器和余弦小波计算进行了实验.首先,通过高级综合系统GAUT将采用C语言所写的设计进行编译,产生一个初始的DFG;然后,根据李东海等[8]提供的方法将该DFG转换为WGL;接着采用笔者的方法将该WGL进行分解,产生优化的DFG;最后,采用高级综合系统GAUT将优化的DFG转化为寄存器传输级 (RTL,register transfer level) 结构. 表 1分别为采用原始设计和笔者算法得到的DFG的结果,其中移位运算为常系数乘法的变换.
|
|
表 1 用GAUT和笔者算法得到的DFG结果 |
同时给定延迟约束,对DFG进行重新调度得到所需的实际资源数,结果如表 2所示.表中延迟参数如下:乘法器为18 ns;加法器为8 ns;移位运算为9 ns;时钟周期为10 ns;面积为GAUT给出的虚拟单元.对于给定延迟不能进行综合的标记为“-”.对于5次样条函数,原始设计得到的最小延迟为180 ns,用笔者算法得到的最小延迟为110 ns;对于4次样条函数,原始设计得到的最小延迟为160 ns,用笔者算法得到的最小延迟为100 ns;对于Savitzky-Golay滤波器,原始设计得到的最小延迟为160 ns,用笔者算法得到的最小延迟为120 ns;余弦小波计算原始设计得到的最小延迟为180 ns,用笔者算法得到的最小延迟为110 ns.同时在相同的延迟下,笔者算法得到的面积比原始设计小.
|
|
表 2 用GAUT和笔者算法得到DFG在延迟约束下进行重新调度的结果 |
基于WGL分解,实现了一种把初始算术规范转换为优化的DFG的方法,该方法适合于算术密集型的高层次综合.由实验结果可知,该方法得到的DFG与传统的方法相比能找到更低延迟的RTL实现;同时,在相同的延迟下,采用该方法能得到更少运算数的RTL实现.
| [1] | Ghandali S, Alizadeh B, Fujita M, et al. Automatic high-level data-flow synthesis and optimization of polynomial datapaths using functional decomposition[J]. IEEE Trans on Comput, 2015, 64(6): 1579–1593. |
| [2] | Gupta S, Savoiu N, Dutt N, et al. Using global code motion to improve the quality of results in high level synthesis[J]. IEEE Trans on Comput Aided Des Integr Circuits Syst, 2004, 23(2): 302–312. doi: 10.1109/TCAD.2003.822105 |
| [3] | Mantovani P, Guglielmo G D, Carloni P L. High-level synthesis of accelerators in embedded scalable platforms[C]//ASP-DAC 2016. Macao:China, 2016:204-211. |
| [4] | Sierra R, Carreras C, Caffarena G. A formal method for optimal high-level casting of heterogeneous fixed-point adders and subtractors[J]. IEEE Trans on Comput Aided Des Integr Circuits Syst, 2015, 34(1): 52–62. doi: 10.1109/TCAD.2014.2365094 |
| [5] | Zheng Hongbin, Gurumani S T, Yang Liwei, et al. High-level synthesis with behavioral-level multicycle path analysis[J]. IEEE Trans on Comput Aided Des Integr Circuits Syst, 2014, 33(12): 1832–1845. doi: 10.1109/TCAD.2014.2361661 |
| [6] | Peymandoust A, Micheli G D. Application of symbolic computer algebra in high-level data-flow synthesis[J]. IEEE Trans on Comput Aided Des Integr Circuits Syst, 2003, 22(9): 1154–1165. doi: 10.1109/TCAD.2003.816213 |
| [7] | Ghandali S, Alizadeh B, Fujita M, et al. RTL datapath optimization using system-level transformations[C]//ISQED 2014. Santa Clara:CA, 2014:309-316. |
| [8] |
李东海, 马光胜, 胡靖. 高层次数据通路的等价性验证方法[J]. 哈尔滨工程大学学报, 2008, 29(6): 583–588.
Li Donghai, Ma Guangsheng, Hu Jing. The method of equivalence verification for high level datapaths[J]. Journal of Harbin Engineering University, 2008, 29(6): 583–588. |


