在滚动轴承进行故障识别中,针对局部均值分解(LMD)方法分析非平稳、非线性含噪信号时,存在端点效应,易产生虚假分量和单通道独立成分分析(ICA)盲源分离时的欠定问题,提出了基于LMD-ICA降噪的振动信号特征提取算法。首先对原始信号进行LMD,并抑制端点效应,得到n个瞬时频率具有物理意义的乘积函数(PF)之和;然后对得到的PF分量以连续的3阶PF分量为一序列组合进行ICA,可以得到n-2个重构分量;最后利用n-2个分量进行重构,得到降噪后的故障信号,并再次进行LMD或功率谱计算,提取故障特征。经验证,该方法可有效识别滚动轴承的多类故障。
Aiming at the problem of existing the end effect, easily producing false component. The local mean decomposition (LMD) was used in analysis of non-stationary and nonlinear signals containing noise and the underdetermined problem of the single channel independent component analysis (ICA) blind source separation, the feature extraction algorithm of the vibration signals based on the noise reduction LMD-ICA was proposed. By applying the algorithm, the fault of rolling bearing is diagnosed, firstly, the original signals are decomposed by LMD, the n instantaneous frequency product function (PF) components with physical significance are obtained and the end effect is limited. Then the obtained PF components which are arranged into one sequence combination per constant third-order PF components are analyzed by independent component. And n-2 refactoring components can be obtained by ICA. At last, the fault signals of which the noises are reduced are decomposed by LMD or calculated by power spectrum again to extract the fault. According to the experiment, the multi-types fault signals of rolling bearing can be effectively recognized by the method proposed above.
滚动轴承在各种机械传动中应用广泛,它工作状况的优劣程度将影响旋转机械的运行,旋转机械中滚动轴承发生故障的概率很高,大约有30%的故障都是由滚动轴承引起的,因此,对滚动轴承运行状态的检测及故障诊断意义重大[1-2].然而故障信号往往混杂在环境噪声中,使得故障特征提取变得复杂.针对各类滚动轴承故障信号的非线性、非平稳性,局部均值分解 (LMD,local mean decomposition) 存在虚假乘积函数 (PF, product function) 分量及单通道独立成分分析 (ICA, independent component analysis) 盲源分离的欠定问题,提出先对故障信号整体降噪,再进行LMD与故障特征提取的基于LMD-ICA降噪的振动信号特征提取算法.
1 原理和方法 1.1 LMD及其端点效应 1.1.1 LMDLMD的实质是将振动信号分解为许多PF分量之和,每个分量都是单频信号,都是由一个包络信号和一个纯调频信号通过乘积运算得到,故一个含有多分量的振动信号经LMD可表示为一系列具有物理意义的单分量和的形式[3].对于给定的振动信号x(t),其分解流程如图 1所示.图中,x(t) 为原始振动信号,sij(t)、uj(t) 为中间变量,mij(t)、Aij(t) 分别为局域均值函数和包络估计函数,ai(t) 为包络信号,为LMD分量.

|
图 1 LMD流程 |
LMD在进行振动信号分析时,其端点效应会由端点逐渐向内扩散,致使LMD时产生虚假分量[4],该虚假分量将为ICA提供虚假观测分量.因此,必须进一步抑制LMD的端点效应.
1.1.2 端点效应解决方法目前对于LMD端点效应的处理方法有很多,均取得了一定效果,但也存在一定的局限性.例如,极值点延拓[5]要求信号本身对称性较强,对短序列信号处理效果一般,没有顾及信号内部规律;边界波形匹配预测法[6]抑制端点效应时虽顾及了信号内部规律,但自适应性较差,对边界点处发生突变的信号效果较差;神经网络法[7]、自回归滑动平均模型[8]等预测类延拓法对端点效应的抑制效果依赖于预测工具本身的参数设置,且训练样本多,学习时间长.针对以上多种端点效应抑制方法存在的问题,提出采用自适应波形匹配法来抑制LMD的端点效应,下面以左端点延拓来说明该方法.
1) 找出原始信号x(t) 的非极值左端点m、极大值点mi和极小值点ni(i=1, 2, …, n),对应时间分别为tm、tmi、tni,过点m做平行于X轴的直线交x(t) 于pi,时间为ti,取tm~t2间的长度为L.
2) 以曲线m-m1-n1-p2为特征曲线,以步长L为单位向右平移,逐个寻找匹配曲线;计算特征波形与所有匹配波形的误差,误差计算公式为
| $ {e_i} = \left| {{p_{2i}} - m} \right| + \left| {{m_i} - {m_1}} \right| + \left| {{n_i} - {n_1}} \right| + \left| {{p_{2\left( {i + 1} \right)}} - {p_2}} \right| $ | (1) |
3) 比较各误差值,找出一个最小的ei,以此段波形为匹配波形,取匹配波形的左端作为x(t) 的左端延拓波形.按照同样的方法进行右端延拓,可得到完整的波形曲线.
1.2 ICAICA可以从多元或多维统计数据中寻找其内在的独立成分[5],ICA的一般线性模型为
| $ \mathit{\boldsymbol{X}}\left( t \right) = \mathit{\boldsymbol{AS}}\left( t \right) $ | (2) |
其中:X(t) 为观测的n维随机向量,S(t) 为n维独立的源信号向量,A为n×n的混合矩阵.
ICA的目的就是在源信号向量S(t) 和混合矩阵A未知的情况下[5]求解混合矩阵A和源信号的最优解Y,即
| $ \mathit{\boldsymbol{Y}} = \mathit{\boldsymbol{WX}} $ | (3) |
其中: W为混合矩阵A的逆矩阵,Y是源信号的近似逼近. ICA模型求解有多种方法,笔者采用鲁棒性好、收敛快的基于负熵的快速收敛算法.
1.3 LMD-ICA的提出ICA在信号处理时,要求信号具有全面性,因此,信号采集时存在传感器的数目大于或等于源信号的局限. LMD对噪声很敏感,噪声信号的干扰将导致LMD效果不明显.因此,提出LMD-ICA降噪的故障信号特征提取算法,先整体降噪,降噪后再对信号LMD提取故障特征.
2 LMD-ICA信号降噪和特征提取研究 2.1 基于LMD-ICA的降噪与故障信号特征提取方法基于LMD-ICA的降噪与故障信号特征提取流程如图 2所示,经过LMD-ICA联合技术降噪后再对故障信号进行特征提取可提高滚动轴承故障诊断的准确性,其实现方法如下.
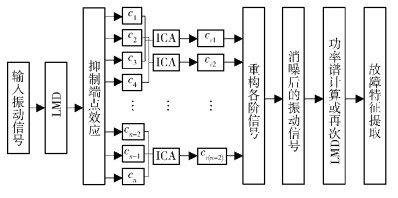
|
图 2 基于LMD-ICA方法的故障信号降噪流程 |
1) 用LMD算法求解故障信号的各阶PF分量,得到信号的n个PF (c1, c2, …, cn) 分量;用自适应波形匹配法进行端点延拓,抑制LMD的端点效应.
2) 由于LMD对噪声敏感,分解后仍存在虚假PF分量,提出了以特征最为相似的连续3阶PF分量为一组进行ICA,较其他2个分量不同的噪声分量就可被剔除.例如,取前3阶PF进行ICA,选取最优的分析结果作为重构信号的第1个重构分量cr1;再取2、3、4阶PF进行ICA,得到重构信号的第2个重构分量cr2,以此类推,得到重构信号的第n-2个重构分量.
3) 经ICA可以得到n-2个重构分量,这n-2个重构分量的重构信号和原始信号最为接近,所以利用n-2个分量重构故障信号,得到降噪后的故障信号. 图 3所示为经LMD-ICA算法降噪后的故障信号及噪声分量.降噪后的故障信号可表示为
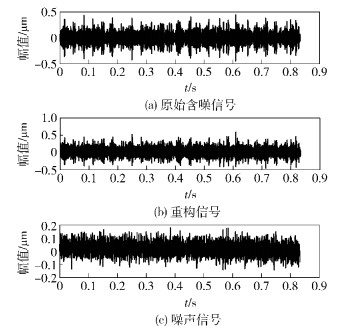
|
图 3 LMD-ICA方法分解的重构 |
| $ \bar X = \sum\limits_{i = 1}^n {\left( {I\left( {{c_i}} \right)} \right)} = \sum\limits_{i = 1}^{n - 2} {{c_{{\rm{r}}i}}} $ | (4) |
其中:X为去噪后的故障信号,I(ci) 为对第i个PF进行ICA处理.
4) 进一步对降噪后的信号进行LMD或功率谱计算,提取故障特征.
2.2 降噪效果评价为了直观、准确地评价LMD-ICA算法的降噪效果,利用Matlab产生一个信噪比 (SNR, signal to noise ratio) 为3的原始信号sref,并叠加高斯信号s.选择sym8小波进行5层分解得到小波变换与双树复小波变换的时频信号[9-10],同时对信号进行LMD时空滤波和LMD-ICA滤波,其降噪效果如图 4所示.
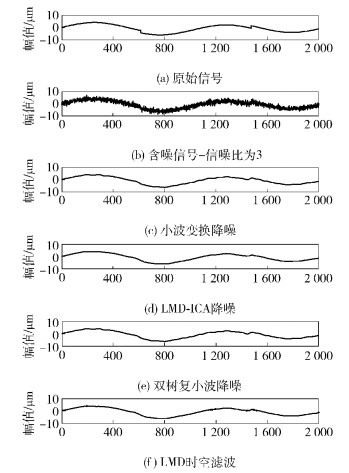
|
图 4 不同算法的降噪效果 |
由图 4可知,用LMD-ICA算法降噪时得到了较平滑的曲线,并能较好地还原原始信号曲线模型;LMD时空滤波时,仍存在较少的噪声信号;而小波变换和双树复小波变换虽能够还原原始信号曲线模型,但波形局部较振荡,滤波效果不是很理想.
从图 4可以定性地看出LMD-ICA算法降噪较其他算法的优越性,为了定量地验证LMD-ICA算法的降噪效果,通过Matlab采用SNR和均方根误差 (RMSE, root mean square error)2项指标来对该算法的降噪性能加以评价[11],将这4种方式的降噪信号与原含噪信号的SNR和RMSE做比较,结果如表 1所示.
|
|
表 1 不同算法的降噪对比 |
由表 1可以看出,通过LMD-ICA算法对含噪信号进行降噪,其降噪后的SNR值明显大于其他降噪算法,RMSE值明显小于其他降噪算法,说明LMD-ICA算法对含噪信号的降噪效果较好.
3 基于LMD-ICA的滚动轴承故障诊断实验验证对某旋转机械的滚动轴承故障信号进行采集,滚动轴承为SKF6205,转速为1 480 r/min,表 2所示为轴承各部件故障频率.
|
|
表 2 轴承各部件故障频率 |
采集时在滚动轴承轴向安装1个DH131传感器,径向安装3个DH187传感器,以径向传感器所采集的故障信号为研究对象.将经LMD-ICA算法降噪后的重构信号分别进行功率谱计算和再次LMD两种方式来提取故障特征,图 5为对重构故障信号进行功率谱计算得到的时域和频谱.
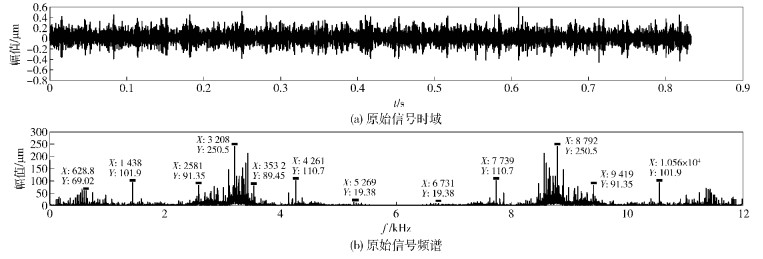
|
图 5 重构故障信号的时域和频谱 |
从图 5(b)可以看出,轴承自由端垂直方向的频谱中2倍频的幅值大于转频幅值,意味着该轴承安装时可能存在不对中现象,产生主轴转动故障;在频率为146.5 Hz时,出现了较大幅值,意味着轴承在此处冲击很大,可能会出现故障,应加强防范;在频率为235.5、353、470.5 Hz处,其频率间隔均为117.5 Hz,与轴承的外圈故障频率很接近,意味着该机床轴承存在外圈故障.
将LMD-ICA降噪后得到的重构信号再次进行LMD,分解如图 6所示.抑制LMD的端点效应后降低了噪声,再次LMD后得到了6个真实分量.将第6个分量当作噪声,将提取的前5个分量的故障特征频率与输入时计算得出的5种故障类型特征频率做相关分析,得到的相关系数与预设置的相关选择系数比较,保留符合条件的故障特征所对应的故障类型分量,再对所保留的故障类型分量求其能量值,最后对所得到的能量值进行归一化处理[7],结果如表 3所示.
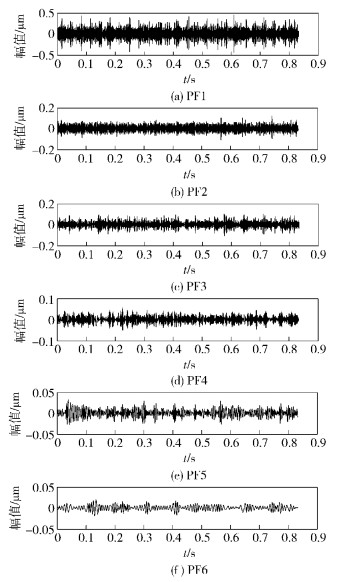
|
图 6 降噪后LMD得到的分量 |
|
|
表 3 能量提取 |
通过表 3可以看出,经过LMD-ICA分解后所提取的能量值用B表示,其中提取的能量值B1最大,其与轴系的转动频率相对应,意味着该轴承安装时可能存在不对中现象,存在主轴转动故障;其次,B2的值也较大,意味着该轴承外圈存在故障;B3、B4、B5的能量值均较小,可认为其部件正常,没有对轴承的正常运行产生影响.由图 5和表 3得出的轴承故障类型一致,且与实际情况相符合,说明LMD-ICA算法可以对含噪信号进行降噪并对含噪信号实现盲源分离.
4 结束语针对LMD和ICA各自在信号处理方面的优缺点,提出了基于LMD-ICA降噪的盲源分离算法.该方法具有以下特点:①提出的自适应波形匹配法抑制了LMD的端点效应,解决了LMD时会产生虚假PF分量的问题,克服了单通道ICA盲源分离时的欠定问题;②提出了LMD-ICA降噪算法,减少了噪声,提高了SNR,降低了RMSE;③算法可有效应用于滚动轴承的故障诊断,对滚动轴承的故障类型能够准确识别.
| [1] | Huang N E. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London a Mathematical Physical & Engineering Sciences, 1998, 454(1971): 903–995. |
| [2] |
王建国, 李健, 万旭东. 基于奇异值分解和局域均值分解的滚动轴承故障特征提取方法[J]. 机械工程学报, 2015, 51(3): 104–110.
Wang Jian guo, Li Jian, Wan Xu dong. Fault feature extraction method of rolling bearings based on singular value decomposition and local mean decomposition[J]. Journal of Mechanical Engineering, 2015, 51(3): 104–110. |
| [3] |
李志农, 刘卫兵, 易小兵. 基于局域均值分解的机械故障欠定盲源分离方法研究[J]. 机械工程学报, 2011, 47(7): 97–102.
Li Zhinong, Liu Weibing, Yi Xiaobing. Underdetermined blind source separation method of machine faults based on local mean decomposition[J]. Journal of Mechanical Engineering, 2011, 47(7): 97–102. |
| [4] |
张俊红, 李林洁, 刘海, 等. 基于经验模态分解和独立成分分析的柴油机噪声源识别技术[J]. 内燃机学报, 2012, 30(6): 544–549.
Zhang Junhong, Li Linjie, Liu Hai. Identification of diesel engine noise source based on empirical mode decomposition and independent component analysis using EMD-ICA[J]. Transaction of CSICE, 2012, 30(6): 544–549. |
| [5] |
许同乐, 张新义, 裴新才, 等. EMD遗传神经网络方法[J]. 北京邮电大学学报, 2012, 35(5): 68–72.
Xu Tongle, Zhang Xinyi, Pei Xincai, et al. EMD genetic neural networks method[J]. Journal of Beijing University of Posts and Telecommunications, 2012, 35(5): 68–72. |
| [6] | Wang Y, He Z, Zi Y. A comparative study on the local mean decomposition and empirical mode decomposition and their applications to rotating machinery health diagnosis[J]. Journal of Vibration & Acoustics, 2010, 132(2): 613–624. |
| [7] |
许同乐, 侯蒙蒙, 蔡道勇, 等. FastICA遗传神经网络算法[J]. 北京邮电大学学报, 2014, 37(4): 25–28.
Xu Tongle, Hou Mengmeng, Cai Daoyong, et al. FastICA genetic neural networks method[J]. Journal of Beijing University of Posts and Telecommunications, 2014, 37(4): 25–28. |
| [8] |
程军圣, 张亢, 杨宇, 等. 局部均值分解与经验模式分解的对比研究[J]. 振动与冲击, 2009, 28(5): 13–16.
Cheng Junsheng, Zhang Kang, Yang Yu. Comparison between the method of local mean decomposition and empirical mode decomposition[J]. Journal of Vibration and Shock, 2009, 28(5): 13–16. |
| [9] |
曲从善, 路廷镇, 谭营. 一种改进型经验模态分解及其在信号消噪中的应用[J]. 自动化学报, 2010, 36(1): 67–73.
Qu Cong-shan, Lu Ting-zhen, Tan Ying. A modified empirical mode decomposition method with applications to signal de-noising[J]. Acta Automatica Sinica, 2010, 36(1): 67–73. |
| [10] | Gan Y, Sui L, Xiao G, et al. EMD de-noising theory considering static and dynamic conditions and its applications in INS[M]. Berlin Heidelberg: Springer, 2013: 507-515. |
| [11] |
喻敏, 王斌, 王文波, 等. 联合EMD与核主成分分析的激光陀螺信号消噪[J]. 武汉大学学报 (信息科学版), 2015, 40(2): 233–237.
Yu Min, Wang Bin, Wang Wenbo. Laser gyro signal de-noising based on EMD and kernel principal component analysis[J]. Geomatics and Information Science of Wuhan University, 2015, 40(2): 233–237. |


