为了实现对频谱资源最大限度再利用,有效缓解无线频谱资源紧缺的问题,通过分析无线认知网络共享方式下的物理连接和图论模型,建立了具有不同干扰强度频谱分配数学模型,并将此模型转换为以信道干扰系数最小化、次网络效益最大化和主用户最大干扰最小化的多目标优化问题,进而采用多目标改进遗传算法对认知无线网络进行频谱共享方案设计,且对其有效性进行了仿真分析。仿真结果表明,采用所提出的优化算法进行频谱分配与图论K-最大割方法相比,能更好地实现网络效益最大化,同时能减少对主系统的干扰。
Cognitive radio is regarded as a promising technology to improve spectrum utilization significantly. Studies are put to discuss underlay spectrum sharing and power control, but issues such as the interference of the primary system are also considered as the constraint. The article builds up a spectrum allocation mathematical model which considers different interference intensity according to relative geographic locations between two SLs in the spectrum-sharing mode of cognitive radio network. Then it is converted into multi-objective optimization problem. To solve the spectrum sharing problem, the multi-objective improved genetic algorithm was adopted. Simulation shows that the proposed methods greatly outperform the commonly used K-max-cut in graph theory. It can realize the network benefit maximization and reduce the disturbance to the primary system by using the multi-objective optimization algorithm.
随着各种无线通信业务的持续发展,频谱资源变得越来越紧缺[1].为了提高有限频谱资源的利用率,在认知网络中用动态频谱共享机制来弥补现有静态频谱资源分配方式的不足,进而提高频谱的使用效率[2].目前,认知无线电系统主要有机会式 (overlay) 频谱共享和覆盖式 (underlay) 频谱共享2种频谱共享模型.现有的频谱分配方法主要有博弈论[3]、拍卖理论[4-5]和图论等方法. Qiu等[6]首次将图论用于覆盖式共享方式下的频谱共享优化问题,并将频谱共享问题转化为图论中的K-最大割问题,利用ε算法逼近优化问题的最优解,但仅仅考虑了次系统的网络效益. Elnainay [7]和柴争义等[8]将智能优化算法引入频谱分配并进行改进,证明了其可行性.
笔者提出了基于多目标优化算法的认知无线网络覆盖式频谱共享方法.在次链路终端发射功率约束和主用户接收干扰功率峰值约束的条件下,考虑无线信道中瑞利衰落的情况,结合次系统网络效益和主系统受到次系统的干扰建立多目标函数,并通过对比实验及仿真,验证了算法的可行性和优越性.
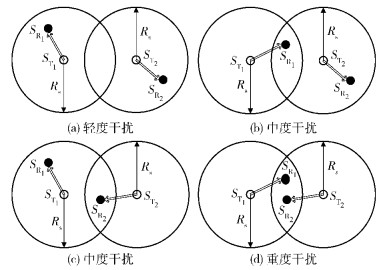
1 频谱共享物理模型建立认知无线网络中,假设次级网络采用单跳方式通信,而主网络采用蜂窝组网,由一个主基站和多个主用户组成.在一个X×Y的区域中,认知无线网络由S个次级链路和P个主链路组成,链路通常由一对发射机和接收机组成,次级链路用 (STx, SRx) 表示,每个次级链路的发射机和接收机固定配对.假设主用户可用的频谱分为M个完全正交的频段,次链路在满足频谱共享规则的前提下,可以同时使用多个频谱.次链路间的干扰由其相对地理位置上的相互距离来决定,每个次发射机都有一个所能干扰的最大范围,称为干扰半径,记为Rs. 2个次链路的相对地理位置可分为4种情况,如图 1所示.
|
图 1 次链路的相对地理位置 |
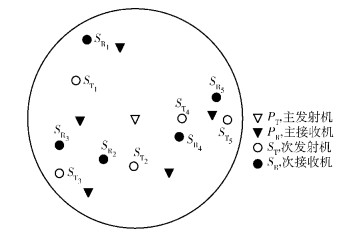
根据次链路之间的相对地理位置,其相互之间的干扰可量化为轻度干扰、中度干扰、重度干扰3个等级.对应的干扰因子分别表示为f0、f1、f2,3种干扰因子满足关系f0 < f1 < f2. 表 1给出了图 2所示认知无线网络系统模型对应的干扰因子矩阵,FS×S={f(SL, xi, SL, xj)|f(SL, xi, SL, xj)∈{f0, f1, f2}, xi≠xj}S×S,其中SL, xi, SL, xj, i、j∈{1, 2, 3, 4, 5}表示次级链路.
|
|
表 1 干扰因子矩阵 |
|
图 2 认知无线网络系统模型 |
在认知无线网络应用环境中,网络的拓扑结构会随着环境的变化而发生改变,其改变可以通过每个周期的检测报告获得.由于认知无线网络系统进行频谱分配的时间相对于频谱环境变化的时间很短,所以,假定一个检测周期内的系统拓扑结构不会发生改变.
2 多目标下频谱资源优化分配 2.1 问题的描述及分析假设主用户可用的信道数是M,次发射机ST1与次接收机SR2、次发射机ST与主接收机PR以及主发射机PT与次接收机SR在信道m上的信道增益可以分别表示为gss(m, ST1, SR2)、gsp(m, ST, PR) 以及gps(m, PT, SR),其中信道增益由大尺度衰落和小尺度衰落2部分组成.在信道m上次发射机ST以及主发射机PT的发射功率分别表示为Ps(m, ST) 和Pp(m, PT). SL, x表示次级链路,由于每个次链路SL, x都有信道需求CSL, x,所以信道分配矩阵必须满足次链路信道需求约束,即有式 (1) 成立,为方便起见,各次链路信道需求取相同的定值.
| $ \sum\limits_{m = 1}^M {a\left( {m,{S_{L,x}}} \right)} = {C_{{S_{\rm{L}}}}} $ | (1) |
又由于在Underlay频谱共享中,只有次用户在对主用户的干扰小于给定门限值的条件下才可以与主用户共享同一段频谱,同时,次发射机有一个最大发射功率,次发射机在各个频段上的发射功率之和不能超过最大发射功率,有式 (2) 和式 (3) 成立.
| $ \sum\limits_{{S_{\rm{T}}} \in I} {{P_{\rm{s}}}\left( {m,{S_{\rm{T}}}} \right){g_{{\rm{sp}}}}\left( {m,{S_{\rm{T}}},{P_{\rm{R}}}} \right)} \le I_{{P_{\rm{R}}}}^m $ | (2) |
| $ \sum\limits_{m \in {W_{{S_{{\rm{Tx}}}}}}} {{P_{\rm{s}}}\left( {m,{S_{{\rm{Tx}}}}} \right)} \le P_{\rm{s}}^{\max } $ | (3) |
其中:WSTx为次发射机STx分配到的频谱集合,IPRm为主接收机PR在信道m上的干扰温度约束,Psmax为次发射机的最大发射功率.
分析认知无线网络频谱分配时,首要考虑的是次网络的网络效益,因此次接收机SRx(对应的次发射机为STx) 在信道m上的接收信干噪比可以表示为
| $ {\gamma _{\rm{s}}}\left( {m,{S_{{\rm{L}},x}}} \right) = {S_{\rm{s}}}/\left( {{N_{\rm{s}}} + {N_{\rm{p}}} + {P_{{N_0}}}} \right) $ | (4) |
其中:Ss为次链路的有用信号,Ss=gss(m, STx, SRx)Ps(m, STx)a(m, STx);Ns为来自其他次链路的干扰,Ns=
| $ {r_{\rm{s}}}\left( {m,{S_{{\rm{Tx}}}}} \right) = {\rm{lb}}\left( {1 + {\gamma _{\rm{s}}}\left( {m,{S_{{\rm{Tx}}}}} \right)} \right) $ | (5) |
次链路在信道m上的可达速率还取决于信道分配结果.在此定义一个信道分配矩阵:
| $ {\mathit{\boldsymbol{A}}_{M \times S}} = {\left\{ {a\left( {m,{S_{{\rm{L}},x}}} \right)\left| {a\left( {m,{S_{{\rm{L}},x}}} \right)} \right. \in \left\{ {0,1} \right\}} \right\}_{M \times S}} $ | (6) |
其中:a(m, SL, x)=1表示将信道m分配给次链路SL, x,a(m, SL, x)=0表示没有将信道m分配给次链路SL, x.只有当信道m分配给次链路时,才能够获得相应的可达速率.因此,所有次链路的速率总和可以表示为
| $ \begin{array}{*{20}{c}} {R_{\rm{s}}^{{\rm{total}}} = \sum\limits_{x = 1}^S {{R_{\rm{s}}}\left( {{S_{{\rm{L}},x}}} \right)} = }\\ {\sum\limits_{x = 1}^S {\sum\limits_{m = 1}^M {{r_{\rm{s}}}\left( {m,{S_{{\rm{L}},x}}} \right)a\left( {m,{S_{{\rm{L}},x}}} \right)} } } \end{array} $ | (7) |
| $ \max R_{\rm{s}}^{{\rm{total}}} = \sum\limits_{x = 1}^S {{R_{\rm{s}}}\left( {{S_{{\rm{L}},x}}} \right)} $ | (8) |
次链路的速率总和越大,整个系统的频谱利用率越高.
认知无线网络基于Underlay的频谱共享问题就是求信道分配矩阵AM×N,根据图论中的K-最大割问题分析,信道分配的目标是保证分配到同一频段内各链路之间的干扰因子之和最小化,把每个信道上的干扰因子之和称为该信道的干扰系数,表示为
| $ {F_m} = \sum\limits_{{x_i} = 1}^S {\sum\limits_{{x_j} = {x_i} + 1}^S {a\left( {m,{S_{{\rm{L}},{x_i}}}} \right)a\left( {m,{S_{{\rm{T}},{x_j}}}} \right)f\left( {{S_{{\rm{L}},{x_i}}},{S_{{\rm{T}},{x_j}}}} \right)} } $ | (9) |
| $ \min {F_{{\rm{mean}}}} = \frac{1}{M}\sum\limits_{m = 1}^M {{F_m}} $ | (10) |
式 (10) 保证了平均干扰系数最小化,即保证了分配到同一频谱内的各次用户之间的干扰最小.另外,在频谱分配中还要保证对主用户的干扰越小越好,因此使主用户受到的干扰最小化.式 (11) 表示主用户PR在频谱m上受到的干扰,最小化最大干扰即可保证所有主用户受到的干扰均在干扰温度之内.
| $ I_{{P_{{{\rm{R}}_p}}}}^m = \sum\limits_{x = 1}^S {I\left( {{P_{R,p}},m,{S_{{\rm{L}},x}}} \right)} $ | (11) |
| $ \min {I_P} = \max \left( {\sum\limits_{x = 1}^S {I\left( {{P_{R,p}},m,{S_{{\rm{L}},x}}} \right)} } \right) $ | (12) |
其中I(PR, p, m, SL, x) 为主用户PR, p在频谱m上受到次发射机STx对其干扰大小.
将最小化平均干扰系数、最小化最大主用户受到的干扰、最大化整个系统的频谱利用率作为3个优化目标.设置约束条件为:①次级链路的信道需求约束;②次级发射机的最大发射功率约束;③主接收机的干扰温度约束.从而把基于Underlay方式的频谱共享问题建模为式 (13) 的优化问题.
| $ \left. \begin{array}{l} \min {f_1}\left( X \right) = \frac{1}{M}\sum\limits_{m = 1}^M {{F_m}} \\ \min {f_2}\left( X \right) = \max \left( {\sum\limits_{x = 1}^S {I\left( {{P_{R,p}},m,{S_{{\rm{L}},x}}} \right)} } \right)\\ \min {f_3}\left( X \right) = \sum\limits_{x = 1}^S {{R_{\rm{s}}}\left( {{S_{{\rm{L}},x}}} \right)} \\ {\rm{s}}{\rm{.t}}{\rm{.}}\left\{ \begin{array}{l} \sum\limits_{m = 1}^M {a\left( {m,{S_{{\rm{L}},x}}} \right)} = {C_{{S_{\rm{L}}}}}, \forall x = 1,2, \cdots ,N\\ \sum\limits_{m \in {W_{{S_{{\rm{Tx}}}}}}} {{P_{\rm{s}}}\left( {m,{S_{{\rm{T}},x}}} \right) \le P_{\rm{s}}^{\max }} , \forall x = 1,2, \cdots ,N\\ \sum\limits_{{S_{\rm{T}}} \in I} {{P_{\rm{s}}}\left( {m,{S_{\rm{T}}}} \right){g_{{\rm{sp}}}}\left( {m,{S_{\rm{T}}},{P_{\rm{R}}}} \right)} \le I_{{P_{\rm{R}}}}^m \end{array} \right. \end{array} \right\} $ | (13) |
采用改进非支配排序遗传算法 (NSGA-Ⅱ, nondominated sorting genetic algorithm version Ⅱ) 来解决Underlay频谱共享问题,以每个次用户的频谱分配方式a(:, SL, x)(∀x=1, 2, …, S) 作为基因,所有次用户的频谱分配方式组成分配方案作为个体,多个分配方案构成分配方案集作为种群.首先通过十进制整数编码提高算法的运算效率,利用非支配算子进行快速排序;然后在非支配排序的基础上按个体拥挤距离排序选择,以保持种群的多样性;最后采用精英策略保留父代中的优良个体直接进入子代,以防止获得的Pareto最优解丢失.
1) 为了满足次链路信道需求约束,首先要采用二进制编码出长度为M的基因库,其中每个基因要满足次链路信道需求约束
2) 随机产生规模大小为L的初始种群A(g)={Agi|Agi=[a1, a2, …, as], i=1, 2, …, L},每个个体由S个基因组成,种群中的每个个体代表了一种可能的优化频谱分配方案;经过遗传操作产生新的子种群A′(g),此时令g=0.
3) 合并父代子代种群. A″(g)=A(g)∪A′(g),对A″(g) 进行非劣排序,得到非劣前沿F1、F2、…、Fn.
4) 当产生的前m个前沿中的个体总数大于总数L时,停止分层排序.将前m个前沿依次填入下一代中,对第m个前沿先进行拥挤度排序,取最稀疏的个体填至总数为L.
5) 对种群A(g+1) 进行复制、遗传操作,形成种群A′(g+1).
6) 如果达到终止条件,则退出;否则g=g+1,程序执行3).
2.3 最优折衷解的选择对进化Gmax代后产生的AGmax选出非劣等级为1的非支配集进行解码操作,生成频谱共享方案,对于多目标优化算法,最后输出的Pareto最优解可能有多个,即生成的候选接入方案可能有多个,此时根据模型式 (14) 确定接入方案.
| $ \arg \min \left\{ {\frac{{{f_2}\left( {{X_j}} \right)}}{{{f_{2\min }}}} + \frac{{{f_3}\left( {{X_j}} \right)}}{{{f_{3\min }}}}} \right\},j = 1,2, \cdots ,J $ | (14) |
其中:J为优势个体个数,fmin为Pareto最优解集中fi(X)(i=2, 3) 的最小值.目标1是为了获得更好的网络效益所设的,因此在此不予考虑;又因为每个共享方案中主用户受到的干扰和次网络的效益不能同时最优,但系统希望f2(X)/f2min与f3(X)/f3min越小越好,所以模型式 (14) 是f2(X) 和f3(X) 较好的折中.
3 仿真实验与结果分析仿真实验环境是在一个半径为200 M的圆形区域内,主基站位于圆心处,主接收机和次发射机均匀分布在圆内.次发射机的位置确定后,其对应的次接收机均匀分布于以次发射机为圆心,半径为80 M的圆内,并且每条链路都有最小距离约束.另外,信道增益由大尺度衰落和小尺度衰落2个部分组成.其中,大尺度衰落采用自由空间传播模型d-α,d为发射机和接收机之间的距离,α为衰落因子,通常取3.5;小尺度衰落服从瑞利分布.仿真参数如表 2所示.
|
|
表 2 仿真参数 |
智能优化算法的参数分别设置为:种群规模L=200,最大迭代次数Gmax=400,交叉概率pc=0.9,变异概率pm=0.1,交叉算子muc=20,变异算子mum=20.
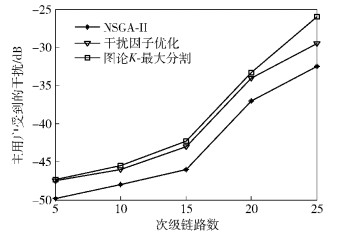
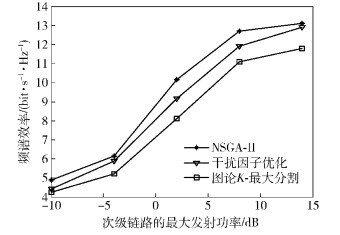
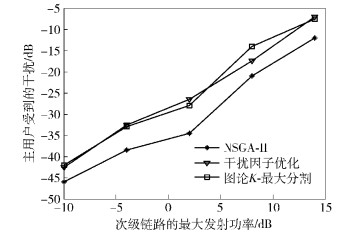
由图 3可以看出,随着次级链路数的增加,网络负载增大,主用户受到的干扰呈增长趋势,但是所提算法中主用户受到的干扰明显小于已有的2种算法,从而验证了所提算法的优越性.同时也验证了在次级链路数为15的情况下,次级链路最大发射功率变化对频谱效率和主用户受到的干扰情况的影响,结果如图 4和图 5所示.可以看出,随着次级链路的发射功率的增大,所有算法频谱效率随之提升,并且主用户受到的干扰也会明显增加.这是由于随着次发射机功率的增大,次级链路之间的干扰成为主要干扰来源,以干扰因子抑制为目标的NSGA-Ⅱ能取得更好的干扰抑制效果;另外,由于多条链路共享一个频段,当次级链路功率增大时,某次级链路受到的干扰增加会快于其有用信号的增加,所以随着次级链路功率的增加频谱效率的增加会慢慢变缓,进一步表明了所提算法的有效性.
|
图 3 不同算法下主用户受到的干扰对比 |
|
图 4 频谱效率与次链路最大发射功率的关系 |
|
图 5 主用户受到的干扰与次链路最大发射功率的关系 |
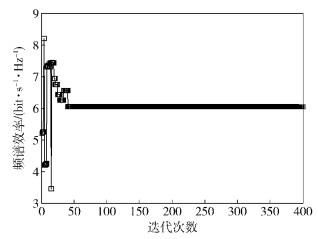
最后验证了在次级链路数为15以及次级链路最大发射功率为-5 dB的情况下NSGA-Ⅱ的收敛性情况.由图 6可以看出,利用NSGA-Ⅱ求解频谱效率和主用户受到的干扰情况时,迭代50次左右都能收敛到最优解.
|
图 6 频谱效率的收敛性 |
笔者利用多目标改进遗传优化算法解决了Underlay共享方式下的频谱共享问题,综合考虑了次系统的网络效益和主系统受到的干扰情况两个主要目标,并与图论K-最大割方法和基于图论的干扰因子优化算法进行了性能比较.仿真结果表明,智能优化算法适用于解决Underlay频谱共享问题,并且在次系统的网络效益和主系统受到的干扰情况两个方面均能取得较好的结果.
| [1] |
文凯, 傅小玲, 陈小洪, 等. 认知中基于业务和信道分级的分布式信道分配[J]. 计算机工程与设计, 2012, 33(9): 3381–3385.
Wen Kai, Fu Xiaoling, Chen Xiaohong, et al. Distributed channel allocation algorithm based on classifying of services and channels in cognitive radio networks[J]. Computer Engineering and Design, 2012, 33(9): 3381–3385. |
| [2] | Liang Yingchang, Chen Kwang C, Li Geoffrey Y, et al. Cognitive radio networking and communications:an overview[J]. IEEE Transactions on Vehicular Technology, 2011, 60(7): 3386–3407. doi: 10.1109/TVT.2011.2158673 |
| [3] |
黄丽亚, 刘臣, 王锁萍, 等. 改进的认知无线电频谱共享博弈模型[J]. 通信学报, 2010, 31(2): 136–140.
Huang Liya, Liu chen, Wang Suoping, et al. Improved spectrum sharing model in cognitive radios based on game theory[J]. Journal on Communications, 2010, 31(2): 136–140. |
| [4] | Gandhi S, Buragohain C, Cao Lili, et al. Towards real time dynamic spectrum auctions[J]. Computer Networks, 2009, 52(4): 879–897. |
| [5] | Niyato D, Hossain E. Dynamics of multiple-seller and multiple-buyer spectrum trading in cognitive radio networks:a game theoretic modeling approach[J]. IEEE Transactions on Mobile Computing, 2009, 8(8): 1009–1022. doi: 10.1109/TMC.2008.157 |
| [6] | Qiu Tao, Xu Wenjun, He Zhiqiang, et al. Graph-based spectrum sharing for multiuser OFDM cognitive radio networks[C]//Wireless Communication and Signal Processing. [S.l.]:[s.n.], 2011:1-5. |
| [7] | Elnainay M Y. Island genetic algorithm-based cognitive networks [D]. Blacksburg:Virginia Polytechnic Institute and State University, 2009. |
| [8] |
柴争义, 刘芳. 基于免疫克隆选择优化的认知无线网络频谱分配[J]. 通信学报, 2010, 31(11): 92–100.
Chai Zhengyi, Liu Fang. Spectrum allocation of cognitive wireless network based on immune clone selection optimization[J]. Journal on Communications, 2010, 31(11): 92–100. doi: 10.3969/j.issn.1000-436X.2010.11.014 |


