2. 哈尔滨理工大学 机械动力工程学院, 哈尔滨 150080
针对时间约束有向无环图表示的业务流程工作流准确率优化问题,提出了基于截止期的逆向归约优化算法,摒弃传统算法的单向目标策略,解决了业务流程完工准确率过低或者完工时间过长的问题。通过整合传统算法遗留下来的时间碎片,分析了服务准确率与时间的制约关系,以逆向归约方式求出优化路径。模拟数据表明,逆向归约优化算法能够实现截止期范围内时间与准确率的平衡,相比于传统算法在相同约束时间下对准确率起到了优化效果。通过分析业务流程的截止期大小和任务数对算法性能的影响可知,截止期或任务数的增大提升了算法优化效果。
2. School of Mechanical Engineering, Harbin University of Science and Technology, Harbin 150080, China
Aiming at optimizing accuracy in business process workflow represented by directed acyclic graph (DAG) in time constraint, the reverse reduction optimization algorithm (RRO) based on deadline was proposed. This algorithm gives up one-way target strategy of traditional algorithm and eliminates the problems of the low accuracy or high completion time of business process. By integrating the time debris left by the traditional algorithm and analyzing the relationship between the accuracy and the time of the service, the optimal path is obtained by reverse reduction. Simulation shows that the reverse reduction optimal algorithm can achieve the balance between completion time and completion accuracy in the range of deadline. Furthermore, the influence of the performance to the algorithm when it applies to different deadlines and different numbers of tasks is analyzed by different simulation data and the increasing of the deadline or the number of tasks improves the algorithm optimization performance.
以服务为结点映射到网络流从而建立有向无环图 (DAG,directed acyclic graph) 是供应链技术建模之一[1],在规定的时间范围内选择合理的服务对优化工作流起着关键性作用.针对混合式工作流,以时间启发函数为基础,通过遗传算法或者动态重排策略可有效地减少成本[2-3];以关键路径的完工时间与截止期对任务环节扩大活动范围,进而确定时间与成本的制约关系来实现成本的优化[4-5].
笔者的贡献主要在于提出了一种基于复杂产品工作流在约束时间内控制任务的执行区间,进而优化准确率的逆向归约优化算法,并通过准确率监测点检测反馈,实现准确率的提升[6].
1 问题描述 1.1 工作流模型的相关定义工作流建模是将业务流程映射到DAG中,是利用业务所有信息进行构图的过程.
定义1 任务池.即产品制造过程中所有任务组成的集合,用P表示,P=(p1, p2, …, pi, …, pn).
定义2 服务池.即任务池P中任意元素pi对应的服务集合.用Si表示,则Si=(s1, s2, …, sj, …, sm).
定义3 服务池的秩.即任务p对应的服务池中可以完成该任务的服务个数,表示为rp.
定义4 准测点.业务流程完工时对准确率进行检测,若未达到限定准确率的要求,则反馈循环,重新加工;若达到限定准确率要求,则进入后续环节,进行加工.准测点用M表示,对应的值表示为ξ.考虑到成本问题,笔者仅进行1次循环.
定义5 工作流图.若用G表示,可形式化为四元组G={spk, E, M, Sp},spk为任务p用其对应的服务池Sp中的第k个服务完成,E为有向边,表示结构流程,Sp为任务p的服务池,且工作流图中存在结点ps和结点pe,分别表示为业务流程的开始和结束.
定义6 服务属性.是指工作流图G中服务spk完成任务p所花费的时间和达到的准确率,表示为ptpk=(tpk, apk),其中p∈P,0 < k ≤ rp,tpk为花费的时间,apk为达到的准确率.
1.2 工作流的约束分析定义7 完工时间.通过对每个任务p配置一个服务来实现整个工作流程的完工,其所花费的时间,表示为T.
定义8 完工准确率.通过对每个任务p配置一个服务来实现整个工作流程的完工,其所达到的准确率,表示为A.
定义9 完工截止期.指工作流程的完工约束时间,表示为ψ.
工作流的调度是建立在完工时间低于截止期的前提下才进行优化的,这一约束条件可形式化为
| $ \left. \begin{array}{l} A = \prod {{l_{pk}}{a_{pk}}} + A' \ge \xi \\ T = \sum {{l_{pk}}{t_{pk}}} + T' \ge \psi \\ p \in P, 0 < k \le {r_p} \end{array} \right\} $ | (1) |
其中:A′为经过反馈后提升的准确率,T′为多花费的时间.
| $ \left. \begin{array}{l} {\rm{s}}{\rm{.t}}{\rm{.}} \sum\limits_{k = 1}^{{r_p}} {{l_{pk}}} = 1\\ {l_{pk}} \in \left\{ {0,1} \right\}\\ p \in P, 0 < k \le {r_p} \end{array} \right\} $ | (2) |
式 (1) 表示完工时间与准确率相对应的制约关系,即必须在截止期范围内以求得准确率;式 (2) 中的lpk为一个变量,表示当执行某个任务时只能选择其服务池中一个服务来完成.
2 传统单向目标算法传统单向目标算法策略是基于当前最优解的,即都选择执行时间最短的服务或者执行准确率最大的服务.
2.1 基于时间最小化的算法策略在每层任务中选择完成时间最小的服务,形成一条工作流路径,求解该方法的准确率为
| $ \left. \begin{array}{l} T = \sum {\min \left( {{t_{pk}}} \right) + T'} \\ A = \prod {{a_{pk}} + A', 0 < k < {r_p}} \\ p \in P \end{array} \right\} $ | (3) |
实现完工准确率最大化,即每个任务由服务集合中准确率最大的服务来完成,完工准确率才能达到最大化,计算该策略的完工时间为
| $ \left. \begin{array}{l} A = \prod {\max \left( {{a_{pk}}} \right) + A'} \\ T = \sum {{t_{pk}} + T', 0 < k \le {r_p}} \\ p \in P \end{array} \right\} $ | (4) |
定义10 任务自由度Wp.即工作流模型中任务p的开始时间组成的集合,表示为Wp=[Rp,Np],p∈P,其中Rp为任务p最早开始的时间,Np为任务p最晚开始的时间,有
| $ \left. \begin{array}{l} {R_p} = \sum\limits_{i = 1}^{p - 1} {\min \left( {{t_{ik}}} \right)} , 0 < k \le {r_p},{R_1} = 0\\ {N_p} = \psi - \sum\limits_{i = n}^p {\min \left( {{t_{ik}}} \right)} , 0 < k \le {r_p} \end{array} \right\} $ | (5) |
逆向归约优化算法 (RRO,reverse reduction optimization algorithm) 通过分析时间与准确率的制约关系,在截止期的基础上实现每个任务环节的分层,建立任务自由度,使每个任务能对服务进行更大范围的选择.笔者以任务的自由度为基础,求出每个任务p的自由度Wp,采用由后至前的方式求解每个任务在不同时刻开始时能达到的最大准确率,当遍历到初始任务时,则表示此段工作流程的结束,以此与准测点比较反馈,最终确定约束时间内准确率得到优化的路径.
假设业务流程包含n个任务,令f(p, t) 为第p个任务从t时刻开始能达到的最大准确率,t∈[Rp, Np].最后1层任务在对应的自由度区间内,在不同时刻开始时必然能得到1个准确率最大值,有
| $ \left. \begin{array}{l} f\left( {p,{t_p}} \right) = \max \left\{ {{a_{pk}}} \right\},p = n,0 < k \le {r_p}\\ {t_p} \in \left[ {{R_p},{N_p}} \right],{t_p} + {t_{pk}} \le \psi \end{array} \right\} $ | (6) |
存在任务p′,满足p′为任务p的前驱任务,对整个业务的任务归约后,利用最后1层的任务,依次向前求得每个任务在不同时刻开始时的准确率最大值,有
| $ \left. \begin{array}{l} f\left( {p',{{t'}_p}} \right) = \max \left\{ {{a_{p'k}}f\left( {p,{t_{p'}} + {t_{p'k}}} \right)} \right\}\\ {t_{p'}} \in \left[ {{R_{p'}},{N_{p'}}} \right] \end{array} \right\} $ | (7) |
通过层层迭代,当遍历到初始任务时,即可得到每完工时间下的最大准确率.
定理1 一个完整的业务流程若存在f(n, t) 为截止期ψ下的最大准确率,则在截止期ψ-t0下的最大准确率为f(n, t+t0).
证明 已知在截止期ψ下的最大准确率为f(n, t),假设ψ-t0下的最大准确率为f(n, t+t1),且t1 < t0,若f(n, t+t0)=f(n, t+t1),则定理1成立;若f(n, t+t0) < f(n, t+t1),则该情况下业务流程的完工时间ψ′必定大于ψ-t0,此时假设与规定矛盾;假设ψ-t0下的最大准确率为f(n, t+t2),且t2 > t0,则必有f(n, t+t0) ≥ f(n, t+t2),则f(n, t+t0) 为最大准确率.综上所述,定理1成立.
综上所述,RRO伪代码如下.
输入:参数P; spk; ptpk; len //len为集合R′中所有任务的数目
输出:最佳路径
By G; //通过生成的工作流图G
For (int p=1; p ≤ len; p++) {List (Formula (5), Wp); } //利用式 (5) 对工作流程相应任务取自由度Wp
p=len; Figure (Formula (6), apk); //利用式 (6) 求得最后1层任务不同时刻开始的最大准确率
For (p; p > 0; p--){Figure (Formula (7), apk); }; //利用式 (7) 依次求解前驱的任务在不同时间开始达到的最大准确率
Foreach (A){If (A < ξ){A=A+A(1-A) T=T+T′}} //对每种完工时间下的结果进行准测点检验,并循环
Search max (At) Where T≤ψ; //查找截止期内最大准确率的路径,即最佳路径
该算法的时间复杂度为O(mn).
4 实验结果与分析 4.1 案例设计经调研,某机械生产流程分为6个环节:冲压环节p1、焊接环节p2、涂装环节p3、部件装配环节p4、总装配环节p5、虚拟的申请环节ps、虚拟的竣工环节pe.其中申请和竣工作为虚拟任务,表示流程的开始和结束,设置准测点M对应的ξ=0.90,若A < ξ, 则进行反馈,多花费时间为1,假设每循环1次则多耗费诸多成本,因此当A≥0.90即完工.任务对应的服务池为Sp,属性如表 1所示.
|
|
表 1 服务时间和准确率 |
通过以上任务池P和每个任务p对应的服务池Sp,对该业务流程建立如图 1所示的工作流.
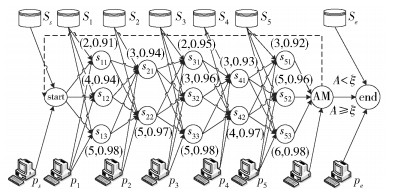
|
图 1 工作流 |
基于图 1所示的工作流,规定本业务流程的完工截止期ψ=17,分别以2种策略完成工作流.
4.2.1 传统单向目标算法策略1) 基于时间最小化的单向目标算法
基于完工时间最小化,即所有任务都选择执行时间最小的服务,则调用式 (3) 求得对应的完工时间为
T=t11+t21+t31+t41+t51+t61=13
准确率A=a11a21a31a41a51=0.695.由于A < ξ, 则进行反馈,此时
A=0.695+(1-0.695)×0.695=0.907
T=13+1=14
2) 基于准确率最大化的单向目标算法
基于完工准确率最大化,即所有任务都选择准确率最大的服务,则调用式 (4) 求得对应的Amax=a13a22a33a42a53=0.886,则对应工作流程的完工时间T=t13+t22+t33+t42+t53=25, 由于A < ξ, 则进行反馈,此时A=0.886+(1-0.886)×0.886=0.987,T=25+1=26.
4.2.2 逆向归约优化算法调用逆向归约算法可得该业务流程的任务集合P、任务对应的服务集合Sp和服务属性ptpk.冲压环节p1的自由度为[0,4],焊接环节p2的自由度为[2,6],涂装环节p3的自由度为[5,9],部件装配环节p4的自由度为[7,11],总装配环节p5的自由度为[10,14],则在对应任务的自由度内,可求出各任务在不同时刻开始达到的最大准确率,如表 2所示.
|
|
表 2 不同任务环节的计算过程 |
由表 2的结果并结合定理2可得,完工时间T={17,16,15,14,13}下最大准确率为A={0.780,0.756,0.733,0.724,0.695}.根据准测点检测结果,需要循环反馈的路径完工所用时间T′、完工准确率A′如表 3所示.
|
|
表 3 各完工时间及准确率 |
由表 3可知,反馈后准确率最大路径的完工时间为18,超过完工截止期,因此舍弃该方案,选择准确率A=0.940和完工时间T=17的优化路径.
4.3 算法比较针对传统单项目标算法和逆向归约优化算法,并结合4.2节中各数据,做出如图 2所示的算法对比结果. 图 2(a)给出了工作流程在不同算法基础上执行到不同阶段时的完工时间和准确率,图 2(b)给出了不同算法对应的完工路径.
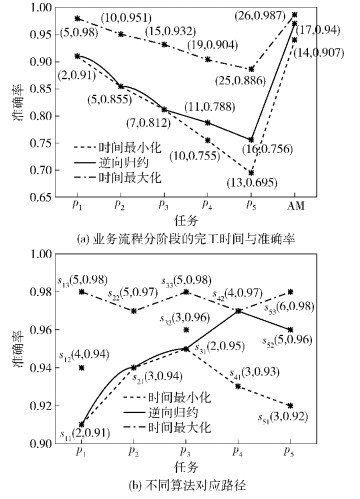
|
图 2 算法对比 |
从图 2(a)所知,基于准确率最大化算法策略的完工准确率最高,但完工时间超过了截止期,因此被舍弃.基于时间最小化算法策略和逆向归约算法策略的完工时间满足规定条件,其对应的完工准确率分别为A1=0.940、A2=0.907,可计算逆向归约算法的提高率K=(A2-A1)/A1×100%=3.63%.因此,逆向归约算法相对于传统单向目标算法起到了优化提升效果,且由图 2(b)得到的对应路径为s11→s21→s31→s42→s52.
4.4 其他参数对算法性能的影响 4.4.1 截止期ψ的大小产生的影响业务流程随着截止期ψ的增大可选择更加适合的服务,完工准确率也可得到提高.随机生成{10, 15}个任务数,每个任务服务池的大小取区间[2, 4],每个服务生成相应的属性;规定准测点M的ξ=0.90,当完工准确率低于该值时进行反馈,增加完工时间为1,且仅循环1次.假设每个业务流程的最小完工时间为Tmin,分别以Tmin增加10%、15%、20%、25%、30%作为不同的截止期,图 3体现不同的截止期对算法性能的影响.
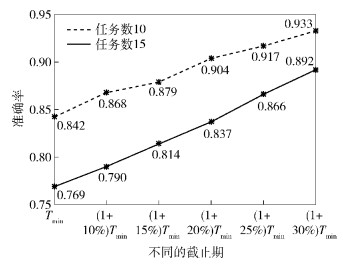
|
图 3 不同截止期ψ对算法性能的影响 |
从图 3可见,当截止期为Tmin时,即基于时间最小化策略,将任务数为10的业务流程增加10%、15%、20%、25%、30%作为截止期,逆向归约算法的提高率分别为3.1%、4.4%、7.4%、8.9%、11.0%;任务数为15的业务流程,逆向归约算法的提高率分别为2.7%、5.9%、8.8%、12.6%、16.0%.
4.4.2 任务数对性能的影响业务流程任务数的变化对总体准确率有影响,同时也影响着逆向归约算法的优化效果.随机生成{5, 10, 15, 20}个任务数,每个任务服务池的大小取区间[2, 4],每个服务并生成相应的属性;规定准测点M的ξ=0.90,当完工准确率低于该值时进行反馈,增加完工时间为1,且仅循环1次.假设每个业务流程的最小完工时间为Tmin,以Tmin增加20%作为不同流程的截止期,图 4所示为不同任务数对算法性能的影响.
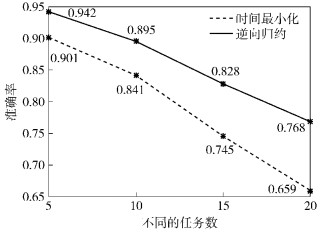
|
图 4 任务数对算法性能的影响 |
从图 4可以得出,随着任务数的增多,逆向归约优化算法的提高率分别为4.6%、6.4%、11.1%、16.5%.
5 结束语针对业务流程时间和准确率平衡问题,笔者首先将业务流程的任务环节映射到DAG中,生成工作流模型.提出了基于工作流时间最小化和准确率最大化的传统单向目标算法,针对该传统算法存在的完工准确率过低或完工时间过长的弊端,提出了在截止期约束下的逆向归约优化算法,解决了传统算法产生时间碎片等问题,能更好地利用时间,从而对每个任务选择更合理的服务.模拟实验结果表明,逆向归约优化算法相对于传统的单向目标算法,其性能提高了3.63%.笔者以截止期和任务数作为影响算法性能的参数,利用对应参数可提升算法性能.
| [1] | Czarnul P. Modeling, run-time optimization and execution of distributed work-flow applications in the JEE-based BeesyCluster environment[J]. The Journal of Supercomputing, 2013, 63(1): 46–71. doi: 10.1007/s11227-010-0499-7 |
| [2] | Nasonov D, Butakov N, Balakhontseva M, et al. Hybrid evolutionary workflow scheduling algorithm for dynamic heterogeneous distributed computational environment[J]. Springer International Publishing, 2014, 299(6): 83–92. |
| [3] | Chen Wei, Lee Youngchoon, Fekete A, et al. Adaptive multiple-work-flow scheduling with task rearrangement[J]. Journal of Supercomputing, 2015, 71(4): 1297–1317. doi: 10.1007/s11227-014-1361-0 |
| [4] |
苑迎春, 李小平, 王茜, 等. 基于逆向分层的网格工作流调度算法[J]. 计算机报, 2008, 31(2): 282–290.
Yuan Yinchun, Li Xiaoping, Wang Qian, et al. Bottom level based heuristic for workflow scheduling in grids[J]. Chinese Journal of Computers, 2008, 31(2): 282–290. |
| [5] |
刘灿灿, 张卫民, 骆志刚. 基于逆向分层的工作流时间-费用优化方法[J]. 国防科技大学学报, 2013, 35(3): 61–66.
Liu Cancan, Zhang Weimin, Luo Zhigang. Time and cost trade-off heuristics for workflow scheduling based on bottom level[J]. Journal of National University of Defense Technology, 2013, 35(3): 61–66. |
| [6] | Luo Zhiyong, Wang Peng, You Bo, et al. Serial reduction optimization research of complex product workflow's accuracy under the time constraint[J]. Advances in Mechanical Engineering, 2016, 8(10): 1–9. |


