欠定盲分离是在源信号和信道传输参数未知的情况下，仅由传感器接收到的观测信号来恢复源信号的过程，且要求传感器的个数少于源信号的个数. Mohimani等^[1]提出了基于平滑l₀范数 (SL0, smoothed l₀ norm) 的稀疏重构算法，可用于欠定盲分离源信号恢复. Eftekhari等^[2]在SL0的基础上提出了稳健SL0(RSL0, robust SL0) 方法，提高了抗噪性能. Vidya等^[3]提出了基于径向级联网络的稀疏重构 (RASR, radial basis function cascade network for sparse signal recovery) 算法，提高了重构精度.安澄全等^[4]提出了基于混合优化的SL0稀疏重构 (HOSL0, hybrid optimization SL0) 算法，降低了复杂度.上述算法均采用梯度下降法寻找最优解，然而当迭代步长选择不当时，算法的精度较差.

针对现有的算法存在的不足，笔者在径向基函数 (RBF, radial basis function) 网络的基础上，利用反馈回路进行交替优化，同时使用修正的牛顿方向进行迭代，来提高算法的收敛速度和精度.所提出的算法在保证较高恢复精度的同时显著降低了算法的复杂度，与现有算法相比，表现出了良好的恢复性能.

1 欠定盲分离模型

盲源分离在没有先验信息的情况下，仅利用观测信号来恢复源信号，其数学表达式为

$ \mathit{\boldsymbol{x}}\left( t \right) = \mathit{\boldsymbol{As}}\left( t \right) $

(1)

其中：x(t)=[x₁(t), x₂(t), …, x_M(t)]^T为观测信号向量；s(t)=[s₁(t), s₂(t), …, s_N(t)]^T为源信号向量；A∈$\mathbb{R}$^M×N为混合矩阵，M为观测信号数目，N为源信号数目，且要求M < N；t=1, 2, …, T为离散采样时刻，T为总的采样点数.当源信号为稀疏信号时，欠定盲分离可以采用两步法进行解决，首先利用接收到的信号估计出混合矩阵A，然后利用接收信号与估计出的混合矩阵恢复出源信号s(t).在混合矩阵A已经估计出来的情况下，欠定盲分离源信号恢复与压缩感知稀疏信号重构有相同的数学模型，可以使用稀疏信号重构算法来求解欠定盲分离源信号恢复问题.为了描述方便，省略式 (1) 中的t，即针对离散采样时刻t，重写式 (1) 得

$ \mathit{\boldsymbol{x}} = \mathit{\boldsymbol{As}} $

(2)

其中：x=[x₁, x₂, …, x_M]^T为观测向量，s=[s₁, s₂, …, s_N]^T为源信号向量.

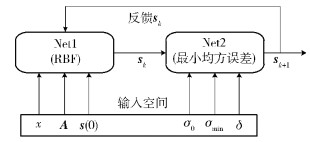
2 基于RBF网络的源信号恢复 2.1 RBF网络

下面介绍两层级联的RBF网络，如图 1所示，Net1由RBF构成，Net2为实现最小均方误差.

常用的RBF为高斯核函数，定义为

$ K\left( {\mathit{\boldsymbol{v}},\mathit{\boldsymbol{v'}}} \right) = \exp \left( { - \frac{{\left\| {\mathit{\boldsymbol{v}} - \mathit{\boldsymbol{v'}}} \right\|_2^2}}{{2{\sigma ^2}}}} \right) $

(3)

其中：v、v′为输入数据，σ > 0为自由参数. 图 1中的参数和式 (3) 中的参数在后文中依次介绍.下面引入稀疏恢复模型.原始的稀疏信号恢复模型如下：

$ \min {\left\| \mathit{\boldsymbol{s}} \right\|_{{\ell _0}}}{\rm{subject}} {\rm{to}} \mathit{\boldsymbol{x = As}} $

(4)

其中：s为待恢复的信号向量，x为观测向量，A为混合矩阵 (任意2个列向量之间不相关). ‖s‖_{${\ell _0}$}表示s的${\ell _0}$范数，即向量s中非零元素的个数.

根据压缩感知^[5]理论可知，式 (4) 属于NP-hard问题.因此需要对式 (4) 做进一步修改使其转化成可优化的问题，一个有效的方法是使用近似${\ell _0}$范数来替换式 (4) 中的‖s‖_{${\ell _0}$}.回到式 (3)，令s_i=‖v-v′‖₂，则式 (3) 变为K(v, v′)=K(s_i)=exp$\left( { - \frac{{s_i^2}}{{2{\sigma ^2}}}} \right)$.现在考虑如下模型：

$ \min {F_1}\left( \mathit{\boldsymbol{s}} \right) {\rm{subject}} {\rm{to}} \mathit{\boldsymbol{x = As}} $

(5)

其中F₁(s)=σ²$\left( {N - \sum\limits_{i = 1}^N {K\left( {{s_i}} \right)} } \right)$.显然，σ的值越小，F₁(s) 越能逼近向量s的${\ell _0}$范数，因此当σ取值足够小的时候，可以使用式 (5) 来近似代替式 (4).

在实际应用中，由于受到噪声的干扰，式 (4) 或者式 (5) 中的约束条件x=As不会严格成立，更为合理的约束条件应为‖x-As‖₂² < ε，ε为门限值，它与噪声强度有关.因此，图 1中的Net2(最小均方误差) 可以定义为

$ \min \frac{1}{2}\left\| {\mathit{\boldsymbol{x - As}}} \right\|_2^2 $

(6)

至此，图 1中的RBF网络已完成定义，输入空间由观测信号、混合矩阵和初始化参数构成.

为了使图 1中RBF网络的输出尽可能收敛至真实的源信号，实行交替优化，即式 (5) 的结果作为式 (6) 的输入，式 (6) 的结果作为式 (5) 的输入，因此在RBF网络中形成一个反馈回路，提高了源信号恢复的精度.

2.2 源信号恢复方法

对于Net1的优化，为了避免最速下降法所产生的“锯齿”效应的影响以及步长选取的问题，使用牛顿法进行迭代优化.首先计算F₁(s) 的梯度，可得

$ \nabla {F_1}\left( \mathit{\boldsymbol{s}} \right) = {\left[ {\frac{{{s_1}}}{{{\sigma ^2}}}{{\rm{e}}^{ - \frac{{s_1^2}}{{2{\sigma ^2}}}}},\frac{{{s_2}}}{{{\sigma ^2}}}{{\rm{e}}^{ - \frac{{s_2^2}}{{2{\sigma ^2}}}}}, \cdots ,\frac{{{s_N}}}{{{\sigma ^2}}}{{\rm{e}}^{ - \frac{{s_N^2}}{{2{\sigma ^2}}}}}} \right]^{\rm{T}}} $

(7)

求出式 (7) 对应的Hessen矩阵：

$ \begin{array}{*{20}{c}} {{\nabla ^2}{F_1}\left( \mathit{\boldsymbol{s}} \right) = }\\ {{\rm{diag}}\left[ {{{\rm{e}}^{ - \frac{{s_1^2}}{{2{\sigma ^2}}}}}\left( {\frac{{{\sigma ^2} - s_1^2}}{{{\sigma ^4}}}} \right),{{\rm{e}}^{ - \frac{{s_2^2}}{{2{\sigma ^2}}}}}\left( {\frac{{{\sigma ^2} - s_2^2}}{{{\sigma ^4}}}} \right), \cdots ,{{\rm{e}}^{ - \frac{{s_N^2}}{{2{\sigma ^2}}}}}\left( {\frac{{{\sigma ^2} - s_N^2}}{{{\sigma ^4}}}} \right)} \right]} \end{array} $

(8)

牛顿法和梯度下降法不同之处在于搜索方向的选取，牛顿方向为

$ \mathit{\boldsymbol{d = }} - {\left[ {{\nabla ^2}{F_1}\left( \mathit{\boldsymbol{s}} \right)} \right]^{ - 1}}\nabla {F_1}\left( \mathit{\boldsymbol{s}} \right) $

(9)

但牛顿方向不一定是F₁(s) 的下降方向，这就可能导致算法失效.

为保证牛顿方向d为F₁(s) 的下降方向，要求∇²F₁(s) 为正定矩阵，可以简单证明：令D=(∇F₁(s))^Td=-(∇F₁(s))^T[∇²F₁(s)]^-1∇F₁(s)，要使牛顿方向d为F₁(s) 的下降方向，D必须小于0，从而 (∇F₁(s))^T[∇²F₁(s)]^-1∇F₁(s)>0，这意味着∇²F₁(s) 为正定矩阵.

所以，需要对式 (9) 中的矩阵进行修正，使Hessen矩阵∇²F₁(s) 成为正定矩阵.修正后的Hessen矩阵为G=∇²F₁(s)+V(V∈$\mathbb{R}$^N×N为对角矩阵)，让G代替式 (9) 中的Hessen矩阵进行迭代搜索.为了使修正后的矩阵G为正定矩阵，可以取

$ \mathit{\boldsymbol{V = }}{\rm{diag}}\left[ {\frac{{2s_1^2}}{{{\sigma ^4}}}{{\rm{e}}^{ - \frac{{s_1^2}}{{2{\sigma ^2}}}}},\frac{{2s_2^2}}{{{\sigma ^4}}}{{\rm{e}}^{ - \frac{{s_2^2}}{{2{\sigma ^2}}}}}, \cdots ,\frac{{2s_N^2}}{{{\sigma ^4}}}{{\rm{e}}^{ - \frac{{s_N^2}}{{2{\sigma ^2}}}}}} \right] $

(10)

进一步可以得到

$ \mathit{\boldsymbol{G}} = {\rm{diag}}\left[ {\frac{{{\sigma ^2} + s_1^2}}{{{\sigma ^4}}}{{\rm{e}}^{ - \frac{{s_1^2}}{{2{\sigma ^2}}}}},\frac{{{\sigma ^2} + s_2^2}}{{{\sigma ^4}}}{{\rm{e}}^{ - \frac{{s_2^2}}{{2{\sigma ^2}}}}}, \cdots ,\frac{{{\sigma ^2} + s_N^2}}{{{\sigma ^4}}}{{\rm{e}}^{ - \frac{{s_N^2}}{{2{\sigma ^2}}}}}} \right] $

(11)

显然，矩阵G中的对角元素全部满足恒大于0，符合正定矩阵的条件.根据上面得到的修正的Hessen矩阵以及牛顿方程公式，可以求得修正后的牛顿方向：

$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{d = }} - {\mathit{\boldsymbol{G}}^{ - 1}}\nabla {F_1}\left( \mathit{\boldsymbol{s}} \right) = }\\ {{{\left[ { - \frac{{{\sigma ^2}{s_1}}}{{{\sigma ^2} + s_1^2}}, - \frac{{{\sigma ^2}{s_2}}}{{{\sigma ^2} + s_2^2}}, \cdots ,\frac{{{\sigma ^2}{s_N}}}{{{\sigma ^2} + s_N^2}}} \right]}^{\rm{T}}}} \end{array} $

(12)

利用修正后的牛顿方向作为算法的迭代方向，可以得到估计信号由第k次到第k+1次迭代的递推公式为

$ {\mathit{\boldsymbol{s}}_{k + 1}} = {\mathit{\boldsymbol{s}}_k} + {\mathit{\boldsymbol{d}}_k} $

(13)

其中d_k=${\left[{-\frac{{\sigma _k^2{s_1}}}{{\sigma _k^2 + s_1^2}} -\frac{{\sigma _k^2{s_2}}}{{\sigma _k^2 + s_2^2}} \cdots-\frac{{\sigma _k^2{s_N}}}{{\sigma _k^2 + s_N^2}}} \right]^{\text{T}}}$为了使F₁(s) 越来越逼近源信号向量s的${\ell _0}$范数，每次迭代选取一个σ值，且逐渐减小至门限值σ_min，即σ_min < σ_k+1 < σ_k.

对于Net2的优化，由于式 (6) 中的目标函数的Hessen矩阵不是对角阵，在进行矩阵求逆时计算较为复杂且精度很难保证，因此采用文献[3]中的迭代方法求解式 (6)，迭代公式为

$ {\mathit{\boldsymbol{s}}_{k + 1}} = {\mathit{\boldsymbol{s}}_k} + {\mu _j}\mathit{\boldsymbol{A}}_j^{\rm{T}}\left( {{x_j} - {\mathit{\boldsymbol{A}}_j}{\mathit{\boldsymbol{s}}_k}} \right), j = 1,2, \cdots ,M $

(14)

其中：μ_j=1/‖A_j‖₂为迭代步长，A_j为A的第j行.具体的推导过程可参考文献[3]，这里不再重复推导.

经过上述分析，使用式 (13) 和式 (14) 进行交替优化，即可在Net1和Net2之间形成反馈回路，使得RBF网络的输出尽可能收敛至真实的源信号.输入空间中的参数初始化如下：s_k的初始值为s₀=A^T(AA^T)^-1x，δ为小于1的尺度参数，在仿真实验中取值为0.6，用于更新σ. σ为式 (3) 中的自由参数，当取值较小时，Net1中的F₁(s) 越能够逼近向量s的${\ell _0}$范数，但是随着σ值的减小，F₁(s) 的平滑性越差，局部极值点越多.因此在进行交替优化的过程中，σ取值应当逐渐减小.在仿真实验中，σ初始化为σ₀=2max{s₀}，最小值为σ_min.

综上所述，基于RBF网络的欠定盲分离源信号恢复算法流程如下：

步骤1  初始化估计信号s₀=A^T(AA^T)^-1x，尺度参数δ=0.6，σ₀=2max{s₀}，σ_min=10^-5，迭代次数k=0.

步骤2  当σ_k > σ_min时，执行步骤3至步骤6.

步骤3  根据式 (12) 求出牛顿方向d_k.

步骤4  根据式 (13)，更新s_k：s_k←s_k+d_k.

步骤5  对于j=1, 2, …, M(M为观测信号个数)，执行1)、2)：

1) α_k=(x_j-A_js_k)/‖A_j‖₂，其中A_j为A的第j行；

2) 更新s_k：s_k←s_k+α_kA_j.

步骤6  σ_k+1=δσ_k，s_k+1=s_k，更新k：k←k+1.

步骤7  输出s_k.

3 算法的收敛性和复杂度分析

根据文献[6]，迭代产生的源信号序列{s_k}所循的路径呈现出“锯齿现象”，影响收敛速度.当Hessen矩阵∇²F₁(s) 条件数很大时，“锯齿现象”尤为严重.但是基于RBF网络的欠定盲分离源信号恢复 (SRRBF, source recovery in underdetermined blind source separation based on RBF network) 算法中所引入的牛顿法可以快速收敛，下面说明对Net1中F₁(s) 的优化可以实现至少2级收敛.根据文献[6]，有如下定理.

定理  设f(s) 为二次连续可微函数，$\mathit{\boldsymbol{\bar s}}$满足$\nabla f\left( {\mathit{\boldsymbol{\bar s}}} \right) = 0$，且${\nabla ^2}f\left( {\mathit{\boldsymbol{\bar s}}} \right)$可逆.当s′接近$\mathit{\boldsymbol{\bar s}}$时，使得存在k₁, k₂ > 0，满足k₁k₂ < 1，且对每一个$\mathit{\boldsymbol{s}} \in \mathit{\boldsymbol{S}} = \left\{ {\mathit{\boldsymbol{s}}|\left\| {\mathit{\boldsymbol{s}} - \mathit{\boldsymbol{\bar s}}} \right\| \leqslant \left\| {\mathit{\boldsymbol{s}}' - \mathit{\boldsymbol{\bar s}}} \right\|} \right\}$，有

$ \left\| {{\nabla ^2}f{{\left( {\mathit{\boldsymbol{\bar s}}} \right)}^{ - 1}}} \right\| \le {k_1} $

(15)

$ \frac{{\left\| {\nabla f\left( {\mathit{\boldsymbol{\bar s}}} \right) - \nabla f\left( \mathit{\boldsymbol{s}} \right) - {\nabla ^2}f\left( \mathit{\boldsymbol{s}} \right)\left( {\mathit{\boldsymbol{\bar s}} - \mathit{\boldsymbol{s}}} \right)} \right\|}}{{\left\| {\mathit{\boldsymbol{\bar s}} - \mathit{\boldsymbol{s}}} \right\|}} \le {k_2} $

(16)

则牛顿法产生的序列收敛于$\mathit{\boldsymbol{\bar s}}$.下面结合该定理做收敛性分析.

在Net1中F₁(s) 达到最优解的极值条件为$\nabla {F_1}\left( {\mathit{\boldsymbol{\bar s}}} \right) = \mathit{\boldsymbol{0}}, \mathit{\boldsymbol{\bar s}}$为最优解.令F₁(s)=f(s)，且对牛顿方向修正后，得到G=∇²F₁(s)+V.利用式 (10)、式 (15) 和式 (16) 做进一步的推导，可得到

$ \left\| {{\mathit{\boldsymbol{G}}^{ - 1}}} \right\| \le {{k'}_1} $

(17)

$ \frac{{\left\| {\nabla {F_1}\left( {\mathit{\boldsymbol{\bar s}}} \right) - \nabla f\left( \mathit{\boldsymbol{s}} \right) - \mathit{\boldsymbol{G}}\left( {\mathit{\boldsymbol{\bar s}} - \mathit{\boldsymbol{s}}} \right)} \right\|}}{{\left\| {\mathit{\boldsymbol{\bar s}} - \mathit{\boldsymbol{s}}} \right\|}} \le {{k'}_2} $

(18)

其中k′₁, k′₂>0，k′₁k′₂ < 1.当s_k∈S，s_k≠$\mathit{\boldsymbol{\bar s}}$时，有

$ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{s}}_{k + 1}} - \mathit{\boldsymbol{\bar s}} = {\mathit{\boldsymbol{s}}_k} - {\mathit{\boldsymbol{G}}^{ - 1}}\nabla {F_1}\left( {{\mathit{\boldsymbol{s}}_k}} \right) - \mathit{\boldsymbol{\bar s}} = }\\ {\left( {{\mathit{\boldsymbol{s}}_k} - \mathit{\boldsymbol{\bar s}}} \right) - {\mathit{\boldsymbol{G}}^{ - 1}}\left[ {\nabla {F_1}\left( {{\mathit{\boldsymbol{s}}_k}} \right) - \nabla {F_1}\left( {\mathit{\boldsymbol{\bar s}}} \right)} \right] = }\\ {{\mathit{\boldsymbol{G}}^{ - 1}}\left[ {\nabla {F_1}\left( {\mathit{\boldsymbol{\bar s}}} \right) - \nabla {F_1}\left( {{\mathit{\boldsymbol{s}}_k}} \right) - \mathit{\boldsymbol{G}}\left( {\mathit{\boldsymbol{\bar s}} - {\mathit{\boldsymbol{s}}_k}} \right)} \right]} \end{array} $

(19)

再考虑到式 (17) 和式 (18)，有

$ \begin{array}{*{20}{c}} {\left\| {{\mathit{\boldsymbol{s}}_{k + 1}} - \mathit{\boldsymbol{\bar s}}} \right\| \le }\\ {\left\| {{\mathit{\boldsymbol{G}}^{ - 1}}} \right\|\left\| {\nabla {F_1}\left( {\mathit{\boldsymbol{\bar s}}} \right) - \nabla {F_1}\left( {{\mathit{\boldsymbol{s}}_k}} \right) - \mathit{\boldsymbol{G}}\left( {\mathit{\boldsymbol{\bar s}} - {\mathit{\boldsymbol{s}}_k}} \right)} \right\| \le }\\ {{{k'}_1}{{k'}_2}\left\| {{\mathit{\boldsymbol{s}}_k} - \mathit{\boldsymbol{\bar s}}} \right\| < \left\| {{\mathit{\boldsymbol{s}}_k} - \mathit{\boldsymbol{\bar s}}} \right\|} \end{array} $

(20)

因此，s_k+1比s_k更接近于$\mathit{\boldsymbol{\bar s}}$，即序列{s_k}收敛于$\mathit{\boldsymbol{\bar s}}$.实际上，在收敛时有下列关系：

$ \left\| {{\mathit{\boldsymbol{s}}_{k + 1}} - \mathit{\boldsymbol{\bar s}}} \right\| \le c{\left\| {{\mathit{\boldsymbol{s}}_k} - \mathit{\boldsymbol{\bar s}}} \right\|^2} $

(21)

其中：$\mathit{\boldsymbol{\bar s}}$为源信号的最优解，c为某个常数.利用极值条件、泰勒定理及相应矩阵运算可推导出式 (21)，由于篇幅的限制，这里不做具体的推导.由式 (21) 知修正的牛顿法至少2级收敛，可见修正的牛顿法的收敛速度比较快.

对于SRRBF算法而言，计算复杂度主要来源于式 (13)、式 (14) 以及步骤5，因此，若算法迭代次数为L₁，加法和乘法的次数分别约为L₁[2N+(3T)^M]和L₁[4N+(3T+1)^M].对于RASR算法，计算复杂度主要来自于梯度的计算和迭代点的更新，若迭代次数为L₂，则加法和乘法的次数分别约为L₂[2T-1+(3T)^M]和L₂[T+1+(3T+1)^M].一般而言，源信号数目N远小于采样点数目T，由于修正的牛顿法收敛速度更快，使得${L_1} \ll {L_2}$，所以SRRBF算法的复杂度明显小于RASR算法.对SL0、RSL0、HOSL0算法可做类似的分析，限于篇幅不再具体分析.

4 算法仿真与结果分析

为了比较提出的SRRBF算法与现有的基于${\ell _0}$范数的算法的性能，对SL0、RSL0、RASR、HOSL0以及SRRBF这5种算法进行仿真.在仿真实验中产生5路稀疏源信号，混合矩阵A为3行5列的高斯随机矩阵.稀疏度表示在某一时刻每路源信号为0的概率.信号采样长度T=1 000.实验中采用运算时间来衡量算法复杂度，使用相关系数来衡量算法的精度，其中源信号与恢复信号的相关系数定义为

$ {\gamma _{{\rm{coef}}}}\left( {\mathit{\boldsymbol{\hat S}},\mathit{\boldsymbol{S}}} \right) = \frac{1}{N}\sum\limits_{n = 1}^N {\frac{{\left| {\sum\limits_{t = 1}^T {s\left( {n,t} \right)\hat s\left( {n,t} \right)} } \right|}}{{\sqrt {\sum\limits_{t = 1}^T {{s^2}\left( {n,t} \right)} \sum\limits_{t = 1}^N {{{\hat s}^2}\left( {n,t} \right)} } }}} $

(22)

其中：S为估计得到的源信号，$\mathit{\boldsymbol{\hat S}}$为实际的源信号，s(n, t) 为S的第n行第t列个元素，$\hat s\left( {n, t} \right)$为$\mathit{\boldsymbol{\hat S}}$的第n行第t列个元素.相关系数越大，表示精度越高.相关系数的最大值为1.

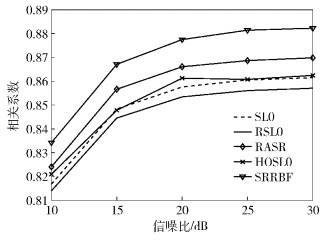
根据图 2可知，在稀疏度为0.8的情况下，在信噪比从10~30 dB变化范围内，SRRBF算法的相关系数均大于其他4种算法.比如，在10 dB的情况下，SRRBF算法的相关系数分别比SL0、RSL0、RASR、HOSL0算法高出了约2.13%、2.49%、1.20%、1.62%.

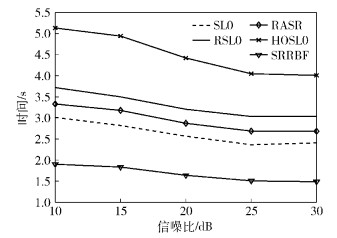
由图 3可得，在稀疏度为0.8的情况下，在信噪比从10~30 dB变化范围内，SRRBF算法的运算时间小于其他4种算法.比如，在10 dB的情况下，SRRBF算法运行时间分别比SL0、RSL0、RASR、HOSL0算法降低了约36.82%、48.83%、42.85%、62.92%.

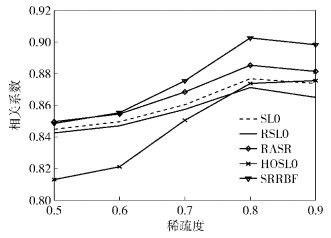
图 4给出了信噪比为10 dB情况下5种算法相关系数随稀疏度变化的曲线.由图 4可以看出，当稀疏度小于0.55时，SRRBF算法的相关系数大于SL0、RSL0、HOSL0算法，略微小于RASR算法.例如，稀疏度为0.5的情况下，SRRBF算法的相关系数比RASR算法减小了约0.1%，而比SL0、RSL0、HOSL0算法分别提高了约0.4%、0.7%、4.3%.当稀疏度大于0.55时，SRRBF算法的相关系数均大于其他4种算法.

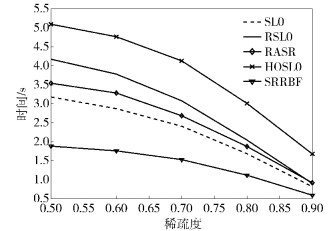
由图 5可以看出，SRRBF算法的运算复杂度显著小于其他4种算法.比如，在稀疏度为0.5的条件下，SRRBF算法比SL0、RSL0、RASR、HOSL0算法的运行时间分别降低了约40.75%、54.88%、46.82%、63.03%.

根据以上的仿真结果及分析可以得出：1) 在信号稀疏度较小的情况下，与RASR算法相比，SRRBF算法以牺牲极小的精度作为代价，节约了大量的运算时间，即同时兼顾了复杂度和精度；2) 在源信号稀疏度较大的情况下，SRRBF算法在复杂度和精度方面均优于SL0、RSL0、RASR、HOSL0算法.

5 结束语

针对现有的基于优化近似${\ell _0}$范数算法收敛速度慢，精度受步长影响较大的问题，提出了SRRBF算法.该算法在RBF网络的基础上，实行交替优化，同时引入修正的牛顿法克服算法精度受步长影响的缺点.与现有的SL0、RSL0、RASR、HOSL0算法相比，SRRBF算法在保证有较高恢复精度的同时，显著减少了算法的时间复杂度，在处理欠定盲分离源信号恢复问题时具有明显的优势.