近年来，干扰对齐 (IA，interference alignment) 作为一种新型干扰管理技术得到了广泛的关注. IA的主要思想是通过在发送端进行合理的预编码，使得在接收端将所有干扰信号压缩到相同的子空间，从而为期望信号提供无干扰的信号维度进行数据传输.该技术实现的前提是发送端必须获知完美的全局信道状态信息 (CSI，channel state information).在实际的频分双工通信系统中，发送端必须通过信道训练和反馈来获得全局CSI^[1]，而信道训练和反馈过程中不可避免地存在一定的信道估计误差，因此完美的CSI不可能获得，这使得IA的性能受到严重的影响.基于有限量化反馈机制，Chen等^[2]通过合理分配各用户的反馈比特数优化了IA的性能；Ayach等^[3]提出了模拟反馈机制：不同于量化反馈，接收端直接把CSI信息以模拟信号的方式广播出去而无须量化编码，有效地降低了反馈开销.然而现有文献对IA的分析都假设信道是静态的，并未考虑信道的时变特性.

笔者基于模拟反馈机制中发送端所获得的信道状态信息表达式推导了由于噪声和信道时变特性共同导致的CSI估计误差，仿真了在任意信噪比 (SNR，signal noise ratio) 条件下CSI误差对IA系统和速率的影响；笔者还提出了一种基于卡尔曼预测的CSI修正方法，降低了CSI估计误差，提升了IA性能.

1 系统模型

考虑典型的K用户干扰信道.所有发送端和接收端均配置相同的天线数，假设为M.每个发送端给对应的接收端发送d个数据流，且d满足IA的可行性条件，即d≤2M/(K+1) ^[4].在时刻t，接收端j接收到的信号表达式为

$ {\mathit{\boldsymbol{Y}}_j}\left( t \right) = \sum\limits_{i = 1}^K {\sqrt {\frac{{{P_f}}}{d}} } {\mathit{\boldsymbol{h}}_{i,j}}\left( t \right){\mathit{\boldsymbol{V}}_i}{\mathit{\boldsymbol{s}}_i} + {\mathit{\boldsymbol{n}}_j}\left( t \right) $

(1)

其中：h_{j, i}(t)∈$\mathbb{C}$^M×M为t时刻发送端i和接收端j之间的信道矩阵；V_i=[v_{i, 1}, …, v_{i, d}]∈$\mathbb{C}$^M×d为发送端i的预编码矩阵；s_i∈$\mathbb{C}$^d×1为发送端i的发送信号向量，且满足E(s_is_i^H)=I_d；n_j(t)∈$\mathbb{C}$^M×1为t时刻接收端的噪声，其每个元素是独立同分布的均值为0、方差为σ²的高斯随机变量；另外，P_f为发送端的发射功率.为简便起见，下面部分表达式的书写省略了时刻t，如h_{j, i}(t) 写为h_{j, i}，表示任意时刻的信道增益矩阵.

系统和速率可表示为

$ {R_{{\rm{sum}}}} = \sum\limits_{i = 1}^K {\sum\limits_{s = 1}^d {{\rm{lb}}\left( {1 + \frac{{\frac{{{P_f}}}{d}{{\left| {\mathit{\boldsymbol{u}}_{j,s}^{\rm{H}}{\mathit{\boldsymbol{h}}_{j,j}}{\mathit{\boldsymbol{v}}_{j,s}}} \right|}^2}}}{{{J_{j,s}} + {\sigma ^2}}}} \right)} } $

(2)

其中：u_{j, s}为接收端j的干扰抑制矩阵U_j的第s列，U_j=[u_{j, 1}, …, u_{j, d}]∈$\mathbb{C}$^M×d；J_{j, s}为接收端j在第s个数据流上收到的干扰信号.只有当发送端获得完美的CSI时，接收端的干扰才能被完全消除，即J_{j, s}=0；否则就会产生干扰泄露.

为了便于描述信道增益随时间的变化关系，考虑经典的1阶高斯-马尔可夫时变信道模型^[5].发送天线m到接收天线n的信道在时刻l和l-k之间的时域相关函数可表示为信道增益积的期望，即r_{l, l-k}(m, n)=E(h_{m, n}(l)h_{m, n}(l-k)^H)，并作如下2个假设.

假设1  r_{l, l-k}(m, n)=r_k(m, n)，即信道是时间平稳的，且相关函数在所有发送端都是已知的.

假设2  不同天线对的信道相关函数是均匀同一的，即r_k(m, n)=r_k.

根据以上假设，只讨论信道矩阵h(k) 中任意元素h(k).根据1阶高斯-马尔可夫信道模型，信道增益的变化规律可表示为

$ h\left( k \right) = rh\left( {k - 1} \right) + \sqrt {1 - {r^2}} \varphi \left( k \right) $

(3)

其中：r为信道在2个相邻时刻间的时域相关函数；φ(k) 是服从均值为0，方差为1的高斯分布的随机噪声.

2 基于模拟反馈的CSI估计误差

在频分双工系统中，信道不具有互易性，上下行信道相互独立，发送端的CSI估计过程主要分为前向信道训练、反向信道训练和CSI反馈.基于文献[3]中的模拟反馈方式，推导了由于噪声和信道时变特性共同导致的CSI估计误差，具体步骤如下.

1) 前向和反向信道训练

首先，每个发送端i广播一个M×N_ft的导频序列Φ_i满足正交性Φ_iΦ_k^H=δ_ikI_M，其中N_ft=KM.接收端j根据收到的信号Y_j计算出前向信道矩阵h_{j, i}的最小均方误差估计 (MMSE，minimum mean error estimation) 值${\boldsymbol{\hat h}_{j, i}}$. ${\boldsymbol{\hat h}_{j, i}}$中每个元素服从均值为0，方差为$\frac{{{N_{ft}}{P_f}/M}}{{{\sigma ^2} + {N_{ft}}{P_f}/M}}$的高斯分布；相应的信道估计误差矩阵${{\mathit{\boldsymbol{\tilde h}}}_{j, i}} = {\mathit{\boldsymbol{h}}_{j, i}} - {{\mathit{\boldsymbol{\hat h}}}_{j, i}}$中的元素服从均值为0，方差为$\frac{{{\sigma ^2}}}{{{\sigma ^2} + {N_{ft}}{P_f}/M}}$的高斯分布.

同理执行反向信道训练，每个接收端广播一个M×N_rt的导频序列Θ_j满足正交性Θ_jΘ_k^H=δ_jkI_M，其中N_rt=KM.发送端计算反向信道的估计值${{\mathit{\boldsymbol{\hat g}}}_{j, i}}$.相应的信道估计误差矩阵${{\mathit{\boldsymbol{\tilde g}}}_{j, i}}\mathit{\boldsymbol{ = }}{\mathit{\boldsymbol{g}}_{\mathit{j, i}}} - {{\mathit{\boldsymbol{\hat g}}}_{j, i}}$中元素服从均值为0，方差为$\frac{{{\sigma ^2}}}{{{\sigma ^2} + {N_{rt}}{P_{\text{r}}}/M}}$的高斯分布.其中P_r为接收端的发射功率.

2) CSI模拟反馈

在进行了前向和反向信道训练之后，各接收端将其在步骤1) 中估计的前向信道信息在N_fb=K²M个符号内反馈回发送端.发送端i接收信号表达式为

$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{Y}}_i^ * = \sqrt {\frac{{{N_{fb}}{P_r}}}{{K{M^2}}}{{\left( {\frac{{{N_{fr}}{P_f}/M}}{{{\sigma ^2} + {N_{fr}}{P_f}/M}}} \right)}^{ - 1}}} \times }\\ {\sum\limits_{j = 1}^K {\mathit{\boldsymbol{g}}_{j,i}^ * \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat h}}}_{j,1}}} & \cdots & {{{\mathit{\boldsymbol{\hat h}}}_{j,K}}} \end{array}} \right]{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_j} + \mathit{\boldsymbol{n}}_i^ * } } \end{array} $

(4)

其中：$\mathit{\boldsymbol{g}}_{j, i}^*$为反馈过程中的实际反向信道矩阵，由于信道的时变性，$\mathit{\boldsymbol{g}}_{j, i}^*$并不等于g_{j, i}；Ψ_j为KM×N_fb的单位扩展矩阵，满足Ψ_kΨ_j^H=δ_kjI_KM.发送端对反馈回来的信息作MMSE估计得到最终的CSI估计值，表达式如式 (5) 所示.

$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat h}}_i^ * = \sqrt {\frac{{K{M^2}}}{{{N_{fb}}{P_r}}}\frac{{{N_{fr}}{P_f}/M}}{{{\sigma ^2} + {N_{fr}}{P_f}/M}}} {{\left( {\mathit{\boldsymbol{\hat g}}_{j,i}^{\rm{H}}{{\mathit{\boldsymbol{\hat g}}}_{j,i}}} \right)}^{ - 1}}\mathit{\boldsymbol{\hat g}}_{j,i}^{\rm{H}}\mathit{\boldsymbol{Y}}_i^ * \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_j^{\rm{H}} = }\\ {\mathit{\boldsymbol{\hat g}}_{j,i}^{ - 1}\mathit{\boldsymbol{g}}_{j,i}^ * {{\mathit{\boldsymbol{\hat h}}}_j} + \sqrt {\frac{{K{M^2}}}{{{N_{fb}}{P_r}}}\frac{{{N_{fr}}{P_f}/M}}{{{\sigma ^2} + {N_{fr}}{P_f}/M}}} \mathit{\boldsymbol{\hat g}}_{j,i}^{ - 1}\mathit{\boldsymbol{n}}_i^ * \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_j^{\rm{H}} = }\\ {{{\left[ {{L_3}\left( {{r_m}\mathit{\boldsymbol{g}}_{j,i}^ * + \sqrt {1 - r_m^2} \mathit{\boldsymbol{\lambda }}} \right) + {L_4}{\mathit{\boldsymbol{n}}_j}\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_i^{\rm{H}}} \right]}^{ - 1}} \times }\\ {\left\{ {\mathit{\boldsymbol{g}}_{j,i}^ * \left[ {{L_1}\left( {{r_n}\mathit{\boldsymbol{h}}_{j,i}^ * + \sqrt {1 - r_n^2} \mathit{\boldsymbol{\varphi }}} \right) + {L_2}{\mathit{\boldsymbol{n}}_j}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_i^{\rm{H}}} \right] + {L_5}\mathit{\boldsymbol{n}}_i^ * \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_j^{\rm{H}}} \right\}} \end{array} $

(5)

其中：${r_m} = {r^{{N_{fb}}}}, {\mathit{\boldsymbol{g}}_{j, i}} = {r_m}\mathit{\boldsymbol{g}}_{j, i}^* + \sqrt {1 - r_m^2} \mathit{\boldsymbol{\lambda }}, {r_n} = {r^{{N_{fb}} + {N_{rt}}}}$，

$ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{h}}_{j,i}} = {r_n}\mathit{\boldsymbol{h}}_{j,i}^ * + \sqrt {1 - r_n^2} \mathit{\boldsymbol{\varphi }},\mathit{\boldsymbol{\lambda }} \sim {\rm{CN}}\left( {0,{\mathit{\boldsymbol{I}}_M}} \right),}\\ {\mathit{\boldsymbol{\varphi }} \sim {\rm{CN}}\left( {0,{\mathit{\boldsymbol{I}}_M}} \right),{L_1} = \frac{{{N_{fr}}{P_f}/M}}{{{\sigma ^2} + {N_{fr}}{P_f}/M}},{L_2} = \frac{{\sqrt {{N_{fr}}{P_f}/M} }}{{{\sigma ^2} + {N_{fr}}{P_f}/M}},}\\ {{L_3} = \frac{{{N_{rt}}{P_r}/M}}{{{\sigma ^2} + {N_{rt}}{P_r}/M}},{L_2} = \frac{{\sqrt {{N_{rt}}{P_r}/M} }}{{{\sigma ^2} + {N_{rt}}{P_r}/M}},}\\ {{L_5} = \frac{{K{M^2}}}{{{N_{fb}}{P_r}}}\frac{{{N_{fr}}{P_f}/M}}{{{\sigma ^2} + {N_{fr}}{P_f}/M}}} \end{array} $

发送端最终得到CSI估计值的均方误差为

$ \begin{array}{*{20}{c}} {\sigma _{\mathit{\boldsymbol{h}}_j^ * }^2 = E\left\{ {\left( {\mathit{\boldsymbol{h}}_j^ * - \mathit{\boldsymbol{\hat h}}_j^ * } \right){{\left( {\mathit{\boldsymbol{h}}_j^ * - \mathit{\boldsymbol{\hat h}}_j^ * } \right)}^{\rm{H}}}} \right\} = }\\ {{L_1}\left( {r_m^2 - 2{r_m}{r_n}} \right) + \frac{{{L_1} - {L_1}{L_3}r_m^2 + {L_5}{\sigma ^2}}}{{{L_3}M\left( {K - 1} \right)}} + 1} \end{array} $

(6)

该误差是由收发端的噪声和信道的时变共同导致的.信道的估计值表达式可近似简化为$\mathit{\boldsymbol{\hat h}}_i^* = \mathit{\boldsymbol{h}}_i^* + \sqrt {\sigma _{h_j^*}^2} \xi$.其中，ξ~CN (0, I_M).

由于信道的时变特征，这样的训练与反馈过程必须每隔T个符号执行1次，以更新当前的信道状态信息.每次CSI获取过程占用N_b个符号，N_b=N_ft+N_rt+N_fb.式 (6) 表明，在低SNR条件下，CSI估计误差较大，因此需要设计一种修正方法来降低CSI的估计误差，提升IA的性能.

3 基于卡尔曼预测的CSI修正方法

卡尔曼滤波是一个“最优化自回归数据处理算法”，它是在线性最小方差估计的基础上的数学结构比较简单的最优线性递推滤波方法^[6].卡尔曼滤波的实质是用上一个状态和当前状态的测量值来估计当前状态.不同时刻间的信道具有相关性，因此发送端可借助卡尔曼滤波，利用前一时刻的信息来预测当前时刻的CSI，再结合通过上文所述的基于信道训练和模拟反馈得到的CSI，推导出当前时刻修正后的CSI，具体步骤如下.

首先，确定信道的实际状态转移方程为

$ h\left( {kT} \right) = {r_T}h\left( {\left( {k - 1} \right)T} \right) + \sqrt {1 - r_T^2} \varphi \left( {kT} \right) $

(7)

以及由上文推导得到的估计方程为

$ \mathit{\boldsymbol{\hat h}}\left( {kT} \right) = h\left( {kT} \right) + \sqrt {\sigma _{\mathit{\boldsymbol{h}}_j^ * }^2} \omega \left( {kT} \right) $

(8)

其中：r_T=r^T，ω(kT)~CN (0, 1).然后，根据卡尔曼迭代过程计算出修正值，算法如下.

输入：r_T，$\sigma _{h_j^*}^2$，a，$\mathit{\boldsymbol{\hat h}}\left( {kT} \right)$，N；

输出：p(N)，S(NT)；

初始化：$p\left( 0 \right) = {R_v}, S\left( 0 \right) = \mathit{\boldsymbol{\hat h}}\left( 0 \right)$；

① for k=1:N

② p₁(k)=a²p(k-1)+R_w；

③ b(k)=p₁(k)/[p₁(k)+R_v]；

④ S(kT)=a[1-b(k)]S((k-1)T)+b(k) $\hat S\left( {kT} \right)$；

⑤ p(k)=p₁(k)[1-b(k)]；

⑥ end for

其中：Rw=1-rT2, Rv=σhj*2, a=rT.

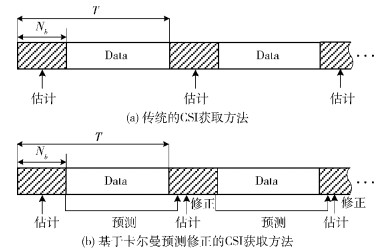
以上算法中，k为迭代次数，p₁(k) 为预测误差，b(k) 为卡尔曼增益，S(kT) 为第k次滤波后的信道增益值，p(k) 为第k次滤波后信道增益值和实际信道增益值间的均方误差值. 图 1所示为传统方法和基于卡尔曼预测修正方法的执行过程.

信道的变化规律是时间平稳的，即R_w和R_v为定值，因此该卡尔曼迭代过程具有收敛性^[6].令p(k)=p(k-1)=q，得

$ {a^2}{q^2} + \left( {{R_w} + {R_v} - {a^2}{R_v}} \right)q - {R_w}{R_v} = 0 $

(9)

解得q，即为均方误差的最终收敛值.再设函数

$ Q\left( x \right) = {a^2}{x^2} + \left( {{R_w} + {R_v} - {a^2}{R_v}} \right)x - {R_w}{R_v} $

将p(1)=R_v代入函数，得Q(R_v)=R_v²>0，由抛物线性质可知，q < R_v，即卡尔曼迭代过程降低了信道增益估计值的均方误差.以上证明了卡尔曼预测的有效性.

4 仿真分析

通过Matlab对所提方法进行仿真，并分析其性能.在仿真过程中，考虑了3用户干扰信道.发送端和接收端都配置有2根天线，每个发送端发送1个数据流.根据3GPP LTE标准^[7]，取正交频分复用 (OFDM，orthogonal frequency division multiplexing) 符号周期T_s=66.7 μs.相邻时刻信道间的相关系数用Clarke-Jakes模型描述为r=J₀(2πf_mT_s)，其中J₀(·) 为零阶第1类贝塞尔函数，f_m为多普勒频移.

设T个符号为1帧，每隔1帧执行1次CSI获取过程. 图 2所示为每一帧开始传输数据时信道增益的实际值、估计值和修正值的对比.第1个实际值依据均值为0、方差为1的高斯分布随机产生，之后的实际值依据式 (7) 产生. SNR记为α，仿真中取T=140，β=1，α=20 dB，f_m=30 Hz.传输载频为2.4 GHz，多普勒频移f_m=30 Hz相当于接收端以13.5 km/h的相对速度远离发送端.仿真结果显示，得益于卡尔曼预测算法的增益，信道增益的修正值比估计值更接近于实际值，具有更高的精确度.

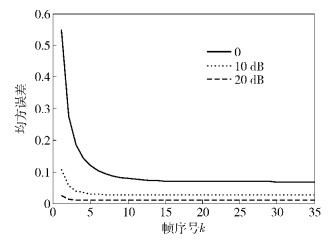
在不同SNR条件下，信道增益修正值的均方误差随时间变化如图 3所示.每2帧之间经历的时间为T×T_s.仿真中取T=140，β=1，f_m=30 Hz.仿真结果显示，α=0时，经过27帧的迭代卡尔曼预测达到收敛，均方误差值从0.549 9降至0.070 1；α=10 dB时，经过11帧的迭代卡尔曼预测达到收敛，均方误差值从0.108 1降至0.029 1；α=20 dB时，经过6帧迭代卡尔曼预测算法达到收敛，均方误差值从0.026 8降至0.012 5.可见，SNR越低，卡尔曼预测的收敛速度越慢，但对于信道增益的修正效果越明显.

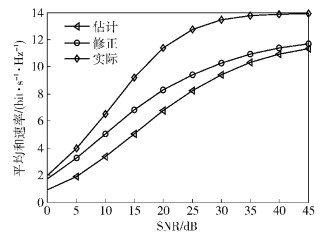
在不同的SNR条件下，对比了3种情况下的IA系统平均和速率：拥有完美CSI、通过传统方法获取CSI、经过卡尔曼预测修正法后获取CSI，分别对应于和速率的实际值、估计值和修正值如图 4所示.系统平均和速率定义为${{\bar R}_{{\text{sum}}}} = \frac{1}{T}\sum\limits_{t = {N_b} + 1}^T {{R_{{\text{sum}}}}\left( t \right)} $.仿真中取T=140，β=1，f_m=20 Hz.仿真结果显示，在相同的SNR条件下，系统和速率的实际值最大，而估计值最小，但在低SNR区域，修正值的性能逼近于实际值.随着SNR的增加，3种情况的平均和速率均有提高，但估计值与修正值之间的差距越来越小.原因是SNR较大时，噪声的影响可忽略不计，估计值已经具有足够高的精确度.

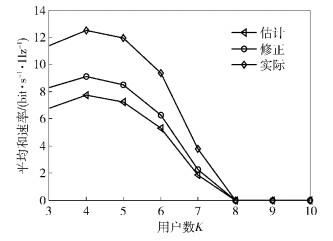
在上述3种情况下，图 5描述了IA系统平均和速率与用户数的对应关系.仿真取T=140，β=1，α=20 dB，f_m=30 Hz.仿真结果显示，修正值高于估计值而低于实际值，该结果与图 4一致. 图 5中3条曲线都随着用户数的增加先上升后下降，这主要是由于用户数的增加给系统带来容量增益的同时，也带来了巨大的导频开销，压缩了有效数据的传输时间，这二者间存在折中关系.值得注意的是，用户数超过8时，系统平均和速率降为0，这是由于导频开销超出了帧长，数据得不到传输机会，此时应重新设计可行的IA方案.

5 结束语

在综合考虑K用户干扰信道中的高斯随机噪声和多普勒频移的基础上，分析了模拟反馈机制中发送端获得的信道状态信息表达式及其误差.同时考虑信道的时间相关特性，引入基于卡尔曼预测的CSI修正方法，在不额外增加系统开销的前提下，有效地提升了CSI的精确度，抑制了由噪声和信道时变造成的IA性能损失.仿真对比了实际、估计和修正的信道增益值以及各自对应的系统平均和速率.结果表明，经过卡尔曼预测修正的IA性能明显优于使用传统CSI获取方法的IA性能，且在低SNR区域逼近拥有完美CSI的性能上界.