2. 中山大学 数据科学与计算机学院, 广州 510006
提出了一种应用于跨年龄人脸识别的联合学习方法,该方法由深度卷积神经网络构建而成,能在特征学习的同时学习到最优的测度函数,从而避免不合适的固定阈值所带来的匹配错误。针对有限的内存、过拟合和计算复杂性高的问题,在模型训练过程中采用了多种新颖和有效的训练策略。实验证实了该联合学习方法的有效性,在公开数据库MORPH-Ⅱ上的识别正确率达到了93.6%。
2. School of Data and Computer Science, Sun Yat-sen University, Guangzhou 510006, China
A joint learning approach (JLA) based on deep convolutional neural network (CNN) for age-invariant face verification was proposed. Feature representation, distance metric and decision function can be learned simultaneously thereafter. Comparing with traditional approaches, it uses fix threshold, so the match errors caused by unfit threshold can be avoided. Some strategies to overcome insufficient memory capacity, prevent over-fitting and reduce computational cost were also introduced. Experiment demonstrates the effectiveness of this approach; the rank-1 recognition accuracy is improved to 93.6% on the MORPH-Ⅱ database.
随着年龄的增长,人的容貌变化较大,而不同年龄段的变化特点也有所不同:从出生到成年,最大的变化是颅面变化,这种头部轮廓的变化是形状的变化;而从成年到老年,可观察到的变化就是皮肤的逐渐老化,是面部纹理的变化.同一个体的这些变化称为类内差异性.不同人在相近的年龄段有可能看起来比较相似,称为类间相似性.除了受类间相似性和类内差异性的影响外,人脸图像还受光照、表情、姿态、发型等诸多因素的影响,因此,跨年龄人脸识别问题非常具有挑战性.
1 相关研究近年来,跨年龄人脸识别问题引起了越来越多学者的关注. Li等[1]提出多特征区分分析法 (MFDA,multi-feature discriminant analysis);Gong等[2]提出潜在因素分析法 (HFA,hidden factor analysis);Chen等[3]提出了一种称为跨年龄引用编码法 (CARC,cross-age reference coding) 的数据驱动方法;Gong等[4]在HFA的基础上,进一步设计了最大熵特征描述子 (MEFD,maximum entropy feature descriptor),并采用身份因素分析匹配法 (IFA,identity factor analysis) 进行跨年龄人脸识别.最近,Li等[5]提出了一种新的层次学习模型法,并采用局部特征选择描述子 (LPS,local pattern selection) 进行跨年龄人脸识别.
以上方法中特征提取、特征变换和匹配识别各阶段都是独立进行的.实际上,特征提取和匹配识别之间是相互影响的,采用的特征不同,匹配的效果也会有所不同.如果构建特征和匹配联合学习的模型,提取最符合目标要求的特征,势必会提高匹配的效果.传统手工设计的特征很难达到这样的要求,而目前流行的深度卷积神经网络 (CNN,convolutional neural network) 可较为方便地构建高效的“端到端”的联合学习框架.深度卷积神经网络法已经在诸多计算机视觉任务,如图像分类、物体检测、语义分割中都取得了良好的效果,但目前还没有将基于CNN的联合学习模型应用于跨年龄识别的任务中.为了能在特征学习的同时学习到最优的测度函数,提出一种基于CNN的特征学习和距离测度学习的联合学习方法 (JLA,joint learning approach),并将其应用到跨年龄的人脸识别研究中.
2 距离测度学习及优化目标Xing等[6]首次提出马氏距离形式的距离测度学习算法.假设x和y分别为图像对 (x, y) 的特征向量,马氏距离为d(x, y)=(x-y)TM(x-y),其中M为半正定矩阵.距离测度学习方法一般通过相似样本对和不相似样本对的监督信息来学习马氏距离的参数矩阵M.在匹配阶段通常需要一个固定阈值d来确定x和y是否匹配,如果距离小于或等于阈值d,则匹配;否则,不匹配,可公式化为
| $ {\left( {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{y}}} \right)^{\rm T}}\mathit{\boldsymbol{M}}\left( {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{y}}} \right) \le d, \mathit{\boldsymbol{M}} \ge 0 $ | (1) |
然而,现实中很难确定一个合适的固定阈值,Li等[7]提出学习一个自适应的阈值函数d,d为关于 (x, y) 的函数,而不是固定阈值,从而避免由阈值不合适引起的判定错误.由此,式 (1) 变为 (x-y)T×M(x-y)≤d(x, y),而匹配问题的判定函数可写为
| $ \begin{array}{*{20}{c}} {f\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}}} \right) = d\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}}} \right) - }\\ {{{\left( {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{y}}} \right)}^{\rm T}}\mathit{\boldsymbol{M}}\left( {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{y}}} \right)\left\{ \begin{array}{l} \ge 0, 若 l\left( \mathit{\boldsymbol{x}} \right) = l\left( \mathit{\boldsymbol{y}} \right)\\ < 0, 其他 \end{array} \right.} \end{array} $ | (2) |
其中:l(x) 和l(y) 分别为图像x和y的类别标签,l(x)=l(y) 表示x和y为同一类. M本身是二次的,假设d(x, y) 为简单的二次型,有
| $ d\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}}} \right) = \frac{1}{2}{\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{\tilde Ax + }}\frac{1}{2}{\mathit{\boldsymbol{y}}^{\rm{T}}}\mathit{\boldsymbol{\tilde Ay + }}\frac{1}{2}{\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{\tilde By + }}{\mathit{\boldsymbol{c}}^{\rm{T}}}\left( {\mathit{\boldsymbol{x}} + \mathit{\boldsymbol{y}}} \right) + b $ |
代入式 (2) 可得
| $ f\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}}} \right) = \frac{1}{2}{\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{Ax + }}\frac{1}{2}{\mathit{\boldsymbol{y}}^{\rm{T}}}\mathit{\boldsymbol{Ay + }}{\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{By + }}{\mathit{\boldsymbol{c}}^{\rm{T}}}\left( {\mathit{\boldsymbol{x}} + \mathit{\boldsymbol{y}}} \right) + b $ | (3) |
其中:
| $ \begin{array}{*{20}{c}} {f\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}}} \right) = \frac{1}{2}{{\left( {{\mathit{\boldsymbol{L}}_\mathit{\boldsymbol{A}}}\mathit{\boldsymbol{x}}} \right)}^{\rm{T}}}\left( {{\mathit{\boldsymbol{L}}_\mathit{\boldsymbol{A}}}\mathit{\boldsymbol{x}}} \right) + \frac{1}{2}{{\left( {{\mathit{\boldsymbol{L}}_\mathit{\boldsymbol{A}}}\mathit{\boldsymbol{y}}} \right)}^{\rm{T}}}\left( {{\mathit{\boldsymbol{L}}_\mathit{\boldsymbol{A}}}\mathit{\boldsymbol{y}}} \right) - }\\ {{{\left( {{\mathit{\boldsymbol{L}}_\mathit{\boldsymbol{B}}}\mathit{\boldsymbol{x}}} \right)}^{\rm{T}}}\left( {{\mathit{\boldsymbol{L}}_\mathit{\boldsymbol{B}}}\mathit{\boldsymbol{y}}} \right) + {\mathit{\boldsymbol{c}}^{\rm{T}}}\mathit{\boldsymbol{x + }}{\mathit{\boldsymbol{c}}^{\rm{T}}}\mathit{\boldsymbol{y + }}b} \end{array} $ | (4) |
经过以上分析,通过有监督训练学习到矩阵LA、LB和向量c后,运用式 (4) 就可确定图像的匹配问题.跨年龄人脸识别问题的目标为:对于人物P的某年龄实例z,学习一个重识别的模型从而能正确地识别P的另一个年龄实例z′,也就是说,希望学习到与年龄无关的有关人物P的身份信息.为此,在构造训练样本时,每个人应包含尽可能多的年龄实例,使模型对于年龄的变化更健壮,并规定正样本为同一人不同年龄的图像组成的图像对,负样本为不同人的图像组成的图像对.给定训练集Z={(zi, yi)}i=1N,其中yi为类标签,也就是人物身份标识 (ID,identification),N为总人数,则图像对集合可表示为Ω={Ωk=(zi, zj)},k为Ω中第k个图像对.当zi和zj为同一个人时,图像对Ωk的标签l(Ωk) 等于1;否则等于-1,即
| $ l\left( {{\mathit{\Omega }_k}} \right) = l\left( {{z_i},{z_j}} \right) = \left\{ \begin{array}{l} 1, 若 l\left( {{z_i}} \right) = l\left( {{z_j}} \right)\\ - 1, 其他 \end{array} \right. $ | (5) |
以Ω作为输入,可通过最大化l(Ωk)×f(Ωk),使同一人的f(Ωk) 尽可能大,而不同人的f(Ωk) 尽可能小.更进一步,把 (LA, LB, c)T记为W,忽略l(Ωk)×f(Ωk)>1的图像对 (这里的约束值为1,并不重要,其可为任意的正值t,只不过学到的矩阵乘以t即可),则目标函数就可用类似铰链的损失函数表示为
| $ \begin{array}{*{20}{c}} {H\left( \mathit{\boldsymbol{W}} \right) = \sum\limits_\mathit{\Omega } {\max } \left\{ {0,1 - l\left( {{\mathit{\Omega }_k}} \right) \times f\left( {{\mathit{\Omega }_k}} \right)} \right\},}\\ {k = 1,2, \cdots ,{N^2}} \end{array} $ | (6) |
损失函数也可写为
深度卷积神经网络一般由1个或多个卷积层和顶端的全连接层组成,同时也包括关联权重和池化层. LA、LB和c可看成是全连接层的权重,网络的参数采用梯度下降法和链式求导法进行更新.
包含人物年龄信息的公共数据集规模都不大,因此设计的网络不很深,共包括7层:第1层为卷积层,包括32个尺寸5×5×3的卷积核,卷积的步长为2个像素;第2层为最大值池化层;第3层也为卷积层,包括32个尺寸为5×5×32的卷积核,卷积的步长为1个像素;第4层仍然为最大值池化层;第5~7层包括2个400维的和1个801维的全连接层,如图 1所示.在每个卷积层后采用修正线性单元 (ReLU,rectified linear unit) 进行非线性处理.修正线性函数的处理方法为:如果卷积计算的值小于0,则让其等于0;大于0,则保持原来的值不变. ReLU的做法虽然简单,但却能得到很好的稀疏性.实际上,这样7层的网络可分成特征学习、共同空间映射和测度学习3部分.特征学习阶段通过堆叠2个卷积-池化层和1个全连接层学习到400维的特征,第2个全连接层起到了把特征映射到共同空间的作用,第3个801维的全连接层实现了测度的学习.通过3个阶段同步学习,同时学到矩阵LA、LB和向量c.
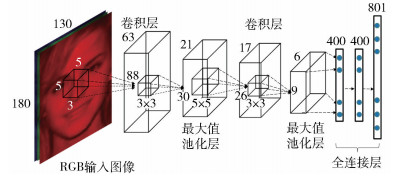
|
图 1 网络结构 |
存储有限的内存和大规模训练样本间的不匹配促使采用最小批选择策略.若有N个训练样本,样本对数目为O(N2),即使对于中等规模的数据集来说也不可能把所有的样本对都调入内存中.采用随机选择的方法选择样本对方法最简单,然而随机选择会使负样本数远远大于正样本数.例如,对于总人数为P,每人平均N张图像的带标签的数据集来说,负样本的数目为正样本的 (p-1)2倍,随机选择会使正负样本数严重不均衡.
为了解决上述问题,在每次迭代中随机选择固定数目的人,然后仅在这些人的图像中产生图像对.图像对保证穷举所有的正样本,负样本随机选择,但负样本数要和正样本数保持一定的比例,避免正负样本严重不平衡.
3.2.2 数据增强策略采用2种数据增强策略来增加训练样本数,减少过拟合现象.第1种策略为提取正样本对的图像块,使用这些图像块进行训练.图像块的高度和宽度与原图像成一定的比例,如输入图像大小为150×200,图像块占原图的90%,图像块的大小为135×180,这样正样本对的数目就扩大到原来的300倍.第2种策略是对正样本对的水平映射.理论上来说,正脸图像具有左右对称性,若分别对左右脸进行水平映射,原来的图像数就增加了2倍,相应地组合后的图像对数目为原来的9倍.但现实情况下有很多非正脸图像存在,随机选择1/4的正样本对进行水平映射,这样正样本对的数目就扩大到原来的3倍.经过这2种策略的数据增强,原来的正样本数扩大到原来的900倍,在一定程度上缓解了数据不足造成的过拟合问题.
3.2.3 部分神经元退出策略部分神经元退出策略是指在模型训练时随机让网络某些隐含层节点退出不起作用,退出的那些节点可以暂时认为不是网络结构的一部分,但它们的权重需要保留下来,因为下次样本输入时它可能又起作用.这样的策略可减少神经元间的相互适应,使模型更鲁棒,因为隐含节点都是以一定的概率随机出现,并不能保证相邻的节点每次都同时出现,因此使权值的更新不依赖于有固定关系隐含节点的共同作用.
对第1卷积层的输出按照0.5的比例置0,退出的神经元对于前馈网络没有贡献,也不参加反向传播.在模型测试阶段,使用均值网络来得到隐含层的输出,也就是在网络前向传播过程中的隐含层节点的输出值都要减半.
3.3 学习算法算法每次迭代首先选择最小批输入网络,然后构建图像对,再根据损失函数采用统计梯度下降法更新模型的参数.批处理形式下的损失函数可写为
| $ H\left( \mathit{\boldsymbol{W}} \right) = \sum\limits_{i,j \in m} {{{\left[ {1 - l\left( {{I_i},{I_j}} \right)f\left( {F\left( {{I_i}} \right),F\left( {{I_j}} \right)} \right)} \right]}_ + }} $ | (7) |
其中:〈Ii, Ij〉为图像对,F(Ii) 为图像Ii经过处理后的输出,{Ii}为被选的最小批中所有不同的图像集合,m为图像数.式 (7) 只与图像对有关,因此可简记为
| $ H\left( \mathit{\boldsymbol{W}} \right) = \sum\limits_{i,j \in m} {J\left( {F\left( {{I_i}} \right),F\left( {{I_j}} \right)} \right)} $ | (8) |
更新参数最直观的做法是根据损失函数先计算每个图像对的梯度,然后把所有图像对的梯度相加求和得到整体的梯度.图像对的损失可通过2幅图像的输出来定义,由于每个图像对包含的2幅图像会引起2次前向和反向传播,如果某个图像出现在多个图像对中,按图像对来计算损失函数时,该图像就会被重复计算多次.为了提高计算效率,可采用按最小批中不同的图像来计算损失,这样重复出现在多个图像对中的图像其前向和反向传播得以重复利用.为此式 (8) 可进一步写为
| $ H\left( \mathit{\boldsymbol{W}} \right) = H\left( {F\left( {{I_1}} \right),F\left( {{I_2}} \right), \cdots ,F\left( {{I_m}} \right)} \right) $ | (9) |
模型参数采用统计梯度下降法进行更新为
| $ \mathit{\boldsymbol{W = W}} - \alpha \frac{\partial }{{\partial \mathit{\boldsymbol{W}}}}H\left( \mathit{\boldsymbol{W}} \right) $ | (10) |
其中:α为学习率,
| $ \frac{{\partial H}}{{\partial {\mathit{\boldsymbol{W}}^{\left( l \right)}}}} = \sum\limits_{i = 1}^m {\frac{{\partial H}}{{\partial X_i^l}}\frac{{\partial X_i^l}}{{\partial {\mathit{\boldsymbol{W}}^{\left( l \right)}}}}} $ | (11) |
| $ \frac{{\partial H}}{{\partial X_i^l}} = \frac{{\partial H}}{{\partial X_i^{l + 1}}}\frac{{\partial X_i^{l + 1}}}{{\partial X_i^l}} $ | (12) |
算法1 深度联合学习算法
输入:
训练集X={(xi, li)}, 初始化W, α, t=0
输出:
网络参数W
1 while t < T do
2 t←t+1
3从X中随机选择参加训练的人脸图像
4从{〈Ii, Ij〉}中选择图像对训练集Ωk
5 for all {Ii} do
6 利用前向传播算法计算图像Ii的各层输出Xi(1), …, Xi(l), …, F(Ii)
7 end for
8 for all {Ii} do
9
10 for所有图像对Ωk, i.e.〈Ip, Iq〉 do
11 if f(Ωk)>1 then
12 if Ii=Ip then
13
14 else if Ii=Iq then
15
16 end if
17 end if
18 end for
19 根据式 (10) 和式 (11) 计算
20
21 end for
22 W(t)=W(t-1)-αtΔW
23 end while
4 实验实验采用了MORPH-Ⅱ数据库. MORPH-Ⅱ包含超过1.3万人的共5.5万多个人脸图像,年龄分布范围为16~77岁,平均每人4张图.选择数据库中1万个人,每人挑选年龄差距最大的2张图片,共计2万张图片做训练数据.从数据库中剩余的人中选择3 000个人,每个人年龄最大的图像做查询图像,年龄最小的图像组成检索数据库,也就是在检索数据库中每人仅有1张图片.为使实验结果具有可比性,实验设置与文献[3]相同.在该数据库上采用累积匹配特性 (CMC,cumulative match characteristic) 曲线评价算法性能. CMC曲线画出了前k(top-k) 个查询结果的累积匹配正确率.曲线由点{(i, ai) i=1, 2, …, k}组成,ai为前i个查询结果的累积正确率,即只要前i个查询结果中包含与查询图像是同一人的图像,则正确.实验首先验证不同训练策略对效果的影响,然后和目前较好的其他几种方法进行比较.
4.1 最小批选择对结果的影响图 2的CMC曲线展示了最小批中不同人数和图像对数组合对结果的影响,其中括号里的值分别代表人数和图像对数,为了比较的公平性,每种策略的正确率都是经过相同迭代次数获得的.每人在图像对中出现的次数都相同,例如 (60,4 800) 表示批中共有60个人,4 800个图像对,每人出现在80个图像对中.该组实验中的正负样本的比率固定为1:1.从图 2可以看出,(80,11 200) 的选择策略效果较优,但实际上,对top-10以上的性能,选择策略的影响相对已经比较小了.
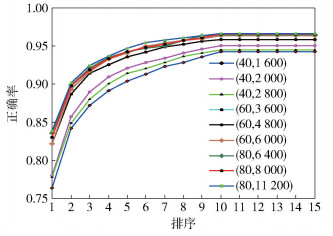
|
图 2 最小批中人数和图像对数对结果的影响 |
在MORPH-Ⅱ数据库上,JLA法也和其他跨年龄人脸识别方法做了比较,包括CARC法[3]、HFA法[2]、MFDA法[1]、Li等[5]提出的LPS+HFA方法和Park等[8]提出的方法.比较结果如表 1所示.
|
|
表 1 MORPH数据库上Rank-1的识别正确率 |
实验结果显示了JLA法的有效性,其性能接近目前已发表的最好方法LPS+HFA.对于top-10和top-20,JLA法的准确率分别为98.8%和99.34%,相应的CMC曲线图如图 3所示.实际上,top-10和top-20的准确率已经基本达到了实用的要求.与跨年龄人脸识别相关的诸多应用,如逃犯追捕系统,如果能成功推荐前10,甚至前20个相似的人脸图像,会大大降低工作的难度,并提高追捕的成功率.

|
图 3 JLA法在MORPH数据库上的CMC曲线 |
笔者提出的基于深度CNN的联合学习方法JLA在特征学习的同时可学习到最优的测度函数,避免了不合适的固定阈值带来的匹配错误,提高了匹配识别的正确率.此外,介绍了在模型学习过程中采用的多种新颖和有效的训练策略. JLA方法应用于跨年龄人脸识别的研究,在公开数据库MORPH-Ⅱ上的识别正确率达到了93.6%.
目前,实验所用的数据库还有很大的局限性,能满足人数众多、年龄跨度大2点要求的数据还比较少.因此,将致力于数据库的构建工作,收集、整理多年龄人脸图像,进一步增加可用数据.此外,将继续优化模型,使模型更加健壮,进一步提高其识别正确率.
| [1] | Li Zhifeng, Park U, Jain A K. A discriminative model for age invariant face recognition[J]. IEEE Transactions on Information Forensics and Security, 2011, 6(3): 1028–1037. doi: 10.1109/TIFS.2011.2156787 |
| [2] | Gong Dihong, Li Zhifeng, Lin Dahua, et al. Hidden factor analysis for age invariant face recognition[C]//ICCV 2013. Sydney:IEEE, 2013:2872-2879. |
| [3] | Chen Borchun, Chen Chusong, Hsu W H. Cross-age reference coding for age-invariant face recognition and retrieval[C]//ECCV 2014. Zurich:Springer, 2014:768-783. |
| [4] | Gong Dihong, Li Zhifeng, Tao Dacheng. A maximum entropy feature descriptor for age invariant face recognition[C]//CVPR 2015. Boston:IEEE, 2015:5289-5297. |
| [5] | Li Zhifeng, Gong Dihong, Li Xuelong, et al. Aging face recognition:a hierarchical learning model based on local patterns selection[J]. IEEE Transactions on Image Processing, 2016, 25(5): 2146–2154. doi: 10.1109/TIP.2016.2535284 |
| [6] | Xing E P, Jordan M I, Russell S, et al. Distance metric learning with application to clustering with side-information[C]//NIPS 2002. Vancouver:NIPS Foundation, 2002:521-528. |
| [7] | Li Zhen, Chang Shiyu, Liang Feng, et al. Learning locally adaptive decision functions for person verification[C]//CVPR 2013. Portland:IEEE, 2013:3610-3617. |
| [8] | Park U, Tong Yiying, Jain A K. Age-invariant face recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(5): 947–954. doi: 10.1109/TPAMI.2010.14 |


