在采用波束赋形和人工噪声的物理层安全传输系统中,利用人工噪声提高合法接收端的性能。发送端根据发送符号和信道系数判断人工噪声的分量是否对合法接收端的信号检测有益,并由此将人工噪声分为有益噪声和普通噪声,分别进行不同的波束赋形处理。在不改变人工噪声干扰窃听端接收的前提下,利用人工噪声提高合法接收端的接收性能。对采用相移键控(PSK)调制时的误码性能和保密容量进行理论分析和仿真,结果显示,与传统的人工噪声方案相比,所提出的人工噪声方案可提高合法接收端的性能,改善保密容量。
A strategy was studied which takes the advantage of artificial noise to improve the performance of legitimate user for physical layer security transmission systems using beamforming technology and artificial noise. Based on transmitted symbols and channel coefficients, the transmitter determines whether or not part of artificial noises are beneficial to the signal detection at the legitimate receiver. It divides the original artificial noises into two parts:constructive noises and common noises, then it designs beamforming vectors accordingly. By exploiting the constructive noises, the signal-to-noise ratio at the legitimate receiver is improved while that at the illegal receiver will remain the same. The bit error rate and the secrecy capacity are analyzed and simulated when phase shift keying modulation is used. It is demonstrated that the proposed scheme can improve the performance of the legal receiver and enhance secrecy capacity.
人工噪声[1](AN, artificial noise) 是一种有效的物理层安全技术,其基本思路是:发送端在发送信息的同时使用一部分功率来发送噪声,通过设计使噪声在劣化窃听端接收性能的同时不对合法接收端造成影响.在发送端完全未知窃听信道状态信息 (ECSI, eavesdropper’s channel state information) 的情况下,通常的设计方法则是使AN各向同性,均匀分布在合法信道的零空间[2-5].
现有的应用人工噪声的方案中,人工噪声不会对合法接收者的接收有任何帮助.实际上,在特定的情况下,人工噪声有可能对合法接收者而言是有益的.在发送端不知道ECSI的场景下,提出一种利用人工噪声的思路,对人工噪声进行波束赋形设计,使人工噪声在干扰窃听者的同时,也能提高合法接收者的性能,并针对相移键控 (PSK, phase shift keying) 调制方式,具体对人工噪声的设计、系统的误比特率和保密容量等性能进行分析.
1 人工噪声方案考虑包括一个源节点 (S, Source)、一个目的节点 (D, Destination) 和单个窃听节点 (E, Eavesdropper) 的无线网络模型,其中源节点具有N(>2) 根天线,目的节点和窃听节点均为单天线节点,S-D、S-E间的信道增益矢量分别用h、g表示,h=[h1, h2, …, hN]T,g=[g1, g2, …, gN]T.所有信道为相互独立的瑞利衰落信道,均为均值为0、方差为1的复高斯随机变量.
采用联合波束赋形和人工噪声的方案,对承载信息的信号和人工噪声使用不同的赋形矢量.标量x表示在一个传输时隙内要传输的M进制的PSK符号,具有单位功率,即E{|x|2}=1.为了符号的书写方便,省略时间下标.各发送天线发送的信号为
| $ {\mathit{\boldsymbol{x}}_1} = \sqrt {{P_s}} \mathit{\boldsymbol{w}}x + \sqrt {\frac{{{P_z}}}{{N - 1}}} \mathit{\boldsymbol{u}} $ | (1) |
其中:Ps是发送信号功率,w为信号的波束赋形矢量,w=[w1, w2, …, wN]T,Pz是人工噪声的总功率,u为经过波束赋形预处理后的噪声矢量,其设计随后介绍.
假设窃听节点是被动节点,发送端未知自己到窃听节点的信道状态,在此状况下,以最大化接收端的接收功率为目标,设计信息信号的波束赋形矢量w,易知
| $ \mathit{\boldsymbol{w}} = \frac{\mathit{\boldsymbol{h}}}{{\left\| \mathit{\boldsymbol{h}} \right\|}} $ | (2) |
目的节点和窃听节点接收到的信号分别为
| $ {y_{\rm{D}}} = {\mathit{\boldsymbol{h}}^H}{\mathit{\boldsymbol{x}}_{\rm{t}}} + {n_{\rm{D}}} = \sqrt {{P_{\rm{s}}}} {\mathit{\boldsymbol{h}}^{\rm{H}}}\mathit{\boldsymbol{w}}x + \sqrt {\frac{{{P_z}}}{{N - 1}}} {\mathit{\boldsymbol{h}}^{\rm{H}}}\mathit{\boldsymbol{u + }}{\mathit{\boldsymbol{n}}_{\rm{D}}} $ | (3) |
| $ {y_{\rm{E}}} = {\mathit{\boldsymbol{g}}^H}{\mathit{\boldsymbol{x}}_{\rm{t}}} + {n_{\rm{E}}} = \sqrt {{P_{\rm{s}}}} {\mathit{\boldsymbol{g}}^{\rm{H}}}\mathit{\boldsymbol{w}}x + \sqrt {\frac{{{P_z}}}{{N - 1}}} {\mathit{\boldsymbol{g}}^{\rm{H}}}\mathit{\boldsymbol{u + }}{\mathit{\boldsymbol{n}}_{\rm{E}}} $ | (4) |
其中nD~
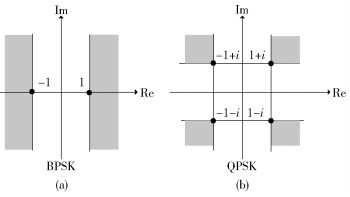
人工噪声有可能对接收端的信号检测和判决是有利的. 图 1所示为二进制相移键控 (BPSK,binary phase shift keying)、四相移键控 (QPSK, quadrature phase shift keying) 调制方式的星座图.当人工噪声使得接收信号向着阴影区域移动时,人工噪声有利于接收端作出正确的判决,此时的噪声即为有益噪声.为了能利用人工噪声,按照如下方法设计人工噪声波束赋形矩阵.
|
图 1 BPSK、QPSK星座图中有益噪声的区域 |
1) 随机生成N维人工噪声矢量z=[z1, z2, …, zN]T,zi~
2) 当arg (x)-π/M≤arg (vi)≤arg (x)+π/M时,则天线i发送的噪声对目的端有益,并计算vi在x上的投影值Re (vi) Re (x)+Imag (vi) Imag (x).
3) 找到第2) 步中计算所得的投影值中最大的一个,设对应下标为k,记z=vk=hk*zk,记z中去掉zk后的N-1维噪声矢量为z2,h中去掉hk后的N-1维信道增益矢量为h2,即z2=z\zk, h2=h\hk;若没有满足条件2) 的vi,表明不存在有利噪声,则令k=0,z=0,z2=z,h2=h.
4) 设计z的预加权值为w1=1,而z2的波束赋形矩阵W2指向h2的零空间,即满足h2HW2=0.
5) 波束赋形后的噪声u为
| $ \mathit{\boldsymbol{u = }}{w_1}z + {\mathit{\boldsymbol{W}}_2}{\mathit{\boldsymbol{z}}_2} $ | (5) |
将w和u表达式代入式 (3)(4) 中,接收端和窃听者接收到的信号可改写为
| $ {y_{\rm{D}}} = \sqrt {{P_{\rm{s}}}} \left\| \mathit{\boldsymbol{h}} \right\|x + \sqrt {\frac{{{P_z}}}{{N - 1}}} h_k^ * {z_k} + {n_{\rm{D}}} $ | (6) |
| $ {y_{\rm{E}}} = \sqrt {{P_{\rm{s}}}} \frac{{{\mathit{\boldsymbol{g}}^H}\mathit{\boldsymbol{h}}}}{{\left\| \mathit{\boldsymbol{h}} \right\|}}x + \sqrt {\frac{{{P_z}}}{{N - 1}}} g_k^ * {z_k} + \sqrt {\frac{{{P_z}}}{{N - 1}}} \mathit{\boldsymbol{g}}_2^{\rm{H}}{\mathit{\boldsymbol{W}}_2}{\mathit{\boldsymbol{z}}_2} + {n_{\rm{E}}} $ | (7) |
其中g2=g\gk,表示删除g中的元素gk.
在上述的人工噪声构造过程中,虽然根据h、随机产生的z,以及x控制了波束赋形,但由于z和h是随机的,发送有利人工噪声的天线的选择也是完全随机的,因此经波束赋形合成后的噪声u仍然具有很好的随机性,与发送信息并没有相关性,仍能很好地保护保密信息.
2 性能分析 2.1 误码率分析设发送端采用M-PSK调制,且各个符号等概分布.当接收端接收到人工噪声的相位在信号相位的±π/M范围内时,人工噪声有利于接收端作出正确的判决. h和z的相位都是在-π~+π间均匀分布,因此vi是有利的人工噪声的概率为1/M,N个人工噪声中存在有利噪声的概率为
| $ p\left( {k \ne 0} \right) = 1 - {\left( {1 - 1/M} \right)^N} $ | (8) |
随N增大,噪声有益的概率也将逐步增大.如对BPSK调制,在N>3时,噪声有益的概率超过0.9.
当k≠0时,对合法接收端,式 (6) 中第2项可以看作是信号部分 (对判断发送信号有利).平均接收功率为
| $ \begin{array}{*{20}{c}} {{{\bar P}_{{\rm{sD}}1}} = E\left( {{{\left| {\sqrt {{P_{\rm{s}}}} \left\| \mathit{\boldsymbol{h}} \right\|x + \sqrt {{P_z}/\left( {N - 1} \right)} h_k^ * {z_k}} \right|}^2}} \right) = }\\ {{P_{\rm{s}}}E\left( {{{\left\| \mathit{\boldsymbol{h}} \right\|}^2}} \right) + \frac{{{P_z}}}{{\left( {N - 1} \right)}}E\left( {{v_k}v_k^ * } \right) + }\\ {\sqrt {\frac{{{P_{\rm{s}}}{P_z}N}}{{\left( {N - 1} \right)}}} E\left( {\left\| \mathit{\boldsymbol{h}} \right\|{v_k}} \right) + \sqrt {\frac{{{P_{\rm{s}}}{P_z}N}}{{\left( {N - 1} \right)}}} E\left( {\left\| \mathit{\boldsymbol{h}} \right\|v_k^ * } \right) = }\\ {N{P_{\rm{s}}} + \frac{{f{P_z}}}{{\left( {N - 1} \right)}} + 2\sqrt {\frac{{f{P_{\rm{s}}}{P_z}N}}{{\left( {N - 1} \right)}}} } \end{array} $ | (9) |
其中f表示vk的功率放大倍数.根据第1节中噪声的构造方案,在选择有利的人工噪声时,当存在多个vi同时满足条件时,选取其中投影最大的一个作为vk,该方式与多天线的接收端,采取选择合并的方式进行信号分集接收的处理方式类似.根据文献[6],当接收端天线数目为J,采用选择合并方式后输出信号的功率增益为
| $ {\xi _J} = \sum\limits_{j = 1}^J {\frac{1}{j}} $ | (10) |
在本方案中,选取vk时,可能存在1~N个vi满足条件,即相当于选择合并的天线数目J可能取值为1~N,对应取值概率为pJ,因此vk的平均功率增益为
| $ \begin{array}{*{20}{c}} {f = \sum\limits_{J = 1}^N {{p_J}{\xi _J}} = }\\ {\sum\limits_{J = 1}^N {\left( {\frac{{\left( {\begin{array}{*{20}{c}} J\\ N \end{array}} \right){{\left( {\frac{1}{M}} \right)}^J}{{\left( {1 - \frac{1}{M}} \right)}^{N - J}}}}{\lambda }\sum\limits_{j = 1}^J {\frac{1}{j}} } \right)} }\\ {\lambda = \sum\limits_{J = 1}^N {\left( {\begin{array}{*{20}{c}} J\\ N \end{array}} \right){{\left( {\frac{1}{M}} \right)}^J}{{\left( {1 - \frac{1}{M}} \right)}^{N - J}}} } \end{array} $ | (11) |
接收端信道噪声功率Pn, D=σD2,接收端信噪比为
| $ {{\bar \gamma }_1} = {{\bar P}_{{\rm{s,D1}}}}/{{\bar P}_{{\rm{n,D}}}} = \frac{{N{P_{\rm{s}}}}}{{\sigma _{\rm{D}}^2}} + \frac{{f{P_z}}}{{\left( {N - 1} \right)\sigma _{\rm{D}}^2}} + \frac{2}{{\sigma _{\rm{D}}^2}}\sqrt {\frac{{f{P_{\rm{s}}}{P_z}N}}{{\left( {N - 1} \right)}}} $ | (12) |
当k=0时,式 (6) 中第2项为0,接收端的信号功率为
| $ {{\bar P}_{{\rm{s,D0}}}} = E\left( {{{\left| {\sqrt {{P_{\rm{s}}}} \left\| \mathit{\boldsymbol{h}} \right\|x} \right|}^2}} \right) = N{P_{\rm{s}}} $ | (13) |
噪声功率不变,Pn, D=σD2,接收端信噪比为
| $ {{\bar \gamma }_0} = {{\bar P}_{{\rm{s,D}}}}/{{\bar P}_{{\rm{n,D}}}} = \frac{{N{P_{\rm{s}}}}}{{\sigma _{\rm{D}}^2}} $ | (14) |
对M-PSK调制,每个符号含有lbM bit,因此接收端比特信噪比γb, m=γm/lbM,其中m取1或0,分别代表存在k≠0和k=0的两种情况.各天线发送信号根据合法信道系数进行了预加权,合法接收端的接收性能与采用多接收天线并采用最大比值合并方式的性能相当,根据文献[7],瑞利衰落信道下的平均误比特率为
| $ {{\bar p}_{\rm{e}}} = {\left( {\frac{{1 - \mu }}{2}} \right)^N}\sum\limits_{l = 0}^{N - 1} {\left( {\begin{array}{*{20}{c}} {N - 1 + l}\\ l \end{array}} \right){{\left( {\frac{{1 + \mu }}{2}} \right)}^l}} $ | (15) |
其中
| $ \begin{array}{*{20}{c}} {{{\bar p}_{{\rm{e,D}}}} = p\left( {k \ne 0} \right){{\bar p}_{{\rm{e,D\_1}}}} + p\left( {k = 0} \right){{\bar p}_{{\rm{e,D\_0}}}} = }\\ {\left( {1 - {{\left( {1 - \frac{1}{M}} \right)}^N}} \right){{\left( {\frac{{1 + {\mu _1}}}{2}} \right)}^N}\sum\limits_{l = 0}^{N - 1} {\left( {\begin{array}{*{20}{c}} {N - 1 + l}\\ l \end{array}} \right){{\left( {\frac{{1 + {\mu _1}}}{2}} \right)}^l}} + }\\ {{{\left( {1 - \frac{1}{M}} \right)}^N}{{\left( {\frac{{1 - {\mu _0}}}{2}} \right)}^N}\sum\limits_{l = 0}^{N - 1} {\left( {\begin{array}{*{20}{c}} {N - 1 + l}\\ l \end{array}} \right){{\left( {\frac{{1 + {\mu _0}}}{2}} \right)}^l}} } \end{array} $ | (16) |
其中
对窃听端而言,信号功率与k取值无关,考虑最坏的情况:窃听端不仅已知g,而且可以知道w,即窃听端可以进行正确的相位校正.校正后,窃听端进行检测的信号为
| $ \begin{array}{*{20}{c}} {{{\tilde y}_{\rm{E}}} = \sqrt {{P_{\rm{s}}}} \frac{{{{\left( {{\mathit{\boldsymbol{g}}^{\rm{H}}}\mathit{\boldsymbol{w}}} \right)}^ * }}}{{\left| {{\mathit{\boldsymbol{g}}^{\rm{H}}}\mathit{\boldsymbol{w}}} \right|}}\frac{{{\mathit{\boldsymbol{g}}^{\rm{H}}}\mathit{\boldsymbol{h}}}}{{\left\| \mathit{\boldsymbol{h}} \right\|}}x + \sqrt {\frac{{{P_z}}}{{N - 1}}} \frac{{{{\left( {{\mathit{\boldsymbol{g}}^{\rm{H}}}\mathit{\boldsymbol{w}}} \right)}^ * }}}{{\left| {{\mathit{\boldsymbol{g}}^{\rm{H}}}\mathit{\boldsymbol{w}}} \right|}}g_k^ * {z_k} + }\\ {\sqrt {\frac{{{P_z}}}{{N - 1}}} \frac{{{{\left( {{\mathit{\boldsymbol{g}}^{\rm{H}}}\mathit{\boldsymbol{w}}} \right)}^ * }}}{{\left| {{\mathit{\boldsymbol{g}}^{\rm{H}}}\mathit{\boldsymbol{w}}} \right|}}\mathit{\boldsymbol{g}}_2^{\rm{H}}{\mathit{\boldsymbol{W}}_2}{\mathit{\boldsymbol{z}}_2} + \frac{{{{\left( {{\mathit{\boldsymbol{g}}^{\rm{H}}}\mathit{\boldsymbol{w}}} \right)}^ * }}}{{\left| {{\mathit{\boldsymbol{g}}^{\rm{H}}}\mathit{\boldsymbol{w}}} \right|}}{n_{\rm{E}}}} \end{array} $ | (17) |
窃听端的信号平均接收功率为
| $ {{\bar P}_{{\rm{s,E}}}} = E\left( {{{\left| {\frac{{{{\left( {{\mathit{\boldsymbol{g}}^{\rm{H}}}\mathit{\boldsymbol{w}}} \right)}^ * }}}{{\left| {{\mathit{\boldsymbol{g}}^{\rm{H}}}\mathit{\boldsymbol{w}}} \right|}}\sqrt {{P_{\rm{s}}}} \frac{{{\mathit{\boldsymbol{g}}^{\rm{H}}}\mathit{\boldsymbol{h}}}}{{\left\| \mathit{\boldsymbol{h}} \right\|}}x} \right|}^2}} \right) = {P_{\rm{s}}} $ | (18) |
而噪声功率为人工噪声功率与信道噪声功率之和
| $ \begin{array}{*{20}{c}} {{{\bar P}_{{\rm{n,E}}}} = }\\ {E\left( {{{\left| {\frac{{{{\left( {{\mathit{\boldsymbol{g}}^{\rm{H}}}\mathit{\boldsymbol{w}}} \right)}^ * }}}{{\left| {{\mathit{\boldsymbol{g}}^{\rm{H}}}\mathit{\boldsymbol{w}}} \right|}}\left( {\sqrt {\frac{{{P_z}}}{{N - 1}}} g_k^ * {z_k} + \sqrt {\frac{{{P_z}}}{{N - 1}}} \mathit{\boldsymbol{g}}_2^{\rm{H}}{\mathit{\boldsymbol{W}}_2}{\mathit{\boldsymbol{z}}_2} + {n_{\rm{E}}}} \right)} \right|}^2}} \right) = }\\ {{P_{\rm{z}}} + \sigma _{\rm{E}}^2} \end{array} $ | (19) |
窃听端信噪比为
| $ {{\bar \gamma }_{\rm{E}}} = {{\bar P}_{{\rm{s,E}}}}/{{\bar P}_{{\rm{n,E}}}} = \frac{{{P_{\rm{s}}}}}{{\sigma _{\rm{E}}^2 + {P_{\rm{z}}}}} $ | (20) |
对窃听者,根据式 (16),接收信号中信息信号x前的系数为多个复高斯变量乘积的和,已不是复高斯分布,误码率的分析非常复杂,很难得到平均误比特率的闭式解,将在第3节通过仿真的方式进行分析.
2.2 保密容量分析把调制器、解调器和信道一起看作为一个M输入、M输出离散对称信道,合法信道和窃听信道的瞬时转移矩阵具有对称性,因此是M元离散对称信道,可以根据误码率得到瞬时信道容量,继而得到遍历保密容量.当信道转移矩阵中某一行概率为p1, p2, …, pM时,瞬时信道容量为
| $ {C_{u\_M}} = {\rm{lb}}M - H\left( {{p_1},{p_2}, \cdots ,{p_M}} \right) $ | (21) |
下标u取D或E,对应合法信道或窃听信道,下标M表示调制阶数,H(p1, p2, …, pM) 表示概率分布为p1, p2, …, pM的离散变量的熵,即
| $ H\left( {{p_1},{p_2}, \cdots ,{p_M}} \right) = - \sum\limits_{i = 1}^M {{p_i}{\rm{lb}}{p_i}} $ | (22) |
如采用格雷映射QPSK调制时,信道的瞬时转移矩阵为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}_{u\_q}} = }\\ {\left[ {\begin{array}{*{20}{c}} {{{\left( {1 - {p_{{\rm{u\_q}}}}} \right)}^2}} & {{p_{{\rm{u\_q}}}}\left( {1 - {p_{{\rm{u\_q}}}}} \right)} & {{p_{{\rm{u\_q}}}}\left( {1 - {p_{{\rm{u\_q}}}}} \right)} & {p_{{\rm{u\_q}}}^2}\\ {{p_{{\rm{u\_q}}}}\left( {1 - {p_{{\rm{u\_q}}}}} \right)} & {{{\left( {1 - {p_{{\rm{u\_q}}}}} \right)}^2}} & {p_{{\rm{u\_q}}}^2} & {{p_{{\rm{u\_q}}}}\left( {1 - {p_{{\rm{u\_q}}}}} \right)}\\ {{p_{{\rm{u\_q}}}}\left( {1 - {p_{{\rm{u\_q}}}}} \right)} & {p_{{\rm{u\_q}}}^2} & {{{\left( {1 - {p_{{\rm{u\_q}}}}} \right)}^2}} & {{p_{{\rm{u\_q}}}}\left( {1 - {p_{{\rm{u\_q}}}}} \right)}\\ {p_{{\rm{u\_q}}}^2} & {{p_{{\rm{u\_q}}}}\left( {1 - {p_{{\rm{u\_q}}}}} \right)} & {{p_{{\rm{u\_q}}}}\left( {1 - {p_{{\rm{u\_q}}}}} \right)} & {{{\left( {1 - {p_{{\rm{u\_q}}}}} \right)}^2}} \end{array}} \right]} \end{array} $ | (23) |
其中:下标u取D或E,对应合法信道或窃听信道,下标q表示QPSK调制方式,pu_q=Q(
| $ {C_{u\_q}} = {\rm{lb4}} - H\left( {\begin{array}{*{20}{c}} {\left( {1 - {p_{{\rm{u\_q}}}}} \right),{p_{{\rm{u\_q}}}}\left( {1 - {p_{{\rm{u\_q}}}}} \right),}\\ {{p_{{\rm{u\_q}}}}\left( {1 - {p_{{\rm{u\_q}}}}} \right),p_{{\rm{u\_q}}}^2} \end{array}} \right) $ | (24) |
Q(g) 函数定义
| $ Q\left( g \right) = \frac{1}{{\sqrt {2\pi } }}\int_g^\infty {{{\rm{e}}^{ - \frac{{{t^2}}}{2}}}{\rm{d}}t} $ | (25) |
遍历保密容量为
| $ {C_{{\rm{s}}\_q}} = E\left( {{{\left( {{C_{\rm{D}}} - {C_{\rm{E}}}} \right)}^ + }} \right) $ | (26) |
其中:CD和CE表示合法信道与窃听信道的瞬时保密容量,[x]+=max (x, 0),即当瞬时窃听信道信道容量大于合法信道信道容量时,瞬时保密容量为零.
对其他相位调制方式,分析过程与QPSK类似,这里不再赘述.
3 仿真结果在仿真中,合法信道和窃听信道是独立同分布的平坦瑞利衰落信道,信道增益服从均值为0、方差为1的独立复高斯分布;目的节点和窃听节点的噪声功率均为σD2=σE2=0 dBm,功率分配因子a定义为源端的发送信号功率Ps与总功率P的比值,即Ps=aP,Pz=(1-a)P.图例中合法信道表示为“LC”,窃听信道记为“EC”.仿真中将提出的方案与传统人工噪声方案进行了对比.在未知ESCI时,传统人工噪声方案[1]是:随机生成N维服从均值为0、协方差为σz2I的复高斯分布的人工噪声矢量z,并设计z的波束赋形矩阵W使其位于合法信道h的零空间,满足hHW=0, WHW=(N-1),不对合法接收者造成干扰.噪声的方差满足功率限制,即σz2=Pz/(N-1).而在合法接收端,人工噪声的接收功率为0.
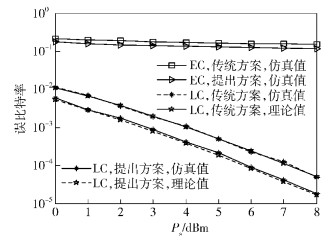
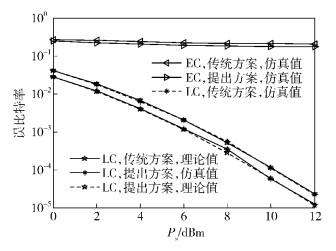
图 2和图 3分别是采用BPSK、QPSK调制方式时平均误比特率在发送功率变化时的仿真结果,a=0.5,天线数目N=4,合法接收端和窃听端均采用最大似然译码,且假设窃听端知道信号波束赋形矢量w.从仿真结果曲线可以看出,合法接收者误比特率的仿真结果与理论分析结果一致.与传统人工噪声方案比较,提出的方案在保证窃听信道误比特率基本不变的条件下,降低了主信道误比特率,对比图 3和图 2可知,相同条件下,BPSK误比特率改善效果优于QPSK,这是因为调制阶数M越小,人工噪声对判决有益的概率越大,接收端接收到的信号平均功率也更大,因此误比特率改善更显著.注意到在窃听者误比特率的仿真中,考虑了最坏的情况,即窃听端不仅已知窃听信道的信道增益g,而且可以知道发送端的信号波束赋形矢量w,其据此对接收信号进行正确的相位校正.实际上,窃听者很难获得w,此时其误比特率在整个仿真的信噪比范围内都约为0.5.
|
图 2 误比特率随Ps的变化 (BPSK) |
|
图 3 误比特率随Ps的变化 (QPSK调制) |
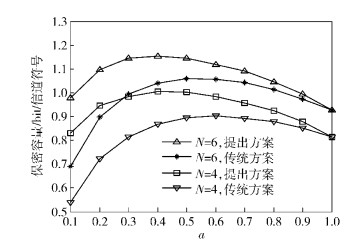
图 4是采用QPSK调制、功率分配因子a变化时保密容量的仿真结果,发送总功率P=0 dBm.保密容量由4万次独立的蒙特卡洛仿真结果取平均得到,下同.由仿真结果显示,随着功率分配因子a增大,保密容量先增大后减小,并且与传统方案的差异越来越小.该结果表明,信号和人工噪声功率的分配影响可获得的保密容量,存在一个最佳的功率分配方案使保密容量最大.当功率分配因子a较小时,发送人工噪声的功率较多,提出的方案利用有利的人工噪声使合法接收者的性能改善较大,因此相比较传统方案保密容量有较大的增加.而随着a的增大,人工噪声Pz逐渐减小,提出的方案对合法接收端信噪比的改善作用也逐渐减小,因此对保密容量的提升也相应减小.另外,增加发送天线数N,增加了分集阶数,分集增益增大,合法接收者的接收信噪比提高,故两种方案的保密容量均增加.
|
图 4 保密容量Cs与a、N的关系 (QPSK调制) |
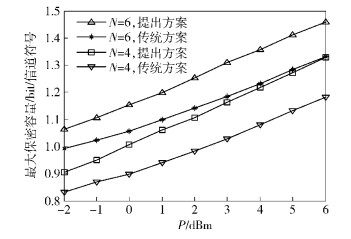
图 5是采用QPSK调制方式时,在最优的功率分配因子下 (最优功率分配因子由搜索方式得到,搜索步长为0.01),保密容量随发送总功率P变化的仿真结果.从图中可以看出,当采用最优的功率分配因子时,保密容量随发送端功率的增大而增大,提出的方案的性能始终优于传统方案.
|
图 5 最大保密容量与N、P的关系 (QPSK调制) |
对未知ECSI场景下,采用人工噪声的物理层安全传输方案中优化人工噪声使用的策略进行了研究,并针对PSK调制方式进行了理论分析和仿真.在发送端,通过分析合法信道的状态和人工噪声的具体取值,设计合适的噪声波束赋形,使其中一个天线发射的人工噪声可到达合法接收者,而该噪声有利于合法接收对保密信号做出正确的判决.其他天线发射的噪声则位于合法信道的零空间中,不对合法接收者产生干扰.对于窃听者而言,人工噪声仍然保持随机性,干扰其接收保密信号.针对PSK调制方式,给出了人工噪声及其波束赋形的设计方案,分析和仿真了误码性能和保密容量.分析和仿真结果表明,通过优化使用人工噪声的策略,可改善合法接收者的接收性能,而窃听者的接收性能则无明显变化,使安全性能得到提高.
| [1] | Negi R, Goel S. Secret communication using artificial noise[C]//IEEE Vehicular Technology Conference (VTC-2005-Fall). Dallas:IEEE, 2005:1906-1910. |
| [2] | Yang Yunchuan, Sun Cong, Zhao Hui, et al. Algorithms for secrecy guarantee with null space beamforming in two-way relay networks[J]. IEEE Transactions on Signal Process, 2014, 62(8): 2111–2126. doi: 10.1109/TSP.2014.2303942 |
| [3] | Zhu Fengchao, Gao Feifei, Zhang Tao, et al. Physical-layer security for full-duplex communications with self-interference mitigation[J]. IEEE Transactions on Wireless Communications, 2016, 15(1): 329–340. doi: 10.1109/TWC.2015.2472527 |
| [4] | Zhang Xi, Zhou X Y, Mckay M R, et al. Artificial-noise-aided secure multi-antenna transmission with limited feedback[J]. IEEE Transactions on Wireless Communications, 2015, 14(5): 2742–2754. doi: 10.1109/TWC.2015.2391261 |
| [5] | Zhang Liyun, Zhang Haixia, Wu Dalei, et al. Improving physical layer security for MISO systems via using artificial noise[C]//2015 IEEE Global Communications Conference (GLOBECOM). San Diego, CA:IEEE, 2015:1-6. |
| [6] | Schwartz M, Bennett W R, Stein S. Communication systems and techniques[M]. New York: McGraw-Hill, 1966: 432-439. |
| [7] | Simon M K, Alouiion M S. Digital communication over fading channels[M]. New York: John Wiley & Sons, 2000: 265-267. |


