通过研究功率分配对空间耦合数据传输的性能影响,在空间耦合数据流间干扰完全消除的情况下,利用密度进化与势能函数证明了等功率传输性能最优。为了以较少的性能损失为代价,减少等功率传输引起的高检测复杂度,提出了一种功率分配算法实现非等功率传输。外信息转换图分析和仿真结果证实了理论分析的正确性和所提算法的可行性。
In order to investigate the performance of power allocation for spatially coupling data transmission, under conditions in which the interference of among coupling data streams is eliminated completely, the author proved that the system performance can achieve optimal for equal power transmission by utilizing density evolution and potential function. To reduce higher detection complexity caused by equal power transmission at the price of a small performance loss, a new power allocation algorithm was proposed to implement unequal power transmission. Extrinsic information transfer chart analyses and simulation results verify the correctness of theory analysis and the feasibility of the proposed algorithm.
随着未来移动通信和物联网的快速发展,这对系统容量和频谱效率提出了更高的要求.非正交多址接入 (NOMA, non-orthogonal multiple access) 技术作为5G的一项关键技术, 与当前4G所采用的正交多址接入技术相比,NOMA显著提升了系统的频谱效率[1].
空间耦合传输作为一种NOMA技术能够避免传统CDMA系统遇到的干扰受限问题,它已从理论上被证明当信噪比趋向无穷大时,支持的系统负载也趋向无穷大[2],其背后原理是利用了空间耦合码的门限饱和效应[3].随后, Truhachev等[4]表明空间耦合传输系统可达到加性白色噪声信道上的容量.
空间耦合传输的在接收端,Schlegel等[2, 4]采用迭代干扰消除的方法进行检测,但采用该算法的前提需要叠加的用户数足够大满足高斯近似,而叠加用户数的增加又加大了检测复杂度.在大规模稀疏扩频CDMA系统中,置信传播 (BP, belief propagation) 是接近性能最优的检测算法[5-6].空间耦合数据传输系统具有稀疏扩频CDMA特性.因此,在接收端笔者采用BP算法检测信号.当叠加的用户数或数据流太多时,BP检测复杂度也会增加,但可采用用户调度方式解决.如用户间两两配对分多个组,然后每组内的用户再采用笔者所提的空间耦合方式实现数据传输.
在多址接入系统中,功率分配是影响系统性能和复杂度的关键因素.如在交织多址接入系统中,在一定条件下等功率可达系统性能最优[7],但是等功率不能有效克服用户间干扰,增加了迭代检测次数.而非等功率却能促进迭代收敛,从而降低检测复杂度[8].笔者研究了功率分配对空间耦合多址接入系统性能影响.通过高斯计算得到了空间耦合系统的密度进化方程式,然后利用该方程式和势能函数对系统性能进行分析,最后通过外信息转换 (EXIT, extrinsic information transfer) 图分析评估和模拟仿真验证.
1 系统模型及检测算法 1.1 系统模型描述假设用户1和用户2共有L层数据流同时传输,采用二进制相移键控调制后,再乘以对应的幅值
| $ {\mathit{\boldsymbol{y}}_t} = \sum\limits_{l \in \psi } {\sum\limits_{m \in \varphi } {\eta {\mathit{\boldsymbol{s}}_{t,m,l}}{b_{m,l}} + {\mathit{\boldsymbol{z}}_t}} } $ | (1) |
|
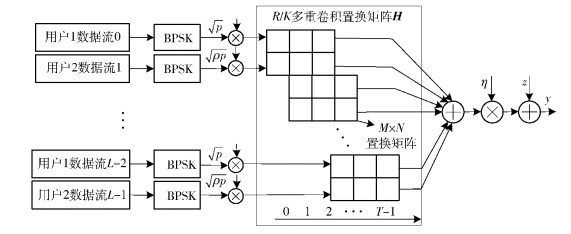
图 1 两用户空间耦合数据传输发送框图 |
其中m∈ϕ={0, …, M-1}, l∈ψ={0, …, L-1},t∈ω={0, …, T-1}.式 (1) 中zt~N(0, σz2IN) 表示噪声的均值为0,方差为σz2的高斯分布,则系统信噪比为γ=1/σz2. bm, l∈{-1, +1}表示数据流l的第m个符号, st, m, l=(s0, t, m, l, …, sN-1, t, m, l)T表示在t时间内数据流l的第m个符号扩频序列,其中,sn, t, m, l,n∈ϑ={0, …, N-1}表示扩频序列的第n个符号.若定义St, l=(st, 0, l, …, st, M-1, l),则矩阵H可表示为
| $ \mathit{\boldsymbol{H = }}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{S}}_{0,0}}} & \cdots & {{\mathit{\boldsymbol{S}}_{0,R - 1}}} & {} & {} & {} & {}\\ \vdots & \ddots & {} & \ddots & {} & {} & {}\\ {{\mathit{\boldsymbol{S}}_{R - 1,0}}} & \cdots & {{\mathit{\boldsymbol{S}}_{R - 1,\beta - 1}}} & {} & \ddots & {} & {}\\ {} & {} & {} & \ddots & {} & \ddots & {}\\ {} & {} & {} & {} & {{\mathit{\boldsymbol{S}}_{T - 1,L - \beta }}} & \cdots & {{\mathit{\boldsymbol{S}}_{T - 1,L - 1}}} \end{array}} \right] $ |
空白处对应的值均为0.
1.2 BP检测笔者研究的耦合系统可用稀疏二分图表示[4-5],变量节点和信道节点分别表示传输符号和在某时刻的接收信号.令ə(n, t) 和φ(m, l) 分别表示与信道节点sn, t相连的变量节点集合,与变量节点vm, l相连的信道节点集合, ə(n, t)\(m, l) 表示与信道节点sn, t相连除vm, l之外的变量节点集合, φ(m, l)\(n, t) 表示与变量节点vm, l相连除sn, t之外信道节点集合.再令B[n, t]和H[n, t]分别表示在时间t内第n时刻传输的符号向量和对应的扩频符号向量,
1) 初始化各变量节点软信息
| $ L_{{v_{m,l}} \to {s_{n,t}}}^{\left( 0 \right)} = 0,\forall m \in \phi ,\forall l \in \psi ,\forall n \in \vartheta ,\forall t \in \omega $ | (2) |
2) 更新信道节点的软信息
| $ \begin{array}{*{20}{c}} {L_{{s_{n,t}} \to {v_{m,l}}}^{\left( i \right)} = }\\ {\ln \frac{{\sum\limits_{\begin{array}{*{20}{c}} {\left\{ {{b_{\tilde m,\tilde l}}} \right\}}\\ {{b_{m,l}} = 1} \end{array}} {\exp \left( {\sum\limits_{\begin{array}{*{20}{c}} {\left( {\tilde m,\tilde l} \right) \in }\\ {\partial \left( {n,t} \right)\backslash \left( {m,l} \right)} \end{array}} {\frac{{{b_{\tilde m,\tilde l}}L_{{v_{\tilde m,\tilde l}} \to {s_{n,t}}}^{\left( {i - 1} \right)}}}{2} - \frac{{{{\left\| {{y_{n,t}} - \eta \mathit{\boldsymbol{H}}_{\left[ {n,t} \right]}^{\rm{T}}{\mathit{\boldsymbol{B}}_{\left[ {n,t} \right]}}} \right\|}^2}}}{{2\sigma _z^2}}} } \right)} }}{{\sum\limits_{\begin{array}{*{20}{c}} {\left\{ {{b_{\tilde m,\tilde l}}} \right\}}\\ {{b_{m,l}} = - 1} \end{array}} {\exp \left( {\sum\limits_{\begin{array}{*{20}{c}} {\left( {\tilde m,\tilde l} \right) \in }\\ {\partial \left( {n,t} \right)\backslash \left( {m,l} \right)} \end{array}} {\frac{{{b_{\tilde m,\tilde l}}L_{{v_{\tilde m,\tilde l}} \to {s_{n,t}}}^{\left( {i - 1} \right)}}}{2} - \frac{{{{\left\| {{y_{n,t}} - \eta \mathit{\boldsymbol{H}}_{\left[ {n,t} \right]}^{\rm{T}}{\mathit{\boldsymbol{B}}_{\left[ {n,t} \right]}}} \right\|}^2}}}{{2\sigma _z^2}}} } \right)} }}} \end{array} $ | (3) |
3) 更新变量节点软信息
| $ L_{{v_{m,l}} \to {s_{n,t}}}^{\left( i \right)} = \sum\limits_{\left( {\tilde n,\tilde t} \right) \in \varphi \left( {m,l} \right)\backslash \left( {n,t} \right)} {L_{{s_{\tilde n,\tilde t}} \to {v_{m,l}}}^{\left( i \right)}} $ | (4) |
4) 判决
经过I次迭代后做硬判决,即
| $ {{\hat v}_{m,l}} = \mathop {\arg max}\limits_{{v_{m,l}}} L_{{v_{m,l}}}^{\left( I \right)} $ |
根据Takeuchi等[5-6]所提的方法,笔者经过公式推导得到不同功率下的空间耦合系统的信干噪比与干扰噪声功率的耦合递归表达式,可表示为
| $ r_l^{\left( i \right)} = \frac{2}{{K\left( {1 + \rho } \right)}}\sum\limits_{r = 0}^{R - 1} {\frac{{{\rho ^\delta }}}{{\sigma _{\left( {r + \left\lfloor {l/\beta } \right\rfloor } \right)}^2\left( i \right)}}} $ | (5) |
| $ \sigma _t^2\left( i \right) = \sum\limits_{k = 0}^{{K_t} - 1} {\frac{{{\rho ^\delta }}}{{R\left( {1 + \rho } \right)}}\zeta \left( {r_\lambda ^{\left( {i - 1} \right)}} \right)} + \sigma _z^2 $ | (6) |
其中λ=k+(t-R+1)β, 在式 (5)(6) 中,若l和λ是偶数,δ=0;若l和λ是奇数, δ=1,并且∀l∈ψ,rl(0)=0.当t≤1时,(t-R+1)β=0.其中rl(i)表示第i次迭代的第l层数据流的信干噪比,σt2(i) 表示第i次迭代后时间t内的干扰噪声功率,ζ(a) 表示信干噪比a的最小均方差函数[4],其公式ζ(a)=
| $ \begin{array}{*{20}{c}} {\sigma _t^2\left( i \right) = }\\ {\sum\limits_{k = 0}^{{K_t}/\beta - 1} {\frac{{{\rho ^\delta }}}{{R\left( {1 + \rho } \right)}}\zeta \left( {\frac{2}{{K\left( {1 + \rho } \right)}}\sum\limits_{r = 0}^{R - 1} {\frac{1}{{\sigma _{\left( {r + \left\lfloor {\lambda /\beta } \right\rfloor } \right)}^2\left( {i - 1} \right)}}} } \right)} + }\\ {\sum\limits_{k = 0}^{{K_t}/\beta - 1} {\frac{\rho }{{R\left( {1 + \rho } \right)}}\zeta \left( {\frac{{2\rho }}{{K\left( {1 + \rho } \right)}}\sum\limits_{r = 0}^{R - 1} {\frac{1}{{\sigma _{\left( {r + \left\lfloor {\lambda /\beta } \right\rfloor } \right)}^2\left( {i - 1} \right)}}} } \right)} + \sigma _z^2} \end{array} $ | (7) |
与笔者所提的空间耦合系统相对应的传统系统称之为非耦合系统,它是指各时刻叠加的数据流相同即Kt=K,且对应的干扰噪声功率也相同.当i→∞时,则有σ(r+
| $ x = \frac{1}{{\left( {1 + \rho } \right)}}\zeta \left( {\frac{2}{{\beta x\left( {1 + \rho } \right)}}} \right) + \frac{\rho }{{\left( {1 + \rho } \right)}}\zeta \left( {\frac{2}{{\beta x\left( {1 + \rho } \right)}}} \right) + \sigma _z^2 $ | (8) |
式 (8) 最多有3个解[4],定义为x(1) < x(2) < x(3).
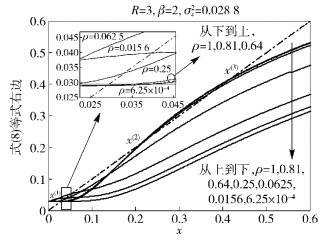
为了直观显示这3个解并便于理解和分析,给出了β=2, σz2=0.028 8,ρ取不同值时式 (8) 曲线,如图 2所示,图中的实线与虚线相交点对应着式 (8) 的解. 图 2中的各条实线使用了文献[10]所给精度1%的近似函数代替ζ(a), 其中σz2=0.028 8是根据耦合递归式 (5)(6) 在L足够大,R=3,β=2,ρ=1,i→∞时计算得到.取该噪声功率的值能保证在β=2时,式 (7) 收敛于最小解x(1)=σz2,使空间耦合数据流之间的干扰完全消除.
|
图 2 不同功率分配下的式 (8) 函数曲线 |
空间耦合系统收敛性能可使用势能函数方法进行分析[4, 11].令U(x, β, ρ) 表示空间耦合系统的势能函数.若R足够大,
| $ \begin{array}{*{20}{c}} {U\left( {x,\beta ,\rho } \right) = \ln \left( {\frac{{x + {{\tilde x}^{\left( 1 \right)}}}}{{{{\tilde x}^{\left( 1 \right)}}}}} \right) - \frac{{\sigma _z^2x}}{{{{\tilde x}^{\left( 1 \right)}}\left( {x + {{\tilde x}^{\left( 1 \right)}}} \right)}} - }\\ {\frac{\beta }{2}\left( {\int_{\frac{2}{{\beta \left( {1 + \rho } \right)\left( {x + {{\tilde x}^{\left( 1 \right)}}} \right)}}}^{\frac{2}{{\beta \left( {1 + \rho } \right){{\tilde x}^{\left( 1 \right)}}}}} {\zeta \left( y \right){\rm{d}}y} + \int_{\frac{{2\rho }}{{\beta \left( {1 + \rho } \right)\left( {x + {{\tilde x}^{\left( 1 \right)}}} \right)}}}^{\frac{{2\rho }}{{\beta \left( {1 + \rho } \right){{\tilde x}^{\left( 1 \right)}}}}} {\zeta \left( y \right){\rm{d}}y} } \right)} \end{array} $ | (9) |
其中
由式 (9) 可知,当γ,β一定时,又因
命题1 假设γ,β一定,R足够大,若
证明 见附录.
由此命题可知,ρ=1时即等功率的耦合传输系统性能最优,但是等功率不能有效克服数据流的干扰,需要更多的迭代次数才能收敛[7],增加了检测复杂度增加.而非等功率即ρ < 1却能有效克服数据流间的干扰,减少迭代检测次数降低复杂度[8],因此需要折中考虑性能与复杂度.
3 功率分配算法折中考虑性能与复杂度,达到以较少的性能损失使复杂度降低目的,笔者给出了一种计算功率分配因子ρ的算法,通过命题1的证明可知需分以下两种情况说明.
情况1 若
步骤1 计算ρ*.由命题1的证明中可知,在情况1中,存在
| $ {\rho ^ * } = \inf \left\{ {\rho :\mathop {\min }\limits_{x \in \left[ {0,1} \right],\rho \in \left( {0,1} \right)} U\left( {x,\beta ,\rho } \right) \ge 0} \right\} $ | (10) |
对任意ρ≥ρ*,式 (7) 都能收敛于x(1).由命题证明可知当ρ*→0,也会使min x∈[0,1]U (x, β, ρ*)=0.由第4节的EXIT分析可知,ρ*→0将使系统性能很差, 难以收敛,因此应从1到0递减查找ρ*,使
步骤2 计算目标功率因子ρtar.把ρ=1代入式 (8) 右边得ζ(1/(βx))+σz2.因式 (8) 不是线性函数, 难以直接计算
| $ {{\tilde x}^{\left( 1 \right)}} = \arg \mathop {\min }\limits_{x \in \left[ {0,1} \right]} \left\{ {\left| {\zeta \left( {1/\left( {\beta x} \right)} \right) + \sigma _z^2 - x} \right|} \right\} $ | (11) |
由命题1的证明中可知,x(1)(ρ)>
| $ \begin{array}{*{20}{c}} {{\rho _{{\rm{tar}}}} = \arg \mathop {\min }\limits_{\rho \in \left[ {{\rho ^ * },1} \right)} \left\{ {\left| {\frac{1}{{\left( {1 + \rho } \right)}}\zeta \left( {\frac{2}{{\beta x_{{\rm{tar}}}^{\left( 1 \right)}\left( {1 + \rho } \right)}}} \right)} \right. + } \right.}\\ {\left. {\left. {\frac{\rho }{{\left( {1 + \rho } \right)}}\zeta \left( {\frac{2}{{\beta x_{{\rm{tar}}}^{\left( 1 \right)}\left( {1 + \rho } \right)}}} \right)\sigma _z^2 - x_{{\rm{tar}}}^{\left( 1 \right)}} \right|} \right\}} \end{array} $ | (12) |
为了验证该算法的有效性,将在第4节通过EXIT分析验证.
情况2 若
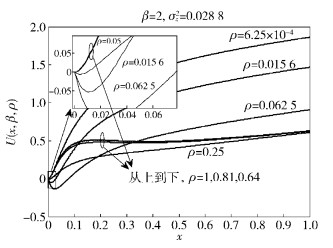
针对情况2,可直接通过势能函数曲线验证其结论.如图 3所示,当ρ=6.25×10-4, 0.64, 0.81, 1时,因在图 3中难以观察,其对应的最小值分别为-5.33×10-4,-1.15×10-5,-2.06×10-6,1.49×10-7.可见当ρ=1时,其势能函数的最小值几乎等于0;否则,
|
图 3 不同功率分配下的势能函数曲线 |
EXIT图是分析各译码器之间软输入软输出信息转换的有效工具,能够可视化观察到BP检测算法处理过程.本节通过EXIT分析命题1的正确性和所提方法的可行性,评估耦合系统的性能及复杂度.令IA, VND(IA, CND) 是变量节点 (信道节点) 和先验LLR的平均互信息,IE, VND(IE, CND) 是变量节点 (信道节点) 和外部LLR的平均互信息.
变量节点EXIT函数可由如下公式得到[12]:
| $ {I_{{\rm{E,VND}}}}\left( {R,{I_{{\rm{A,VND}}}}} \right) = J\left( {\sqrt {\left( {R - 1} \right){{\left( {{J^{ - 1}}\left( {{I_{{\rm{A,VND}}}}} \right)} \right)}^2}} } \right) $ | (13) |
其中J为软信息对数似然比均方差的函数,该函数的定义参见文献[12-13].理想情况下,变量节点和信道节点外部互信息曲线的相交点位于误比特率 (BER, bit error ratio) 任意小处,即在到达相交点 (IA, IE)=(1, 1) 之前,两条曲线不相交,此时系统性能最优[13],这时两条曲线间将出现一条通道.若在到达 (1, 1) 点之前相交,则会产生比相交点在 (1, 1) 处更高的BER.因此,两条曲线的相交点越靠近 (1, 1),BER就越低系统性能越好.另外,两条曲线之间的通道越大,则需要更少的迭代次数收敛,复杂度越低.反之,复杂度增加[13].
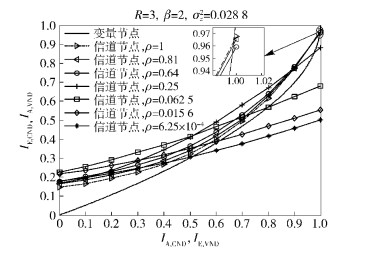
当ρ∈[ρ*, 1],β=2,R=3时,
|
图 4 不同功率分配下的EXIT |
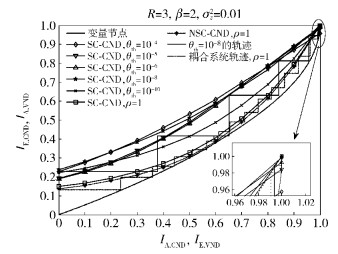
为了验证笔者所提的功率分配算法的有效性,图 5给出了不同误差门限θth和等功率传输下耦合及非耦合系统所对应的EXIT曲线图. 图 5中SC-CND和NSC-CND分别表示耦合系统和非耦合系统中的信道节点.当取θth=10-4, 10-5, 10-6, 10-8, 10-10时,利用笔者所提的功率分配算法得到对应的目标功率分别为ρtar=0.14, 0.21, 0.28, 0.46, 0.85.从该图可以看到θth=10-8所对应的EXIT曲线通道宽度要大于θth=10-10而接近或大于θth=10-4, 10-5, 10-6所对应的宽度,这表明θth=10-8需要更少的迭代次数就能收敛.再通过观察EXIT曲线的交点,θth=10-8的交点几乎与θth=10-10及ρ=1的交点重合,比θth=10-4, 10-5, 10-6的交点更靠近于 (1, 1) 处,这暗示θth=10-8的性能要优于θth=10-4, 10-5, 10-6且接近于ρ=1的系统性能. 图 5中还给出了θth=10-8及ρ=1时的耦合系统轨迹,θth=10-8时系统经过5次迭代后将收敛,而ρ=1需要19次迭代收敛,极大地减少了所需的迭代次数.作为比较,还给出了传统的非耦合系统等功率EXIT曲线,其EXIT曲线通道非常狭窄,表明其难以克服数据流间的干扰使系统收敛.
|
图 5 不同的误差门限值及等功率下的EXIT图 |
为了进一步验证所提算法的正确及有效性,笔者给出了不同功率分配下系统收敛所需要的平均迭代次数以及蒙特卡罗仿真评估系统的BER性能.设置系统两用户总数据流的个数为L=36,R/K MCP中的单位置换矩阵的维度为100,其中R=3,β=2.令最大迭代次数和帧的总数分别为30和200,在最大迭代次数内保证系统都能收敛正确检测,经统计,θth=10-4、10-5、10-6、10-8、10-10和ρ=1需要的平均迭代次数分别为5.96、6.13、6.15、5.07、7.99和18.55.可见,θth=10-8所需的迭代次数接近θth=10-4、10-5、10-6,且少于θth=10-10和远小于ρ=1所需的次数.

|
图 6 不同功率分配下的迭代次数与BER性能 |
图 6所示为系统的BER性能随迭代次数的变化.
在BER为10-3处,等功率耦合数据传输需要迭代20次,而θth=10-4、10-8则只需要大概4次迭代,节约了近5倍的迭代次数.随着迭代次数的增加,数据流之间的干扰不断减少,使得等功率及非等功率数据传输的BER性能逐渐降低.当达到一定迭代次数后,数据流间的干扰及噪声趋向于定值.因此BER性能将不再随迭代次数的增加而减小,如图 6中θth=10-4的曲线所示.对于θth=10-8和ρ=1的耦合数据传输系统,若迭代次数均较大,所有随机生成的数据均能正确检测.为了比较二者的BER性能,笔者设置帧总数为10 000,最大迭代次数分别为7次和26次, 保证二者均收敛.由图 6可见,二者的BER性能几乎相同,但后者所需的迭代次数将近是后者的4倍.从图 6可以看到,虽然迭代次数不断增加,等功率非耦合传输系统的BER性能仍然很差,其性能远不如等功率的耦合传输系统,这是因为等功率的非耦合系统.难以克服数据流间的干扰,而等功率的耦合系统利用耦合结构优点,也即是耦合系统的两端有较少的数据流叠加,因而其面临的干扰相对较少,能够获得更可靠的软信息.该可靠的软信息又能随着迭代次数的增加不断向中间传播[4-5],最终使中间处的数据流也能获得可靠的信息,从而使耦合系统的性能得到显著提升.
5 结束语笔者利用密度进化和势能函数证明了在数据流间干扰完全消除的情况下等功率耦合传输性能最优.提出了一种耦合数据传输的功率分配算法,以较少的性能损失极大地减少检测复杂度. EXIT图分析和模拟仿真结果表明, 与等功率传输相比,非等功率传输减少了近4倍的迭代次数,而BER性能损失可忽略.
附录当ρ→0和ρ→1,式 (8) 变为
| $ x = \zeta \left( {\frac{2}{{\beta x}}} \right) + \sigma _z^2 $ | (14) |
| $ x = \zeta \left( {\frac{1}{{\beta x}}} \right) + \sigma _z^2 $ | (15) |
因ζ(·) 是减函数,所以
| $ x = \zeta \left( {\frac{2}{{\beta x}}} \right) + \sigma _z^2 \le \zeta \left( {\frac{1}{{\beta x}}} \right) + \sigma _z^2 $ | (16) |
这表明ρ→0的干扰噪声功率值大于ρ→1的干扰噪声功率.
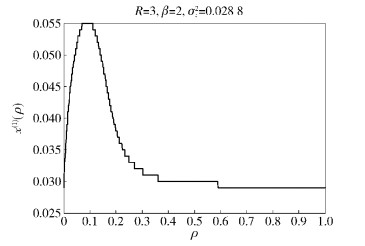
对每个ρ∈(0, 1]的取值,式 (8) 总有一个最小解x(1)与之相对应,因此笔者定义关于ρ的函数最小解函数为x(1)(ρ).由式 (14)(15) 可知,ρ∈(0, 1),x(1)(ρ)≥
|
图 7 x(1)(ρ) 函数曲线 |
因变量节点传递给信道节点的LLR是均值为2
当ρ∈[ρ*, 1),
根据式 (10) 计算得到ρ*=0.085.如图 2所示,当ρ∈[ρ*, 1) 时,x(1)(ρ)>x(1);当ρ→1或ρ→0时,x(1)(ρ)→
当ρ=1时,可分为
| [1] | Dai L, Wang B, Yuan Y, et al. Non-orthogonal multiple access for 5G:solutions, challenges, opportunities, and future research trends[J]. IEEE Communications Magazine, 2015, 53(9): 74–81. doi: 10.1109/MCOM.2015.7263349 |
| [2] | Schlegel C, Truhachev D. Multiple access demodulation in the lifted signal graph with spatial coupling[J]. IEEE Transactions on Information Theory, 2013, 59(4): 2459–2470. doi: 10.1109/TIT.2012.2232965 |
| [3] | Kudekar S, Richardson T, Urbanke R. Threshold saturation via spatial coupling:why convolutional LDPC ensembles perform so well over the BEC[J]. IEEE Transactions on Information Theory, 2011, 57(2): 803–834. doi: 10.1109/TIT.2010.2095072 |
| [4] | Truhachev D, Schlegel C. Coupling data transmission for capacity-achieving multiple-access communications[EB/OL]. (2012-01-12)[2016-01-02]. https://arxiv.org/abs/1209.5785. |
| [5] | Takeuchi K, Tanaka T, Kawabata T. Performance improvement of iterative multiuser detection for large sparsely spread CDMA systems by spatial coupling[J]. IEEE Transactions on Information Theory, 2015, 61(4): 1768–1794. doi: 10.1109/TIT.2015.2400445 |
| [6] | Guo D, Wang C. Multiuser detection of sparsely spread CDMA[J]. IEEE Journal on Selected Areas in Communications, 2008, 26(3): 421–431. doi: 10.1109/JSAC.2008.080402 |
| [7] | Lau M, Yue W, Ping L. Equal power allocation of IDMA systems:feasibility, optimality, and throughput[J]. IEEE Transactions on Wireless Communications, 2009, 8(2): 746–756. doi: 10.1109/TWC.2009.070744 |
| [8] | Liu L, Tong J, Ping L. Analysis and optimization of CDMA systems with chip-level interleavers[J]. IEEE Journal on Selected Areas in Communications, 2006, 24(1): 141–150. doi: 10.1109/JSAC.2005.858896 |
| [9] | Lentmaier M, Sridharan A, Zigangirov K, et al. Terminated LDPC convolutional codes with thresholds close to capacity[C]//2005 IEEE International Symposium on Information Theory (ISIT). Adelaide, Australia:[s.n.], 2005:1372-1376. |
| [10] | Burnashev M, Schlegel C, Krzymien W, et al. Analysis of the dynamics of iterative interference cancellation in iterative decoding[J]. Problems of Information Transmission, 2004, 40(4): 297–317. doi: 10.1007/s11122-005-0001-y |
| [11] | Yedla A, Jian Y Y, Nguyen P S, et al. A simple proof of threshold saturation for coupled scalar recursions[C]//2012 IEEE 7th International Symposium on Turbo Codes and Iterative Information Processing (ISTC). Gothenburg, Sweden:[s. n.], 2012:51-55. |
| [12] | Razavi R, Al-Imari M, Imran M A, et al. On receiver design for uplink low density signature OFDM (LDS-OFDM)[J]. IEEE Transactions on Communications, 2012, 60(11): 3499–3508. |
| [13] | Ten Brink S. Convergence behavior of iteratively decoded parallel concatenated codes[J]. IEEE Transactions on Communications, 2001, 49(10): 1727–1737. doi: 10.1109/26.957394 |



