提出了一种新的移动相机下的地面运动目标分割方法,运用一种称为“多平面视差约束”的三视角约束方法把图像序列中的每个像素点区分成背景区域和运动目标区域。该方法是在“平面和视差”框架的基础上提出来的,克服了之前几何约束方法存在的视差问题,而且不需要固定的参考平面。同时,在相机跟随目标相同方向移动时,将极线约束的面退化问题简化为线退化问题。实验结果证明了该方法的优越性。
This article proposes a method for the motion segmentation using a moving camera. It classifies each image pixel in the image sequence as the background or the motion regions by applying a three-view constraint called the "parallax-based multiplanar constraint." The method is derived from the "Plane+Parallax" framework, it overcomes the problem of the previous geometry constraint and does not require the reference plane to be constant across multiple views. Meanwhile, the method modifies the surface degradation to the line degradation to detect the motion objects followed by a moving camera in the same direction. Experiments show the superiority of our method.
地面运动目标检测在计算机视觉和视频处理方面有着非常重要的应用.移动相机下的每个像素点本身都有二维运动,这会造成强烈的视差,这就是地面运动目标分割技术的主要虚警来源.文献[1]和文献[2]介绍了一些常见的检测方法,这些方法或多或少都存在不足.在此基础上,笔者提出一种新的三视图约束方法,在分割运动目标过程中克服了传统方法的固定诱导平面问题,并且将极线约束的“面退化”修改为“线退化”,可以更加稳定地分割强视差下的运动目标.
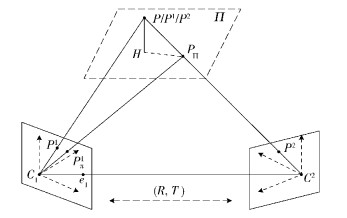
1 平面和视差框架“平面和视差”框架[3]是一种将二维的图像参数配准方法应用到三维场景中的方法. 图 1给出了平面和视差框架的几何解释. C1和C2分别是t1和t2时刻的相机中心位置,P是一个三维静态点,P1和P2分别表示P点在t1和t2时刻视场下的坐标.用3×3的旋转矩阵R和3×1的平移矢量T来表示相机在2个时刻之间发生的旋转和平移,其中平移矢量T又可以写成 (Tx, Ty, Tz).令 (x1, y1) 和 (x2, y2) 表示三维点P投影在两幅不同时刻视图中的坐标,可以通过P1=AP2来描述对应关系,其中A表示两幅视图之间对应的单应变换.
|
图 1 “平面和视差”框架的几何解释 |
这里也可以表示成J=JΠ+J1,其中JΠ表示二维图像运动的平面部分,J表示剩余的二维运动平面视差.当TZ≠0时,有
| $ {J_\Pi } = \left( {{P^2} - P_\Pi ^1} \right) $ | (1) |
| $ {J^1} = {\gamma ^1}\frac{{{T_Z}}}{{d_\Pi ^2}}\left( {{e^1} - P_\Pi ^1} \right) $ | (2) |
其中:PΠ1为由视图 2中的对应点P2变换到视图 1中的图像点 (t1时刻的视图设为参考视图),dΠ2为第2个相机的中心到参考平面Π的垂直距离,e1为极点,γ1用来衡量点P的三维形状.
|
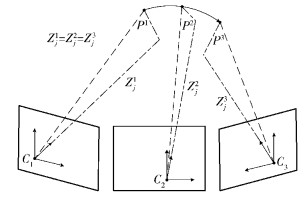
图 2 基于视差的多平面约束的退化情况 |
静态背景中2个点的平面视差的位移矢量为Jj1和Jr1,它们的相关投影结构γj1/γr1可以表示为
| $ \frac{{\gamma _j^1}}{{\gamma _{\rm{r}}^1}} = \frac{{{{\left( {\mathit{\boldsymbol{J}}_j^1} \right)}^{\rm{T}}}{{\left( {\Delta P_\Pi ^1} \right)}_ \bot }}}{{{{\left( {\mathit{\boldsymbol{J}}_{\rm{r}}^1} \right)}^{\rm{T}}}\left( {\Delta P_\Pi ^1} \right)_ \bot ^j}} $ | (3) |
Pj1和Pr1是静态背景中2个点的图像位置,ΔPΠ1=PΠ, j1-PΠ, r1,这个矢量连接了视图 2中对应点歪曲的位置,v⊥表示一个垂直于v的矢量.
极点是静止时,有
| $ \frac{{\gamma _j^1}}{{\gamma _{\rm{r}}^1}} = \frac{{{{\left( {\mathit{\boldsymbol{J}}_j^1} \right)}^{\rm{T}}}{{\left( {\Delta P_\Pi ^1} \right)}_ \bot }}}{{{{\left( {\mathit{\boldsymbol{J}}_r^1} \right)}^{\rm{T}}}{{\left( {\Delta P_\Pi ^1} \right)}^j}}} = AB/AC $ | (4) |
当视差矢量几乎平行时,极点无法估计.但是,AB/AC这个相关结构仍旧可以计算得到.
上述方法称为“模型视差约束”,它直接把2个点的相对投影结构与它们各自的视差位移联系到一起,而不需要计算相机参数和极点[4].
给定静态背景中2个点在3个不同时刻视图中的位移矢量,那么必须满足下面的刚性视差约束:
| $ \frac{{{{\left( {\mathit{\boldsymbol{J}}_j^1} \right)}^{\rm{T}}}{{\left( {\Delta P_\Pi ^1} \right)}_ \bot }}}{{{{\left( {\mathit{\boldsymbol{J}}_{\rm{r}}^1} \right)}^{\rm{T}}}\left( {\Delta P_\Pi ^1} \right)_ \bot ^j}} - \frac{{{{\left( {\mathit{\boldsymbol{J}}_j^2} \right)}^{\rm{T}}}{{\left( {\Delta P_\Pi ^2} \right)}_ \bot }}}{{{{\left( {\mathit{\boldsymbol{J}}_{\rm{r}}^2} \right)}^{\rm{T}}}\left( {\Delta P_\Pi ^2} \right)_ \bot ^j}} = 0 $ | (5) |
刚性视差约束不需要估计相机参数,提高了动目标分割的精度,但是它假设了参考平面在3个视图中是一致的,而实际上这无法保证.所以刚性视差约束在实际的应用中是比较难成立的.
3 多平面视差约束设Pj=(Xj, Yj, Zj) 是一个三维静态点,它在3个不同时刻的投影坐标分别为Pj1=(Xj1, Yj1, Zj1),Pj2=(Xj2, Yj2, Zj2),Pj3=(Xj3, Yj3, Zj3).另有一个三维静态点Pr=(Xr, Yr, Zr) 作为参考点,且在3个时刻的对应坐标分别为Pr1=(Xr1, Yr1, Zr1),Pr2=(Xr2, Yr2, Zr2),Pr3=(Xr3, Yr3, Zr3).根据第1节可以得到
| $ \left. \begin{array}{l} \gamma _j^1 = \frac{{H_j^1}}{{Z_j^1}}\\ \gamma _{\rm{r}}^1 = \frac{{H_{\rm{r}}^1}}{{Z_{\rm{r}}^1}} \end{array} \right\} $ | (6) |
由于点Pr是参考点,γr1是不变的.令γr1=α1,α1对所有像素点来说都是一个常数.这样,式 (6) 可以改写为
| $ \frac{{\gamma _j^1}}{{\gamma _{\rm{r}}^1}} = \frac{{H_j^1}}{{{\alpha _1}Z_j^1}} $ | (7) |
对于三维点Pj1,有
| $ H_j^1 = \mathit{\boldsymbol{v}}_1^{\rm{T}}P_j^1 - 1 $ | (8) |
根据式 (7) 和式 (8),再结合相机模型得到
| $ \frac{1}{{Z_j^1}} = \mathit{\boldsymbol{v}}_1^{\rm{T}}{K^{ - 1}}P_j^1{\alpha _1}\frac{{\gamma _j^1}}{{\gamma _{\rm{r}}^1}} $ | (9) |
其中K为相机的内参.令r2, 1表示旋转矩阵R2, 1的第3行,t2, 1表示平移矢量T2, 1的第3组.点Pj1的三维深度可以通过Pj2=R2, 1Pj1+T2, 1与Pj2联系到一起,即
| $ Z_j^2 = {r_{2,1}}P_j^1{t_{2,1}} $ | (10) |
结合式 (9) 可以得到
| $ \frac{1}{{Z_j^1}} = \frac{{{r_{2,1}}{K^{ - 1}}P_j^1}}{{Z_j^2}} + \frac{{{t_{2,1}}}}{{Z_j^1Z_j^2}} $ | (11) |
最后可以得到
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{v}}_1^{\rm{T}}{K^{ - 1}}P_j^1 - {\alpha _1}\frac{{\gamma _j^1}}{{\gamma _{\rm{r}}^1}} = \left( {\mathit{\boldsymbol{v}}_2^{\rm{T}}{K^{ - 1}}P_j^2 - {\alpha _2}\frac{{\gamma _j^2}}{{\gamma _{\rm{r}}^2}}} \right) \times }\\ {\left( {\left( {{r_{2,1}} + {t_{2,1}}\mathit{\boldsymbol{v}}_1^{\rm{T}}} \right){K^{ - 1}}P_j^1 - {t_{2,1}}{\alpha _1}\frac{{\gamma _j^1}}{{\gamma _{\rm{r}}^1}}} \right)} \end{array} $ | (12) |
改写成矩阵形式并化简可以得到:
| $ \left[ {\begin{array}{*{20}{c}} {P_j^2} & {\frac{{\gamma _j^2}}{{\gamma _{\rm{r}}^2}}} \end{array}} \right]{\mathit{\boldsymbol{N}}_{4 \times 4}}\left[ {\begin{array}{*{20}{c}} {P_j^1}\\ {\frac{{\gamma _j^1}}{{\gamma _{\rm{r}}^1}}} \end{array}} \right] = 0 $ | (13) |
其中:γj1/γr1为t1时刻视图到t2时刻视图的相对投影结构,γj2/γr2为t2时刻视图到t3时刻视图的相对投影结构,N为4×4的矩阵.多平面视差约束可以在不需要计算任何相机参数的情况下给出三视角视图的映射结构.
图 2所示为多平面视差约束条件下的面退化情况.
如图 2所示,P1、P2和P3分别为某一空间点P在3个时刻的对应相机坐标系里面的坐标,C1、C2和C3分别表示为对应的3个时刻的相机中心,且Zj1=Zj2=Zj3.根据前面的公式推导,可以得到
| $ \mathit{\boldsymbol{v}}_2^{\rm{T}}{K^{ - 1}}P_j^2 - {\alpha _2}\frac{{\gamma _j^2}}{{\gamma _k^2}} = \mathit{\boldsymbol{v}}_1^{\rm{T}}{K^{ - 1}}P_j^1 - {\alpha _1}\frac{{\gamma _j^1}}{{\gamma _k^1}} $ | (14) |
再结合相机模型,可以得到
| $ Z_j^1 = {r_{2,1}}P_j^1 + {t_{2,1}} $ | (15) |
由于Zj1=Zj2=Zj3,式 (15) 为恒等式,即此时无法检测出运动目标,发生线退化.但是发生线退化的条件非常苛刻,一般可以忽略.用线退化来代替面退化是多平面视差约束优越性的集中体现.
4 多平面视差约束的应用相机移动状态下的地面运动目标分割主要步骤为:估计单应变换和多平面视差约束的参数;获得平面残差图像并图像分割出运动目标;通过目标跟踪算法跟踪兴趣目标.
特征点匹配采用的是KLT (Kanade-Lucas-Tomasi) 算法[5].单应变换参数的估计采用Okade M[1]等提出的方法.设图像序列为{It+i|i=-Δ, …, 0, …, Δ},Δ是时间窗口的大小.通过单应性矩阵可以把It+i变换成It.然后通过背景更新算法获得平面残差图像,再通过阈值Th获得平面残差的二值图像.从图像序列中以τ为时间间隔选取3幅图像,通过对应特征点估计多平面视差约束的参数. N由奇异值分解获得.残差图像二值化后的运动区域的像素可以由密集光流[6]获得.这里定义一个代数误差函数:
| $ {d_{{\rm{pa}}}} = \left[ {\begin{array}{*{20}{c}} {P_j^2} & {\frac{{\gamma _j^2}}{{\gamma _{\rm{r}}^2}}} \end{array}} \right]{\mathit{\boldsymbol{N}}_{4 \times 4}}\left[ {\begin{array}{*{20}{c}} {P_j^1}\\ {\frac{{\gamma _j^1}}{{\gamma _{\rm{r}}^1}}} \end{array}} \right] $ | (16) |
设thpa是一个视差阈值.当dpa>thpa时,该像素就属于运动目标区域,反之就是在背景区域.
5 实验结果分析 5.1 定性分析图 3来自于一段航拍视频,这段视频命名为“视频1”.参数Δ=30,τ=5,Th=0.2,thpa=0.8. 图 3(a)为第70、75、80帧原始图像;图 3(b)为多平面视差约束分割结果.由结果可以看出,多平面视差约束可以有效分割出运动目标.

|
图 3 “视频1”运动目标检测结果 |
图 4来自于实验室自行拍摄的一段视频,命名为“视频2”.参数Δ=40,τ=4,Th=0.2,thpa=0.8. 图 4(a)为第386、390、394帧原始图像;图 4(b)为多平面视差约束分割结果.由结果可以看出,在有强烈视差的条件下多平面视差约束也可以有效分割出运动目标.

|
图 4 “视频2”运动目标检测结果 |
为了定量地说明多平面视差约束方法的优越性,引入探测率R(t) 和准确率P(t).手动标定视频中目标真实的像素集合,如图 5所示,采用与目标轮廓相似的多边形作为目标真实像素集合.

|
图 5 标记目标真实像素集合 |
设Φgt为目标真实像素的集合,Φdt为分割后的目标像素集合.探测率和准确率的定义分别为
| $ R\left( t \right) = \frac{{N\left( {\mathit{\Phi }_{\rm{g}}^t \cap \mathit{\Phi }_{\rm{d}}^t} \right)}}{{N\left( {\mathit{\Phi }_{\rm{g}}^t} \right)}} $ | (17) |
| $ P\left( t \right) = 1 - \frac{{N\left( {\mathit{\bar \Phi }_{\rm{d}}^t \cap \mathit{\Phi }_{\rm{g}}^t} \right)}}{{N\left( {\mathit{\Phi }_{\rm{d}}^t} \right)}} $ | (18) |
R(t) 和P(t) 都在0~1之间,且这2个参数越大,运动分割方法越好.
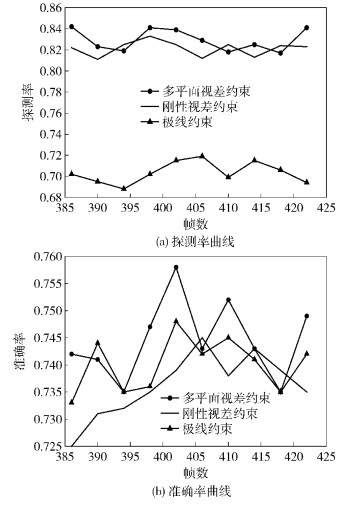
笔者选取了极线约束和刚性视差约束来与多平面视差约束进行比较. 图 6为“视频2”的探测率和准确率曲线.
由图 6(a)可以看出,极线约束的探测率明显低于另外2种方法.由于刚性视差约束和多平面视差约束都考虑到了视差问题,所以探测率较高.但从平均值来看,多平面视差约束方法还是要略高于刚性视差约束方法的,所以,所提出的多平面视差约束方法在探测率方面优于另外2种方法.
|
图 6 “视频2”的探测率和准确率曲线 |
由图 6(b)可以看出,3种方法的准确率是比较接近的.但是从平均值以及峰值来看,多平面视差约束的准确率明显优于另外2种方法.
6 结束语笔者在“平面和视差”框架的基础上提出了一种新的多平面视差约束地面运动目标分割方法,它可以有效地去除视差的影响,并且将面退化情况简化为线退化.实验结果表明,多平面视差约束可以有效地检测出移动背景下的运动目标,而且相比现有的方法,可以部分提高相机移动状态下运动目标检测的探测率和准确率.
| [1] | Okade M, Biswas P K. A novel moving object segmentation framework utilizing camera motion recognition for H.264 compressed videos [J]. Journal of Visual Communication & Image Representation, 2016, 36:199-212. |
| [2] | Sun Bin, Min Chaobo, Zhang Junju, et al. A method for moving objects segmentation based on human vision perception in infrared video[C]//International Conference on Digital Image Processing. International Society for Optics and Photonics. [S.l.]:[s.n.], 2013:27-34. |
| [3] | Irani M, Anandan P. A unified approach to moving object detection in 2D and 3D scenes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1998, 20(6): 577–589. doi: 10.1109/34.683770 |
| [4] | Kumar R, Anandan P, Hanna K. Direct recovery of shape from multiple views:a parallax based approach[C]//IAPR International Conference on Pattern Recognition, 1994. Vol. 1-Conference A:Computer Vision & Image Processin g. [S.l.]:IEEE, 1994:685-688. |
| [5] | Lucas B D, Kanade T. An iterative image registration technique with an application to stereo vision[C]//International Joint Conference on Artificial Intelligence. Morgan Kaufmann Publishers Inc. 1981:674-679. |
| [6] | Tomasi C. Detection and tracking of point features[J]. Technical Report, 1991, 9(21): 9795–9802. |


