针对冗余特征判定难题,分析了特征和特征之间的相关性以及特征和目标值之间相关性的联系,给出了判定冗余特征的准则,在此基础上给出了近似冗余特征的定义,并提出了一种基于冗余分析的特征选择算法。算法分2步去除无关特征和冗余特征。实验结果表明,所提出的特征选择算法能有效降低特征维数,提高预测准确率。
Aiming at the problem of redundant feature identification, this article analyzes the internal relationship between two kinds of correlation (correlation between feature and feature, correlation between feature and target value) and provides criterions for redundant feature determination. Approximate redundant feature is defined and a feature selection method based on redundancy is presented thereafter. The algorithm is divided into two steps to remove irrelevant features and redundant features respectively. Simulatios demonstrate that the proposed feature selection algorithms can effectively reduce feature dimension, and improve the accuracy.
随着大数据时代的到来,数据量和数据维数日趋庞大,必然会引起维数灾难[1].特征选择能有效降低特征维数,从原始特征集中提取特征子集,去除冗余特征和无关特征,实现特征维数的有效缩减,提高后续数据处理的效率和预测准确率[2].近年来,特征选择算法在模式识别[3]、机器学习[4]和医疗[5]等领域得到了广泛的应用,也取得了很多成果[6].但目前的方法都没有从相关特征中清楚地界定冗余特征,不同算法判定冗余特征的标准也不同.大多数研究者都从2个特征的相关性着手判定冗余性,极少关注2种相关性之间的内在联系,而弄清楚它们之间的联系对有效去除冗余特征有重要的意义.笔者通过分析2种相关性之间的联系,给出了判定冗余特征的准则,在此基础上定义了近似冗余特征,并提出了一种基于冗余分析的特征选择算法.此算法使用Pearson相关系数作为相关评价标准,分2步分别去除无关特征和冗余特征.实验采用局部加权线性回归 (LWLR,locally weighted linear regression) 和多项式算法评估所选择的特征子集,实验结果验证了笔者所提算法的有效性.
1 特征相关和特征冗余 1.1 特征相关特征选择就是一个寻找相关特征和冗余特征的过程,虽然已有很多研究成果确定了冗余特征的存在,并验证了它的作用[2],但少有人对2种相关性做出分析,进而从相关特征中有效的分离出冗余特征.
早在1994年,John,Kohavi和Pfleger[7]就把特征分为了3类:强相关、弱相关和无关特征.假设特征集为S,Fi为第i个特征,Mi = S-{Fi},定义描述如下.
定义1 (强相关) 一个特征Fi 为强相关的,当且仅当P(Y|Fi, Mi) ≠ P(Y|Mi).
定义2 (弱相关) 一个特征Fi为弱相关的,当且仅当P(Y|Fi, Mi) = P(Y|Mi),且
定义3 (无关) 一个特征Fi 为无关的,当且仅当∀M′i⊆Mi, P(Y|Fi, M′i) = P(Y|M′i).
可以看出,强相关特征在最优特征集中不可缺少,不能被移除.弱相关特征对最优特征集来说,并不总是必需的,有时可能不需要.而无关特征对最优特征集没有必要,可直接移除,不会对准确率有任何影响. Yu和Liu认为[8],弱相关特征可分为弱相关冗余特征和弱相关非冗余特征.但弱相关特征中哪些特征是冗余的,哪些不是,很难做出判断,因此亟需一种判定冗余特征的准则.
1.2 判定冗余特征的准则笔者使用Pearson相关系数作为评价特征相关性的标准,为方便下面描述,首先区分2种相关性. F-相关是指2个特征Fi和Fj(i≠j) 之间的相关性,用ρi, j表示;Y-相关是指特征Fi和目标值y之间的相关性,用ρi, y表示.通常来说,ρi, y值越大,说明特征Fi包含的关于y的信息量越大,反之越小;ρi, j(i≠j) 值越大,说明2个特征之间的相关性越强,反之越弱.
现实中很难判断2个特征是否完全相关,故很难准确定位冗余特征.因此,研究者们转向判定近似冗余特征,即若2个特征相关性很高,则其中1个是近似冗余的.下面分析4种极值情况下特征Fi的冗余性,并给出判定冗余特征的准则. 4种情况如表 1所示. Big是指很大,接近相关性的最大值,small是指很小,接近相关性的最小值. 2个相关特征Fi和Fj(i≠j),ρj, y≥ρi, y.
|
|
表 1 Y-相关和F-相关分布 |
情况1 ρi, y值很大,说明特征Fi包含的关于y的信息量很大.而ρi, j值很大,说明Fi和Fj之间的相关性很强,这种情况下,若ρi, j=1,则Fi和Fj完全相关,Fi是冗余的;若ρi, j≠1,则很难直接确定Fi的冗余性.
情况2 ρi, j值很小,说明Fi和Fj之间的相关性很弱,Fj并不能完全替代Fi,这时无论ρi, y值有多大,特征Fi都不是冗余特征.
情况3 ρi, y值很小,说明Fi包含的关于y的信息量很少,而ρi, j值很大,说明Fi和Fj之间的相关性很强,这时Fi极有可能是冗余的,ρi, j值越大,这种可能性就越大.
情况4 同情况2,ρi, j值很小,说明Fi和Fj间的相关性很小,这时无论ρi, y值有多大,特征Fi都不是冗余特征.
通过以上4种情况的分析,可以得出判定特征Fi冗余性的准则:
1) 在ρi, y值很大的情况下,即使ρi, j值很大,特征Fi也有可能是非冗余的;
2) 在ρi, j值很小的情况下,不管ρi, y值有多大,特征Fi都不是冗余特征.
2 特征选择算法 2.1 定义近似冗余特征根据1.2节判定冗余特征的准则,笔者给出了近似冗余特征的定义,为后续近似冗余特征的判定和特征选择算法的实施奠定了基础.
假设S为某一原始特征集,计算S中所有特征ρi, y,其最大值记为ρmax.
定义4(近似冗余特征) 2个相关特征Fi和Fj(i≠j),ρj, y≥ρi, y.
1) 当ρmax-ρi, y≤α(0 < α < 0.1) 成立时,特征Fi是近似冗余的,即Fj能近似替代Fi (Fj中包含了大部分Fi关于y的信息),当且仅当ρi, j>ρmax;
2) 当ρmax-ρi, y>α(0 < α < 0.1) 成立时,特征Fi是近似冗余的,即Fj能近似替代Fi (Fj中包含了大部分Fi关于y的信息),当且仅当ρi, j>(ρ+ρi, y)/2,其中
定义4根据1.2节判定冗余特征的2条准则,分2种情况定义了近似冗余特征,若特征Fi的Y-相关值ρi, y与ρmax很接近 (相差不超过0.1),说明ρi, y比较大,即特征Fi包含了较多的关于y的信息,这时除非ρi, j很高 (ρi, j>ρmax),否则并不认为Fi是近似冗余特征.若特征Fi的Y-相关值ρi, y与ρmax不是很接近 (定义4的2)),就把近似冗余特征的门限值设置得低一些 (ρi, j>(ρ+ρi, y)/2,而 (ρ+ρi, y)/2 < ρmax).
有些特征虽与y的相关性小 (ρi, y很小),但它和其他特征的相关性也很小 (ρi, j很小),说明这样的特征虽包含y的信息量不大,但别的特征并不能替代它,这样的特征也是非冗余的.把这种情况加到定义4中可得下面的扩展定义.扩展定义中,通过设置参数β,保留了ρi, j很小的特征Fi.
扩展定义 (近似冗余特征)2个相关特征Fi和Fj(i≠j),ρj, y≥ρi, y
1) 当ρmax-ρi, y≤α(0 < α < 0.1) 成立时,特征Fi是近似冗余的,即Fj能近似替代Fi (Fj中包含了大部分Fi关于y的信息),当且仅当ρi, j>ρmax;
2) 当ρmax-ρi, y>α(0 < α < 0.1) 成立时,特征Fi是近似冗余的,即Fj能近似替代Fi (Fj中包含了大部分Fi关于y的信息),当且仅当ρi, j>(ρ+ρi, y)/2,且ρi, j>β,β为一个用户自定义的参数.
2.2 算法基于以上对相关性和冗余性的分析和定义,笔者提出了一种基于冗余分析的扩展特征选择 (EFSBR,extended feature selection based on redundancy) 算法.算法描述如算法1所示.
EFSBR算法分2步实现.
1) 去除无关特征 (行1).首先计算原始特征集中每个特征Fi的Y-相关值ρi, y,如果ρi, y>γ,则认为Fi不是无关特征,加入特征集Slist,其中γ为去除无关特征的门限值,需要用户预先设定,同时计算所有特征Y-相关值的平均赋给参数e.然后把Slist中的特征按照ρi, y值降序排列 (行2).
2) 去除近似冗余特征 (第3~17行).首先获取Slist中最左端的第1个特征Fj(第3行),此特征的ρj, y是所有特征中最大的 (ρmax).然后获取Slist中Fj右侧的第1个特征Fi(第5行),分2种情况判断Fi是否为近似冗余特征,直到Slist中最后1个Fi比较完毕为止.第1轮基于Fj的特征过滤结束后,EFSBR算法将选择新的Fj(当前Fj右侧的第1个特征)(行16) 作为新的参考特征进行下一轮特征过滤,直到没有新的Fj可选择为止.
算法1 EFSBR算法
输入:S(F1, …, Fn, Y)
γ, α, β %用户预先设定的参数
输出:Sbest
1 对每个特征Fi,计算其Y-相关值ρi, y,如果ρi, y>γ,则填加Fi到集合Slist,同时计算所有特征Y-相关的平均值
2 把集合Slist中的特征按照ρi, y值降序排列
3 Fj= getFirstElement (Slist)
4 do begin %去除近似冗余特征
5 Fi= getNextElement (Slist, Fj)
6 if (Fi < >NULL)
7 do begin
8 if (ρmax-ρi, y≤α)
9 if (ρi, j>ρmax)
10 从Slist中移除Fi
11 else
12 if (ρi, j>(e+ρi, y)/2 & & ρi, j>β)
13 从Slist中移除Fi
14 Fi= getNextElement (Slist, Fi)
15 end until (Fi == NULL)
16 Fj= getNextElement (Slist, Fj)
17 end until (Fj == NULL)
18 Sbest = Slist
下面分析EFSBR算法的时间复杂度. EFSBR算法的计算量主要集中在计算ρi, y和ρi, j上,假设某特征集有n个特征,去除无关特征的时间复杂度是线性的O(n).去除近似冗余特征的时间复杂度最坏的情况 (没有近似冗余特征) 为O(n2),最好的情况 (除第1个参考特征外,其余n-1个都是近似冗余特征) 为O(n).
3 实验和分析实验分别使用2种不同的判断近似冗余特征的标准:定义4及其扩展定义,分别记为基于冗余分析的特征选择 (FSBR,feature selection based on redundancy) 算法和EFSBR算法.为了验证这2种算法的有效性和效率,实验在3个真实数据集和3个公共数据集上同目前经典的特征选择算法最大相关最小冗余 (MRMR,maximum relevance minimum redundancy) 和基于相关性的快速滤波 (FCBF,fast correlation based filter) 算法进行比较.为了比较的公平性,MRMR和FCBF算法的相关性评价标准使用的是Pearson相关系数. MRMR算法使用的是除法最优化,实验证明,除法最优化比减法最优化具有更优的性能[6].实验的运行环境为Intel (R) Core (TM) i5-4690 CPU 3.5 GHz,8 GB内存,Matlab2016.
3.1 数据集和评价标准真实数据集来自某公司1年的工业测试数据,包括制冷能力测试集 (FCDS,freezing capacity data set)、负载温度回升测试集 (TRLTRDS,temperature rise of load time respectively data set) 和耗电量测试集 (ECDS,energy consumption data set).公共数据集来自加利福尼亚大学欧文分校 (UCI,university of California Irvine) 机器学习库,有威斯康星乳腺癌 (预后性症状)(BCW (P),breast cancer Wisconsin (prognostic))、帕金森监护 (PT,Parkinsons telemonitoring)、学生成绩 (SP,student performance). PT数据集的预测目标有motor帕金森综合评分量表 (UPDRS,unified Parkinson diease rating scale) 和total UPDRS,实验预测的是total UPDRS. BCW (P) 和SP特征集中的文本数据都已处理为数值数据.数据集的信息描述如表 2所示.
|
|
表 2 数据集信息描述 |
实验使用LWLR和多项式算法完成特征子集的评估.多项式算法使用的是2次多项式 (相比其他幂次,2次多项式在该实验中的拟合效果最好).为防止过 (欠) 拟合,进行了正则化处理.
不同特征选择方法的性能通过下面3种标准评价:
1) 所选择的特征维数;
2) 不同特征选择算法运行的时间;
3) 不同算法选择的特征子集的预测性能.
实验使用相对误差 (RAE,relative absolute error) 和均方根误差 (RMSE,root mean square error) 来评价所选择的特征子集的性能,RAE反映预测的可信程度,记为A,而RMSE衡量预测值与真实值之间的偏差,记为R,分别表示为
| $ A = \frac{1}{m}\sum\limits_{i = 1}^m {\frac{{\left| {{y_i}-{{\hat y}_i}} \right|}}{{{y_i}}}} {\rm{ \times }}100\% $ | (1) |
| $ R = \sqrt {\frac{1}{m}\sum\limits_{i = 1}^m {{{\left( {{y_i}-{{\hat y}_i}} \right)}^2}} } $ | (2) |
其中:yi为实际值,ŷi为预测值,m为测试集中的样本数.
实验中,所有数据集的参数β取值为0.4.通常,相关系数按照相关性强弱可划分为3级:|ρ| < 0.4为低度相关,0.4≤|ρ| < 0.7为显著相关,0.7≤|ρ| < 1为高度线性相关.因此,对Y-相关值较小的特征,建议参数β的取值为0.4.
实验中,所有数据集的参数γ取值为0.在没有先验知识的情况下,相关性门限值γ建议取0,即当ρi, y>γ时,认为特征Fi和y是相关的;反之,是不相关的.
3.2 实验结果和分析由于样本数较少,实验中训练集使用留一交叉验证 (LOOCV,leave one out cross validation) 确定最优参数,测试集使用LOOCV预测结果,最终取LOOCV平均误差. 3个真实数据集的α取值均为0.13,3个UCI数据集α的取值分别为0.04、0.09和0.09.
图 1显示了6个数据集使用特征选择算法前后特征维数的变化.可以看出,4种特征选择算法均能有效降低特征维数.
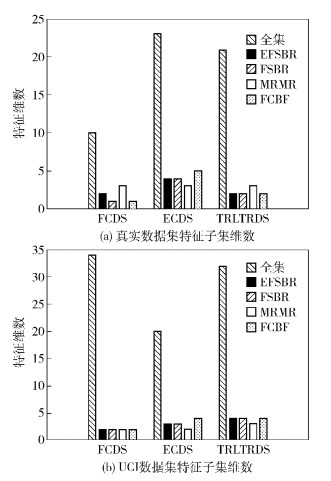
|
图 1 特征子集维数 |
表 3和表 4分别显示了使用多项式算法和LWLR算法的LOOCV平均RAE误差和平均RMSE误差.由于篇幅有限,仅把6个数据集的RMSE平均LOOCV误差分别列在了表 3和表 4的最后1行,其中,每个数据集的最小误差已加粗显示.由表 3和表 4可以看出,EFSBR算法的有效性体现在3个方面:1) 能有效降低RAE误差,降幅最大为26.8%;2) RAE误差均低于其他算法 (除FCDS-多项式外);3) EFSBR算法选出的特征子集对应的平均RMSE误差最小,其次为FSBR、FCBF和MRMR算法. FSBR算法在FCDS上的结果不如EFSBR算法,但在ECDS和TRLTRDS上,FSBR算法的RAE误差均低于其他算法.进一步验证了设置参数β的必要性.
|
|
表 3 多项式算法的平均RAE误差 (%) 和RMSE误差 |
|
|
表 4 LWLR算法的平均RAE误差 (%) 和RMSE误差 |
针对相同的特征集,LWLR算法比多项式算法预测的RAE误差要小一些.这说明,对某个特征集来说,要得到最好的预测结果,必须找到与之匹配的学习算法.
针对FCDS和ECDS数据集,实验使用多项式算法分析了相关和冗余的关系,结果如表 5所示.其中,“{4}”为特征的下标,即第4个特征,“变化”为以当前特征集为基准准确率的变化.由表 5可以看出:1) 以{4}为当前特征集,增加特征F6或F10后准确率均提高,验证了1.2节中的近似冗余特征准则1);2) 以{4, 6}为当前特征集,增加特征F2后准确率提高;以{8, 4}为当前特征集,增加F13后准确率提高,验证了1.2节中的近似冗余特征准则2).
|
|
表 5 相关和冗余的关系 |
表 6显示了4种特征选择算法在6个数据集上多项式算法5次运行时间的平均.由运行结果可以看出,EFSBR、FSBR和FCBF算法的平均运行时间近似,而MRMR算法的平均运行时间最长,这主要是因为MRMR算法选择每个特征都要经过|Slist|2次的计算,导致计算量比其他算法要大.
|
|
表 6 不同选择算法在6个数据集上的运行时间 |
2.1节近似冗余特征的定义中涉及参数α,为验证α对EFSBR和FSBR算法性能的影响,笔者使用多项式算法在6个数据集上进行了实验,实验中保持参数β=0.4不变,随着参数α∈[0.01, 0.1]的变化,EFSBR和FSBR算法选出的特征子集取得最小误差时参数α的取值范围如图 2所示.由图 2可以看出,不同数据集获得最小误差时的α的取值范围并不统一,但有重叠,大约在[0.03, 0.09]范围内.因为对于每个原始数据集,能近似此原始数据集的特征子集是确定的,可能为1个,也可能为多个 (误差都相同,但特征维数不同),特征选择算法的目标就是找到其中1个特征子集.但不同数据集的近似最优特征子集的维数各异,且不同数据集的Y-相关值的分布各异,从而导致数据集在取得最小误差时α的取值范围各异.因此,针对不同数据集,α的取值并不统一.建议α的取值可从0.03或0.04开始尝试,一直到0.10,然后从中选出使预测误差最小的特征子集对应的α值.

|
图 2 6个数据集上FSBR和EFSBR算法取得最小误差时参数α的取值范围 |
分析了2种相关性 (F-相关和Y-相关) 之间的关系,在此基础上给出了判定冗余特征的准则,从而给出了近似冗余特征的定义,并提出了一种基于冗余分析的特征选择算法FSBR及其扩展算法EFSBR.将该算法和MRMR、FCBF算法在3个真实数据集和3个公共数据集上进行了比较,实验结果验证了EFSBR和FSBR算法的效率和有效性. Filter和Wrapper[2]算法相结合选择最优特征集是下一步的研究方向.
| [1] | Hastie T, Tibshirani R, Friedman J. The elements of statistical learning[M]. [S. l.]:Springer, 2001. |
| [2] | Kohavi R, John G H. Wrappers for feature subset selection[J]. Artificial Intelligence, 1997, 97(1-2): 273–324. doi: 10.1016/S0004-3702(97)00043-X |
| [3] | Ding Shifei, Zhu Hong, Jia Weikuan, et al. A survey on feature extraction for pattern recognition[J]. Artificial Intelligence Review, 2012, 37(3): 169–180. |
| [4] | Robnik M, Ikonja M, Kononenko I. Theoretical and empirical analysis of ReliefF and RReliefF[J]. Machine Learning, 2003, 53(1): 23–69. |
| [5] | Zagoruiko N G, Kutnenko O A, Borisova I A, et al. Feature selection in the task of medical diagnostics on microarray data[J]. Russian Journal of Genetics:Applied Research, 2015, 5(4): 330–334. doi: 10.1134/S2079059715040164 |
| [6] | Ding Chris, Peng Hanchuan. Minimum redundancy feature selection from microarray gene expression data[C]//Bioinformatics Conference, 2003. Stanford:IEEE, 2003:523-528. |
| [7] | John G H, Kohavi R, Pfleger K. Irrelevant features and the subset selection problem[J]. Machine Learning Proceedings, 1998: 121–129. |
| [8] | Yu Lei, Liu Huan. Efficient feature selection via analysis of relevance and redundancy[J]. Journal of Machine Learning Research, 2004, 5(12): 1205–1224. |



