2. 电子科技大学 中山学院, 广东 中山 528402
提出一种自适应储能系统控制方法,对智能电网中电动汽车的动态无线充电负荷进行调节。该方法在系统代价函数中联合考虑电网侧功率的变化率和充放电对电池寿命的影响,采用自适应动态规划算法,通过在线神经网络训练,估计并最优化系统长期代价,从而得到近似最优的储能系统控制策略。仿真结果表明,该方法能有效降低电网侧功率的斜率,使负荷更加平稳,同时延长储能系统中电池的寿命。
2. Zhongshan Institute, University of Electronic Science and Technology of China, Guangdong Zhongshan 528402, China
An adaptive energy storage system control method was proposed to regulate the loads caused by electric vehicle dynamic wireless charging in smart grid. The proposed method jointly considers the grid-side power ramp rate and the charging/discharging impact on a battery's life in the system cost function. Adaptive dynamic programming algorithm is used to estimate and optimize the long-term system cost through online neural network training, so that the approximate optimal control strategy for the energy storage system can be obtained. Simulation shows that the proposed method can reduce the grid-side power ramp rate stabilizing the loads and also prolong the battery's life of the energy storage system.
动态无线充电技术能使电动汽车充电更加便捷和安全[1-3],但这同时给电网带来负面冲击.大量快速行驶的汽车进入和离开无线充电系统可导致系统负荷剧烈抖动,这些高功率负荷的快速变化会给电网带来巨大冲击,严重时可造成电压畸形、频率波动等.对此,可采用电池储能系统对抖动的负荷进行缓冲[4].
针对电动汽车动态无线充电的负荷调节,采用自适应动态规划算法对电池储能系统进行控制.该算法采用在线学习方法来优化控制策略,既能减缓负荷的抖动,也能降低电池寿命的损耗.最后通过仿真实验分析控制方法的性能.
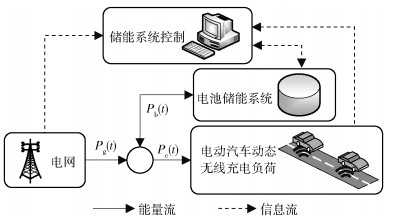
1 系统模型系统模型如图 1所示.电能发送系统沿着车道安装在马路地面下,电能接收系统安装在车底,2个系统自动相互连接,通过电磁感应传输电能.电动汽车以一定的到达率进入车道,并在车道内一边行驶一边充电,故系统总充电负荷与车道内车数有关.考虑离散时间系统控制,把时隙记为t,有t=1, 2, ….把无线充电系统的总充电功率记为Pc(t),有Pc(t)≥0.记电池储能系统的输出功率为Pb(t),Pb(t)>0为充电,Pb(t) < 0为放电.所以,Pg(t)=Pb(t)+Pc(t) 为电网侧的总功率.储能系统控制的作用就是通过获取电网、电池、负荷的信息,优化电池储能系统的充放电策略,使电网侧负荷平稳.该控制方法综合考虑2个优化目标.第1个目标是最小化电网侧功率的斜率,其公式表达为
| $ {R_{\rm{g}}}\left( t \right) = \frac{{{P_{\rm{g}}}\left( t \right) - {P_{\rm{g}}}\left( {t - 1} \right)}}{{\Delta t}} $ | (1) |
|
图 1 用于动态无线充电负荷调节的储能系统控制图 |
其中:Δt为1个时隙的时间.通常情况下,发电机的特性决定了可承受的负荷功率斜率最小和最大值,故有Rg, min≤Rg(t)≤Rg, max.若负荷功率斜率超过此范围,就会影响电网的电能质量.第2个目标是最小化电池的使用率[5],其公式表达为
| $ {L_{\rm{b}}}\left( t \right) = \frac{{\left| {{P_{\rm{b}}}\left( t \right)} \right|\Delta t}}{{{C_{\rm{b}}}{N_{\rm{b}}}}} $ | (2) |
其中:Cb为电池的设计容量;Nb为电池的设计充放电循环次数.由于Δt、Cb、Nb均为常数,故可用Lb(t)=|Pb(t)|来评估电池的使用率,有Lb, min ≤Lb(t)≤Lb, max .电池的使用率会影响电池的寿命.最后仿真实验会给出控制过程中电池寿命损耗的结果.
2 自适应动态规划算法 2.1 问题描述控制器通过观测电动汽车动态无线充电负荷和电网侧负荷来调整对电池储能系统的控制策略.记x (t) 为系统在时隙t的状态,有x(t)=(Pc(t), Pg(t-1)).记u(t) 为系统在时隙t的决策,有u(t)=Pg(t),故电池的充放电功率表示为Pb(t)=u(t)-Pc(t).记U[x(t), u(t)]为系统在时隙t的代价,其定义为
| $ U\left[ {\mathit{\boldsymbol{x}}\left( t \right),u\left( t \right)} \right] = {\omega _{\rm{g}}}{{\dot R}_{\rm{g}}}\left( t \right) + {\omega _{\rm{b}}}{{\dot L}_{\rm{b}}}\left( t \right) $ | (3) |
其中:Ṙg(t) 和
| $ J\left[ {\mathit{\boldsymbol{x}}\left( t \right)} \right] = \sum\limits_{j = 1}^\infty {{\gamma ^{j - t}}U\left[ {\mathit{\boldsymbol{x}}\left( j \right),u\left( j \right)} \right]} $ | (4) |
其中γ为折扣因子,有0≤γ≤1.当γ=0时,只考虑当前时隙代价;当γ=1时,认为所有未来时隙的代价同等重要.电池储能系统的控制目标就是得到最优的控制策略{u*(t), u*(t+1), …},从而得到最优系统长期代价J*[x(t)]=0.根据Bellman方程,时隙t的最优系统长期代价表示为
| $ {J^ * }\left[ {\mathit{\boldsymbol{x}}\left( t \right)} \right] = \mathop {\min }\limits_{u\left( t \right)} \left\{ {U\left[ {\mathit{\boldsymbol{x}}\left( t \right),u\left( t \right)} \right] + \gamma {J^ * }\left[ {\mathit{\boldsymbol{x}}\left( {t + 1} \right)} \right]} \right\} $ | (5) |
时隙t的最优控制决策为
| $ {u^*}\left( t \right) = \mathop {\arg \min }\limits_{u\left( t \right)} \left\{ {U\left[ {\mathit{\boldsymbol{x}}\left( t \right),u\left( t \right)} \right] + \gamma {J^*}\left[ {\mathit{\boldsymbol{x}}\left( {t + 1} \right)} \right]} \right\} $ | (6) |
采用传统的动态规划求解式 (6) 会面临维数灾难问题.故笔者采用自适应动态规划算法来估计并最优化系统长期代价,从而得到近似最优的控制策略.
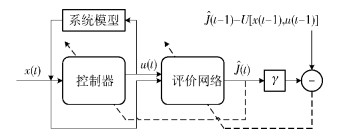
2.2 算法原理针对电池储能系统控制问题,采用自适应动态规划 (ADP,adaptive dynamic programming) 中的执行依赖启发式动态规划结构[6],其包含系统模型、控制器、评价网络,如图 2所示. 图 2中的系统模型描述电动汽车充电负荷的变化,其输入为决策u(t),输出为系统状态x(t).控制器的输入为状态x (t),输出为决策u(t).评价网络的输入为x(t) 和u(t),输出为系统长期代价估计值Ĵ (t).评价网络和控制器采用神经网络结构,并进行在线训练.评价网络训练的目标是使其输出Ĵ (t) 逼近原函数J[x(t)],故应该最小化误差函数Ec(t),其定义为
| $ \begin{array}{*{20}{c}} {{E_{\text{c}}}\left( t \right){\text{ = }}} \\ {\frac{1}{2}{{\left[ {\hat J\left( {t - 1} \right) - U\left[ {{\mathbf{x}}\left( {t - 1} \right),u\left( {t - 1} \right)} \right] - \gamma \hat J\left( t \right)} \right]}^2}} \end{array} $ | (7) |
|
图 2 自适应动态规划算法结构图 |
当式 (7) 等于0时,有
| $ \begin{array}{*{20}{c}} {\hat J\left( t \right) = U\left[ {\mathit{\boldsymbol{x}}\left( t \right),u\left( t \right)} \right]\gamma \hat J\left( {t + 1} \right) = }\\ {U\left[ {\mathit{\boldsymbol{x}}\left( t \right),u\left( t \right)} \right] + \gamma \left( {U\left[ {\mathit{\boldsymbol{x}}\left( {t - 1} \right),u\left( {t - 1} \right)} \right] + } \right.}\\ {\left. {\gamma \hat J\left( {t + 2} \right)} \right) = \cdots = \sum\limits_{j = t}^\infty {{\gamma ^{j - t}}U\left[ {\mathit{\boldsymbol{x}}\left( j \right),u\left( j \right)} \right]} } \end{array} $ |
这正是由式 (4) 定义的系统长期代价.所以,评价网络最小化误差函数Ec(t),可使Ĵ (t) 逼近原函数J[x(t)].控制器的目标是通过调整输出u(t) 使Ĵ (t) 逼近0,故其神经网络训练时应最小化误差函数Ea(t),其定义为
| $ {E_{\rm{a}}}\left( t \right) = \frac{1}{2}{\left[ {\hat J\left( t \right)} \right]^2} $ | (8) |
当式 (8) 等于0时,Ĵ (t) 有最优值0.所以,在电池储能系统控制过程中,通过在线神经网络训练可估计并最优化Ĵ (t),从而得到近似最优的控制策略.
2.3 算法实现采用反向传输 (BP,back-propagation) 神经网络实现控制器和评价网络的功能.对于一个典型的3层BP神经网络,定义X为输入向量;W1为输入层与隐藏层之间的权重矩阵;W2为隐藏层与输出层之间的权重矩阵;σ为激活函数,定义为[σ(z)]i=(1-e-zi)/(1+e-zi),i=1, …, Nh,Nh为隐藏层神经元的个数;l为学习率,有l>0.
采用梯度下降法进行神经网络训练[6].采用下标c来标记评价网络的参数和变量,评价网络的输出可表示为
| $ \hat J\left( t \right) = \mathit{\boldsymbol{W}}_{2,{\rm{c}}}^{\rm{T}}\left( t \right)\sigma \left[ {\mathit{\boldsymbol{W}}_{1,{\rm{c}}}^{\rm{T}}\left( t \right){\mathit{\boldsymbol{X}}_{\rm{c}}}\left( t \right)} \right] $ | (9) |
其中:Xc(t)=(x(t), u(t))T,Xc(t)∈R3.评价网络的权重更新公式为
| $ \Delta {\mathit{\boldsymbol{W}}_{\rm{c}}}\left( t \right) = {l_{\rm{c}}}\left( t \right)\left[ { - \frac{{\partial {E_{\rm{c}}}\left( t \right)}}{{\partial {\mathit{\boldsymbol{W}}_{\rm{c}}}\left( t \right)}}} \right] $ | (10) |
| $ {\mathit{\boldsymbol{W}}_{\rm{c}}}\left( {t + 1} \right) = \frac{{{\mathit{\boldsymbol{W}}_{\rm{c}}}\left( t \right) + \Delta {\mathit{\boldsymbol{W}}_{\rm{c}}}\left( t \right)}}{{{{\left\| {{\mathit{\boldsymbol{W}}_{\rm{c}}}\left( t \right) + \Delta {\mathit{\boldsymbol{W}}_{\rm{c}}}\left( t \right)} \right\|}_1}}} $ | (11) |
采用下标a来标记控制器网络的参数和变量,控制器网络的输出可表示为
| $ u\left( t \right) = \sigma \left( {\mathit{\boldsymbol{W}}_{2,{\rm{a}}}^{\rm{T}}\left( t \right)\sigma \left[ {\mathit{\boldsymbol{W}}_{1,{\rm{a}}}^{\rm{T}}\left( t \right){\mathit{\boldsymbol{X}}_{\rm{a}}}\left( t \right)} \right]} \right) $ | (12) |
其中:Xa(t)=xT(t),Xa(t)∈R2.控制器网络的权重更新公式为
| $ \Delta {\mathit{\boldsymbol{W}}_{\rm{a}}}\left( t \right) = {l_{\rm{a}}}\left( t \right)\left[ { - \frac{{\partial {E_{\rm{a}}}\left( t \right)}}{{\partial {\mathit{\boldsymbol{W}}_{\rm{a}}}\left( t \right)}}} \right] $ | (13) |
| $ {\mathit{\boldsymbol{W}}_{\rm{a}}}\left( {t + 1} \right) = \frac{{{\mathit{\boldsymbol{W}}_{\rm{a}}}\left( t \right) + \Delta {\mathit{\boldsymbol{W}}_{\rm{a}}}\left( t \right)}}{{{{\left\| {{\mathit{\boldsymbol{W}}_{\rm{a}}}\left( t \right) + \Delta {\mathit{\boldsymbol{W}}_{\rm{a}}}\left( t \right)} \right\|}_1}}} $ | (14) |
系统模型参数设置为:采用文献[4]的参数生成电动汽车动态无线充电负荷.在一条总长8 km的车道上连续安装无线充电板,车只要在该车道上行驶就能连续获得无线电能.设在车道上行驶的车一直以50 kW的功率进行充电,其充电时间就是在车道上的行驶时间.一辆车的长度为5 m.关于车速,考虑低速和高速2种情况.低速情况下,车速36 km/h,车与车之间的距离5 m,进入车道的车流量2 600辆/h;高速情况下,车速108 km/h,车距10 m,车流量5 000辆/h.设每个时隙的时间Δt=0.1 s,实验时间为20 min,共1.2万个时隙.自适应动态规划算法参数设置为:折扣因子γ=0.95.评价网络和控制器网络分别采用3-6-1和2-6-1结构的BP神经网络.学习率为lc=0.1和la=0.1.
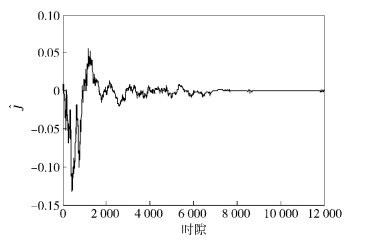
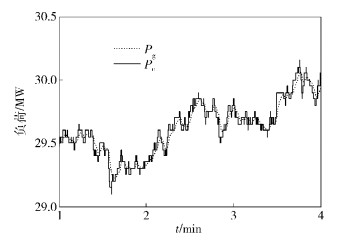
3.2 控制性能图 3为评价网络输出曲线,即近似最优系统长期代价Ĵ.可见,笔者采用的ADP算法通过在线神经网络训练,可把Ĵ收敛至最优值. 图 4给出该控制方法在低速场景下和ωg=0.9与ωb=0.1的情况下Pc和Pg的曲线.由图 4可知,电动汽车动态无线充电功率Pc的变化率十分陡峭,这是大量汽车快速进入和离开车道造成的.由于与电池使用率有关的权重ωb较小,所以该算法会控制电池频繁地进行充放电,避免电网侧功率Pg出现陡峭的变化率.
|
图 3 评价网络输出曲线 |
|
图 4 电网侧功率和动态无线充电功率 |
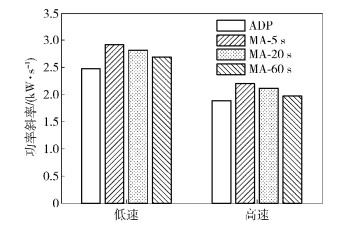
下面给出该储能系统控制方法在负荷调节和电池寿命方面的性能表现.在控制过程中采用的权重参数为ωg=0.5和ωb=0.5.对比方法为移动平均线 (MA,moving average) 方法[4].该方法在控制过程中,把时间窗口内 (5 s、20 s和60 s) 充电功率的期望值作为电网侧功率值,并没有考虑功率斜率和电池寿命的问题.由图 5可知,与MA方法相比,该ADP控制方法有效地降低电网侧功率的最大斜率.
|
图 5 电网侧功率在不同控制方法下的最大斜率 |
采用疲劳模型[2]来评估电池的寿命损耗.该模型认为每一次充放电循环都会损耗电池的寿命.电池的放电深度 (DoD,depth of discharge) 越大,该电池在失效之前的总循环次数越少.电池的寿命损耗公式[7]为
| $ Q = \sum\limits_{D = 0.01}^1 {\frac{{N\left( D \right)}}{{{N_{{\rm{ctf}}}}\left( D \right)}}} $ | (15) |
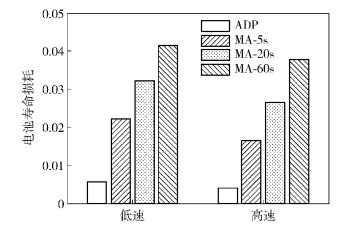
其中:D为DoD,Nctf(D) 为在某DoD下电池失效前的总循环次数[2];N(D) 为在控制过程中,在某DoD下损失的循环次数.控制结束后,可得电池的DoD曲线,再使用雨流算法[8]可计算出控制时间内的N(D).由图 6可知,该ADP控制方法能有效地降低电池的寿命损耗.
|
图 6 电池在不同控制方法下的寿命损耗 |
面向智能电网中电动汽车动态无线充电负荷的调节,提出一种自适应储能系统控制方法.构造代价函数时,综合考虑电网侧功率斜率和电池使用率,采用自适应动态规划算法,通过在线神经网络训练,估计并最优化系统长期代价,从而得到近似最优的储能系统控制策略.仿真结果表明,该方法能有效降低电网侧功率的斜率,缓冲负荷抖动,也降低电池的寿命损耗,减少电池投入成本.
| [1] | Yu Rong, Huang Xumin, Kang Jiawen, et al. An optimal replenishment strategy in energy harvesting wireless networks with a mobile charger[C]//11th International Conference on Heterogeneous Networking for Quality, Reliability, Security and Robustness. Taipei:IEEE, 2015:433-439. |
| [2] | Jeong S, Jang Y, Kum D. Economic analysis of the dynamic charging electric vehicle[J]. IEEE Transactions on Power Electronics, 2015, 30(11): 6368–6377. doi: 10.1109/TPEL.2015.2424712 |
| [3] | Kang Jiawen, Yu Rong, Maharjan S, et al. Toward secure energy harvesting cooperative networks[J]. IEEE Communications Magazine, 2015, 53(8): 114–121. doi: 10.1109/MCOM.2015.7180517 |
| [4] | Amditis A, Theodoropoulos T, Damousis Y, et al. FABRIC's approach towards the estimation of energy storage system requirements for grid impact reduction[C]//International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles. Aachen:IEEE, 2015:1-5. |
| [5] | Pan Xin, Xu Hanchen, Song Jie, et al. Capacity optimization of battery energy storage systems for frequency regulation[C]//IEEE International Conference on Automation Science and Engineering. Goteborg:IEEE, 2015:1139-1144. |
| [6] | Si Jennie, Wang Yutsung. On-line learning control by association and reinforcement[J]. IEEE Transactions on Neural Networks, 2001, 12(2): 264–276. doi: 10.1109/72.914523 |
| [7] | Schaltz E, Khaligh A, Rasmussen P O. Influence of battery/ultracapacitor energy-storage sizing on battery lifetime in a fuel cell hybrid electric vehicle[J]. IEEE Transactions on Vehicular Technology, 2009, 58(8): 3882–3891. doi: 10.1109/TVT.2009.2027909 |
| [8] | Houari A, Abbes D, Labrunie A, et al. Hybridization of electrical energy storage for intelligent integration of photovoltaics in electric networks[C]//European Conference on Power Electronics and Applications. Geneva:IEEE, 2015:1-10. |


