心电信号采集过程中容易受到基线漂移、工频和肌电等噪声的干扰。为了提高心电信号的信噪比,结合平稳小波变换,在使用小波阈值去噪法去燥过程中,提出一种有别于常用软硬阈值函数的新的阈值函数。通过分析实测数据验证新阈值函数,结果表明,该方法更加有效地抑制了心电信号中混入的基线漂移、工频和肌电噪声,且较好地保留了原始心电信号的特征。
The electrocardiogram (ECG) signal is commonly interfered by noises of baseline drift, power frequency, and electromyography, which happens during collections. To improve the signal noise ratio of ECG signals, a threshold function was proposed in the denoising process of the wavelet threshold denoising method, which combining the stationary wavelet transform. And the function is different from the usual one. The new function is verified by analyzing the measured data, it shows that the noises which is introduced in the ECG signal by the baseline drift, power frequency, and electromyography, are removed more effectively, and also the characteristics of the original ECG signal are kept better.
心电 (ECG,electrocardiogram) 信号是非常微弱的生理信号,在心电数据的采集过程中,由于呼吸、肌肉颤抖和供电环境等因素的影响,通常会使心电信号夹杂着一些噪声.噪声按来源可分为基线漂移干扰噪声、工频干扰噪声和肌电干扰噪声.为了对病人的病情进行准确的诊断,需要得到纯净的心电信号,所以对所监测到的心电信号进行噪声去除是心电监测系统首要而且必需的工作.
在阈值去噪法中阈值函数主要有2种,即软阈值法和硬阈值法.这2种方法都有各自的优缺点,软阈值法的优点是经其处理过的信号会比较光滑,缺点是重构后得到的信号幅度上有衰减,尤其是R波幅度的衰减比较明显,还会造成信号边缘模糊,进而造成信号失真;硬阈值法的优点是对原始信号的特征点进行较好的重构,缺点是经其处理的信号会产生震荡,出现伪吉布斯现象[1].
为了克服以上2种阈值法的缺陷,使去除噪声并重构后的心电信号更准确,较好地保留原始心电信号的特征,提除了一种新的阈值函数,并结合平稳小波变换最终去除工频干扰、基线漂移和肌电干扰3种噪声.
1 去噪原理分析 1.1 平稳小波变换平稳小波变换也被称为非抽样的小波变换[2],其进行分解是先对每一层上的低通及带通分解滤波器在上一层分解滤波器的基础上进行上采样,即隔点补零操作.在不同的分解层次上使用不同的分解滤波器[3],完成卷积计算后并不对细节系数和近似系数进行下采样操作,平稳小波变换的这一非抽样的特性,使得每一分解层数上的近似系数与细节系数的长度都与原始信号的长度相同,使得在重构时,每一层上的低频系数和高频系数作用于重构滤波器后直接相加可得上一层的低频系数,不需要在与重构滤波器做卷积操作之前再做上采样操作,且在每一层的重构过程中都可使用相同的滤波器[4],可有效地避免由于信号下抽样但小波基不具有平移不变性而造成重构信号产生伪吉布斯震荡的问题,弥补了传统正交小波变换的不足.
1.2 阈值法原理分析含有噪声的信号经平稳小波变换后,噪声部分主要分布在高频小波系数中,该小波系数幅值较小,数量多;而有用信号主要分布在低频小波系数中,该小波系数幅值较大,数量少,基于上述不同,选择一个合适的阈值,幅度低于该阈值的小波系数,认为其主要成分是噪声,将小波系数置零或用阈值函数进行处理;幅度高于该阈值的小波系数,认为其主要成分是有用信号,将其进行保留,之后利用处理过的所有小波系数进行重构,即可实现去噪的目的.
2 提出新阈值函数 2.1 新阈值函数新阈值函数的提出应以以下几点为依据:保证小波系数在阈值点T和-T处是连续的;尽可能地减小原小波系数S和处理后的小波系数T之间存在的偏差;使软阈值函数的导数连续,解除了软阈值函数导数不连续的局限性.且在采用实测的心电数据进行实验的过程中,发现当心电数据的个数不同时,不能只单一地采用软阈值函数或硬阈值函数,应设计一种既克服了软、硬阈值函数的缺点,并兼顾两者的优点,又能根据心电数据的个数不同而自适应变化的新的阈值函数,如式 (1) 所示.
| $ S = \left\{ \begin{array}{l} {\rm{sign}}\left( X \right)\left[ {\left| X \right| - \frac{T}{{\exp \left[ {\frac{{\sqrt {{X^2} - {T^2}} }}{N}} \right]}}} \right], \left| X \right| \ge T\\ 0, \left| X \right| < T \end{array} \right. $ | (1) |
其中N为心电数据的个数,通过分析式 (1) 可知,该阈值函数是连续的,且当|X|≥T时函数高阶可导,对于函数
| $ f\left( x \right) = {\rm{sgn}}\left( x \right)\left[ {\left| x \right| - \frac{T}{{\exp \left[ {\frac{{\sqrt {{x^2} - {T^2}} }}{N}} \right]}}} \right] $ | (2) |
当x>0且x→+∞时,有
| $ \begin{array}{*{20}{c}} {\frac{{f\left( x \right)}}{x} = \frac{{\left| x \right| - \frac{T}{{\exp \left[ {\frac{{\sqrt {{x^2} - {T^2}} }}{N}} \right]}}}}{x} = }\\ {1 - \frac{T}{{x\exp \left[ {\frac{{\sqrt {{x^2} - {T^2}} }}{N}} \right]}} \to 1} \end{array} $ | (3) |
当x < 0且x→-∞时,有
| $ \frac{{f\left( x \right)}}{x} \to 1 $ | (4) |
同时当x→∞时,有
| $ f\left( x \right) - x = {\mathop{\rm sgn}} \left( x \right)\frac{T}{{\exp \left[ {\frac{{\sqrt {{x^2} - {T^2}} }}{N}} \right]}} \to 0 $ | (5) |
所以式 (2) 是以直线y=x为渐近线的,也就是说,式 (1) 提出的函数以S=X为渐近线,当X逐渐增大时,S逐渐接近X,这样克服了采用软阈值函数时,S与X之间具有恒定偏差的缺陷,当阈值T很小,新阈值函数近似相当于硬阈值函数.
当N→∞时,有
| $ \begin{array}{*{20}{c}} {{\mathop{\rm sgn}} \left( X \right)\left[ {\left| X \right| - \frac{T}{{\exp \left[ {\frac{{\sqrt {{X^2} - {T^2}} }}{N}} \right]}}} \right] = }\\ {{\mathop{\rm sgn}} \left( X \right)\left( {\left| X \right| - T} \right)} \end{array} $ | (6) |
当N→0时,有
| $ {\mathop{\rm sgn}} \left( X \right)\left[ {\left| X \right| - \frac{T}{{\exp \left[ {\frac{{\sqrt {{X^2} - {T^2}} }}{N}} \right]}}} \right] = X $ | (7) |
式 (6) 和式 (7) 说明,当N趋于0时,新阈值函数其实相当于硬阈值函数,但它更灵活; 当N趋于无穷时,该阈值函数相当于软阈值函数.因此,可通过N的取值变化,得到合适的阈值函数.
2.2 小波函数的选取适用于心电信号处理的小波函数有symslet小波和biorthogona小波,定义相对信噪比 (SNR,signal noise ratio) 增益β即重构信号SNR和原始信号SNR的比值来作为选择小波函数的依据[5].
| $ \beta = \frac{{R\left( {y\left( n \right)} \right)}}{{R\left( {x\left( n \right)} \right)}} $ | (8) |
其中R为SNR.
通过比较发现,适用于心电信号去噪的小波函数分别为bior5.5和sym8. bior5.5的相对SNR增益更高,所以选取bior5.5作为心电信号小波分解的小波函数.
2.3 频带分析信号8层分解各尺度子带系数范围如表 1所示.
|
|
表 1 信号8层分解各尺度子带系数范围 |
人体的心电信号的频率主要分布在0.5~100 Hz之间,幅度属于微伏级.心电信号中的噪声主要有3种,基线漂移为0.05~1 Hz,工频干扰为50 Hz,肌电干扰为5~1 000 Hz.
3 实验结果所用心电数据是在人体实际测量得到的数据.
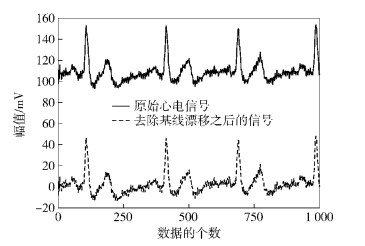
3.1 基线漂移的滤除将第8尺度上的低频系数置零可去除基线漂移干扰,如图 1所示.
|
图 1 去除基线漂移前后的对比 |
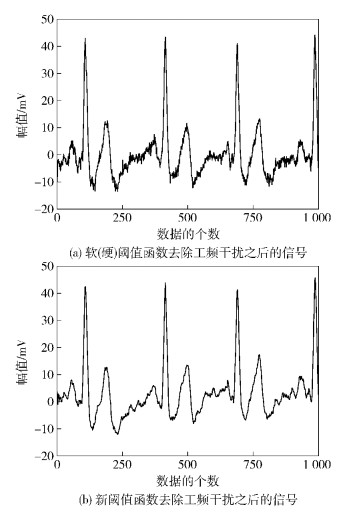
对第1、2、3尺度的高频系数用阈值函数和自适应阈值进行阈值处理可去除工频干扰,如图 2所示.
|
图 2 去除工频干扰对比图 |
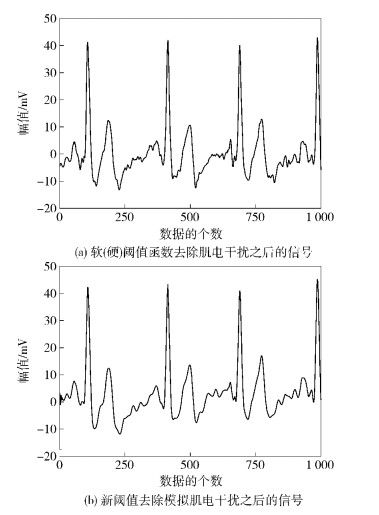
对第1、2、3、4、5尺度的高频系数用阈值函数和自适应阈值进行阈值处理可去除肌电干扰,如图 3所示.
|
图 3 去除模拟肌电干扰对比 |
从以上实验结果可以看出,平稳小波变换与新阈值函数相结合,可达到去除3种噪声的目的,比较完整地保留了原始心电信号中拐点、波峰等特征,与原始信号的幅度与精度保持一致,没有失真,几乎没有震荡,较好地抑制了伪吉布斯现象,没有边缘模糊现象,得到较好的去噪效果,有较高的SNR和较低的均方误差 (MSE,mean squared error).
数据的个数N=1 024时,新、软和硬阈值函数去噪后的SNR和MSE的比较如表 2所示.
|
|
表 2 3种阈值函数的去噪性能 |
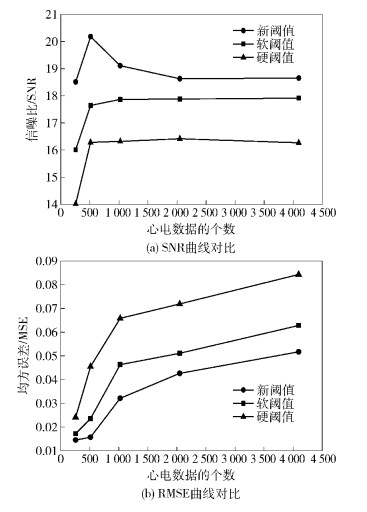
当数据的个数N分别取256、521、1 024、2 014、4 096时,分别用新、软和硬阈值函数进行去噪,得到各自的SNR和均方根误差 (RMSE,root mean squared error),并绘制出它们的对比曲线,如图 4所示.
|
图 4 新、软、硬阈值函数SNR和RMSE曲线对比 |
从图 4中可以看出,随着心电数据个数N的增加,3种阈值函数的SNR都有下降,RMSE都有所增加,但提出的新阈值函数的SNR高于常用的软硬阈值函数,RMSE低于常用的软硬阈值函数,更加验证提出算法的可行性.
4 结束语提出了一种基于平稳小波变换的新阈值去噪方法,选用bior5.5作为小波函数,对含噪的心电信号分别用硬阈值、软阈值和提出的新阈值法进行去噪.结果表明,提出的新阈值法的去噪效果是要优于另外2种的,即达到了消除噪声的目的,比较好地保留了原始心电信号的基本波形特征.
| [1] | Chaudhary M S, Kapoor R K, Sharma A K. Comparison between different wavelet transforms and thresholding techniques for ECG denoising[C]//Advances in Engineering and Technology Research (ICAETR), 2014 International Conference on. [S.l.]:IEEE, 2014:1-6. |
| [2] | Sui Wentao, Zhang Dan. Noise reduction of ECG using spatial correlation filtering and stationary wavelet transform[C]//Computer Science and Education (ICCSE), 2010 5th International Conference on. [S.l.]:IEEE, 2010:1085-1088. |
| [3] | Seena V, Yomas J. A review on feature extraction and denoising of ECG signal using wavelet transform[C]//Devices, Circuits and Systems (ICDCS), 2014 2nd International Conference on. [S.l.]:IEEE, 2014:1-6. |
| [4] | Lü Dan, Zhang Xin, Wang Yan, et al. The filtering of ECG signal based on variable length optimization method[J]. China Medical Device Information, 2009, 15(8): 36–38. |
| [5] | He Jun, Ma Youliang. ECG signal denoising wavelet function chosen quantitative research[J]. Information and Electronic Engineering, 2010, 8(3): 286–289. |


