2. 华北理工大学 研究生学院, 河北 唐山 063009
提出了一种基于傅氏级数的平面五杆机构计时轨迹综合的代数求解新方法。通过将平面五杆机构拆分为左右2个二杆组,对轨迹综合设计变量进行了解耦。在此基础上,分析得到机构尺寸与连杆曲线谐波参数间的函数关系,并依据这一关系建立了不同传动比条件下平面五杆机构轨迹综合设计方程,通过析配消元法进一步将方程化简为一元四次方程,求解得到了平面五杆机构轨迹综合设计参数计算的通用公式。利用该公式分别计算得到左右2个二杆组的设计参数,进而得到完整机构设计参数。给出了2个数值实例,验证了该方法的有效性和可行性。
2. Graduate School, North China University of Science and Technology, Hebei Tangshan 063009, China
A novel analytical approach is presented to solve path synthesis problems for planar five-bar linkages with timing. Firstly, the planar five-bar linkage is decomposed into two dyads for the purpose of decoupling the design parameters of the linkage. The relationship between the design parameters of the linkage and the harmonic parameters of the path is obtained, based on which, the new synthesis equations with different transmission ration for planar five-bar linkages are established. A quartic equation is obtained by dialytic elimination. As a result, a general formula is derived for calculation of the design parameters of a planar five-bar linkage. The design parameters of two dyads are obtained with the general formula respectively. At last, all design parameters of the planar five-bar linkage are obtained. Two numerical examples are provided to verify the effectiveness of the proposed algorithm.
平面五杆机构作为一种结构形式简单的并联机构,具有刚度大、承载能力强,可实现复杂轨迹的特点,在并联和混联机器人研究和设计中已获得应用[1].目前,对于该机构轨迹综合问题研究的主要方法包括代数法[2]、优化法[3-4]和数值图谱法[5-6].代数法具有精度高、重复性强等优点,但存在受机构未知参数的数目限制,无法实现多点轨迹综合的不足.优化法可实现多点位的连续轨迹综合,但其求解因受到初值选取、目标函数性态及寻优方法等因素的影响,有时难以得到稳定的全域最优解.数值图谱法具有解的多样性强、适用范围广的优点,但也存在完备图谱库建立难度大,求解精度低的缺点.在总结已有轨迹综合方法特点的基础上,提出一种基于傅氏级数的连杆机构轨迹综合的代数方法, 并利用这一方法对具有双曲柄的平面五杆机构计时轨迹综合问题进行了研究.与已有的代数方法不同,该方法不再是以位移矩阵或回路约束为基础,而是根据目标轨迹的谐波参数与机构尺寸间的关系建立综合方程,其不但可以完成多点位连续轨迹综合,而且通过方程求解得到综合结果,不需要提供优化的初值,也无需建立数据库.
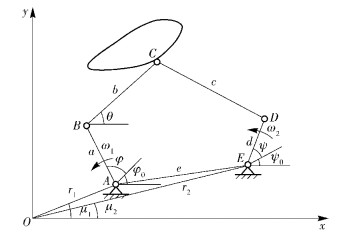
1 连杆曲线的傅氏级数表示图 1所示为平面五杆机构示意图,机构各杆长尺寸分别为a、b、c、d、e,φ、ψ分别为机构左右两输入曲柄转角,φ0、ψ0分别为两曲柄的初始相位角,ω1、ω2分别为两曲柄的转速,且有ω1:ω2=h1:h2(h1和h2为整数).
|
图 1 平面五杆机构轨迹生成图 |
平面五杆机构的连杆曲线为周期性封闭曲线,由文献[6]可知,当输入构件以匀速转动时,采用复矢量法描述连杆曲线,其可以表示为
| $ {\mathit{\boldsymbol{r}}_C}\left( t \right) = x\left( t \right) + {\rm{i}}y\left( t \right) $ | (1) |
其中:
| $ {\mathit{\boldsymbol{r}}_C}\left( t \right) = x\left( t \right) + {\rm{i}}y\left( t \right) = \sum\limits_{n = - \infty }^{ + \infty } {{c_n}{{\rm{e}}^{{\rm{i}}n\omega t}}} $ | (2) |
其中cn为机构连杆曲线傅氏级数展开的谐波参数,且有
| $ {c_n} = \frac{1}{{2\pi }}\int_0^{2\pi } {\left( {x\left( t \right) + {\rm{i}}y\left( t \right)} \right){{\rm{e}}^{{\rm{i}}n\omega t}}{\rm{d}}t} $ | (3) |
由于连杆曲线为复杂函数曲线,有时难以用显函数形式表达,常是以一系列离散点的形式给出,因此,cn更多时候需要通过数值计算方法得到.根据离散傅里叶变换的性质,可得到cn的离散数值解表达式
| $ {c_n} = \frac{1}{M}\sum\limits_{m = 0}^{M - 1} {\left( {{x_m} + {\rm{i}}{y_m}} \right)\left[ {\cos \left( {nm\omega } \right) - {\rm{i}}\sin \left( {nm\omega } \right)} \right]} $ | (4) |
其中:n=0, ±1, …, ±(M-1);m=0, ±1, …, ±(M-1),M为离散点个数,ω=±(2π/M)(输入曲柄逆时针旋转时取正, 顺时针旋转时取负,与传动比符号一致).
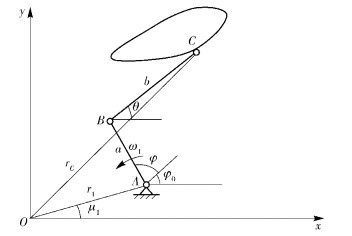
2 综合设计方程建立在连杆机构设计时,常用的简化设计方法是先将机构分解成若干二杆组,再分别计算不同二杆组的参数,进而得到完整机构设计参数.平面五杆机构可看成由两个二自由度开链机构CBA和CDE在铰链点C处组合而成,其可分解为两个铰链二杆组. 图 2所示为机构左侧二杆组,建立如图 2所示的坐标系.
|
图 2 平面五杆机构左侧二杆组示意图 |
应用矢量法分析左侧二杆组,可得矢量方程为
| $ {\mathit{\boldsymbol{r}}_1} + \mathit{\boldsymbol{a}} + \mathit{\boldsymbol{b}} = {\mathit{\boldsymbol{r}}_C} $ | (5) |
将方程 (5) 表示为复数矢量形式为
| $ {\mathit{\boldsymbol{r}}_C} - {\mathit{\boldsymbol{r}}_1}{e^{{\rm{i}}{\mu _1}}} - a{{\rm{e}}^{{\rm{i}}\left( {\varphi + {\varphi _0}} \right)}} = b{{\rm{e}}^{{\rm{i}}\theta }} $ | (6) |
取式 (6) 共轭可得
| $ {{\mathit{\boldsymbol{\bar r}}}_C} - {\mathit{r}_1}{e^{ - {\rm{i}}{\mu _1}}} - a{{\rm{e}}^{ - {\rm{i}}\left( {\varphi + {\varphi _0}} \right)}} = b{{\rm{e}}^{ - {\rm{i}}\theta }} $ | (7) |
将式 (6) 与式 (7) 相乘,化简可得
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{r}}_C}{{\mathit{\boldsymbol{\bar r}}}_C} - u{{\mathit{\boldsymbol{\bar r}}}_C} - x{{\mathit{\boldsymbol{\bar r}}}_C}{{\rm{e}}^{{\rm{i}}\varphi }} + yu{{\rm{e}}^{ - {\rm{i}}\varphi }} + w + }\\ {yu{{\rm{e}}^{{\rm{i}}\varphi }} - y{\mathit{\boldsymbol{r}}_C}{{\rm{e}}^{ - {\rm{i}}\varphi }} - v{\mathit{\boldsymbol{r}}_C} = 0} \end{array} $ | (8) |
其中:u=r1eiμ1,v=r1e-iμ1,x=aeiφ0,y=ae-iφ0,w=r12+a2-b2.
由式 (2) 可知,rC、rC展成傅氏级数为
| $ \begin{array}{l} {\mathit{\boldsymbol{r}}_C} = \sum\limits_{n = - \infty }^{ + \infty } {{c_n}{{\rm{e}}^{{\rm{i}}n\omega t}}} = {c_0} + {c_{ - 1}}{{\rm{e}}^{ - {\rm{i}}\omega t}} + {c_1}{{\rm{e}}^{{\rm{i}}\omega t}} + \\ {c_{ - 2}}{{\rm{e}}^{ - 2{\rm{i}}\omega t}} + {c_2}{{\rm{e}}^{2{\rm{i}}\omega t}} + \cdots + {c_{ - n}}{{\rm{e}}^{ - n{\rm{i}}\omega t}} + {c_n}{{\rm{e}}^{n{\rm{i}}\omega t}} \end{array} $ | (9) |
| $ \begin{array}{l} {{\mathit{\boldsymbol{\bar r}}}_C} = \sum\limits_{n = - \infty }^{ + \infty } {{{\bar c}_n}{{\rm{e}}^{ - {\rm{i}}n\omega t}}} = {{\bar c}_0} + {{\bar c}_{ - 1}}{{\rm{e}}^{{\rm{i}}\omega t}} + {{\bar c}_1}{{\rm{e}}^{ - {\rm{i}}\omega t}} + \\ {{\bar c}_{ - 2}}{{\rm{e}}^{2{\rm{i}}\omega t}} + {{\bar c}_2}{{\rm{e}}^{ - 2{\rm{i}}\omega t}} + \cdots + {{\bar c}_{ - n}}{{\rm{e}}^{n{\rm{i}}\omega t}} + {{\bar c}_n}{{\rm{e}}^{ - n{\rm{i}}\omega t}} \end{array} $ | (10) |
理论上,rC、rC应由无穷多项傅氏级数之和来表示,由文献[6]可知,实际设计中取有限项谐波就可满足设计要求,因此,可根据综合设计精度要求确定n的取值.将式 (9)、式 (10) 和φ=kωt代入式 (8),合并同类项整理可得
| $ \begin{array}{*{20}{c}} {{H_0} + {H_{ - 1}}{{\rm{e}}^{ - {\rm{i}}\omega t}} + {H_1}{{\rm{e}}^{{\rm{i}}\omega t}} + \cdots + {H_{ - k}}{{\rm{e}}^{ - k{\rm{i}}\omega t}} + }\\ {{H_k}{{\rm{e}}^{k{\rm{i}}\omega t}} + \cdots + {H_{ - j}}{{\rm{e}}^{ - n{\rm{i}}\omega t}} + {H_j}{{\rm{e}}^{n{\rm{i}}\omega t}} = 0} \end{array} $ | (11) |
其中
| $ \begin{array}{*{20}{c}} {{H_0} = u{{\bar c}_0} + u{{\bar c}_k} + y{c_k} + v{c_0} - w - {K_0}}\\ {{H_{ - k}} = u{{\bar c}_k} + x{{\bar c}_{2k}} + y{c_0} + v{c_{ - k}} - yu - {K_{ - k}}}\\ {{H_k} = u{{\bar c}_{ - k}} + x{{\bar c}_0} + y{c_{2k}} + v{c_k} - xv - {K_k}}\\ {{H_{ - j}} = u{{\bar c}_j} + x{{\bar c}_{k + j}} + y{c_{k - j}} + v{c_{ - j}} - {K_{ - j}}}\\ {{H_j} = u{{\bar c}_{ - j}} + x{{\bar c}_{k - j}} + y{c_{k + j}} + v{c_j} - {K_j}} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{K_{ - k}} = \sum\limits_{{m_1} = - \left( {n - k} \right)}^{n - k} {{c_{{m_1}}}{{\bar c}_{{m_1} + k}}} ,{K_k} = \sum\limits_{{m_1} = - \left( {n - k} \right)}^{n - k} {{c_{{m_1}}}{{\bar c}_{{m_1} - k}}} ,}\\ {k = \left| {{h_1}} \right|,{m_1} = 0, \pm 1, \cdots \pm k, \cdots , \pm \left( {n - k} \right),}\\ {{K_{ - j}} = \sum\limits_{{m_2} = - \left( {n - j} \right)}^{n - j} {{c_{{m_2}}}{{\bar c}_{{m_2} - j}}} ,{K_{ - j}} = \sum\limits_{{m_2} = - \left( {n - j} \right)}^{n - j} {{c_{{m_2}}}{{\bar c}_{{m_2} + j}}} ,}\\ {j = 0,1, \cdots ,n,j \ne k,}\\ {{m_2} = 0, \pm 1, \cdots \pm k, \cdots , \pm \left( {n - j} \right)} \end{array} $ |
分析可以发现,H-j、H-k、H0、Hk、Hj为含有机构参数和连杆曲线谐波参数的表达式,由复指数性质可知,其值应为0.由文献[7]可知,连杆曲线谐波参数的绝对值随着谐波次数的增加将不断减小,对曲线形状的影响逐渐减弱,因此取含有设计变量和低次谐波项表达式建立如下方程:
| $ {H_{ - k}} = u{{\bar c}_k} + x{{\bar c}_{2k}} + y{c_0} + v{c_{ - k}} - yu - {K_{ - k}} $ | (12a) |
| $ {H_{ - 1}} = u{{\bar c}_1} + x{{\bar c}_{k + 1}} + y{c_{k - 1}} + v{c_{ - 1}} - {K_{ - 1}} $ | (12b) |
| $ {H_0} = u{{\bar c}_0} + u{{\bar c}_k} + y{c_k} + v{c_0} - w - {K_0} $ | (12c) |
| $ {H_1} = u{{\bar c}_{ - 1}} + x{{\bar c}_{k - 1}} + y{c_{k + 1}} + v{c_1} - {K_1} $ | (12d) |
| $ {H_k} = u{{\bar c}_{ - k}} + x{{\bar c}_0} + y{c_{2k}} + v{c_k} - xv - {K_k} $ | (12e) |
式 (12) 即为机构轨迹综合的设计方程.其中x、y、u、v、w为含有设计参数的未知变量,cn、cn(n=0, ±1, …, ±2k) 为目标轨迹的谐波参数,可通过式 (4) 计算得到.采用析配消元法进一步化简方程,将方程 (12a)、(12b)、(12d)、(12e) 乘以u后与原方程一起构成多项式方程组,写成矩阵形式为
| $ \mathit{\boldsymbol{DX = }}0 $ | (13) |
式 (13) 可看作一个含有8个未知量的线性方程组,未知量为X=[1, u, y, v, yu, u2, uv, yu2]T,D为一个8×8阶的系数矩阵:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{D}} = }\\ {\left[ {\begin{array}{*{20}{c}} {x{{\bar c}_{2k}} - {K_{ - k}}} & {{{\bar c}_k}} & {{c_0}} & {{c_{ - k}}} & { - 1} & 0 & 0 & 0\\ {x{{\bar c}_{k + 1}} - {K_{ - 1}}} & {{{\bar c}_1}} & {{c_{k - 1}}} & {{c_{ - 1}}} & 0 & 0 & 0 & 0\\ {x{{\bar c}_{k - 1}} - {K_1}} & {{{\bar c}_{ - 1}}} & {{c_{k + 1}}} & {{c_1}} & 0 & 0 & 0 & 0\\ {x{{\bar c}_0} - {K_k}} & {{{\bar c}_{ - k}}} & {{c_{2k}}} & {{c_k} - x} & 0 & 0 & 0 & 0\\ 0 & {x{{\bar c}_{2k}} - {K_{ - k}}} & 0 & 0 & {{c_0}} & {{{\bar c}_k}} & {{c_{ - k}}} & { - 1}\\ 0 & {x{{\bar c}_{k + 1}} - {K_{ - 1}}} & 0 & 0 & {{c_{k - 1}}} & {{{\bar c}_1}} & {{c_{ - 1}}} & 0\\ 0 & {x{{\bar c}_{k - 1}} - {K_1}} & 0 & 0 & {{c_{k + 1}}} & {{{\bar c}_{ - 1}}} & {{c_1}} & 0\\ 0 & {x{{\bar c}_0} - {K_k}} & 0 & 0 & {{c_{2k}}} & {{{\bar c}_{ - k}}} & {{c_k} - x} & 0 \end{array}} \right]} \end{array} $ |
由代数学知识可知,方程组 (13) 有解的条件是其系数行列式等于0,即
| $ \left| \mathit{\boldsymbol{D}} \right|\mathit{\boldsymbol{ = }}0 $ | (14) |
将式 (14) 展开可得到含有x的一元四次方程:
| $ {p_4}{x^4} + {p_3}{x^3} + {p_2}{x^2} + {p_1}x + {p_0} = 0 $ | (15) |
其中pi(i=1, 2, 3, 4) 是由目标轨迹谐波参数cn、cn构成的已知量.求解方程 (15) 可得到x的4个非零解析解,将所得x解代入式 (13) 可得到y、u、v的解,再将所得x、y、u、v的解代入式 (12c) 可得到对应w解.求得x、y、u、v、w解后,可由下列公式得到r1、a、b、μ1、φ0的解.
| $ \begin{array}{*{20}{c}} {{r_1} = \pm \sqrt {uv} ,a = \pm \sqrt {xy} ,b = \pm \sqrt {xy + uv - w} ,}\\ {{\mu _1} = - {\rm{i}}\ln \frac{u}{{{r_1}}},{\varphi _0} = - {\rm{i}}\ln \frac{x}{a}} \end{array} $ |
进一步分析可知,r1、a、b、μ1、φ0的解可转化为仅含有cn、cn的计算公式,将其称为平面五杆机构轨迹综合设计参数计算的通用公式.需要注意的是,当k=1时,方程 (12b) 和 (12d) 将不再成立,方程组 (12) 减少为3个方程,此时可将H2、H-2添加到方程组中构成综合设计方程.由于右侧二杆组结构与左侧相同,将对应参数进行代换,采用上述方法同样可计算得到右侧二杆组设计参数,再将两者结合起来就可得到平面五杆机构轨迹综合的全部设计参数.
3 综合步骤依据前面的分析,可以建立平面五杆机构轨迹综合的代数方法.
1) 根据两输入曲柄不同传动比,利用式 (4) 对目标轨迹进行离散傅里叶变换,计算得到左右两侧二杆组对应目标轨迹的谐波参数cn.
2) 将所得的谐波参数cn代入平面五杆机构轨迹综合通用公式,计算得到左右两侧二杆组的设计参数.
3) 分别选取左、右两侧二杆组的一组设计参数,组成平面五杆机构,对所得机构进行运动分析,检验其是否存在曲柄,有无分支问题、顺序问题,最终得到满足设计要求的平面五杆机构.
4 综合实例例1 综合平面五杆机构,使其在传动比为1的条件下近似实现方程为
1) 计算得到目标轨迹的谐波参数cn,传动比为1时,两侧二杆组的对应谐波参数相同,表 1所示为目标轨迹的-4到4次谐波参数值.
|
|
表 1 目标轨迹的谐波参数 |
2) 将所得谐波参数代入平面五杆机构轨迹综合设计参数计算通用公式,计算得到左右两侧二杆组的设计参数,传动比为1时,计算所得两侧二杆组的设计参数相同,表 2所示为4组有意义的实数解.
|
|
表 2 计算所得二杆组的设计参数 |
3) 任选上述两组参数可组成一个完整平面五杆机构,应用仿真程序进行运动分析检验,得到满足设计要求的机构参数如下
| $ \begin{array}{l} {r_1} = 81.{\rm{ }}921{\rm{ }}9,{r_2} = 61.678{\rm{ }}5,a = 2.997{\rm{ }}6,b = 79.822{\rm{ }}7\\ c = 66.120{\rm{ }}4,d = 2.352{\rm{ }}8,{\mu _1} = 3.092{\rm{ }}8,{\mu _2} = - 0.974{\rm{ }}3,\\ {\varphi _0} = 0.004{\rm{ }}9,{\psi _0} = {\rm{ }} - 0.201{\rm{ }}4 \end{array} $ |
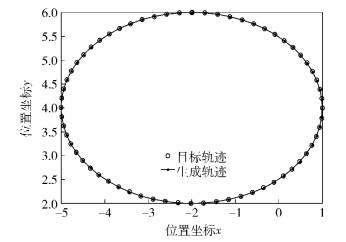
图 3所示为目标轨迹与综合机构生成轨迹的比较,从图中可以发现,该方法综合得到的机构能够较好地再现目标轨迹.
|
图 3 目标轨迹与综合机构生成轨迹比较 |
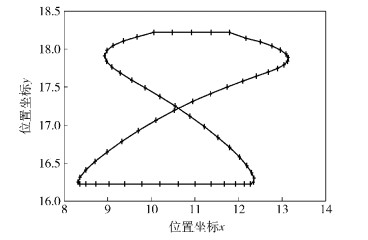
例2 图 4所示为一条8字形轨迹,且其上下部分各包含一水平直线段,综合平面五杆机构,使其在传动比为ω1:ω2=1:-2的条件下近似实现该目标轨迹.
|
图 4 目标轨迹 |
综合步骤与例1的相同,表 3、表 4为计算得到左右两侧二杆组对应目标轨迹的谐波参数和设计参数,分别在左右两侧二杆组中各选取一组设计参数,组成平面五杆机构,可得到16个综合机构.
|
|
表 3 目标轨迹的谐波参数 |
|
|
表 4 计算所得左右两侧二杆组的设计参数 |
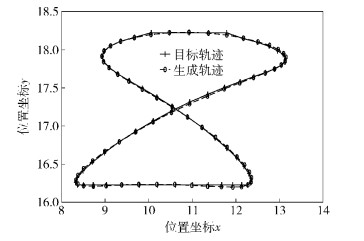
通过仿真程序对综合所得机构进行运动分析,发现左右两侧均取第3组参数时组成的平面五杆机构生成轨迹与目标轨迹最为接近,且不存在分支和逆序问题,满足设计要求. 图 5所示为目标轨迹与机构生成轨迹的比较.
|
图 5 目标轨迹与综合机构生成轨迹比较 |
建立了一种基于傅氏级数的平面五杆机构轨迹综合代数求解新方法.通过将平面五杆机构分解为两个二杆组,对轨迹综合设计变量进行解耦.在此基础上,分析得到机构尺寸与连杆曲线谐波参数间的函数关系,依据这一关系建立了不同传动比条件下平面五杆机构轨迹综合设计的新方程,通过配析消元法进一步将方程化简为一元四次代数方程,得到了平面五杆机构轨迹综合设计参数计算的通用公式.与已有的综合方法相比,该方法在实现多点轨迹综合的同时,采用解析方法求解,无需给定初值和建立数值图谱库,具有求解精度高,计算速度快,便于计算机编程的特点;同时,其可得出多组可行方案,为机构的进一步筛选和优化提供了前提.
| [1] | 辛洪兵, 余跃庆. 平面五杆并联机器人运动学导论[M]. 北京: 国防工业出版社, 2007. |
| [2] | Starns G, Flugrad D R. Five-bar path generation synthesis by continuation methods[J]. Journal of Mechanical Design, 1993, 115(4): 988–994. doi: 10.1115/1.2919297 |
| [3] | Bus'kiewicz J. Use of shape invariants in optimal synthesis of geared five-bar linkage[J]. Mechanism and Machine Theory, 2010, 45(2): 273–290. doi: 10.1016/j.mechmachtheory.2009.09.004 |
| [4] | Lin Wenyi. Optimum path synthesis of a geared five-bar mechanism[J]. Advances in Mechanical Engineering, 2013(2): 1–13. |
| [5] | Chu Jinkui, Sun Jianwei. Numerical atlas method for path generation of spherical four-bar mechanism[J]. Mechanism and Machine Theory, 2010, 45(6): 867–879. doi: 10.1016/j.mechmachtheory.2009.12.005 |
| [6] | 褚金奎, 孙建伟. 连杆机构尺度综合的谐波特征参数法[M]. 北京: 科学出版社, 2010. |
| [7] | McGarva J, Mullineux G. Harmonic representation of closed curves[J]. Applied Mathematical Modelling, 1993, 17(4): 213–218. doi: 10.1016/0307-904X(93)90109-T |


